Modeling Spatial Context in ClassificationPrediction Using MRF and

Outline n n n n Introduction Problem Definition Supervised Classification Spatial Context Markov Random

Introduction n Spatial Databases n n n Objectives n n n Maps, Ground Observations,

Problem Definition n Given n n Find n n Classification model: f^L : R

Problem Definition n n Given n Multi-spectral image X, composed of N-dimensional Pixels n

Classical Techniques n Logistic Regression n n Assumptions n n n y=X + independent,

Pixel Classification n n Class to which a pixel at location x belongs it

Comparison Criteria Logistic Regression Bayesian Input fx 1, …, fxk, fl Intermediate Results Pr(li),

Spatial Context n What is spatial context? n n n Observations at location i

Prior Distribution Model: n For Markov random field , the conditional distribution of a

MRF Continued n A Clique is defined as a subset of points in S

Gibbs Distribution n For a given neighborhood system, a Gibbs distribution is defined as

Hammersley-Clifford Theorem n H-C theorem states that is an MRF with strictly positive distribution

ICM n 1. Compute 2. For all pixels (i, j), update 3. Repeat 2.

SAR n y= Wy+X + n n W is the contiguity matrix strength of

Experimental Results n Experimental Setup

Conclusion n n n Comparison on a common probabilistic framework. Modeling spatial dependencies SAR

Slides: 29

Download presentation

Modeling Spatial Context in Classification/Prediction Using MRF and SAR techniques. Shashi Shekhar Weili Wu Sanjay Chawla Ranga Raju Vatsavai Department of Computer Science. Army HPC Research Center. University of Minnesota.

Outline n n n n Introduction Problem Definition Supervised Classification Spatial Context Markov Random Fields (MRF) Spatial Autoregression (SAR) Results

Introduction n Spatial Databases n n n Objectives n n n Maps, Ground Observations, Multi-spectral/Multi-temporal remote sensing images e. g. Ecology (Wetlands), Forest Inventory, Aerial Photographs and Satellite Remote Sensing images Predict spatial distribution of marsh-breeding birds Thematic Classification – identification of objects in a imagery Techniques n n n Supervised, Unsupervised Statistical, Neural Knowledge Based

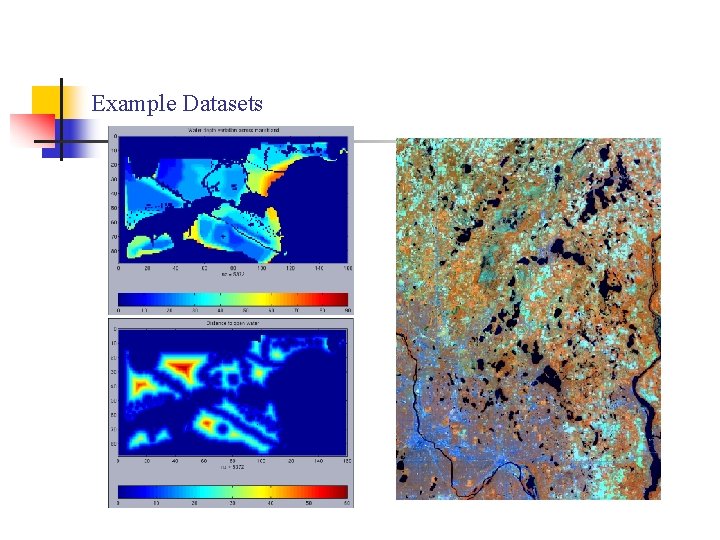
Example Datasets

Problem Definition n Given n n Find n n Classification model: f^L : R 1 x …RK –> L. Objective n n A spatial framework S consisting of {s 1, …, sn} for an underlying geographic space G A collection of explanatory functions f. Xk : S -> Rk, k = 1, …, K. Rk is the range A dependent class variable f. L : S -> L = {l 1, …, l. M} A value for parameter , relative importance of spatial accuracy Maximize similarity ( = (1 - )classification_acc(f^L , f. L ) + ( )spatial_acc(f^L , f. L )) Constraints n n S is multi-dimensional Euclidean space Explanatory functions and response function may not be independent, i. e. spatial autocorrelation exists.

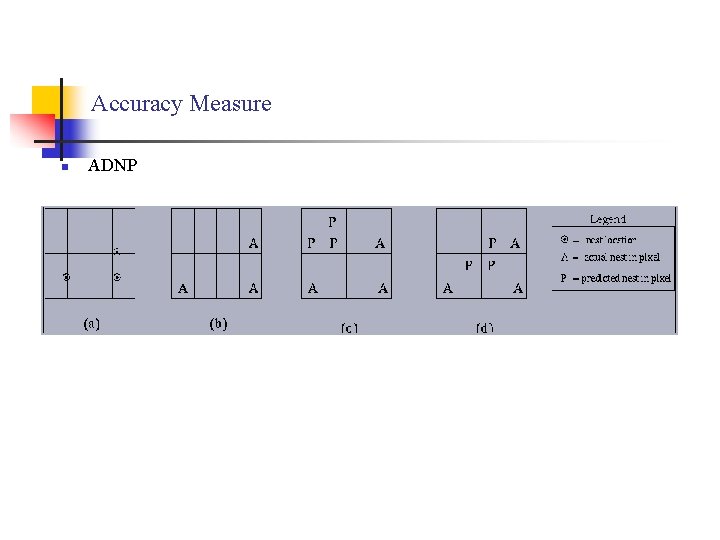
Accuracy Measure n ADNP

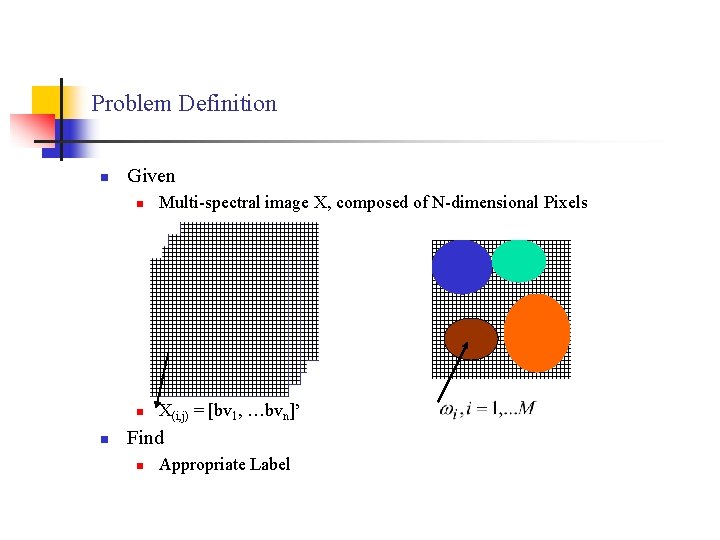
Problem Definition n n Given n Multi-spectral image X, composed of N-dimensional Pixels n X(i, j) = [bv 1, …bvn]’ Find n Appropriate Label

Classical Techniques n Logistic Regression n n Assumptions n n n y=X + independent, identical, zero-mean, normal distribution i. e. i = N ( 0, 2 ). Bayesian Classification n Pr(li | X) = Pr(X | li) Pr(li) / Pr(X).

Classification Schemes

Pixel Classification n n Class to which a pixel at location x belongs it is strictly the conditional probability Decision Rule

Classification

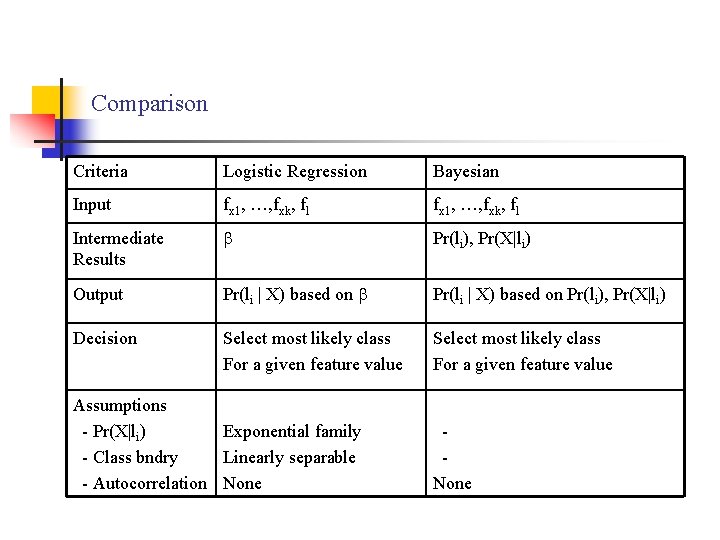
Comparison Criteria Logistic Regression Bayesian Input fx 1, …, fxk, fl Intermediate Results Pr(li), Pr(X|li) Output Pr(li | X) based on Pr(li), Pr(X|li) Decision Select most likely class For a given feature value Assumptions - Pr(X|li) Exponential family - Class bndry Linearly separable - Autocorrelation None

Spatial Context n What is spatial context? n n n Observations at location i depend on observations at location j Formally yi = f(yj), j = 1, 2, …. . n j i. Why? n n Natural Objects (Species) occur together Higher sensor resolution (i. e. object is bigger than pixel). i.

Prior Distribution Model: n For Markov random field , the conditional distribution of a point in the field given all other points is only dependent on its neighbors. x x s x x x x s x x x x

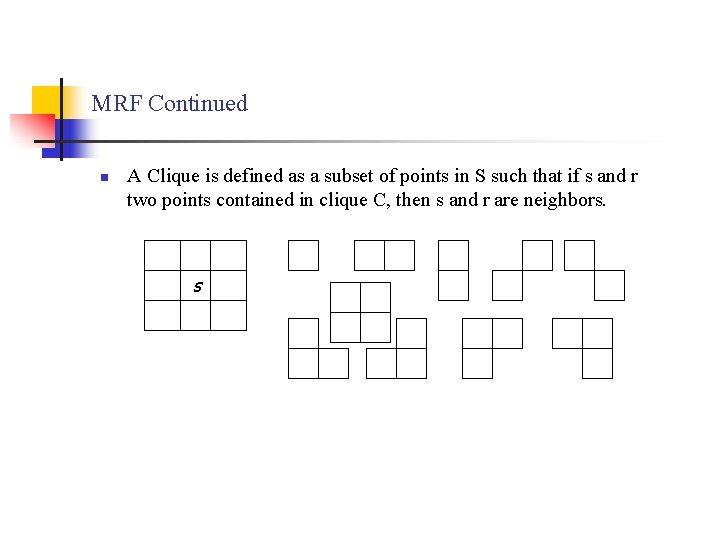
MRF Continued n A Clique is defined as a subset of points in S such that if s and r two points contained in clique C, then s and r are neighbors. s

Gibbs Distribution n For a given neighborhood system, a Gibbs distribution is defined as any distribution expressed as:

Hammersley-Clifford Theorem n H-C theorem states that is an MRF with strictly positive distribution and a neighborhood system the distribution of can be written as a Gibbs distribution with cliques induced by the neighborhood system. Therefore, if p( ) is formulated as Gibbs distribution, would have properties of MRF.

Gibbs Distribution

ICM n 1. Compute 2. For all pixels (i, j), update 3. Repeat 2. n Assuming multivariate normal distribution: n n n

SAR n y= Wy+X + n n W is the contiguity matrix strength of spatial dependencies

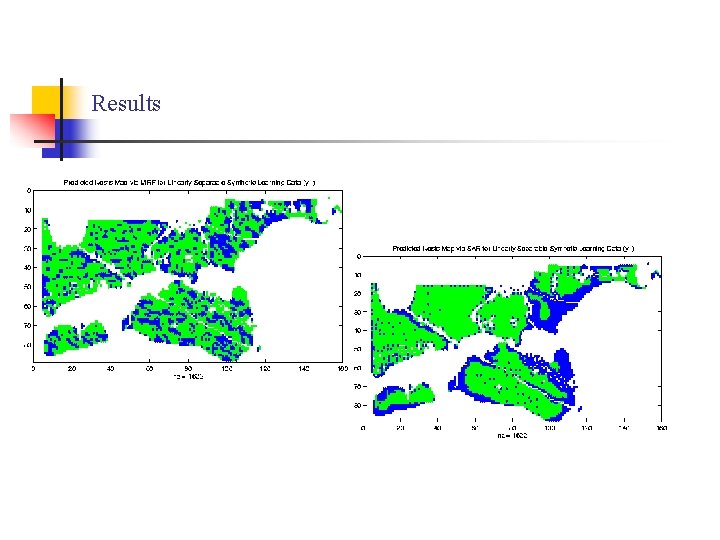
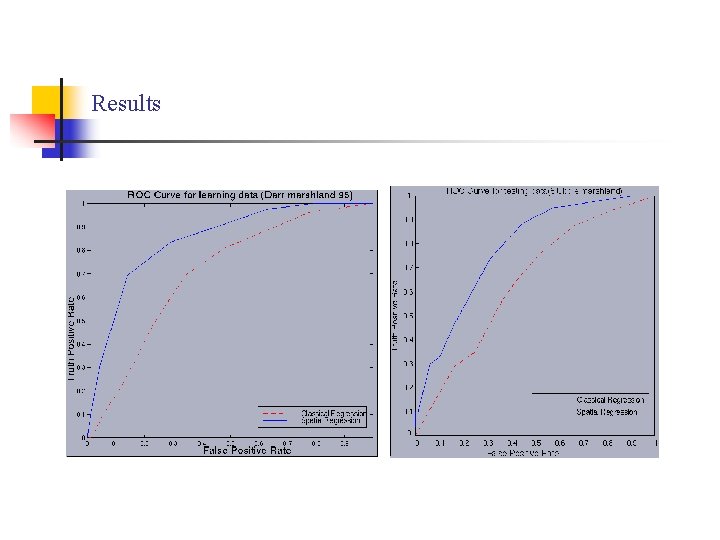
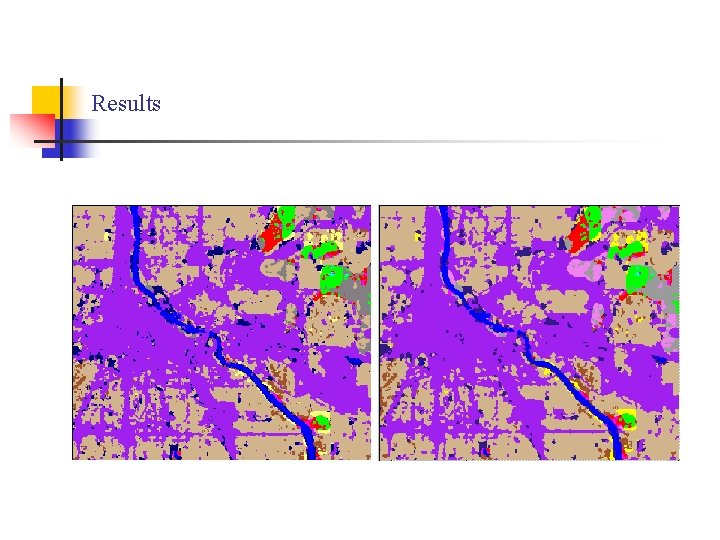
Experimental Results n Experimental Setup

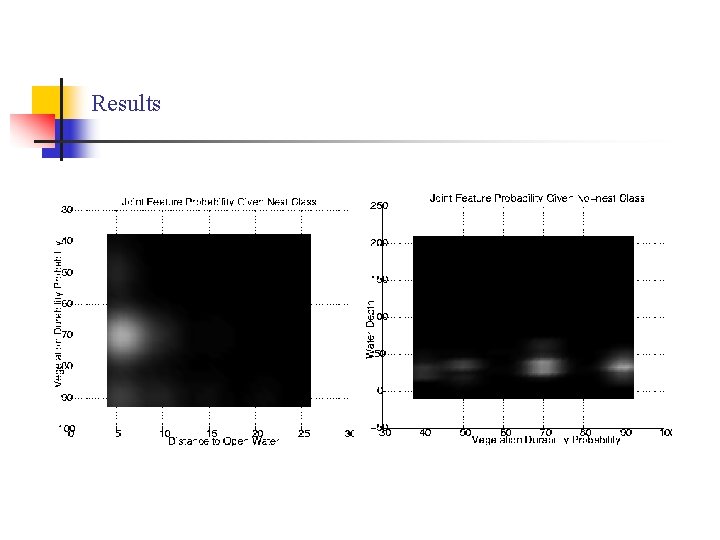
Results

Conclusion n n n Comparison on a common probabilistic framework. Modeling spatial dependencies SAR makes more restrictive assumptions than MRF allows flexible modeling of spatial context Relationship between SAR and MRF is analogues to logistic regression and Bayesian classifiers. Efficient Solution procedures n n Graph-cut Extend the graph-cut to SAR.