Modeling Robot with n total limbs n1 limbs
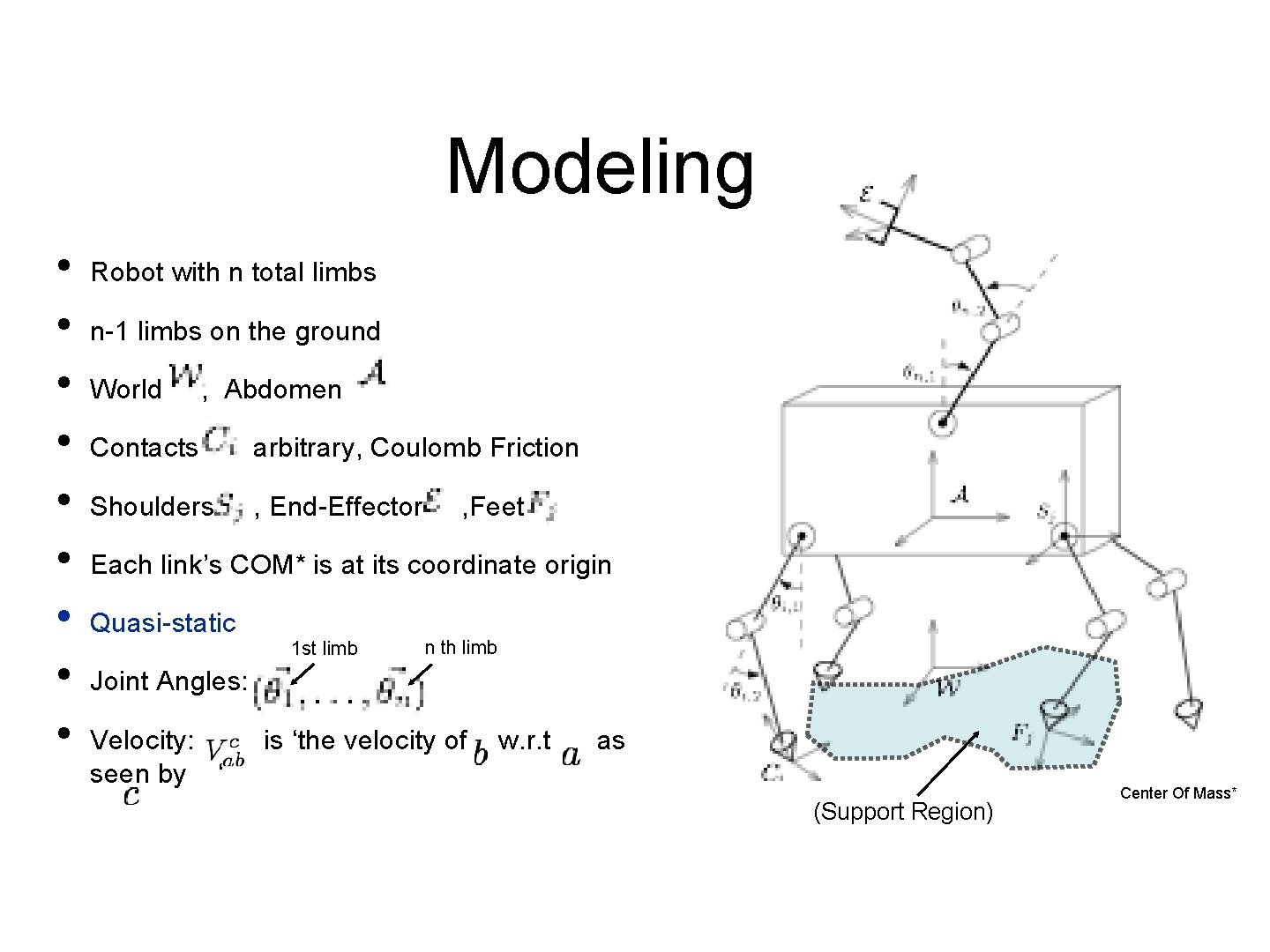
Modeling • • • Robot with n total limbs n-1 limbs on the ground World , Abdomen Contacts arbitrary, Coulomb Friction Shoulders , End-Effector , Feet Each link’s COM* is at its coordinate origin Quasi-static 1 st limb n th limb Joint Angles: Velocity: is ‘the velocity of w. r. t as seen by ‘ (Support Region) Center Of Mass*
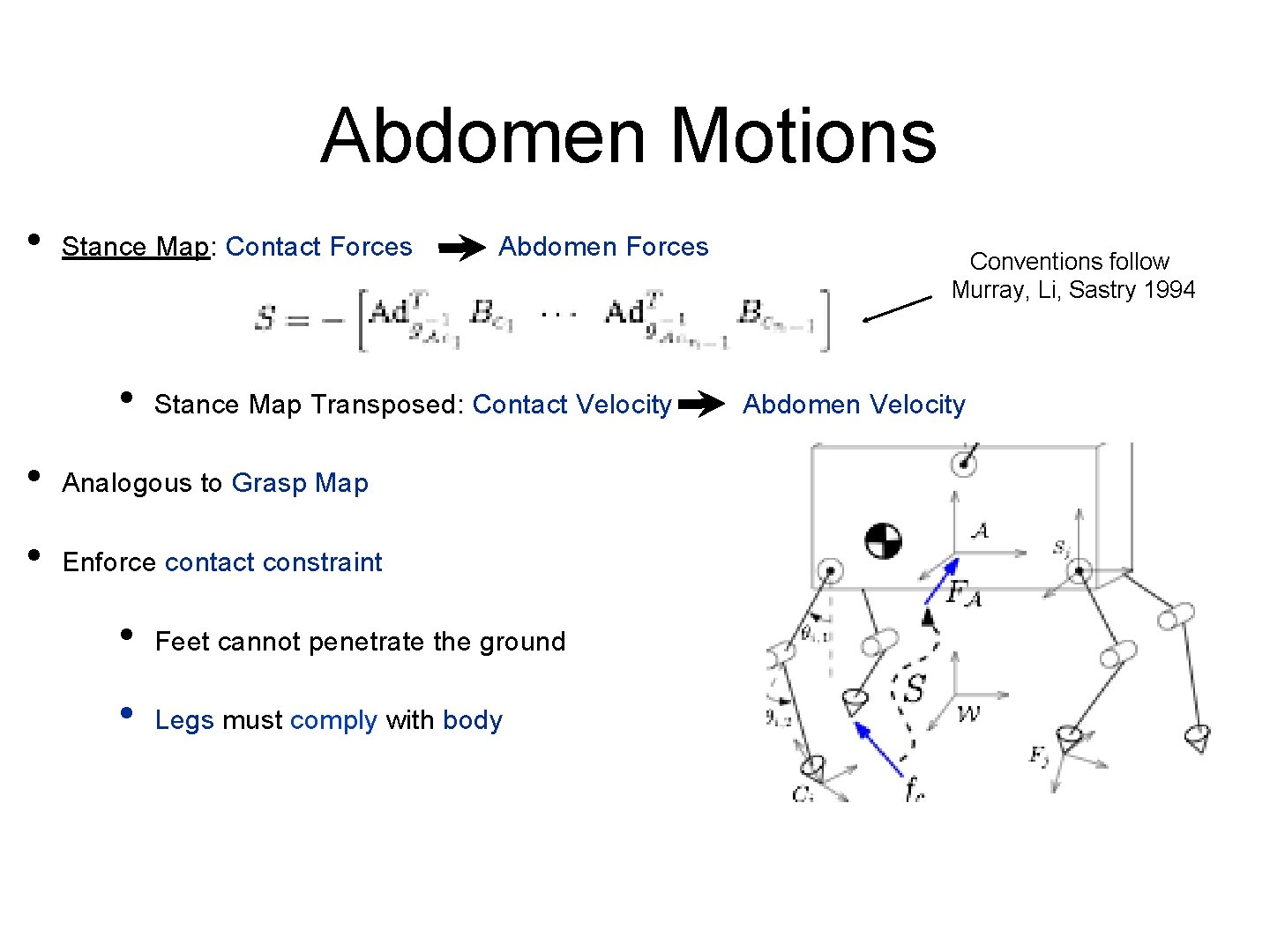
Abdomen Motions • Stance Map: Contact Forces Abdomen Forces • Conventions follow Murray, Li, Sastry 1994 Stance Map Transposed: Contact Velocity Abdomen Velocity • Analogous to Grasp Map • Enforce contact constraint • Feet cannot penetrate the ground • Legs must comply with body
Abdomen Velocity • Stance Jacobian: Joint Velocities Abdomen Velocities (contact information) • Analogous to Hand Jacobian
Free Limb Motions • Reach Jacobian: Joint velocities end-effector velocities • 2 Pieces: Free Limb w. rt world = (Abdomen Motion w. r. t world) + (Free Limb Motion w. r. t Abdomen)
![Analogies to Manipulation Similarity previously noted by many, e. g. [Waldron 1986], [Kumar and](http://slidetodoc.com/presentation_image_h/37cb420560fb760546c3c0a73d650104/image-5.jpg "Analogies to Manipulation Similarity previously noted by many, e. g. [Waldron 1986], [Kumar and")
Analogies to Manipulation Similarity previously noted by many, e. g. [Waldron 1986], [Kumar and Waldron 1987], [Hauser et al 2008], [Bretl and Lall 2008], [Johnson and Koditschek 2012]. Stance Kinematics make analogy explicit. Multi-Legged Robot Kinematics Stance Jacobian Stance Map Multi-Fingered Hand Kinematics* Hand Jacobian Grasp Manipulable Grasp Force Closure *Introduced by [Kerr, 1984] and [Salisbury, 1982]
Center of Mass Velocity • • Differentiate mass weighted average of link positions to get Stance Constrained Center of Mass Jacobian: Where (Weighted Jacobians)
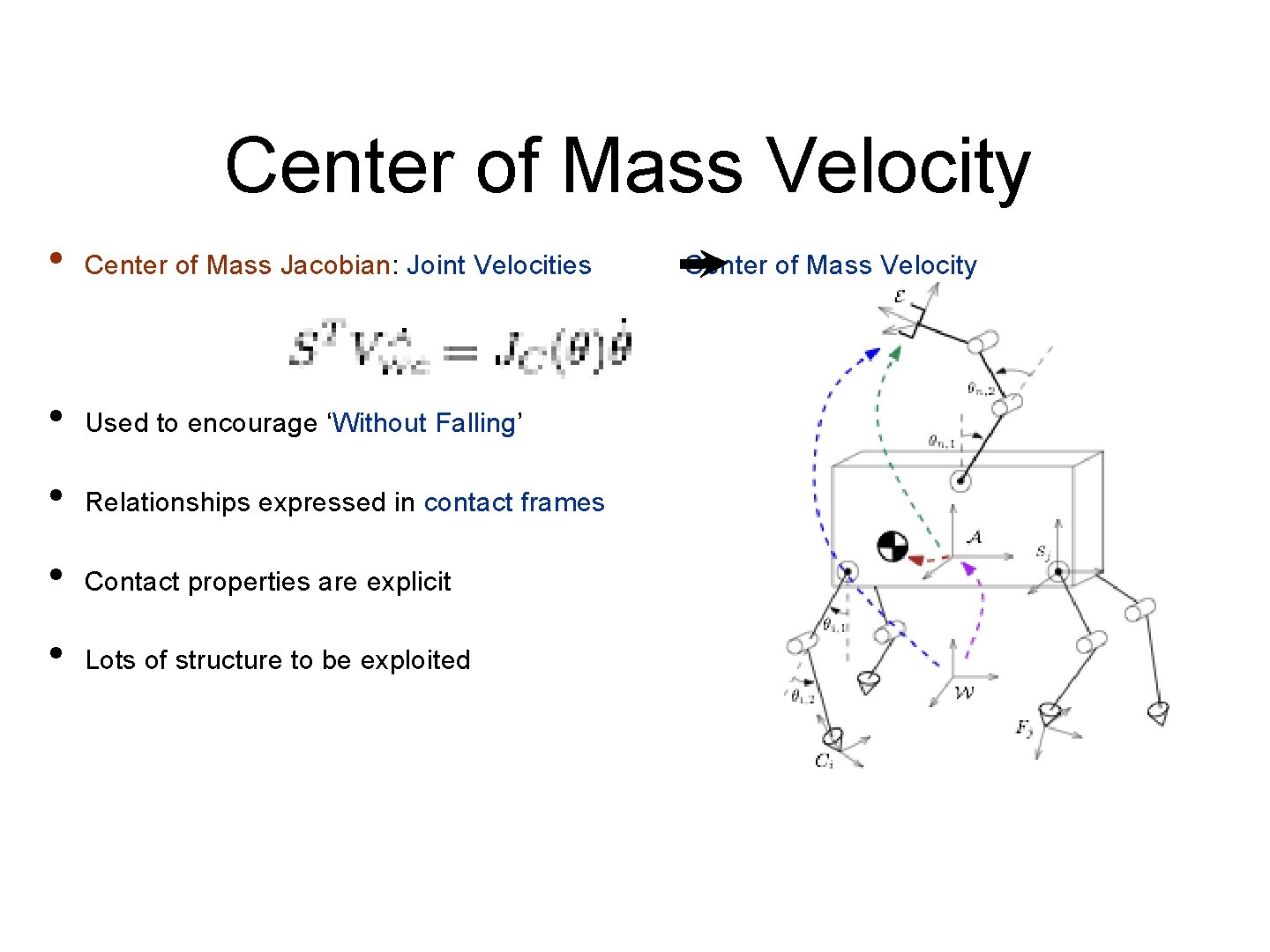
Center of Mass Velocity • Center of Mass Jacobian: Joint Velocities Center of Mass Velocity • Used to encourage ‘Without Falling’ • Relationships expressed in contact frames • Contact properties are explicit • Lots of structure to be exploited
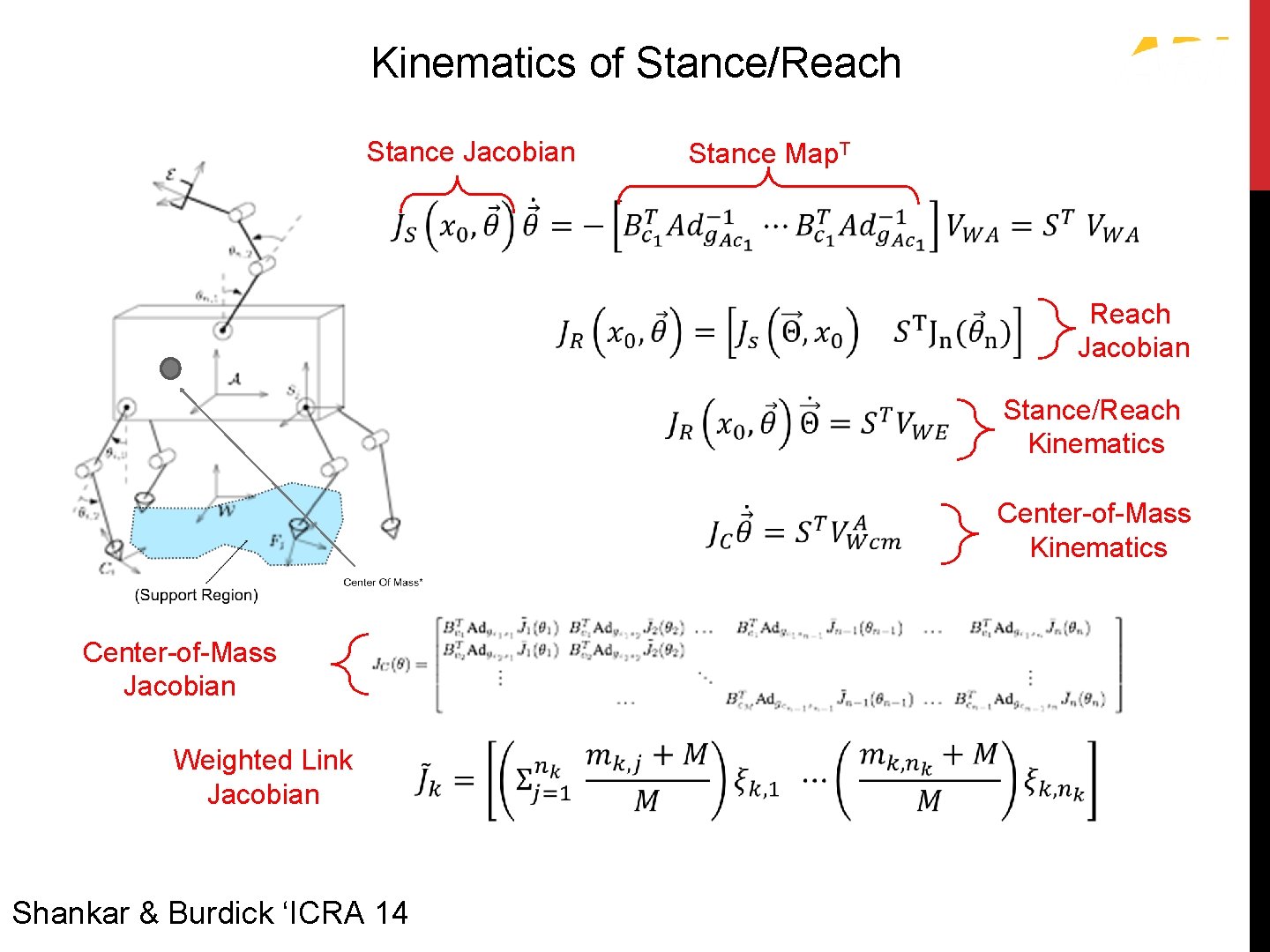
Kinematics of Stance/Reach Stance Jacobian Stance Map. T Reach Jacobian Center-of-Mass Jacobian Weighted Link Jacobian Shankar & Burdick ‘ICRA 14 Stance/Reach Kinematics Center-of-Mass Kinematics
![“Balanced Priority” Solution “Balanced Priority” Planning 1. Existence & Uniqueness results [ICRA’ 14] 2.](http://slidetodoc.com/presentation_image_h/37cb420560fb760546c3c0a73d650104/image-9.jpg "“Balanced Priority” Solution “Balanced Priority” Planning 1. Existence & Uniqueness results [ICRA’ 14] 2.")
“Balanced Priority” Solution “Balanced Priority” Planning 1. Existence & Uniqueness results [ICRA’ 14] 2. Closed form solution [IJRR’ 15] Extends to these geometries Shankar & Burdick ‘ICRA 14, IJRR’ 15
Efficient QP Formulation Quadratic Programming (QP) Linear feasibility Prog. Subject to Sub. to A LOT of constraints can be immediately incorporated (t = 1 if soln. exists, t = 0 otherwise) • Self-Collision Constraints (Bullet) • Hard Boundaries on Link motion • Point link in constant direction (gaze constraint) • Configuration Biasing (preferred walking pose) • Static Equilibrium Constraint • L 1 norm—release min number of joint breaks CVXGEN (Mattingley and Boyd) --(http: //www. cvxgen. com) • Custom solver runs extremely fast • 160 -320 microseconds for SURROGATE (21 DOF) • 220 -480 microseconds for Robo. Simian (28 DOF)
Efficient QP Formulation Quadratic Programming (QP) Linear Constraint Relax. Subject to Sub. to A LOT of constraints can be immediately incorporated • Self-Collision Constraints (Bullet) • Hard Boundaries on Link motion • Point link in constant direction (gaze constraint) • Configuration Biasing (preferred walking pose) • Static Equilibrium Constraint • L 1 norm—release min number of joint breaks CVXGEN (Mattingley and Boyd) --(http: //www. cvxgen. com) • Custom solver runs extremely fast • 160 -320 microseconds for SURROGATE (21 DOF) • 220 -480 microseconds for Robo. Simian (28 DOF)
Stance Jacobian
Reach Jacobian
Center of Mass Jacobian
- Slides: 14