Modeling Quantities Goal to establish a consistent method

Modeling Quantities • Goal – to establish a consistent method for representing physical quantities • Why? – easier for newcomers to understand – common software solution for handling common problems • units transformations • quantity combinations (math, units propagation, error prop…. ) – establish a base data model component that can be used to build up more complex objects.

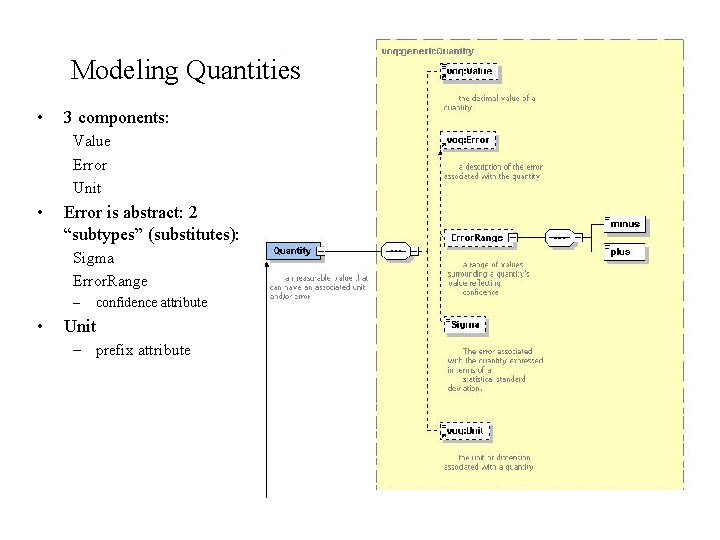
Modeling Quantities • 3 components: Value Error Unit • Error is abstract: 2 “subtypes” (substitutes): Sigma Error. Range – • confidence attribute Unit – prefix attribute

Modeling Quantities • Specific Quantities – substitutable for Quantity – restrict the unit Flux: Jy Length: m, pc, lt-yr Frequency: Hz, cm, e. V

<? xml version="1. 0" encoding="UTF-8"? > <Quantities xmlns="http: //www. ivoa. net/xml/prop/VOQuantity” xmlns: xsi="http: //www. w 3. org/2001/XMLSchema-instance"> <Quantity> <Value>44. 2</Value> <Sigma>0. 1</Sigma> <Unit prefix="k">m/s</Unit> </Quantity> <Length> <Value>4. 5</Value> <Unit prefix="M">pc</Unit> </Length> <Flux> <Value>18. 4</Value> <Error. Range confidence="67"> <minus>4. 1</minus> <plus>2. 4</plus> </Error. Range> <Unit prefix="m">Jy</Unit> </Flux> <Frequency> <Value>21</Value> <Unit prefix="c">m</Unit> </Frequency> </Quantities>

<? xml version="1. 0" encoding="UTF-8"? > <Quantities xmlns="http: //www. ivoa. net/xml/prop/VOQuantity" xmlns: xsi="http: //www. w 3. org/2001/XMLSchema-instance"> <Quantity> <Value>44. 2</Value> <Sigma>0. 1</Sigma> <Unit prefix="k">m/s</Unit> </Quantity> <Length> <Value>4. 5</Value> <Unit prefix="M">pc</Unit> </Length> <Flux> <Value>18. 4</Value> <Error. Range confidence="67"> <minus>4. 1</minus> <plus>2. 4</plus> </Error. Range> <Unit prefix="m">Jy</Unit> </Flux> <Frequency> <Value>21</Value> <Unit prefix="c">m</Unit> </Frequency> </Quantities> Alternatives: <Frequency p="c" u="m">21</Frequency> <Frequency>21 cm</Frequency> <Frequency value="21 cm"/> <Frequency p="c" u="m" sigma="0. 1" minus="0. 3" plus="0. 4" conf="99. 7">21</Frequency>

Modeling Quantities: Challenges • Quantity transformations – unit conversions * metric scaling * base unit (e. g. m Hz e. V) – parsing from human readable form ‘ 5 Jy’ is more compact and convenient but harder to parse • Comparisons & Processing Useful Functions: boolean near(q 1, q 2, tolerance) boolean within. Error(q 1, q 2) boolean less. Than(q 1, q 2) boolean greater. Than(q 1, q 2) Quantity to. Quantity(string) e. g. to. Quantity(‘ 5 Jy’) enables: greater. Than(Flux, ‘ 5 Jy’)