Modeling of Compressible Multiphase Flow through Porous Elastic

Modeling of Compressible Multiphase Flow through Porous Elastic Medium Yu. V. Perepechko*, E. I. Romenski†, G. V. Reshetova‡ *Institute of Geology & Mineralogy SB RAS †Institute of Mathematics SB RAS ‡Institute of Computational Mathematics & Mathematical Geophysics SB RAS

Introduction � Motivation: Modelling of multiphase flow in elastic porous media is a topical area of research in the general study of fluid flow regimes in petroleum reservoirs. The deep understanding of the coupled problem for multiphase mixture flow and finite elastoplastic deformation of a skeleton is very important for the development of new technologies of intensifying oil extracting. Despite the intensive research efforts there is still no a common approach and conventional mathematical model for the description of above mentioned processes. � Goal of the present research is to propose a new computational model for the multiphase flow in elastically deforming porous media in case of finite deformation of skeleton. The derivation of the model is based on thermodynamically compatible hyperbolic systems of conservation laws theory (Godunov and Romenskii 2003) and irreversible thermodynamics. � Results include derivation of new governing equations for the flow of compressible liquids mixture in elastic porous medium and high accuracy Runge-Kutta-WENO numerical method for solving differential equations of the model. The equations of the model comprise balance laws for phase masses, total momentum and total energy conservation laws supplemented by the equations for relative velocities and for deformation gradient in divergent form. The Runge-Kutta-WENO method up to 4 th order in time and 5 th order in space is developed for two-dimensional equations. 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Theory I. Parameters of state of the medium � � � is the volume fraction of elastic skeleton (phase 1) is the volume fractions of the fluids (n=2, …, N) is the mass density of the phase saturation constraints � is the total mass density of the medium � is the mass fraction of phase � is the velocity vector of phase i (i=1, 2, 3) is the relative velocity of phase with respect to the elastic porous phase is the mixture velocity of the medium � � � porosity is the deformation gradient of the whole medium is the entropy for the whole medium 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Theory I. The mixture energy � The mixture internal energy � The mixture full energy � First and second principle of thermodynamics 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Theory II. The master equations � The set of the master equations Godunov, S. K. and Romenskii, E. I. Elements of continuum mechanics and conservation laws. Kluwer Academic/Plenum Publ. , NY. 2003. 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Theory II. Governing Equations dissipative free thermodynamically compatible model � - total mass conservation � - phase mass fraction balance � - phase mass conservation � - relative velocities equation � - mixture momentum conservation � - deformation gradient conservation 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Theory II. Governing Equations dissipative thermodynamically compatible model � - total mass conservation � - phase mass fraction balance � - phase mass conservation � - relative velocities equation � - mixture momentum conservation � - deformation gradient conservation 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Theory II. Governing Equations dissipative thermodynamically compatible model � An artificial variable is introduced in order to keep the equation for the relative velocities in a divergent form. � The term can be considered as the true source term because the following compatibility condition holds 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Theory II. Governing Equations dissipative production & energy conservation � dissipative production � energy conservation � The system of thermodynamically compatible equations is hyperbolic and all equations are in a divergent form. 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Numerical method � High accuracy Runge-Kutta-WENO method 3 rd order in time and 5 th order in space (Shu, C. W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. NASA/CR-97 -206253, ICASE. report No. 97 -65. 1997) � Differential equations of the model in a two-dimensional coordinate system may be write out in the following vector form the Runge-Kutta-WENO method for solving the system in a rectangular area , where ). � The difference approximation of the equation may be written out in the form � � with cells If the values of fluxes on lateral faces of a cell are known, one can obtain the differential equation for solution values in a cell which is solved by the Runge-Kutta method of the required order of accuracy. (Kennedy, C. A. and Carpenter, M. H. Additive Runge-Kutta schemes for convection-diffusion-reaction equations. NASA Langley Technical Report Server, 2001) 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Numerical method � High accuracy Runge-Kutta-WENO method 3 rd order in time and 5 th order in space � The formulae for the TVD Runge-Kutta method of the third order of accuracy are of the form (Drikakis, D. and Rider, W. J. High-resolution methods for incompressible and low-speed flows. Springer-Verlag, 2004) 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

Numerical method � High accuracy Runge-Kutta-WENO method 3 rd order in time and 5 th order in space � To specify the values of fluxes on the faces of the computational cells it is sufficient to know the values of on the cell faces. � To calculate fluxes on cell faces the WENO approximation of the solution by polynomials (reconstruction) is implemented using the solution values in neighbor cells. A decomposition with respect to space variables is employed, i. e. for calculating and one-dimensional systems are used which describe the propagation of waves along the axes � The Lax–Friedrichs method is employed to calculate fluxes in the equations. For the equation in the direction of the axis, assuming that in the initial data the values and of point are known, calculate the flux in this point by the formula � Analogically for on the left and right axis, 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

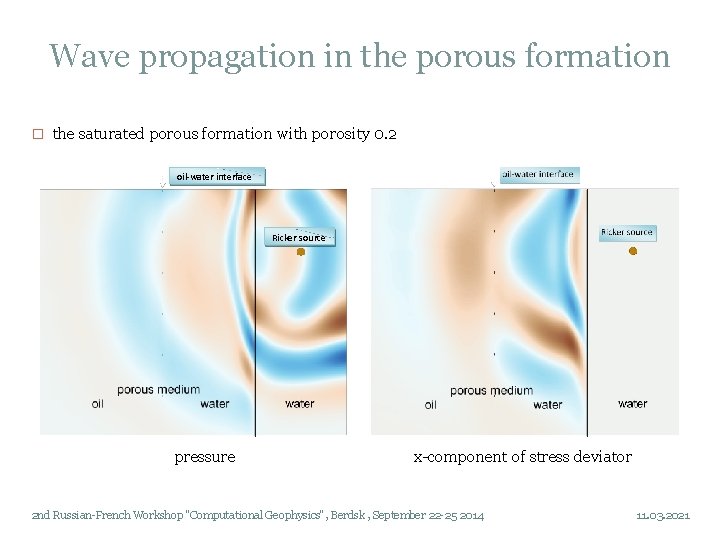
Wave propagation in the porous formation � the saturated porous formation with porosity 0. 2 oil-water interface Ricker source pressure x-component of stress deviator 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

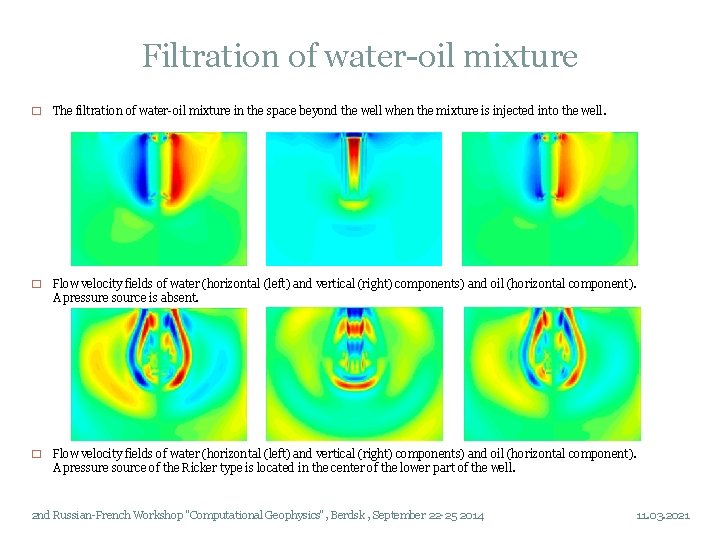
Filtration of water-oil mixture � The filtration of water-oil mixture in the space beyond the well when the mixture is injected into the well. � Flow velocity fields of water (horizontal (left) and vertical (right) components) and oil (horizontal component). A pressure source is absent. � Flow velocity fields of water (horizontal (left) and vertical (right) components) and oil (horizontal component). A pressure source of the Ricker type is located in the center of the lower part of the well. 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021

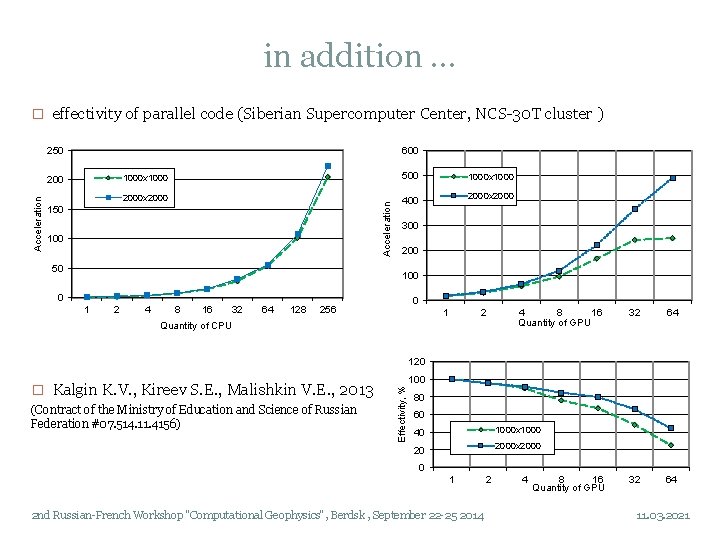
in addition … � effectivity of parallel code (Siberian Supercomputer Center, NCS-30 Т cluster ) 250 600 1000 x 1000 500 1000 x 1000 2000 x 2000 400 2000 x 2000 Acceleration 200 150 100 50 300 200 100 0 1 2 4 8 16 32 64 128 0 256 1 2 Quantity of CPU 4 8 16 Quantity of GPU 32 64 120 (Contract of the Ministry of Education and Science of Russian Federation #07. 514. 11. 4156) 100 Effectivity, % � Kalgin K. V. , Kireev S. E. , Malishkin V. E. , 2013 80 60 40 1000 x 1000 20 2000 x 2000 0 1 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 2 4 8 16 Quantity of GPU 11. 03. 2021

Conclusions � The new computational model of multiphase compressible flow in saturated elastic porous media is proposed. The governing equations of the model form the hyperbolic system of differential equations in a divergent form. The above properties allow one to apply high accuracy numerical methods to solve the variety of problems. � The proposed model allows one to study the propagation of seismoacoustic waves accompanied by dissipative effects and temperature variations in well systems, the influence of stress waves on the flow of fluid (water, oil, their mixture) in deforming porous media, and processes of finite elastic deformations of porous medium saturated by the compressible multiphase fluid. 2 nd Russian-French Workshop "Computational Geophysics", Berdsk , September 22 -25 2014 11. 03. 2021