Modeling n n n Define volumetric objects in

Modeling n n n Define volumetric objects in terms of surfaces patches that surround the volume Each surface patch is approximated set of polygons Each polygon is specified by a set of vertices To pass the object through the graphics pipeline, pass the vertices of all polygons through a number of transformations using homogeneous coordinates All transformation are linear in homogeneous coordinates, thus a implemented as matrix multiplications Hierarchical Modeling Hofstra University 1

Hierarchical Modeling: Tree of Transformations, Display Lists and Functions, Matrix and Attribute Stacks, Hierarchical Modeling Hofstra University 2

Hierarchical Modeling and Structures n n n Motivation: complex modeling, multiple instances, modularity To model a complex object or a scene: use a tree to model the hierarchy primitives that can be drawn directly, at leaves internal node become instances transformations that position instances of objects label the edges Traverse in pre-order to generate code for the scene Hierarchical Modeling Hofstra University 3
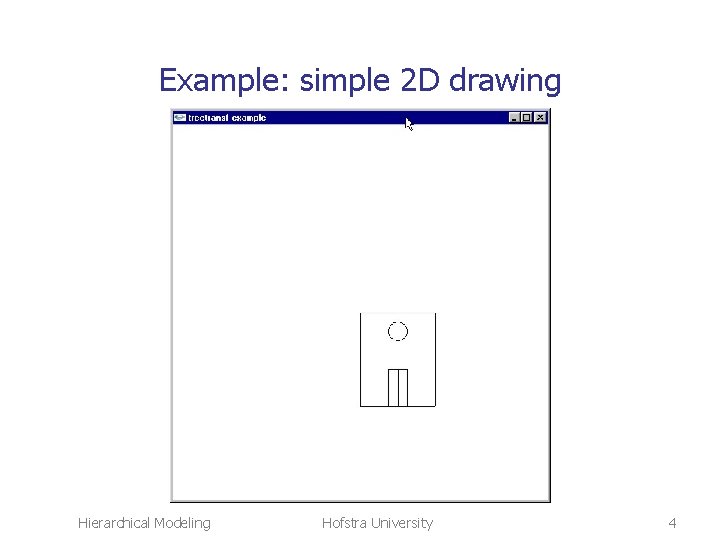
Example: simple 2 D drawing Hierarchical Modeling Hofstra University 4
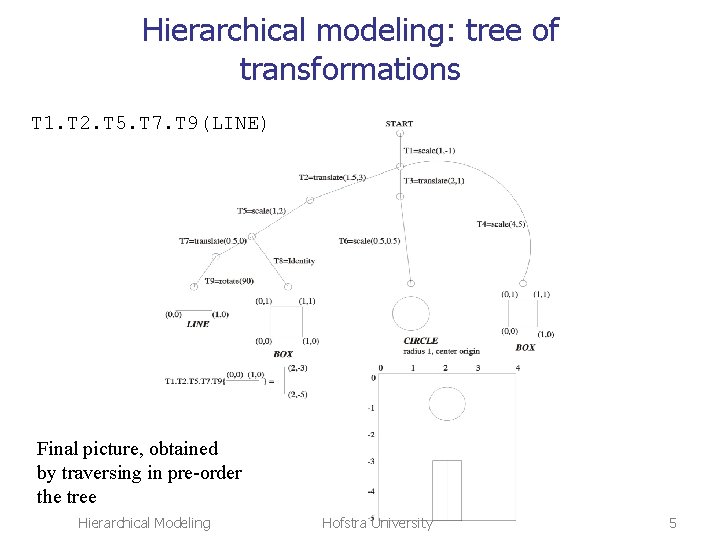
Hierarchical modeling: tree of transformations T 1. T 2. T 5. T 7. T 9(LINE) Final picture, obtained by traversing in pre-order the tree Hierarchical Modeling Hofstra University 5

Compress the tree n n n If an edge (A, B) is labeled with identity transformation, remove it , and move any drawings from node B into A If edges (A, B) and (A, C) have the same labels, merge the nodes B and C Example: in the previous tree T 8 will be removed, and the unit square moved to the parent node Hierarchical Modeling Hofstra University 6

From the tree model to Open. GL code n n Start from the root, traverse tree in pre-order When visiting a node, if there is a primitive at the node that can be drawn, draw it If going down from a node which has more then one unvisited child, store(push) CTM and attributes before continuing down If coming back up an edge to a node which has unvisited children, pop CTM and attributes Hierarchical Modeling Hofstra University 7

Stack implementation of the compressed tree gl. Scalef(1. 0, -1. 0, 1. 0); //T 1 gl. Push. Matrix(); gl. Translatef(1. 5, 3. 0, 0. 0); //T 2 gl. Scalef(1. 0, 2. 0, 1. 0); //T 5 gl. Begin(GL_LINE_LOOP); //BOX gl. Vertex 3 f(0. 0, 0. 0); gl. Vertex 3 f(1. 0, 0. 0); gl. Vertex 3 f(0. 0, 1. 0, 0. 0); gl. End(); gl. Translatef(0. 5, 0. 0); //T 7 gl. Rotatef(90. 0, 1. 0); //T 9 gl. Begin(GL_LINES); //LINE gl. Vertex 3 f(0. 0, 0. 0); gl. Vertex 3 f(1. 0, 0. 0); gl. End(); Hierarchical Modeling gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translatef(2. 0, 1. 0, 0. 0); //T 3 gl. Scalef(0. 5, 1. 0); //T 6 draw. Unit. Circle(NUM_SLICES); gl. Pop. Matrix(); gl. Scalef(4. 0, 5. 0, 1. 0); // T 4 gl. Begin(GL_LINE_LOOP); // BOX gl. Vertex 3 f(0. 0, 0. 0); gl. Vertex 3 f(1. 0, 0. 0); gl. Vertex 3 f(0. 0, 1. 0, 0. 0); gl. End(); gl. Flush(); Hofstra University 8

Examples n n Model a 2 D cart consisting of a rod and 2 wheels positioned symmetricly wrt to the rod’s middle point. Spin the wheels (Animation, Double Buffering) Animate 2 D robot HW: Model hierarchically a 3 D scene consisting of a circular road, a car, and a at least 2 trees along the road. Each component has a different color than the rest. Feel free to expand. A car has a rectangular body and 4 wheels n A tree has a trunk (cylinder) and a crown (sphere) n The road is a circular loop or a narrow rectangular strip n Model each object (object part) in its own local coordinate system; use transformations to position all objects in the scene n Use functions or display lists to model the components n HW is due after we come back from Spring break: submit the source code, in the report in addition to the usual things (I. e. what you did; How you did it, etc. ), draw by hand the tree of transformations you used to model the scene hierarchy. Hierarchical Modeling Hofstra University 9 n

Display Lists n Need to draw the display at a rate sufficient to avoid noticeable flicker Hierarchical Modeling Hofstra University 10
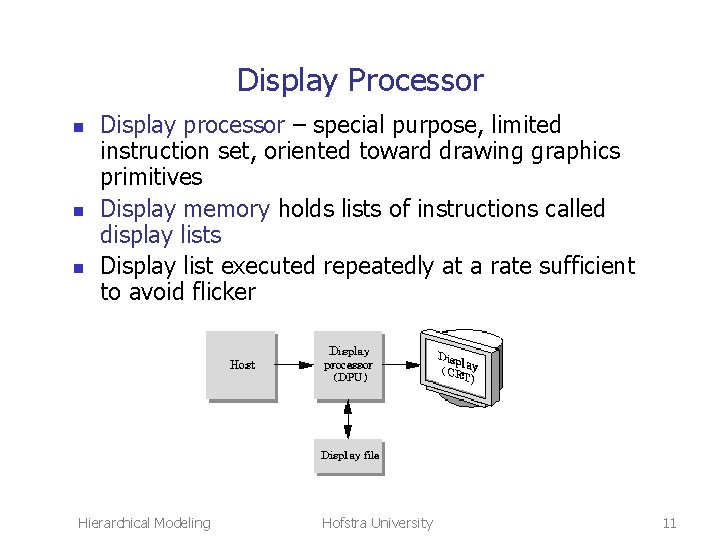
Display Processor n n n Display processor – special purpose, limited instruction set, oriented toward drawing graphics primitives Display memory holds lists of instructions called display lists Display list executed repeatedly at a rate sufficient to avoid flicker Hierarchical Modeling Hofstra University 11

Display Modes n n n Immediate Mode – as soon as the program executes a statement that defines a primitive, it is sent to the server Retained Mode – define the object once, then put its description in a display list. Redisplayed with a simple function call Reduced network traffic Hierarchical Modeling Hofstra University 12

Open. GL Display Lists #define BOX 1 gl. New. List(BOX, GL_COMPILE); gl. Begin(GL_POLYGON); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 2 f(-1. 0, -1. 0); gl. Vertex 2 f( 1. 0, 1. 0); gl. Vertex 2 f(-1. 0, 1. 0); gl. End( ); gl. End. List( ); Send list to server but don’t display contents GL_COMPILE_AND_EXECUTE This can change the original state and leave it altered gl. Call. List(BOX); Hierarchical Modeling Hofstra University 13

Definition and Execution #define BOX 1 gl. New. List(BOX, GL_COMPILE); gl. Push. Attrib(GL_ALL_ATTRIB_BITS); gl. Push. Matrix( ); gl. Begin(GL_POLYGON); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 2 f(-1. 0, -1. 0); Push and pop gl. Vertex 2 f( 1. 0, -1. 0); attributes and coordinates gl. Vertex 2 f( 1. 0, 1. 0); to the stack gl. Vertex 2 f(-1. 0, 1. 0); gl. End( ); gl. Pop. Attrib( ); gl. Pop. Matrix( ); gl. End. List( ); Hierarchical Modeling Hofstra University 14

Stack implementation of the tree of transformations gl. Scalef(1. 0, -1. 0, 1. 0); gl. Push. Matrix(); gl. Translatef(1. 5, 3. 0, 0. 0); gl. Scalef(1. 0, 2. 0, 1. 0); gl. Call. List(BOX); gl. Translatef(0. 5, 0. 0); gl. Rotatef(90. 0, 1. 0); gl. Begin(GL_LINES); gl. Vertex 3 f(0. 0, 0. 0); gl. Vertex 3 f(1. 0, 0. 0); gl. End(); Hierarchical Modeling gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translatef(2. 0, 1. 0, 0. 0); gl. Scalef(0. 5, 1. 0); draw. Unit. Circle(NUM_SLICES); gl. Pop. Matrix(); gl. Scalef(4. 0, 5. 0, 1. 0); gl. Call. List(BOX); gl. Flush(); Hofstra University 15

Example: cart with two wheels Hierarchical Modeling Hofstra University 16

Example: wheel Model a red wheel of radius WHEEL_RAD, consisting of a circle and two crossed spikes. Primitive components are unit circle and crossed orthogonal spikes of length 2. gl. New. List(WHEEL, GL_COMPILE); gl. Push. Matrix(); gl. Push. Attrib(GL_COLOR); // red wheel with WHEEL_RAD gl. Color 3 f(1. 0, 0. 0); // red gl. Scalef(WHEEL_RAD, 1. 0); // scale the unit wheel gl. Begin(GL_LINES); // unit cross gl. Vertex 2 f( -1. 0, 0. 0); gl. Vertex 2 f( 0. 0, -1. 0); gl. Vertex 2 f( 0. 0, 1. 0); gl. End(); draw. Unit. Circle(NUM_SLICES); gl. Pop. Attrib(); gl. Pop. Matrix(); gl. End. List(); Hierarchical Modeling // unit circle Hofstra University 17

Example: rod with 2 fixed wheels Model the cart consisting of two red wheels of radius WHEEL_RAD, positioned at the ends of a green rod of length 2*HALF_AXIS_LENGTH. The two wheels are rotated at different angles. gl. New. List(CART, GL_COMPILE); gl. Push. Matrix(); gl. Push. Attrib(GL_COLOR); gl. Color 3 f(0. 0, 1. 0, 0. 0); // green gl. Begin(GL_LINES); // rod gl. Vertex 2 f(-HALF_AXIS_LENGTH, 0. 0); gl. Vertex 2 f( HALF_AXIS_LENGTH, 0. 0); gl. End(); gl. Push. Matrix(); gl. Translatef(-HALF_AXIS_LENGTH, 0. 0); //position front WHEEL at axis gl. Rotatef(TH, 0. 0, 1. 0); // rotate a WHEEL by TH gl. Call. List(WHEEL); gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translatef(HALF_AXIS_LENGTH, 0. 0); //position back WHEEL at axis gl. Rotatef(TH+INCR, 0. 0, 1. 0); // rotate a WHEEL by TH+INCR gl. Call. List(WHEEL); gl. Pop. Attrib(); gl. Pop. Matrix(); gl. End. List(); Hierarchical Modeling Hofstra University 18

Example: cart with 2 wheels void display() { gl. Clear(GL_COLOR_BUFFER_BIT); gl. Call. List(CART); gl. Flush(); } void myinit() { gl. Clear. Color(1. 0, 0. 0); gl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); glu. Ortho 2 D(-225. 0, -225, 225. 0); gl. Matrix. Mode(GL_MODELVIEW); } define. Parts(); // WHEEL and CART are display lists defined here, main() …. As usual, negotiate with Windows Sys, register callbacks, run loop to process events Hierarchical Modeling Hofstra University 19

Example: spin the wheels n n Limitations of display lists Use of functions in drawing instances of objects at tree nodes Continuously keep changing the value of rotation angle for turning a wheel Need of double buffering Hierarchical Modeling Hofstra University 20

Example: spin the wheels, 2 void draw_cart() { gl. Push. Matrix(); gl. Push. Attrib(GL_COLOR); gl. Color 3 f(0. 0, 1. 0, 0. 0); // draw axis in green gl. Begin(GL_LINES); gl. Vertex 2 f(-HALF_AXIS_LENGTH, 0. 0); gl. Vertex 2 f(HALF_AXIS_LENGTH, 0. 0); gl. End(); gl. Push. Matrix(); gl. Translatef(-HALF_AXIS_LENGTH, 0. 0); // position front wheel at axis, T 1 gl. Rotatef(theta, 0. 0, 1. 0); // spin front WHEEL by theta gl. Call. List(WHEEL); // draw wheel gl. Pop. Matrix(); gl. Translatef(HALF_AXIS_LENGTH, 0. 0); // position back wheel at axis, T 2 gl. Rotatef(theta, 0. 0, 1. 0); // spin back WHEEL by theta gl. Call. List(WHEEL); // draw wheel gl. Pop. Attrib(); gl. Pop. Matrix(); } Hierarchical Modeling Hofstra University 21

Open GL interactive program structure int main(int argc, char** argv) { glut. Init(&argc, argv); glut. Init. Display. Mode (GLUT_SINGLE | GLUT_RGB); glut. Create. Window(”generic example"); myinit (); glut. Reshape. Func (my. Reshape); glut. Mouse. Func (mouse); glut. Motion. Func(do_on_motion); glut. Idle. Function(idle); glut. Display. Func(display); glut. Main. Loop(); } Hierarchical Modeling Hofstra University 22

Example: spin the wheels, 3, the Idle Function void idle(void) { theta += INCR_ANGLE; glut. Post. Redisplay(); } void mouse. Motion(int x, int y) { transx = x; transy = y; glut. Post. Redisplay(); } void display() { gl. Clear(GL_COLOR_BUFFER_BIT); // IDLE callback function updates // rotation angle that spins a wheel // MOTION callback function updates // translation vector that moves whole // DISPLAY callback draws whole object // in back buffer then swaps buffers // translate whole object axis with spinning wheels gl. Translatef( (float)transx, (float)(WINDOWH-transy), 0. 0); draw_cart(); } glut. Swap. Buffers(); Hierarchical Modeling // SWAP BUFFERS Hofstra University 23

Example: spin the wheels, 4, the Idle Function int main(…) { glut. Init. Display. Mode(GLUT_DOUBLE|GLUT_RGB); // double buffering. . . glut. Display. Func(display); glut. Motion. Func(mouse. Motion); glut. Idle. Func(idle); glut. Main. Loop(); … } Hierarchical Modeling Hofstra University 24

Example: model circular road // ROAD_RAD 1, ROAD_RAD 2, ROAD_SL, ROAD_RINGS defined globally void draw_road() { GLUquadric* q; q = glu. New. Quadric(); // dynamic array to hold vertices of road // creates and returns a ptr to new quadric object gl. Push. Matrix(); gl. Push. Attrib(GL_ALL_ATTRIB_BITS); gl. Color 3 f(0. 5, 0. 5); // road is gray glu. Disk(q, ROAD_RAD 1, ROAD_RAD 2, ROAD_SL, ROAD_RINGS); gl. Pop. Matrix(); gl. Pop. Attrib(); } glu. Delete. Quadric(q); Hierarchical Modeling Hofstra University 25

Example: model circular road void display() { gl. Clear(GL_COLOR_BUFFER_BIT); // gl. Rotatef(45, 1. 0, 0. 0); //glu. Look. At(0. 0, -1. 0, 0. 0, 1. 0); draw_road(); gl. Flush(); } Hierarchical Modeling Hofstra University 26

Modeling complex objects/motion n n Decompose object hierarchically into parts Model each part in local frame, and use affine transformations to position it at its proper place in the part above it in the hierarchy Hierarchical Modeling Hofstra University 27
- Slides: 27