Modeling lattice modular systems with space groups Nicolas

Modeling lattice modular systems with space groups Nicolas Brener, Faiz Ben Amar, Philippe Bidaud Laboratoire de Robotique de Paris Université de Paris 6

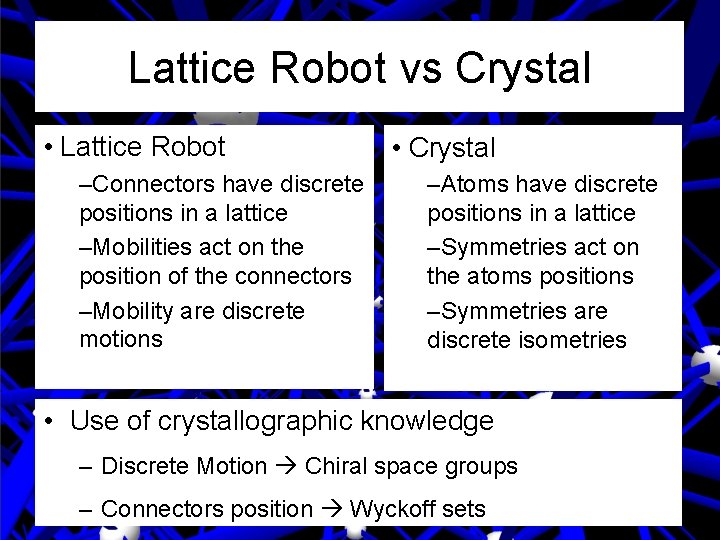
Lattice Robot vs Crystal • Lattice Robot –Connectors have discrete positions in a lattice –Mobilities act on the position of the connectors –Mobility are discrete motions • Crystal –Atoms have discrete positions in a lattice –Symmetries act on the atoms positions –Symmetries are discrete isometries • Use of crystallographic knowledge – Discrete Motion Chiral space groups – Connectors position Wyckoff sets

Outline • Discrete motion spaces – Point groups – Lattice groups – Space groups • • • Wyckoff positions Group hierarchy Classification of lattice robots Design of lattice robots Next steps

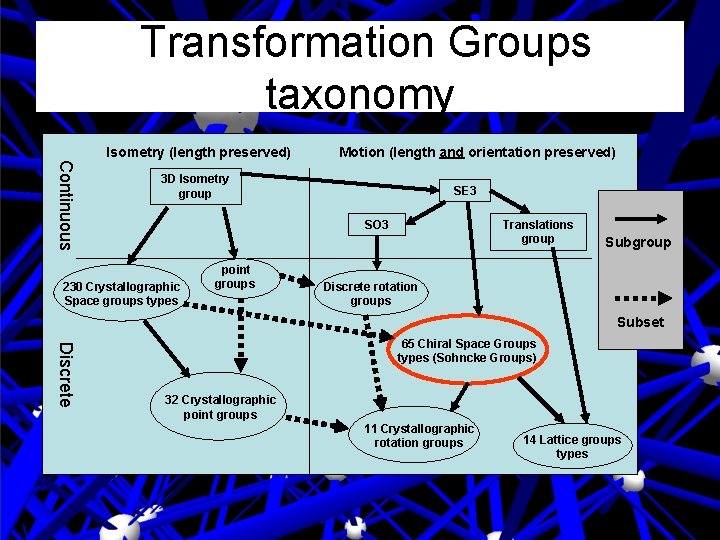
Transformation Groups taxonomy Isometry (length preserved) Motion (length and orientation preserved) Continuous 3 D Isometry group SE 3 SO 3 230 Crystallographic Space groups types point groups Translations group Subgroup Discrete rotation groups Subset Discrete 65 Chiral Space Groups types (Sohncke Groups) 32 Crystallographic point groups 11 Crystallographic rotation groups 14 Lattice groups types

Discrete motion spaces • Discrete rotation chiral point group • Discrete translation lattice group • Discrete motion chiral space group

Discrete motion spaces • 11 chiral point groups (rotation groups) Geometric elements – Finite sets • Point group 622 – – 12 rotations 1 6 -fold axes 6 2 -fold axes Generator: { 180° rotation along x, 60° rotation along z } 6 -fold rotation 2 -fold rotation

Discrete motion spaces • Point group 432 – – – Geometric elements 24 rotations 3 4 -fold axes 4 3 -fold axes 6 2 -fold axes Generator: { 90° rotation along x, 90° rotation along y } 4 -fold rotation 3 -fold rotation 2 -fold rotation

Discrete motion spaces • Lattice groups – Infinite sets – Generators: 3 translations – 14 types • Cubic lattice {(a, 0, 0), (0, a, 0), (0, 0, a)} • Cubic centered lattice {(-a, a, a), (a, -a, a), (a, a, a)} • Cubic face centered lattice {(a, a, 0), (a, 0, a), (0, a, a)} • Hexagonal lattice {(a, 0, 0), (a/2, a√ 3/2, h)} • Triclinic lattice {A, B, C}

Discrete motion spaces • Chiral Space Group – Infinite sets – Have rotations and translations (and screw) – 65 types – Described in the « International Tables for Crystallography » edition th. Hahn

Discrete motion spaces Geometric elements of P 622, except screw axes 6 -fold 3 -fold 2 -fold

Discret motion spaces Geometric elements of P 432, except screw axes 4 -fold 3 -fold 2 -fold

Discret motion spaces Geometric elements of F 432, except screw axes 4 -fold 3 -fold 2 -fold

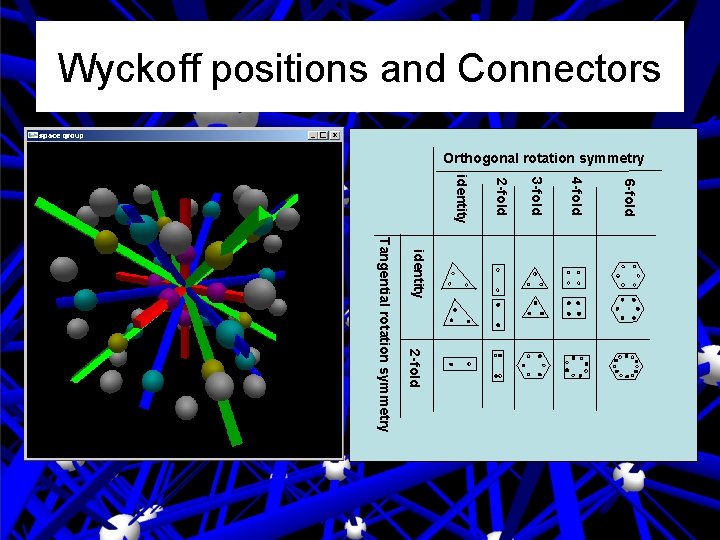
Wyckoff positions and Connectors Orthogonal rotation symmetry 6 -fold 4 -fold 3 -fold 2 -fold identity 2 -fold Tangential rotation symmetry

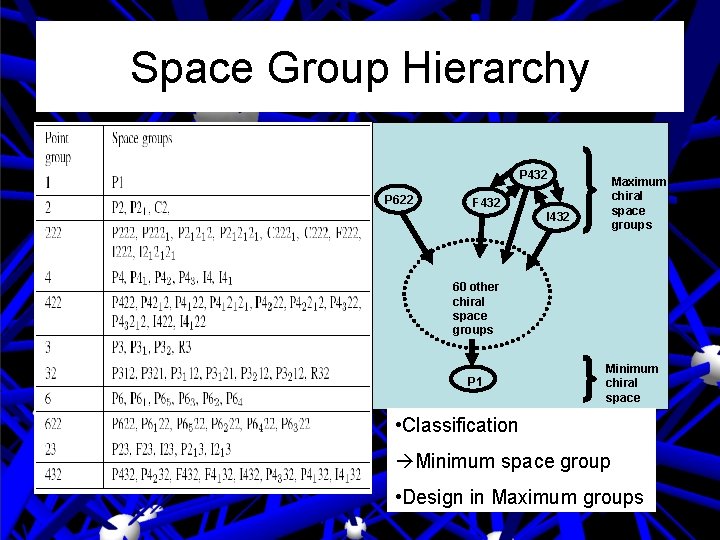
Space Group Hierarchy

Space Group Hierarchy P 432 P 622 Maximum chiral space groups F 432 I 432 60 other chiral space groups P 1 • Classification Minimum chiral space group Minimum space group • Design in Maximum groups

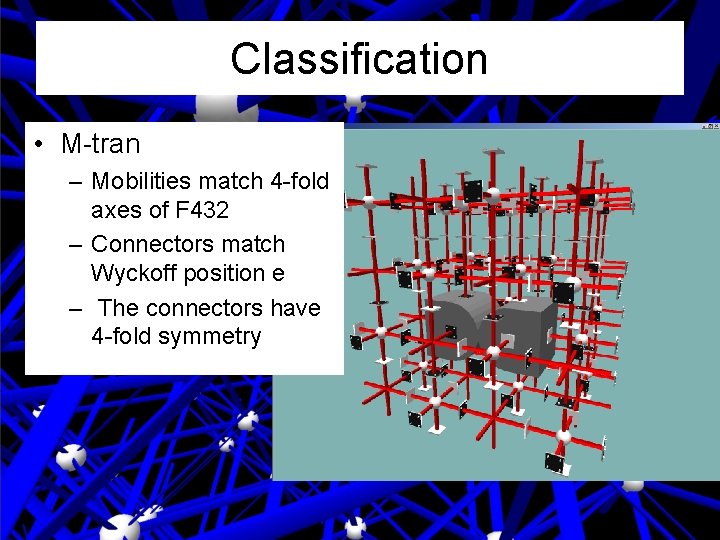
Classification • M-tran – Mobilities match 4 -fold axes of F 432 – Connectors match Wyckoff position e – The connectors have 4 -fold symmetry

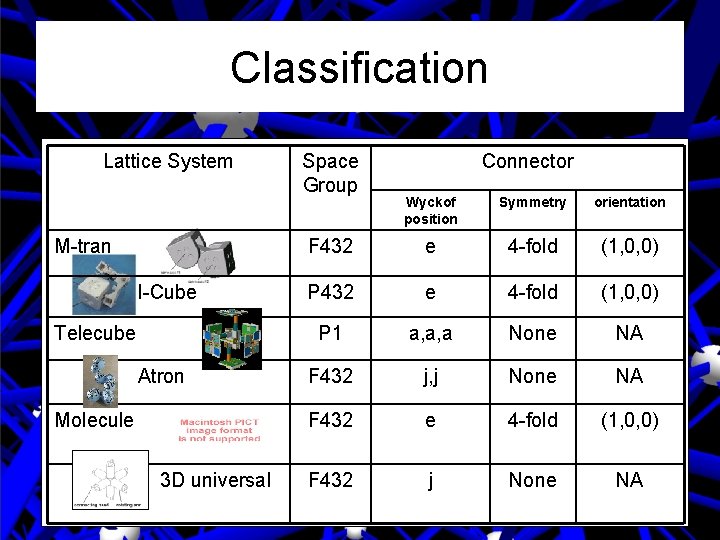
Classification Lattice System M-tran I-Cube Telecube Atron Molecule 3 D universal Space Group Connector Wyckof position Symmetry orientation F 432 e 4 -fold (1, 0, 0) P 1 a, a, a None NA F 432 j, j None NA F 432 e 4 -fold (1, 0, 0) F 432 j None NA

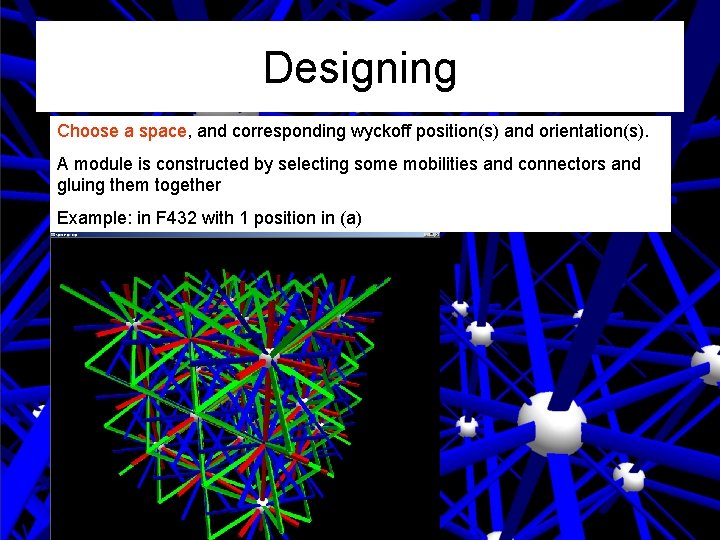
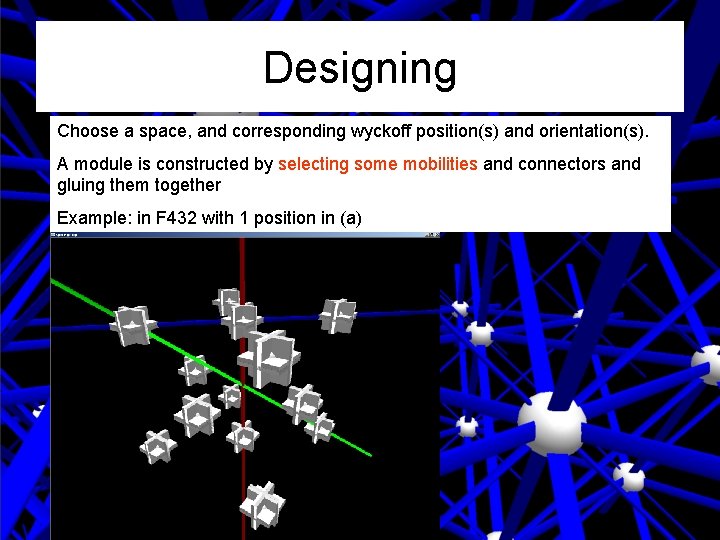
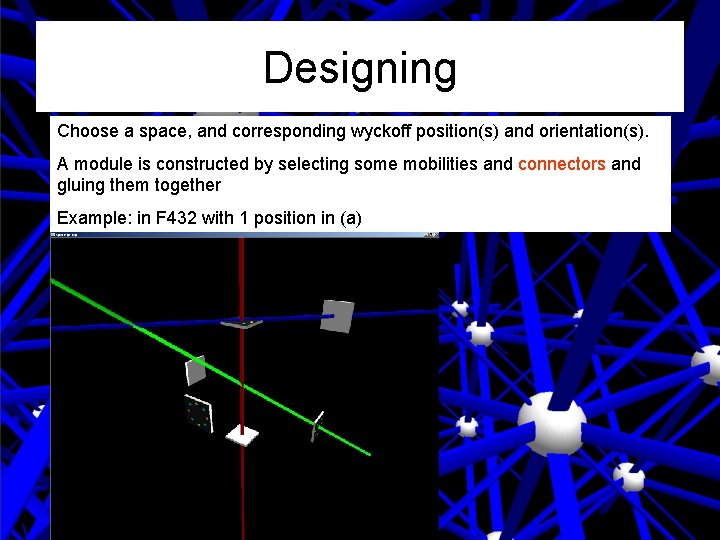
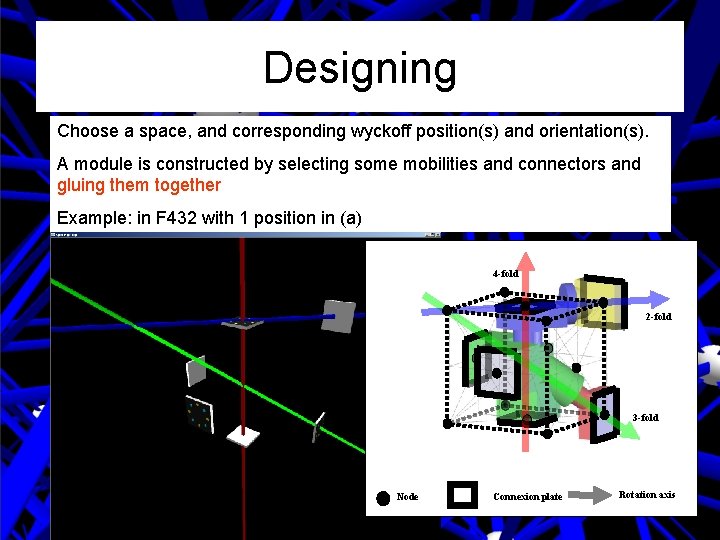
Designing Choose a space, and corresponding wyckoff position(s) and orientation(s). A module is constructed by selecting some mobilities and connectors and gluing them together Example: in F 432 with 1 position in (a)

Designing Choose a space, and corresponding wyckoff position(s) and orientation(s). A module is constructed by selecting some mobilities and connectors and gluing them together Example: in F 432 with 1 position in (a)

Designing Choose a space, and corresponding wyckoff position(s) and orientation(s). A module is constructed by selecting some mobilities and connectors and gluing them together Example: in F 432 with 1 position in (a)

Designing Choose a space, and corresponding wyckoff position(s) and orientation(s). A module is constructed by selecting some mobilities and connectors and gluing them together Example: in F 432 with 1 position in (a)

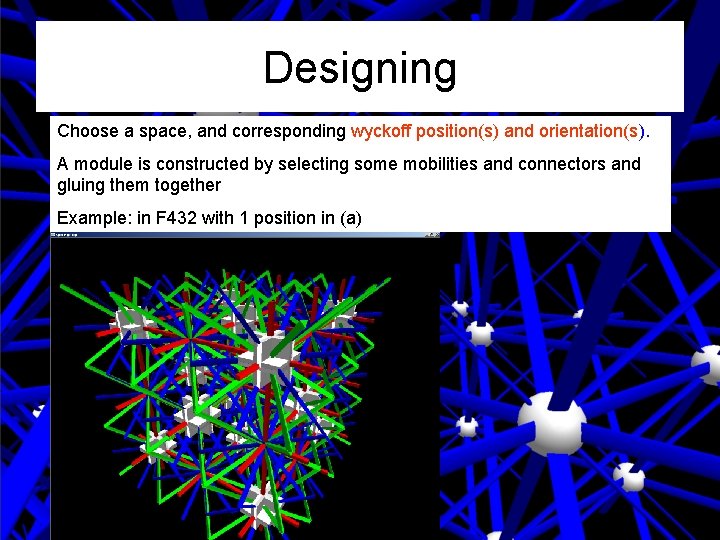
Designing Choose a space, and corresponding wyckoff position(s) and orientation(s). A module is constructed by selecting some mobilities and connectors and gluing them together Example: in F 432 with 1 position in (a) 4 -fold 2 -fold 3 -fold Node Connexion plate Rotation axis

Conclusion • Chiral Space groups give: – All possible mobility – All possible orientation, position and symmetries for connectors • Lattice design but chain type product (ex: M-tran) • Provides a framework to design several compatible systems, or extend existing systems with new modules. • But: it does not provide automatically an operational modular system… – Collision – Joint stops – …

Further steps • Formalize and automate classification. • Find rules on connector positions and mobilities that provide systems that efficiently reconfigure. • Develop a design interface.