Modeling issues when using simulation to test the

Modeling issues when using simulation to test the performance of mathematical programming models under stochastic conditions Anne-Laure Ladier Allen G. Greenwood Gülgün Alpan Univ. Lyon - DISP - INSA Lyon Poznan Univ. of Technology Univ. Grenoble Alpes

Outline Modeling issues when using simulation to test the performance of mathematical programming models under stochastic conditions Context Cases description Foundational differences Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester Operational differences Conclusion 2

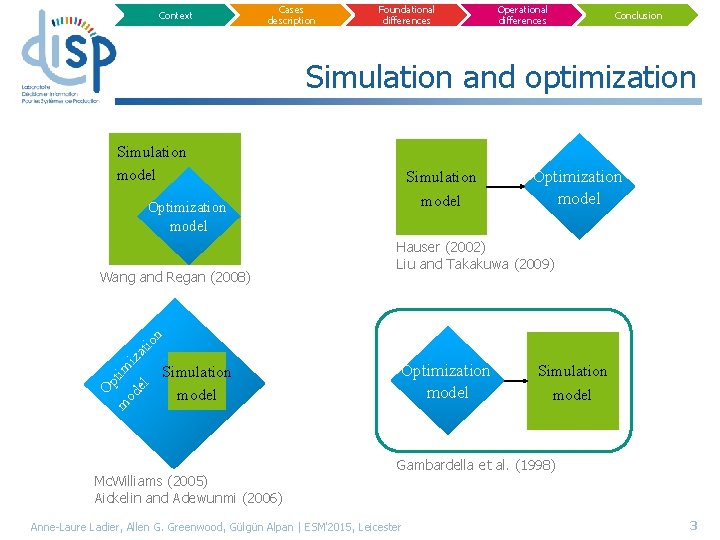
Context Cases description Foundational differences Operational differences Conclusion Simulation and optimization Simulation model Optimization model Hauser (2002) Liu and Takakuwa (2009) Op m tim od i el zati on Wang and Regan (2008) Optimization model Simulation model Mc. Williams (2005) Aickelin and Adewunmi (2006) Optimization model Simulation model Gambardella et al. (1998) Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 3

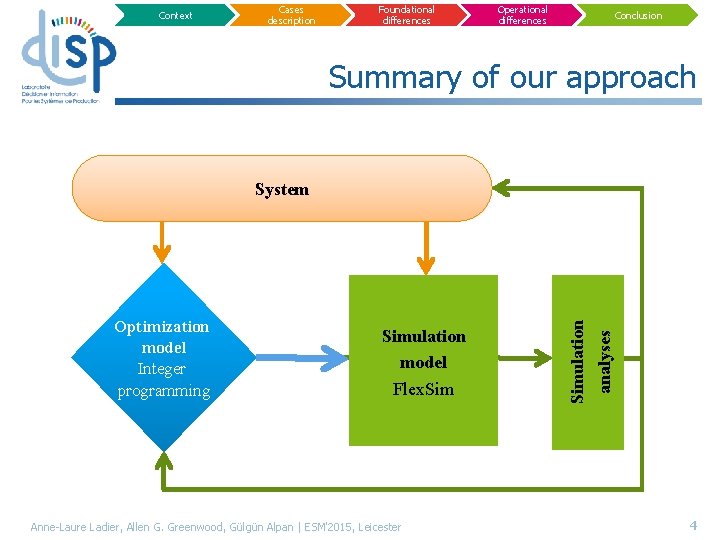
Context Cases description Foundational differences Operational differences Conclusion Summary of our approach Optimization model Integer programming Simulation model Flex. Sim Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester Simulation analyses System 4

Context Cases description Foundational differences Operational differences Conclusion Research questions What are the modelling issues raised by this optimization → simulation relationship? How can they be solved or circumvented? Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 5

Context Cases description Foundational differences Operational differences Conclusion CASES DESCRIPTION Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 6

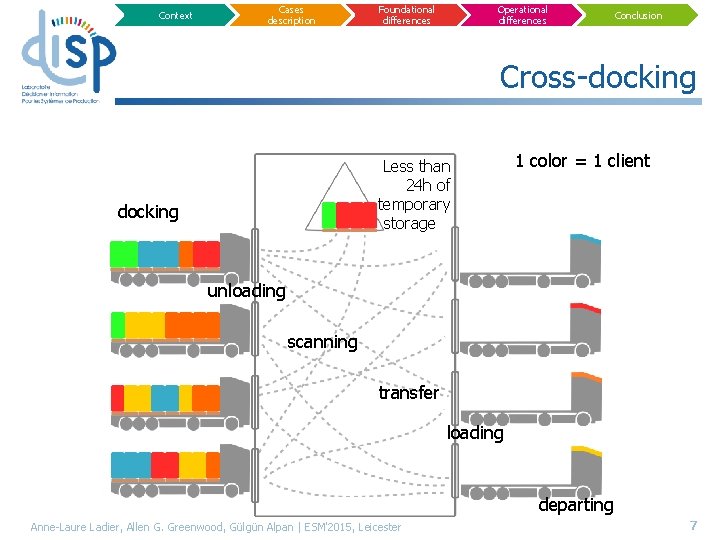
Context Cases description Foundational differences Operational differences Conclusion Cross-docking Less than 24 h of temporary storage docking 1 color = 1 client unloading scanning transfer loading departing Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 7

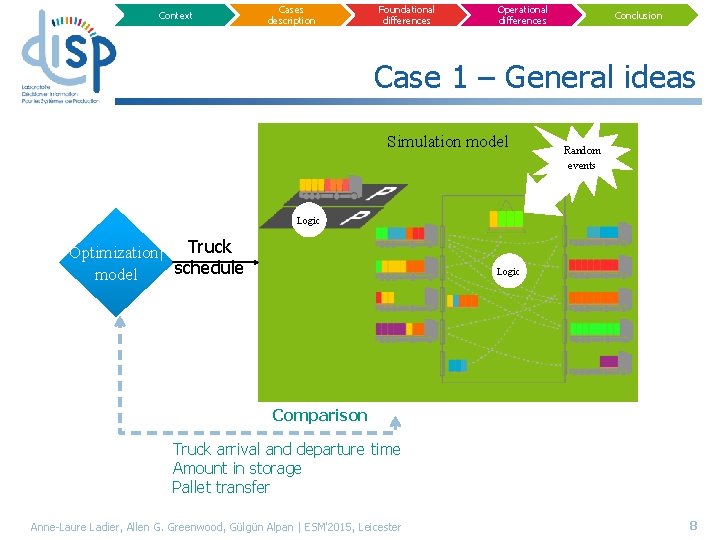
Context Cases description Foundational differences Operational differences Conclusion Case 1 – General ideas Simulation model Random events Logic Truck Optimization schedule model Logic Comparison Truck arrival and departure time Amount in storage Pallet transfer Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 8

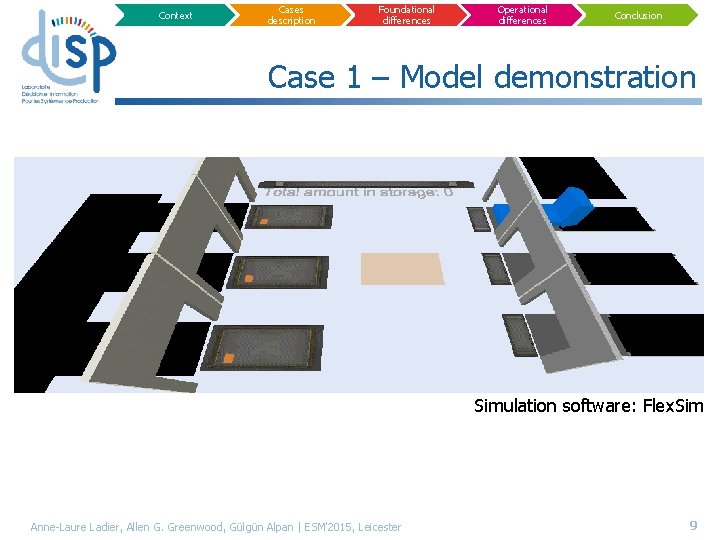
Context Cases description Foundational differences Operational differences Conclusion Case 1 – Model demonstration Simulation software: Flex. Sim Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 9

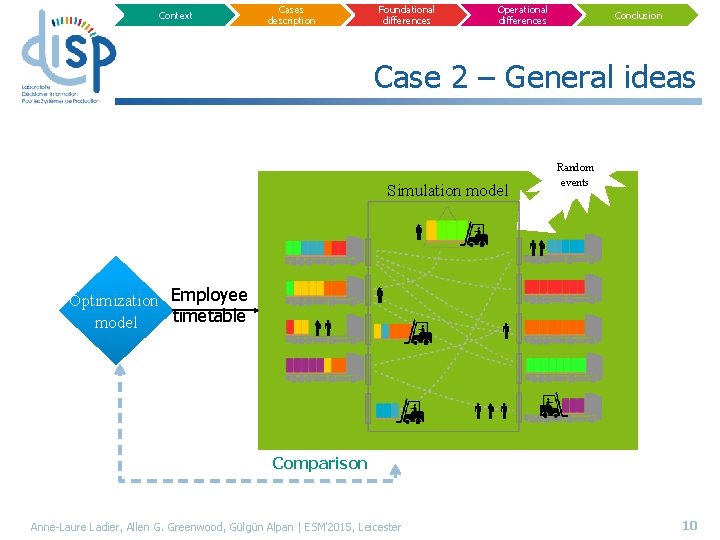
Context Cases description Foundational differences Operational differences Conclusion Case 2 – General ideas Simulation model Random events Optimization Employee timetable model Comparison Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 10

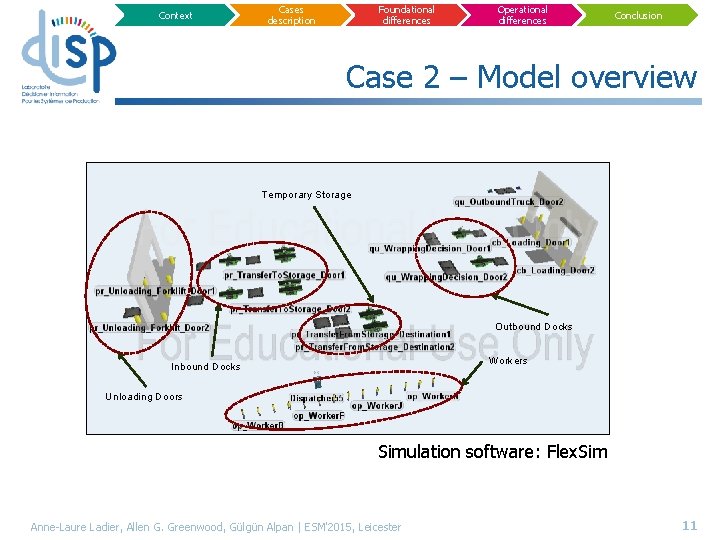
Context Cases description Foundational differences Operational differences Conclusion Case 2 – Model overview Temporary Storage Outbound Docks Workers Inbound Docks Unloading Doors Simulation software: Flex. Sim Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 11

Context Cases description Foundational differences Operational differences Conclusion Two modeling approaches represent the system differently FOUNDATIONAL DIFFERENCES Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 12

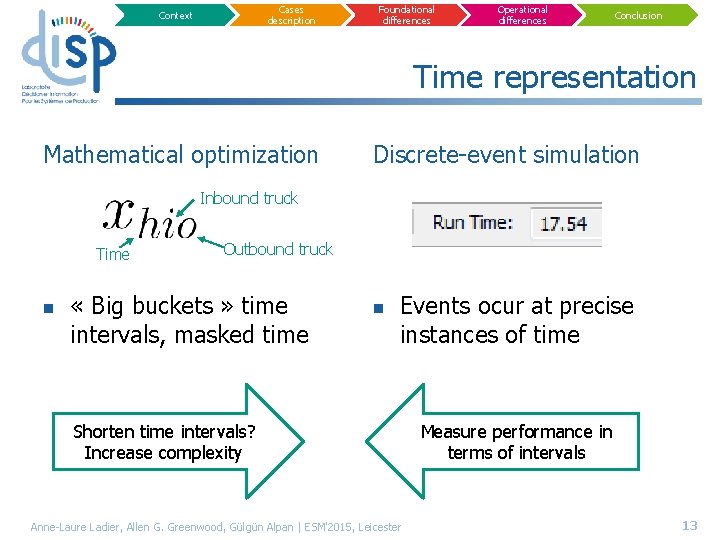
Cases description Context Foundational differences Operational differences Conclusion Time representation Mathematical optimization Discrete-event simulation Inbound truck Time n Outbound truck « Big buckets » time intervals, masked time n Events ocur at precise instances of time Shorten time intervals? Increase complexity Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester Measure performance in terms of intervals 13

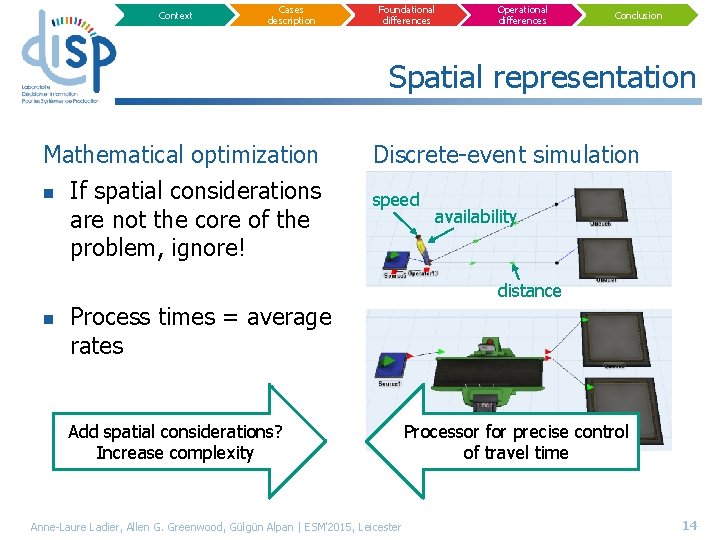
Context Cases description Foundational differences Operational differences Conclusion Spatial representation Mathematical optimization n If spatial considerations are not the core of the problem, ignore! Discrete-event simulation speed availability distance n Process times = average rates Add spatial considerations? Increase complexity Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester Processor for precise control of travel time 14

Context Cases description Foundational differences Operational differences Conclusion Model structure and size Mathematical optimization n Execution time exponential in the instance size Discrete-event simulation n Execution time linear in the instance size Specify size early in the project Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 15

Context Cases description Foundational differences Operational differences Conclusion Make the operations match OPERATIONAL DIFFERENCES Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 16

Context Cases description Foundational differences Operational differences Conclusion Task order, batch size, parallelism Mathematical optimization Discrete-event simulation 3 × 10 pallets/hour 1 pallet= 2 min ≠ 1 × 30 pallets/hour Number of pallets at time h 1 pallet= 6 min No precise task order unless it is a key consideration Order and batch size do have important impacts Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 17

Context Cases description Foundational differences Operational differences Conclusion Process logic Mathematical optimization n n Low granularity: only overall workload in time interval Optimal decision-making Discrete-event simulation n High granularity: specific pallets, doors, workers, etc n FIFO logic n Greedy decision making Operational decisions when deviation from schedule occurs e. g. wait for assigned operator or use available (capable) Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 18

Context Cases description Foundational differences Operational differences Conclusion CONCLUSION Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 19

Context Cases description Foundational differences Operational differences Conclusion After model validation… n The simulation models were used to assess the robustness of the schedules/timetables obtained by mathematical programming A. -L. Ladier, G. Alpan, and A. G. Greenwood, “Robustness evaluation of an IP-based cross-docking schedule using discrete-event simulation, ” in Industrial and Systems Engineering Research Conference, 2014. A. -L. Ladier and G. Alpan, “Robust cross-dock scheduling with time windows, ” European Journal of Operational Research. Under revision. Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 20

Context Cases description Foundational differences Operational differences Conclusion n n n Mathematical programming and optimization are complementary decision-support tools Understand their inherent differences in modeling the same system Encourage n n an increase in the use of discrete-event simulation to assess the performance of optimization models Modelers in sharing their modeling issues/solution to the community Anne-Laure Ladier, Allen G. Greenwood, Gülgün Alpan | ESM'2015, Leicester 21

Thank you for your attention! anne-laure-ladier. fr

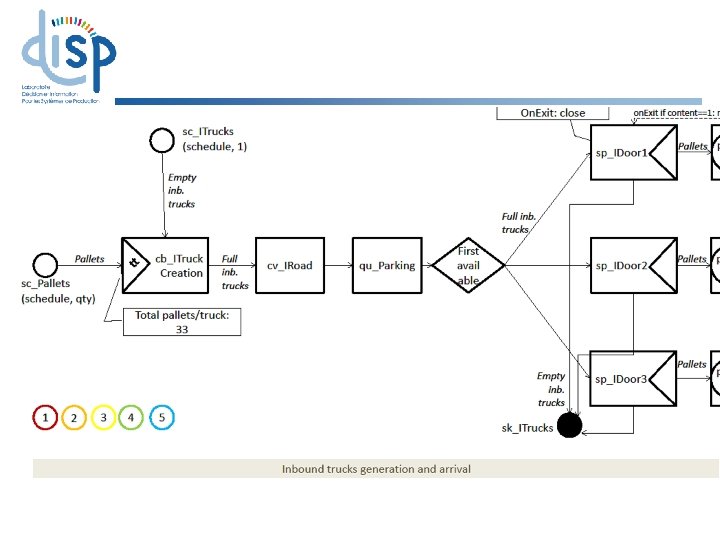
Pallets transfer