Modeling Gene Trees with ContextFree Grammar Heng Li

Modeling Gene Trees with Context-Free Grammar Heng Li The Wellcome Trust Sanger Institute

Overview • Motivation: build accurate gene trees ✤ Conventional: purely from sequence alignment ✤ This talk: combine with the species phylogeny • Method: model trees with CFG (Context. Free Grammar) ✤ TM-WCFG (Weighted CFG) for tree merge ✤ Taxa-SCFG (Stochastic CFG) for gene evolution

Introduction to Context-Free Grammar

Introduction to CFG • Context-free grammar (CFG) is a transformational grammar • Transformational grammar generates strings (or languages) from rules: ✤ Rules: S → SS | a. Sa | b. Sb | aa | bb ✤ Generate baab (derivation): ✤ S⇒b. Sb⇒ba. Sab⇒baa. Saab⇒baab ✤ S⇒SS⇒b. Sb⇒baabb. Sb⇒baab

WCFG and SCFG • WCFG = Weighted Context Free Grammar ✤ Weights assigned to each rule: v→yz • SCFG = Stochastic Context Free Grammar ✤ Probability assigned to each rule: v→yz ✤ ∀v, ∑y, z p(y, z|v)=1 • Rules are applied independently

HMM vs. SCFG • A path of hidden states corresponds to a derivation (parse tree). • SCFG is a superset of HMM (CFG is a superset of FSA): ✤ Viterbi vs. CYK: the optimal derivation ✤ Forward vs. inside: probability of the observation ✤ Baum-Welch vs. Inside-Outside: EM parameter estimation

Tree Merge WCFG

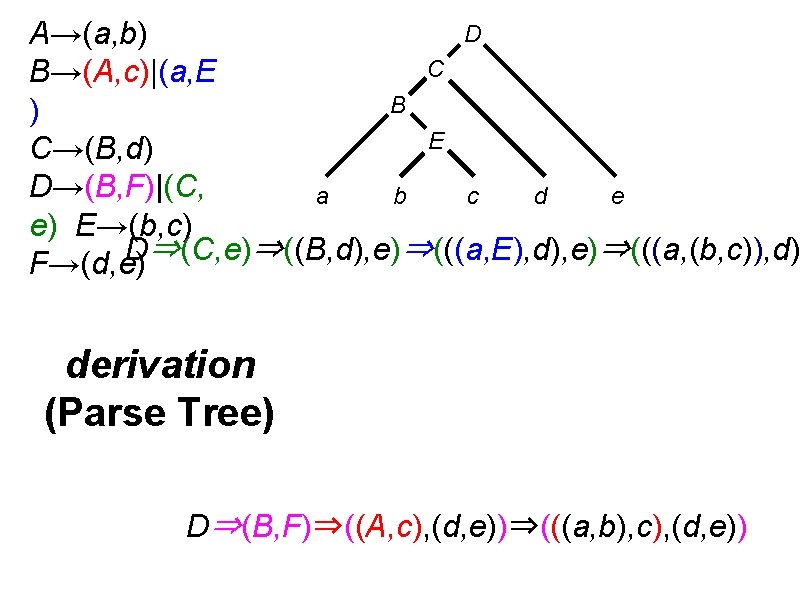
Tree merge problem • Merge several trees with identical leaf set into an optimal tree. • Optimum means: ✤ fewer duplications and losses ✤ higher overall bootstrap support

Overview: tree merge • Input: several gene trees with identical leaves • Output: a gene tree ✤ with each branch coming from one of the input ✤ that optimizes a certain objective function • Procedure: ✤ Calculate bootstrap & infer gene duplications and losses ✤ Generate WCFG rules and their weights from the input ✤ Top-down CYK to find the optimum

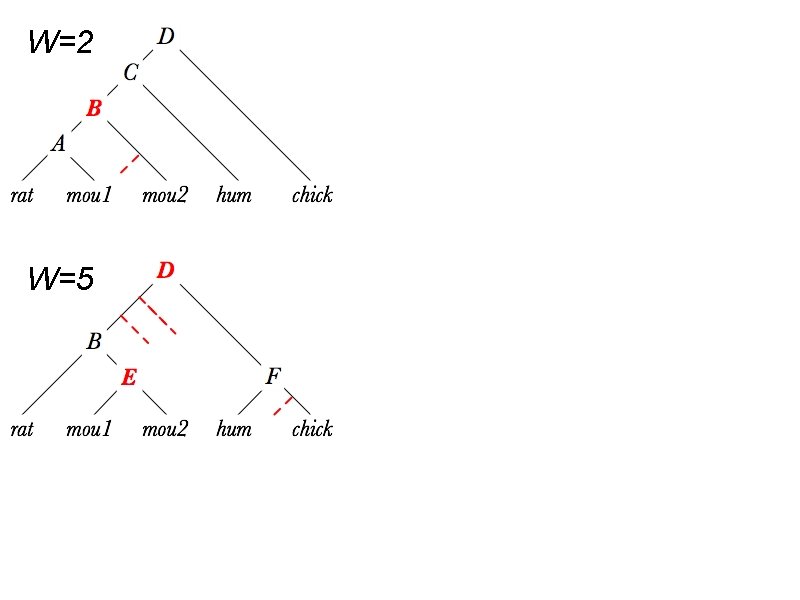
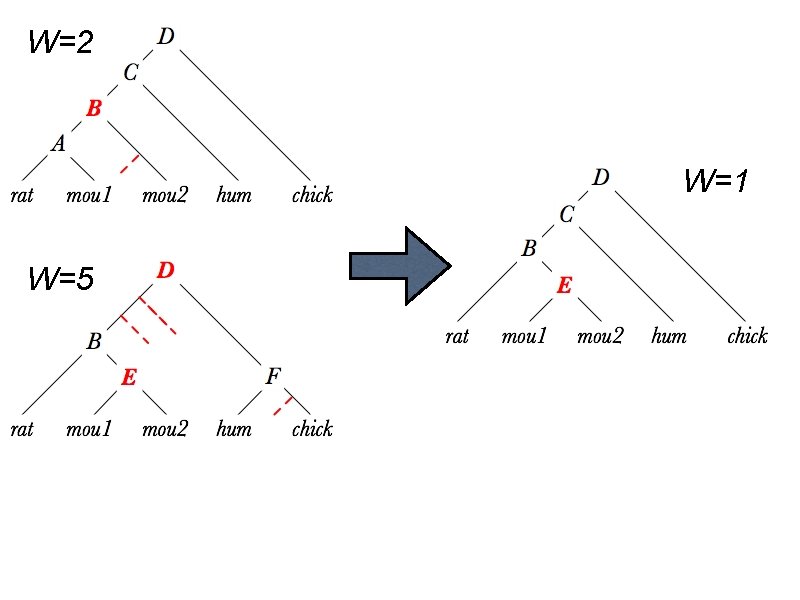
W=2 W=5

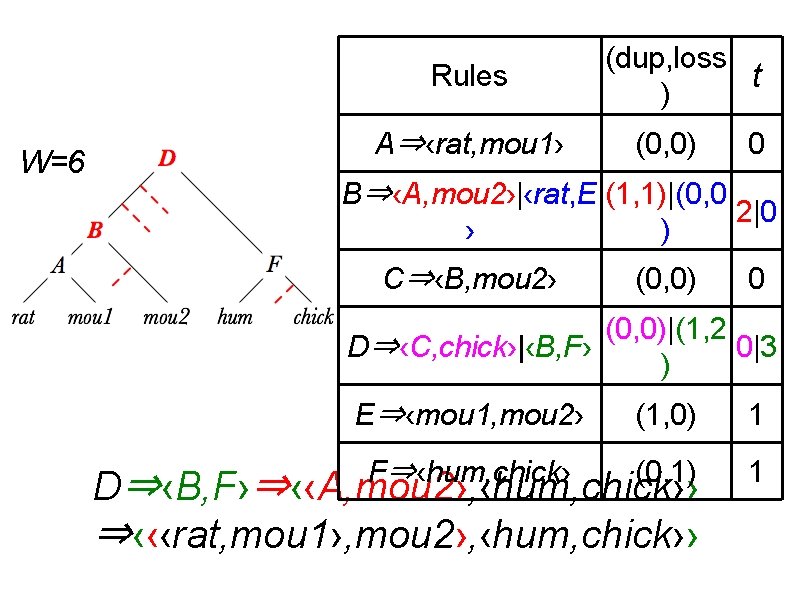
Rules W=6 A⇒‹rat, mou 1› (dup, loss t ) (0, 0) 0 B⇒‹A, mou 2›|‹rat, E (1, 1)|(0, 0 2|0 › ) C⇒‹B, mou 2› (0, 0) 0 (0, 0)|(1, 2 D⇒‹C, chick›|‹B, F› 0|3 ) E⇒‹mou 1, mou 2› (1, 0) 1 F⇒‹hum, chick› (0, 1) 1 D⇒‹B, F›⇒‹‹A, mou 2›, ‹hum, chick›› ⇒‹‹‹rat, mou 1›, mou 2›, ‹hum, chick››

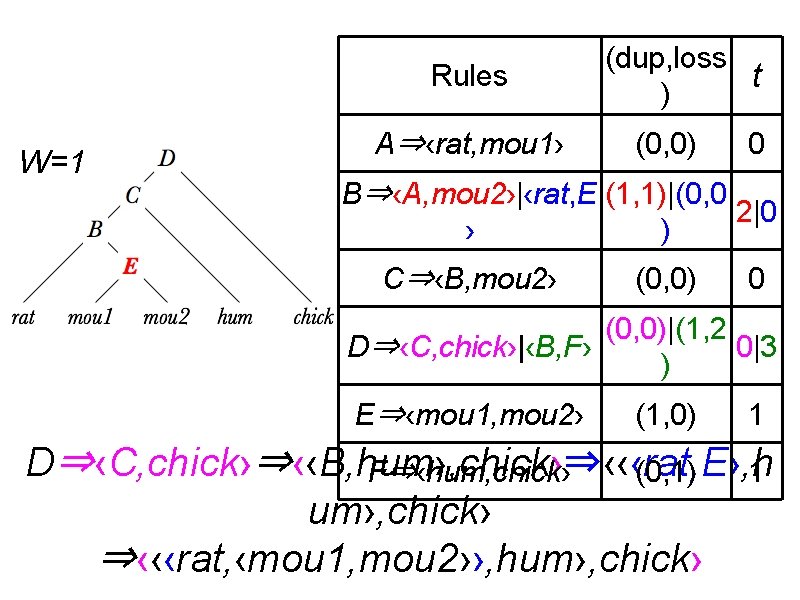
Rules W=1 A⇒‹rat, mou 1› (dup, loss t ) (0, 0) 0 B⇒‹A, mou 2›|‹rat, E (1, 1)|(0, 0 2|0 › ) C⇒‹B, mou 2› (0, 0) 0 (0, 0)|(1, 2 D⇒‹C, chick›|‹B, F› 0|3 ) E⇒‹mou 1, mou 2› (1, 0) 1 D⇒‹C, chick›⇒‹‹B, hum›, chick›⇒‹‹‹rat, E›, h F⇒‹hum, chick› (0, 1) 1 um›, chick› ⇒‹‹‹rat, ‹mou 1, mou 2››, hum›, chick›

W=2 W=1 W=5

Top-down CYK • Cocke-Younger-Kasami (CYK) algorithm • Find the optimum derivation • γ(v): optimum sum of weights up to state v • t(y, z|v): weight of rule v→‹y, z› • γ(v)=max {γ(y)+γ(z)+t(y, z|v)} • Calculated recursively y, z

Weights Independency • A weight for v→‹y, z› must be a function of (v, y, z) • Weights should be additive • Possible weights: ✤ bootstrap ✤ number of duplications and losses.

Taxonomy SCFG

Overview: taxa-SCFG • Taxa-SCFG rules: from a species tree • Taxa-SCFG generates a gene tree ✤ alternative way to infer gene duplications and losses ✤ calculate the probability of a gene tree • A derivation corresponds to a reconciliation ✤ A reconciliation: a consistent assignment of speciations and gene duplications on the gene tree.

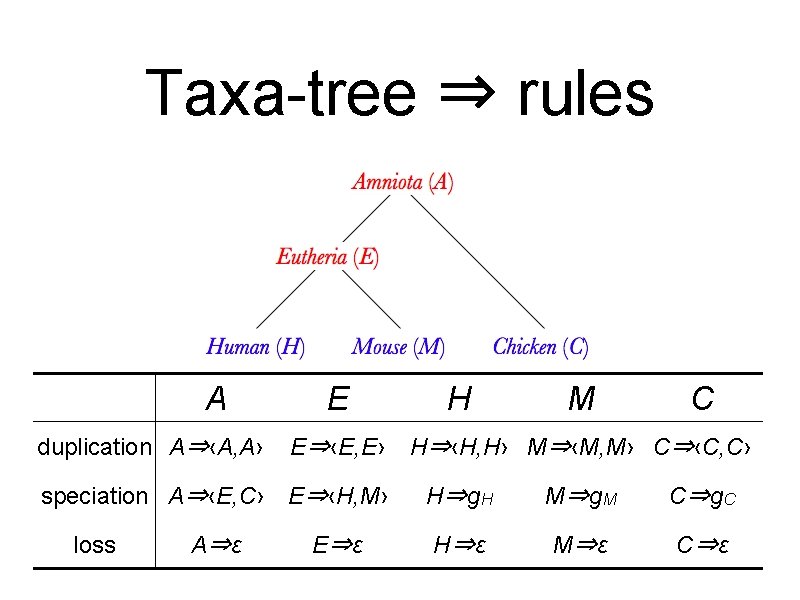
Taxa-tree ⇒ rules A duplication A⇒‹A, A› E E⇒‹E, E› H M C H⇒‹H, H› M⇒‹M, M› C⇒‹C, C› speciation A⇒‹E, C› E⇒‹H, M› H⇒g. H M⇒g. M C⇒g. C A⇒ε H⇒ε M⇒ε C⇒ε loss E⇒ε

Rules ⇒ gene trees

Rules ⇒ gene trees

Taxa-SCFG rules Type W is an internal node W is an external node Rule Probabilit Meaning y W→‹W, W› duplicatio pd(1 -pl) W→‹W 1, W 2 n (1 -pd)(1 -pl) › speciation pl W→ε loss duplicatio W→‹W, W› pd(1 -pl) n W→g. W (1 -pd)(1 -pl) speciation W→ε pl loss

Prob. of a reconciliation ✤ nd: # duplications ✤ nl: # losses ✤ m: # leaves in the species tree ✤ n: # leaves in the gene tree • The most probable π * corresponds to the most parsimonious reconciliation

Prob. of a gene tree • P(G|X, S)=P(G|X)∙P(G|S) ✤ P(G|X): prob. from seq. alignment X ✤ P(G|S): prob. from species tree S • P(G|S) can be approximated as P(G, π*|S) where π* is the most probable reconciliation • In theory, P(G|S) can be calculated with an alternative SCFG model

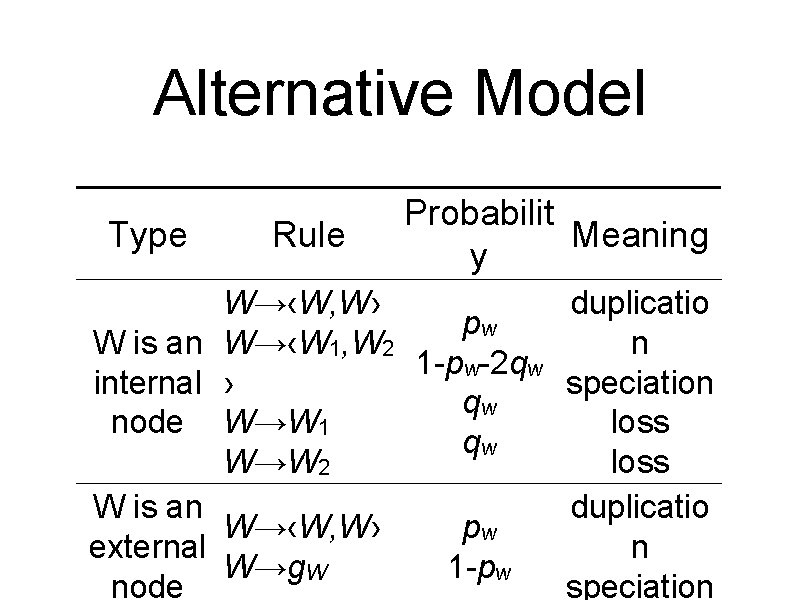
Alternative Model Type Rule Probabilit Meaning y W→‹W, W› pw W is an W→‹W 1, W 2 1 -pw-2 qw internal › qw node W→W 1 qw W→W 2 W is an W→‹W, W› pw external W→g. W 1 -pw node duplicatio n speciation loss duplicatio n speciation

Implementation & Evaluation

Reconstruct gene trees • Species aware ML (find a gene tree G that maximizes P(G|X, S)): ✤ Calculate P(G|X) with Phy. ML ✤ Infer π* with parsimonious reconciliation ✤ Maximize P(G|X)∙P(G, π*|S) with a Phy. ML-typed search • Tree merge (five trees): ✤ NJ-d. S, NJ-d. N, NJ-p, Phy. ML-HKY, Phy. ML-WAG *

Implementation • Implemented in NJTREE (or whatever) • Used in Tree. Fam and Ensembl-Compara ✤ about 20, 000 gene trees ✤ gene trees with several hundred of leaves • Website: ✤ http: //treesoft. sourceforge. net ✤ http: //www. treefam. org

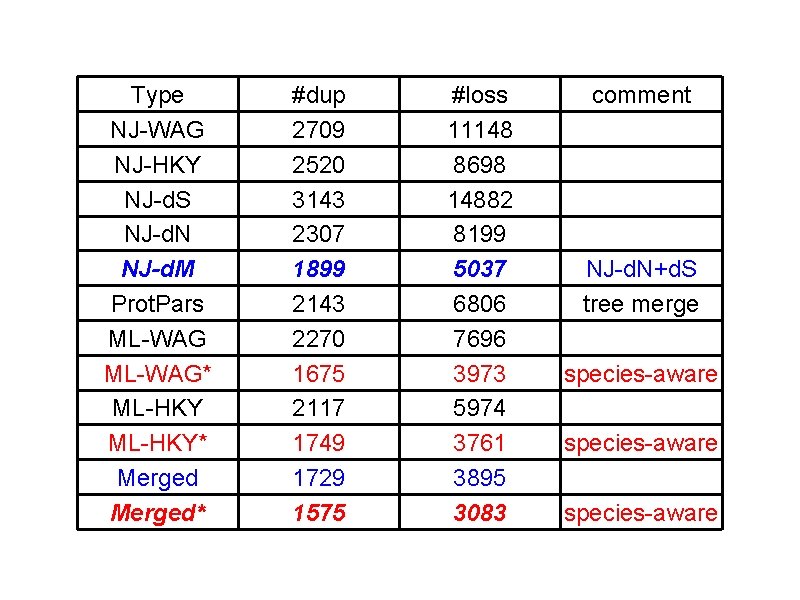
Evaluation • Data set: 197 curated gene trees from Tree. Fam ✤ 8182 internal nodes ✤ Genes mainly from vertebrates, together with worms, flies and a few plants and yeasts • Criteria: number of duplications and losses - the fewer the better

Type NJ-WAG NJ-HKY NJ-d. S NJ-d. N NJ-d. M Prot. Pars ML-WAG* ML-HKY* Merged* #dup 2709 2520 3143 2307 1899 2143 2270 1675 2117 1749 1729 1575 #loss 11148 8698 14882 8199 5037 6806 7696 3973 5974 3761 3895 3083 comment NJ-d. N+d. S tree merge species-aware

Acknowledgement • Sanger Institute ✤ Richard Durbin ✤ Avril Coghlan, Alan Moses, Jean-Karim ✤ Durbin research group • Others ✤ Lanchlan Coin ✤ Jue Ruan

Thank You!

Advanced Taxa. SCFG • CYK for parsimonious reconciliation • Inside algorithm for the probability of a gene tree P(G|S) • Inside-Outside for parameter estimation

Seq-SCFG • Rules from a known phylogenetic tree • Generate the sequences at the leaf nodes • A derivation corresponds to an assignment of ancestral sequences

Seq-SCFG Type start symbol Rule Probability S 0→(1, a) q(a) (i, a)→‹(j, b), (k, pij(b|a)pik(c|a)δi(j, i is internal c)› k) (i, a)→a i is ✤external δi(j, k)=1 iff edges (i, j) and (i, k) are present 1 in the known tree. ✤ a is a terminal symbol. For example: a∈{A, C, G, T} ✤ i is a node, internal or external

Seq-SCFG algorithms • CYK ⇒ Maximum parsimony • Inside = Felsenstein’s pruning algorithm • Inside-Outside for the posterior distribution of ancestral states and parameter est. • Extension to the previous: ✤ Felsenstein’s algorithm on multiple trees ✤ TM-WCFG is Seq-SCFG

Why gene trees? • Key to gene annotations across species • Understand gene functions • Help other evolutionary studies ✤ selection of genes ✤ intron evolution ✤ whole genome duplication • Infer species trees