Modeling Extensional Deformation of the Lithosphere Using STRCH

Modeling Extensional Deformation of the Lithosphere Using STRCH 96 – A Lagrangian Finite Element Code Dennis L. Harry Colorado State University Shelly Grandell Adams State College

Part I Description of the STRCH Algorithm

A Brief History of STRCH 96 n n STRCH developed by Dunbar & Sawyer at U. Texas in 1989 using FE solver by Becker (also at UT) STRCH 92 by Harry & Sawyer (Rice University) adds flexible boundary conditions, irregular mesh geometries, and post-processing extensions in 1992 STRCH 96 by Bowling and Harry (U. Alabama) adds cabability to include quasi-kinematic fault descriptions Extensively used for studies of continental rifting at the lithosphere-scale by the developers and colleagues (Tett, Huerta, and Grandell) to examine formation of numerous rifted continental margins and intracratonic contiental extensional provinces

The STRCH Algorithm … n Deformation controlled by modified Navier. Stokes equation for viscoplastic flow n n Flexible rheologies, including power-law creep, newtonian creep, pressure-dependant plastic failure Deformation mechanism for each element is determined dynamically => whichever has the lowest yield stress for the predicted temperature, pressure, and strain rate

The STRCH Algorithm … n Temperature controlled by transient Heat Equation Heat generation prescribed for each element n Physical properties (density, specific heat, etc. are temperature dependant) n

The Good and the Bad n Advantages n n Mesh algorithm allows for complex model parameterizations (e. g. , intrusions, terrane boundaries, etc. ) Lagrangian formulation allows for tracking of individual rock packets through time (e. g. , P-T-t history, strain history, folding of rock units) Mode of deformation is dynamically determined Disadvantages n n n Re-meshing as time progresses is a HUGE problem! Faults are included only in an ad-hoc way, and this coding effort has not proven to result in significant new understandings of processes Our treatment of isostasy is not truly dynamic

Description of Elements All 8 nodes used in 2 -D quadratic approximation of strain rate and temperature variation in each element Yellow nodes used in bilinear approximation of pressure variation in each element

Part II A Review of Previous FEM Results

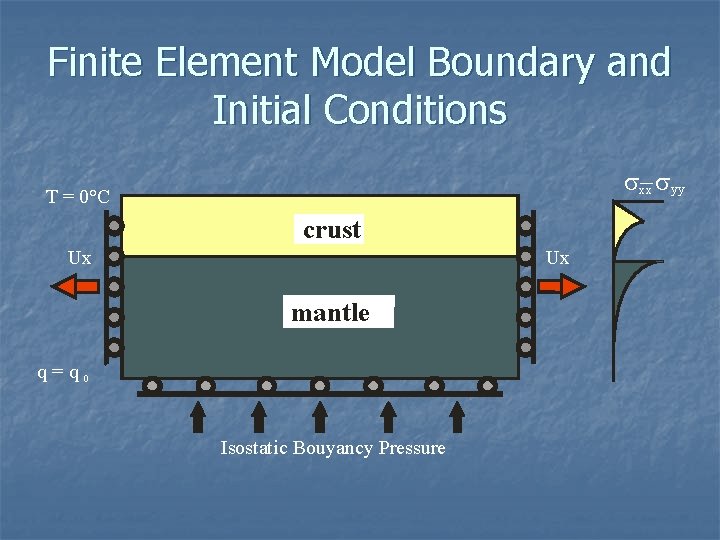
Finite Element Model Boundary and Initial Conditions s-s xx yy T = 0°C crust Ux Ux mantle q=q 0 Isostatic Bouyancy Pressure

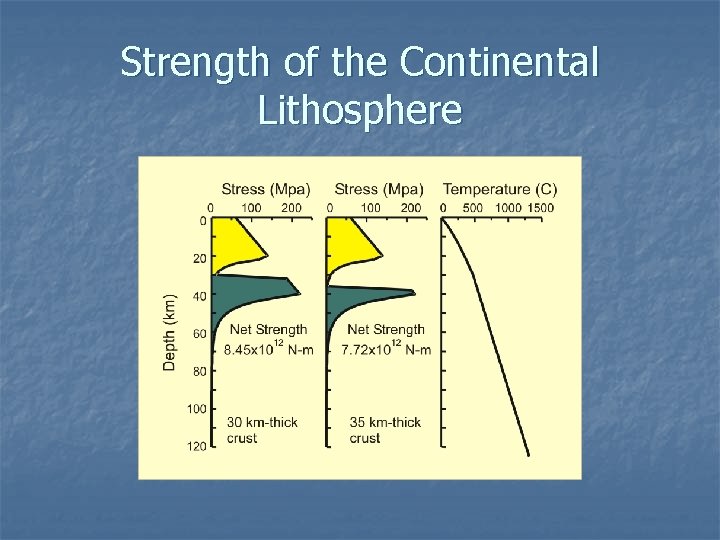
Strength of the Continental Lithosphere

Iberia: Localized Rifting Due to Mantle Weakness 0 m. y. 125 km 38 m. y. 10 mm/yr 42 m. y. 1000 km

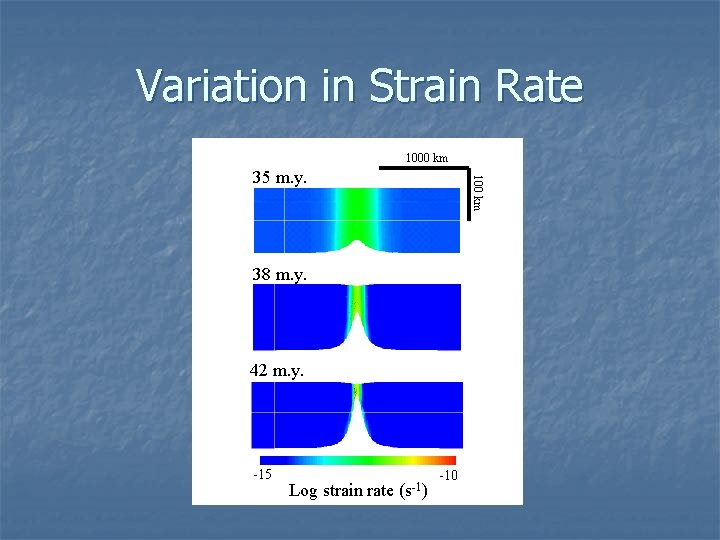
Variation in Strain Rate 1000 km 100 km 35 m. y. 38 m. y. 42 m. y. -15 Log strain rate (s-1) -10

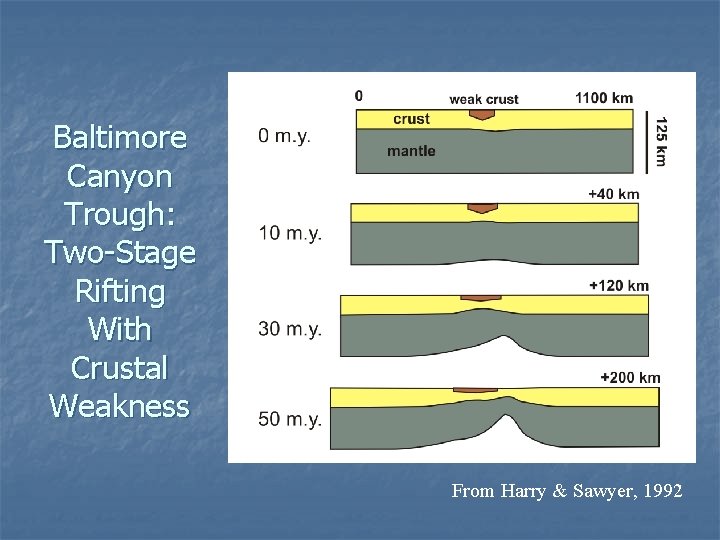
Baltimore Canyon Trough: Two-Stage Rifting With Crustal Weakness From Harry & Sawyer, 1992

Part III The Benchmarking Exercise

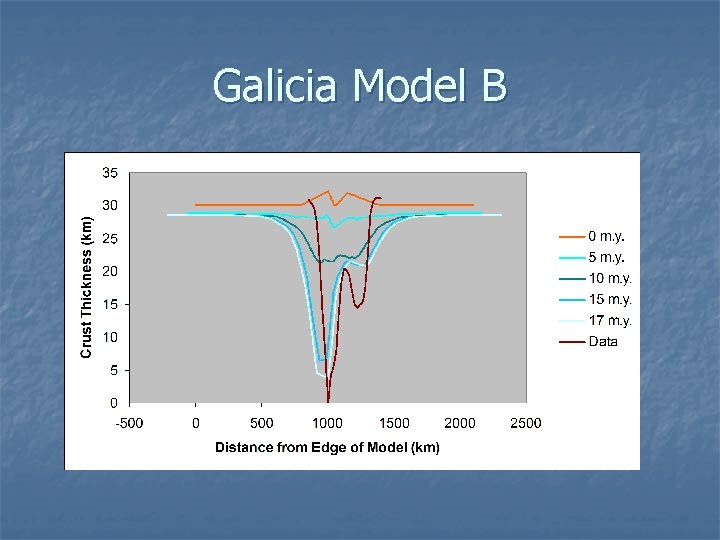
Modeling Targets n Focus on Galicia Crustal Thickness (especially Galicia Interior Basin) n Timing n Volcanism (or lack of) n Sea Floor Spreading Rate n

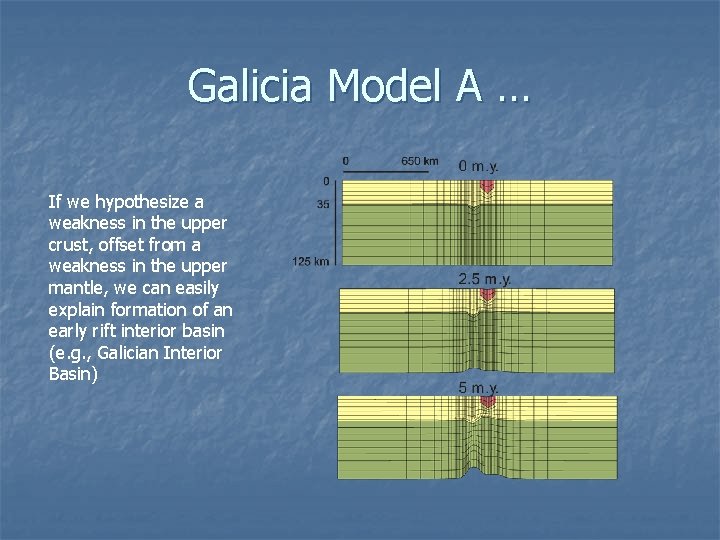
Galicia Model A … If we hypothesize a weakness in the upper crust, offset from a weakness in the upper mantle, we can easily explain formation of an early rift interior basin (e. g. , Galician Interior Basin)

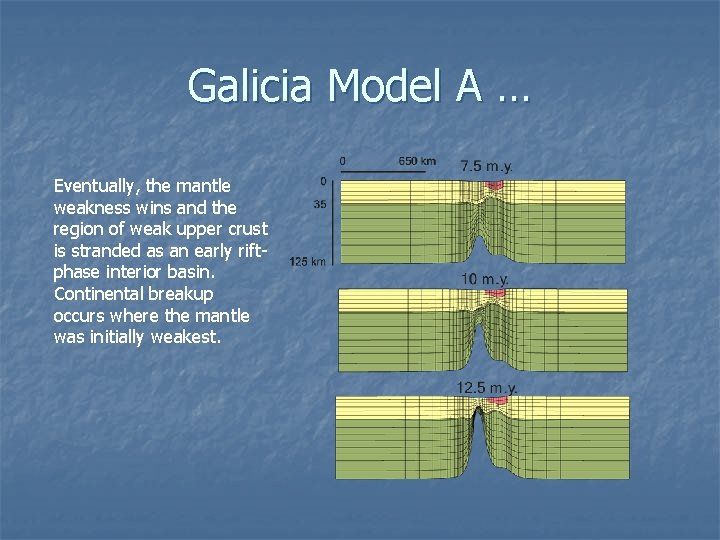
Galicia Model A … Eventually, the mantle weakness wins and the region of weak upper crust is stranded as an early riftphase interior basin. Continental breakup occurs where the mantle was initially weakest.

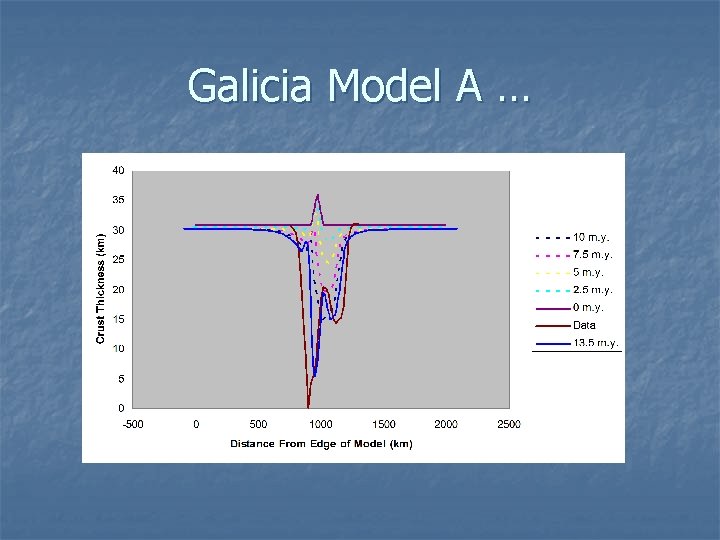
Galicia Model A …

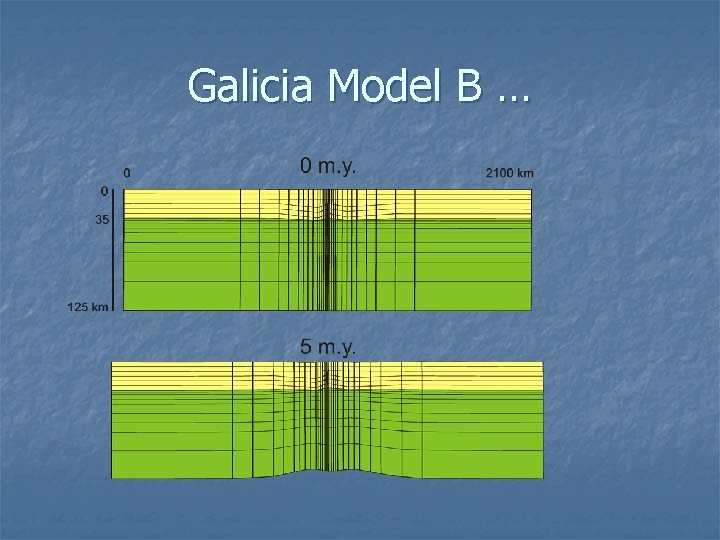
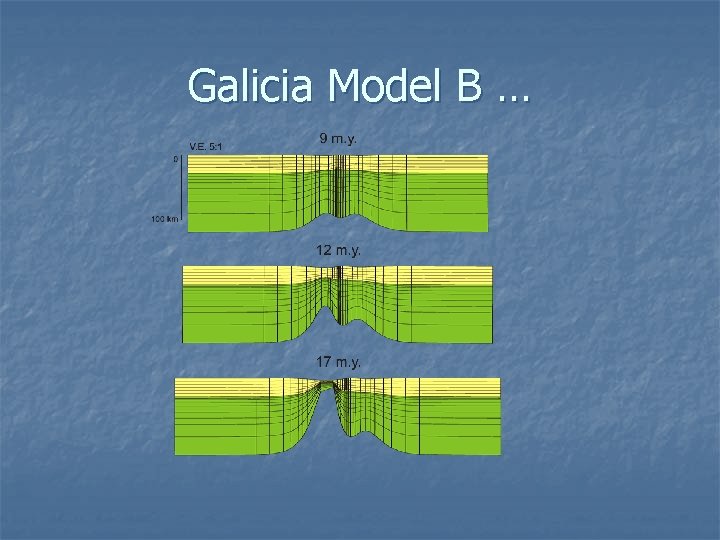
Galicia Model B …

Galicia Model B …

Galicia Model B