Modeling Discrete Variables Lecture 22 Part 1 Sections

Modeling Discrete Variables Lecture 22, Part 1 Sections 6. 4 Fri, Oct 13, 2006

Two Types of Variable Discrete variable – A variable whose set of possible values is a set of isolated points on the number line. n Continuous variable – A variable whose set of possible values is a continuous interval of real numbers. n

Example of a Discrete Variable Suppose that 10% of all households have no children, 30% have one child, 40% have two children, and 20% have three children. n Select a household at random and let X = number of children. n What is the distribution of X? n

Example of a Discrete Variable Method 1: A list. n We may list each value and its proportion. n X = 0 for 0. 10 of the population. n X = 1 for 0. 30 of the population. n X = 2 for 0. 40 of the population. n X = 3 for 0. 20 of the population. n

Example of a Discrete Variable Method 2: A table. n We may present the information as a table. n Value of X 0 1 2 3 Proportion 0. 10 0. 30 0. 40 0. 20

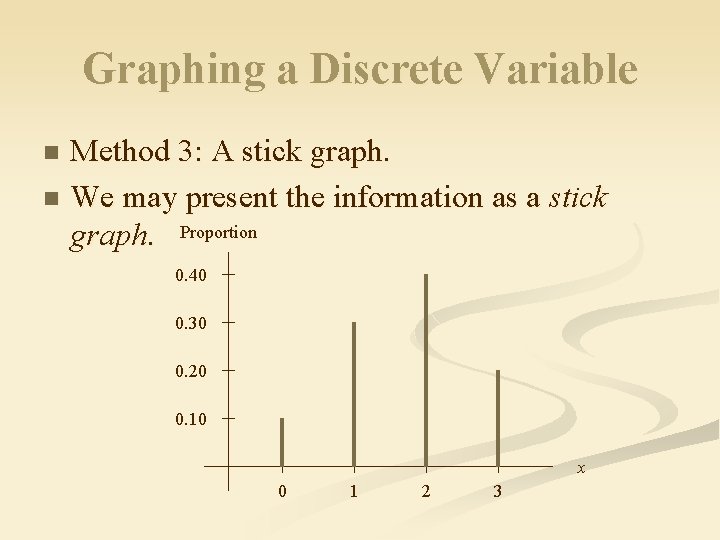
Graphing a Discrete Variable Method 3: A stick graph. n We may present the information as a stick graph. Proportion n 0. 40 0. 30 0. 20 0. 10 x 0 1 2 3

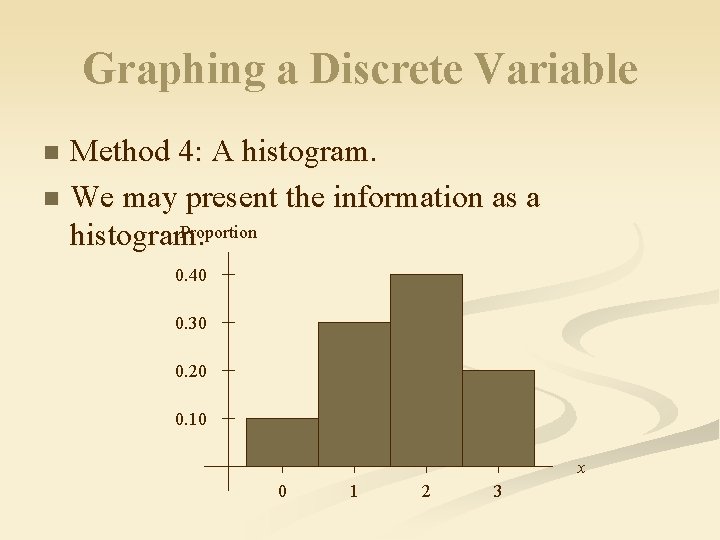
Graphing a Discrete Variable Method 4: A histogram. n We may present the information as a Proportion histogram. n 0. 40 0. 30 0. 20 0. 10 x 0 1 2 3

Discrete Random Variables Lecture 22, Part 2 Section 7. 5. 1 Fri, Oct 13, 2006

Random Variables Random variable – A variable whose value is determined by the outcome of a procedure where the outcome of at least one step in the procedure is left to chance. n Therefore, the random variable may take on a new value each time the procedure is performed, even though the procedure is exactly the same. n

Random Variables A random variable is really the same thing as the variables we studied in Chapter 2 (page 85). n A variable is a quantitative or qualitative characteristic that can be observed or measured for each member of a population. n So what makes it random? n

Examples of Random Variables Select one person at random from a group of 10 men and 20 women. n Let X be the sex of the person selected. n What are the possible values of X? n What are the probabilities of those values? n Which step of the procedure is left to chance? n

Examples of Random Variables Roll two dice. n Let X be the number of sixes that turn up. n What is the characteristic that is being observed? n What are the possible values of X? n What are the probabilities of those values? n

Examples of Random Variables Roll two dice. n Let X be the total of the two numbers. What is the characteristic that is being observed? n What are the possible values of X? n What are their probabilities? n

Examples of Random Variables A bus arrives at a bus stop every 15 minutes. You show up at a random time. n Let X be the time you wait until the bus arrives. n What are the possible values of X? n What are their probabilities? n

A Note About Probability The probability that something happens is the proportion of the time that it does happen out of all the times that it was given an opportunity to happen. n Therefore, “probability” and “proportion” are synonymous in the context of what we are doing. n

Discrete Probability Distribution Functions n Discrete Probability Distribution Function (pdf) – A function that assigns a probability to each possible value of a discrete random variable.

Rolling Two Dice Roll two dice and let X be the number of sixes. n Draw the 6 6 rectangle showing all 36 possibilities. (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) n From it we see that n P(X = 0) = 25/36. n P(X = 1) = 10/36. n P(X = 2) = 1/36. n (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)

Rolling Two Dice n We can summarize this as a list (Method 1): P(X = 0) = 25/36. n P(X = 1) = 10/36. n P(X = 2) = 1/36. n

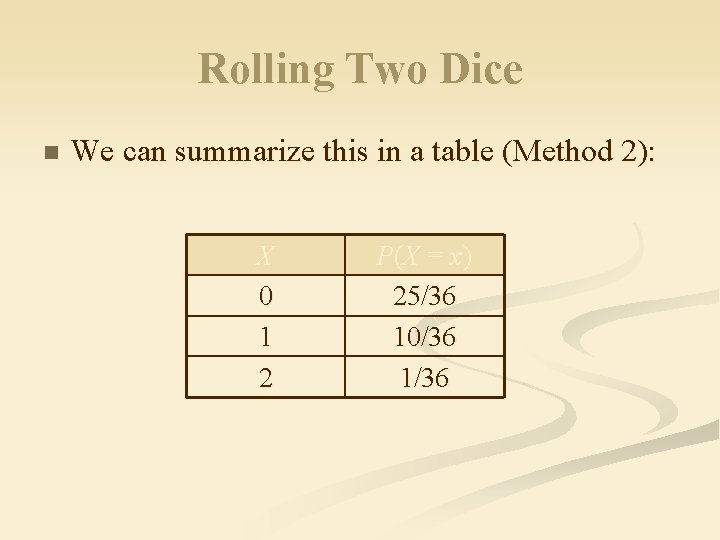
Rolling Two Dice n We can summarize this in a table (Method 2): X 0 1 2 P (X = x ) 25/36 10/36 1/36

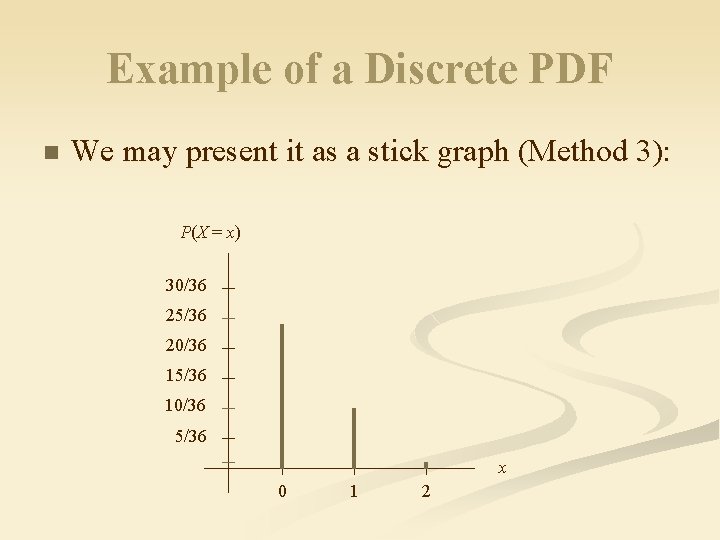
Example of a Discrete PDF n We may present it as a stick graph (Method 3): P(X = x) 30/36 25/36 20/36 15/36 10/36 5/36 x 0 1 2

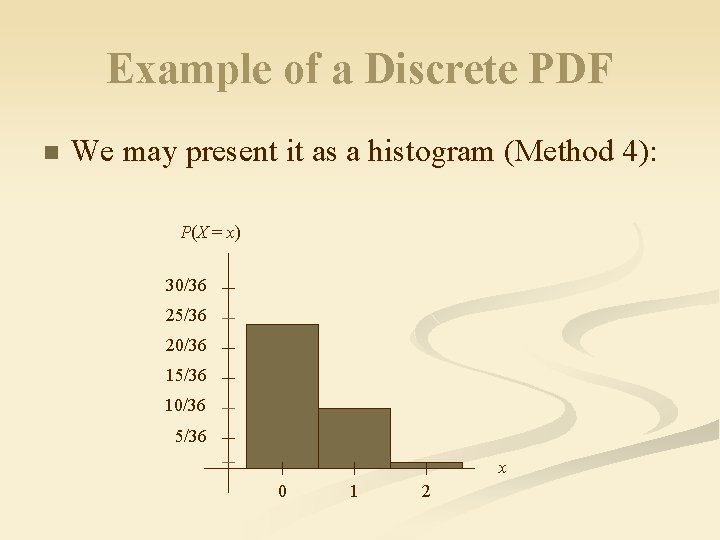
Example of a Discrete PDF n We may present it as a histogram (Method 4): P(X = x) 30/36 25/36 20/36 15/36 10/36 5/36 x 0 1 2

Rolling Two Dice Roll two dice and let X be the sum of the two numbers. n From it we see that n P(X = 2) = 1/36. n P(X = 3) = 2/36. n P(X = 4) = 3/36. n P(X = 5) = 4/36. n P(X = 6) = 5/36. n etc. n (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)

Example of a Discrete PDF Suppose that 10% of all households have no children, 30% have one child, 40% have two children, and 20% have three children. n Select a household at random and let X = number of children. n Then X is a random variable. n What is the pdf of X? n

Example of a Discrete PDF n We may present the pdf as a list. P(X = 0) = 0. 10. n P(X = 1) = 0. 30. n P(X = 2) = 0. 40. n P(X = 3) = 0. 20. n

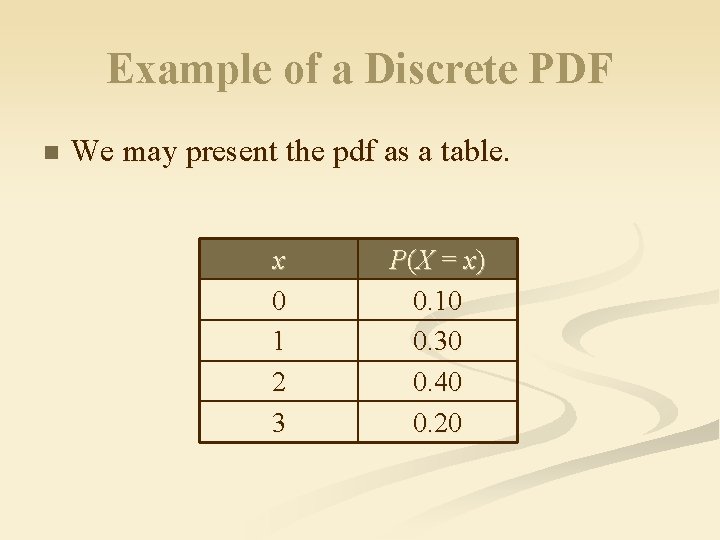
Example of a Discrete PDF n We may present the pdf as a table. x 0 1 2 3 P (X = x ) 0. 10 0. 30 0. 40 0. 20

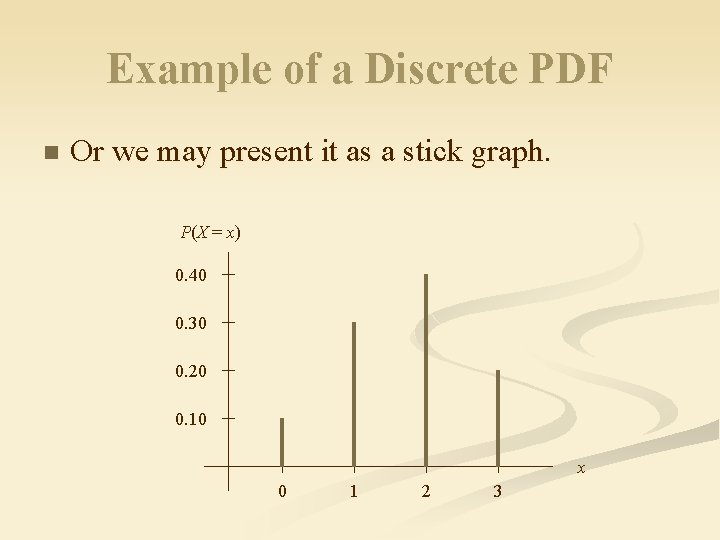
Example of a Discrete PDF n Or we may present it as a stick graph. P(X = x) 0. 40 0. 30 0. 20 0. 10 x 0 1 2 3

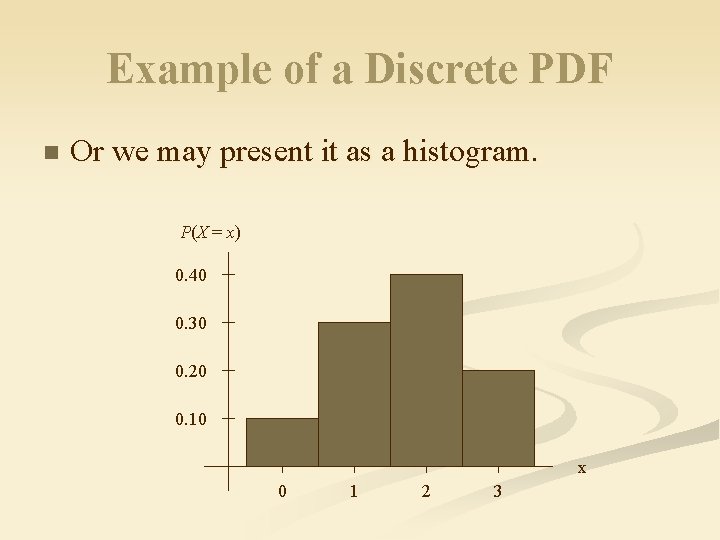
Example of a Discrete PDF n Or we may present it as a histogram. P(X = x) 0. 40 0. 30 0. 20 0. 10 x 0 1 2 3