Modeling Combinatorially Complex Ribonucleotide Reductase Tom Radivoyevitch Assistant

Modeling Combinatorially Complex Ribonucleotide Reductase Tom Radivoyevitch Assistant Professor Epidemiology and Biostatistics Case Western Reserve University Email: txr 24@case. edu Website: http: //epbi-radivot. cwru. edu/

Overview • Model enzymes as quasi-equilibria (e. g. E ES) • Combinatorially Complex Equilibria: few reactants => many possible complexes • R package: Combinatorially Complex Equilibrium Model Selection (ccems) implements methods for activity and mass data • Hypotheses: complete K = ∞ [Complex] = 0 vs binary K 1 = K 2 • Generate a set of possible models, fit them, and select the best • Model Selection: Akaike Information Criterion (AIC) • AIC decreases with P and then increases • Billions of models, but only thousands near AIC upturn • Generate 1 P, 2 P, 3 P model space chunks sequentially • Use structures to constrain complexity and simplicity of models

Ultimate Goal • Better understanding => better control • Conceptual models help trial designs today • Computer models of airplanes help train pilots and autopilots Present • • Future Safer flying airplanes with autopilots Ultimate Goal: individualized, state feedback based clinical trials Radivoyevitch et al. (2006) BMC Cancer 6: 104

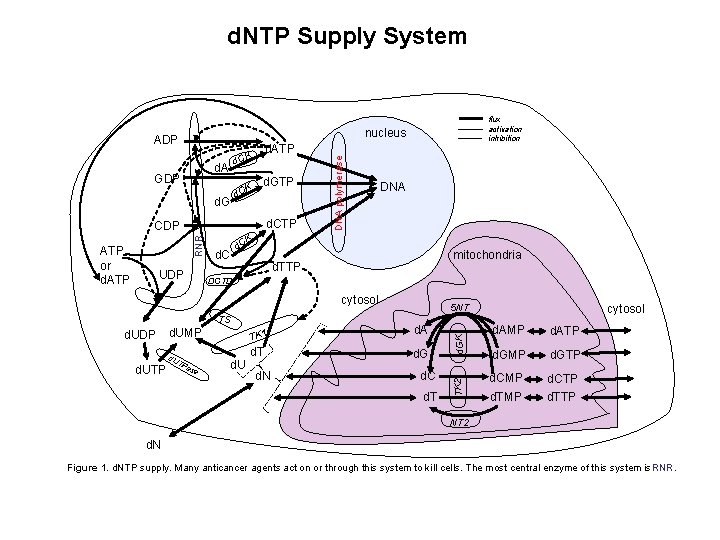
d. NTP Supply System nucleus ADP K d. C d. GTP d. CTP CK d d. C mitochondria d. TTP DCTD cytosol TS d. UDP d. UTP d. UMP d. U T Pa se d. U TK 1 d. A d. T d. G d. N cytosol 5 NT d. C d. T d. GK UDP DNA TK 2 RNR CDP DNA polymerase d. ATP K d. C d. A GDP ATP or d. ATP flux activation inhibition d. AMP d. ATP d. GMP d. GTP d. CMP d. CTP d. TMP d. TTP NT 2 d. N Figure 1. d. NTP supply. Many anticancer agents act on or through this system to kill cells. The most central enzyme of this system is RNR.

Ribonucleotide Reductase (RNR) ATP activates at hexamerization site? ? d. ATP inhibits at activity site, ATP activates at activity site? R 1 R 1 R 2 R 1 5 catalytic site states x 5 s-site states x 3 a-site states x 2 h-site states = 150 states Þ (150)6 different hexamer complexes => 2^(150)6 models 2^(150) 6 = ~1 followed by a trillion zeros 1 trillion complexes => 1 trillion (1 followed by only 12 zeros) 1 -parameter models RNR is Combinatorially Complex R 1 R 1 R 2 R 2 R 1 UDP, CDP, GDP, ADP bind to catalytic site R 1 ATP, d. TTP, d. GTP bind to selectivity site R 1

Michaelis-Menten Model E+S but ES so Key perspective RNR: no NDP and no R 2 dimer => kcat of complex is zero, else different R 1 -R 2 -NDP complexes can have different kcat values.

Michaelis-Menten Model [S] vs. [ST] Substitute this in here to get a quadratic in [S] whose solution is Bigger systems of higher polynomials cannot be solved algebraically => use ODEs (above) (3) R=R 1 G=GDP r=R 22 t=d. TTP solid line = Eqs. (1 -2) dotted = Eq. (3) Data from Scott, C. P. , Kashlan, O. B. , Lear, J. D. , and Cooperman, B. S. (2001) Biochemistry 40(6), 1651 -166

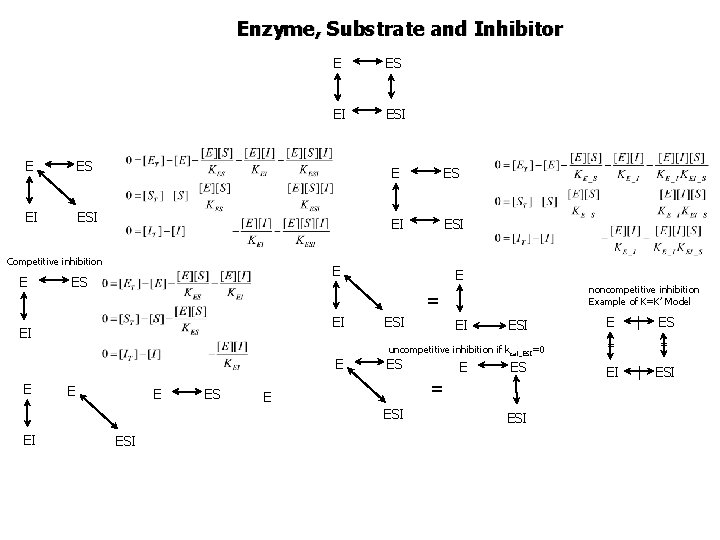
Enzyme, Substrate and Inhibitor E ES EI ESI Competitive inhibition E E ES EI E ES ESI EI ESI uncompetitive inhibition if kcat_ESI=0 ES E ES = E ESI EI noncompetitive inhibition Example of K=K’ Model = EI E E ESI E = EI | ES = | ESI

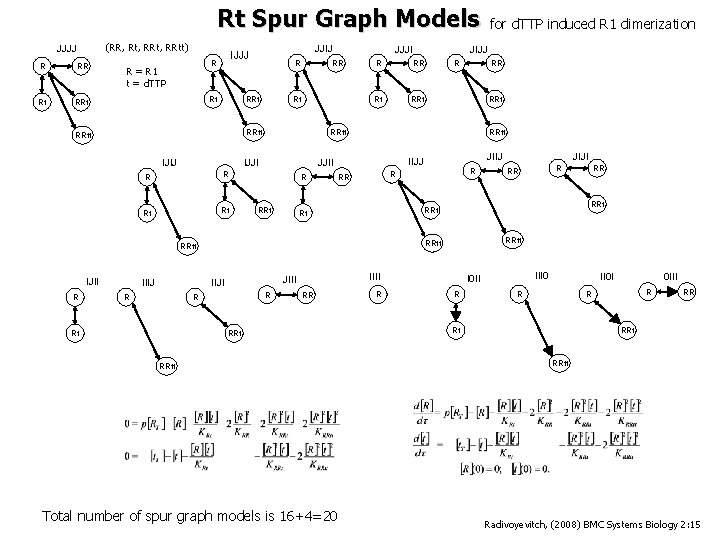
Rt Spur Graph Models (RR, Rt, RRtt) JJJJ R Rt RRt R R = R 1 t = d. TTP JJIJ IJJJ Rt R RRt Rt RRtt IJIJ R Rt RR Rt RRt R IIIJ R RRt JIIJ R R RR RRtt Total number of spur graph models is 16+4=20 RR R RR RRtt IIII JIJI R RRt Rt RRtt R Rt RR RRt IIJJ JJII IIJI R R RRtt IJII JIJJ R RRtt IJJI R JJJI RR for d. TTP induced R 1 dimerization III 0 I 0 II R II 0 I R 0 III R R Rt RR RRtt Radivoyevitch, (2008) BMC Systems Biology 2: 15

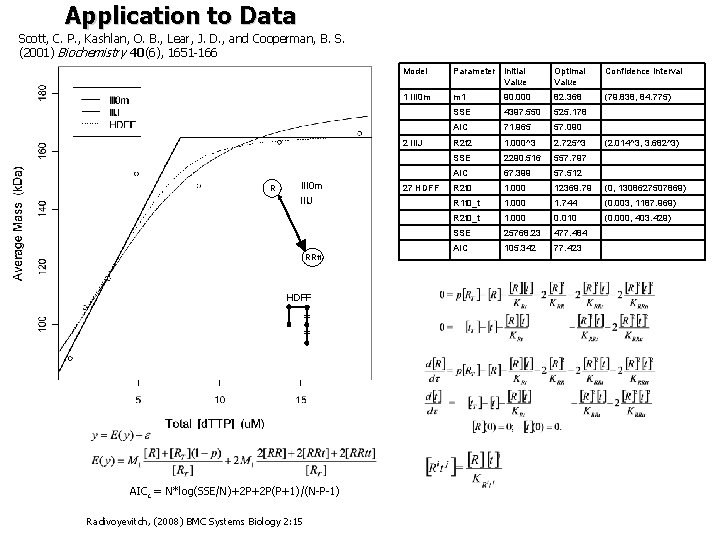
Application to Data Scott, C. P. , Kashlan, O. B. , Lear, J. D. , and Cooperman, B. S. (2001) Biochemistry 40(6), 1651 -166 R Model Parameter Initial Value Optimal Value Confidence Interval 1 III 0 m m 1 90. 000 82. 368 (79. 838, 84. 775) SSE 4397. 550 525. 178 AIC 71. 965 57. 090 2 IIIJ R 2 t 2 1. 000^3 2. 725^3 SSE 2290. 516 557. 797 AIC 67. 399 57. 512 III 0 m 27 HDFF R 2 t 0 1. 000 12369. 79 (0, 1308627507869) IIIJ R 1 t 0_t 1. 000 1. 744 (0. 003, 1187. 969) R 2 t 0_t 1. 000 0. 010 (0. 000, 403. 429) SSE 25768. 23 477. 484 AIC 105. 342 77. 423 RRtt HDFF = = AICc = N*log(SSE/N)+2 P+2 P(P+1)/(N-P-1) Radivoyevitch, (2008) BMC Systems Biology 2: 15 (2. 014^3, 3. 682^3)

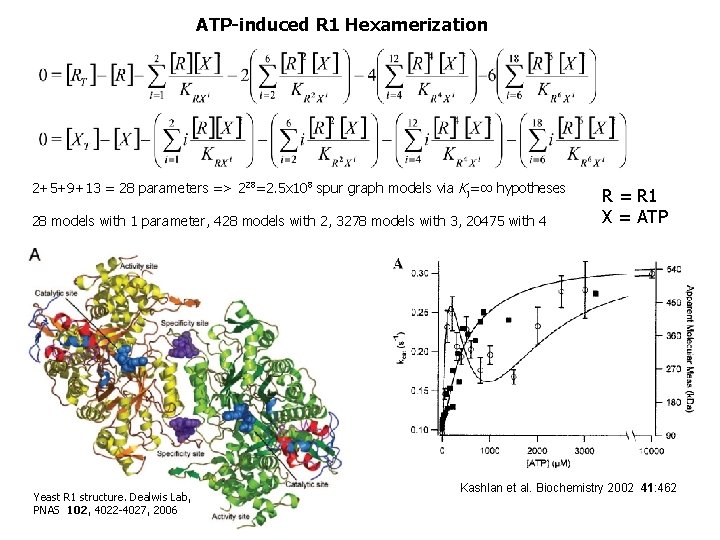
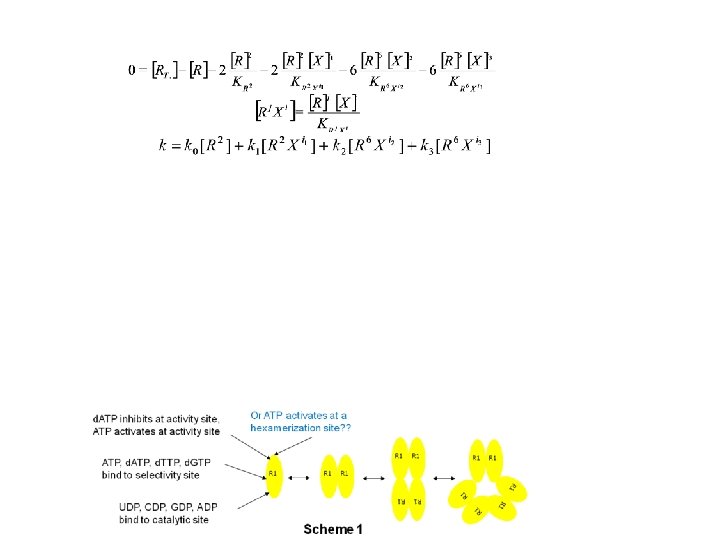
ATP-induced R 1 Hexamerization 2+5+9+13 = 28 parameters => 228=2. 5 x 108 spur graph models via Kj=∞ hypotheses 28 models with 1 parameter, 428 models with 2, 3278 models with 3, 20475 with 4 Yeast R 1 structure. Dealwis Lab, PNAS 102, 4022 -4027, 2006 R = R 1 X = ATP Kashlan et al. Biochemistry 2002 41: 462

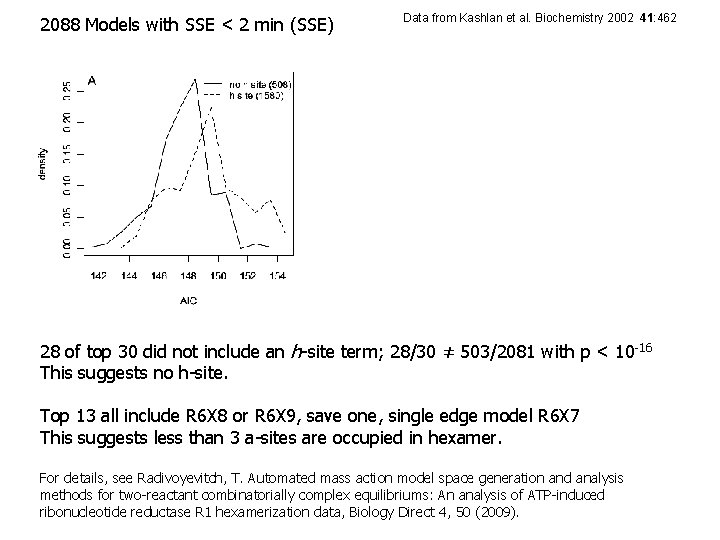
2088 Models with SSE < 2 min (SSE) Data from Kashlan et al. Biochemistry 2002 41: 462 28 of top 30 did not include an h-site term; 28/30 ≠ 503/2081 with p < 10 -16 This suggests no h-site. Top 13 all include R 6 X 8 or R 6 X 9, save one, single edge model R 6 X 7 This suggests less than 3 a-sites are occupied in hexamer. For details, see Radivoyevitch, T. Automated mass action model space generation and analysis methods for two-reactant combinatorially complex equilibriums: An analysis of ATP-induced ribonucleotide reductase R 1 hexamerization data, Biology Direct 4, 50 (2009).

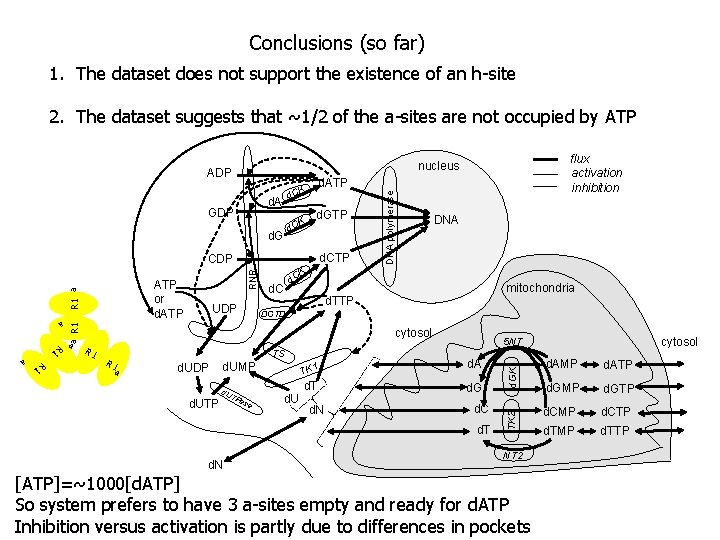
Conclusions (so far) 1. The dataset does not support the existence of an h-site 2. The dataset suggests that ~1/2 of the a-sites are not occupied by ATP ADP K d. C d. GTP d. C a mitochondria d. TTP DCTD cytosol R 1 a TS d. UDP a R 1 a d. UTP d. UMP d. U T Pa se d. U TK 1 d. A d. T d. G d. N d. C d. T d. N cytosol 5 NT d. GK R 1 a K d. C a R 1 UDP DNA TK 2 RNR CDP DNA polymerase d. ATP K d. C d. A GDP ATP or d. ATP flux activation inhibition nucleus NT 2 [ATP]=~1000[d. ATP] So system prefers to have 3 a-sites empty and ready for d. ATP Inhibition versus activation is partly due to differences in pockets d. AMP d. ATP d. GMP d. GTP d. CMP d. CTP d. TMP d. TTP

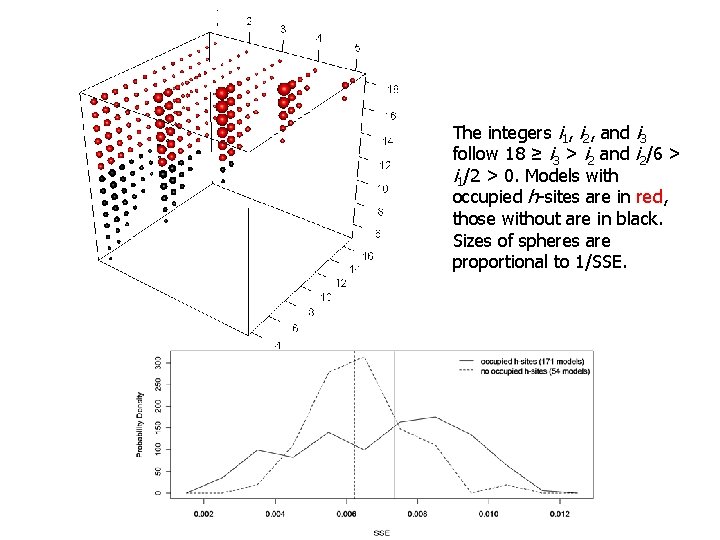
The integers i 1, i 2, and i 3 follow 18 ≥ i 3 > i 2 and i 2/6 > i 1/2 > 0. Models with occupied h-sites are in red, those without are in black. Sizes of spheres are proportional to 1/SSE.

SUMMARY Combinatorially Complex Equilibrium Model Selection (ccems, CRAN 2009) Model individual enzymes R 1 R 1 Model networks of enzymes R 1 R 1 R 2 R 2 R 1 R 1 R 1 R 2 Systems Biology Markup Language interface to R (SBMLR, BIOC 2004)

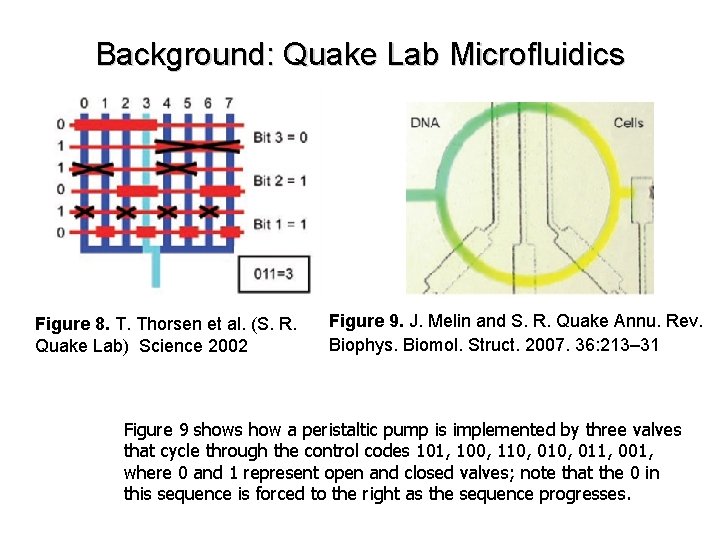
Background: Quake Lab Microfluidics Figure 8. T. Thorsen et al. (S. R. Quake Lab) Science 2002 Figure 9. J. Melin and S. R. Quake Annu. Rev. Biophys. Biomol. Struct. 2007. 36: 213– 31 Figure 9 shows how a peristaltic pump is implemented by three valves that cycle through the control codes 101, 100, 110, 011, 001, where 0 and 1 represent open and closed valves; note that the 0 in this sequence is forced to the right as the sequence progresses.

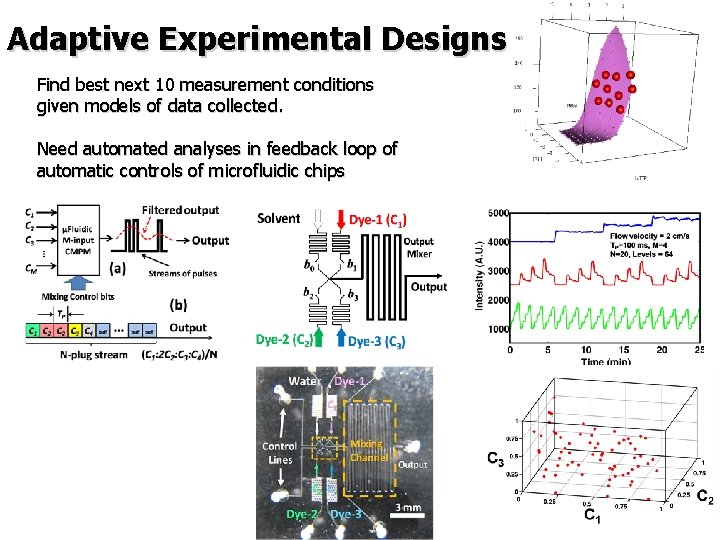
Adaptive Experimental Designs Find best next 10 measurement conditions given models of data collected. Need automated analyses in feedback loop of automatic controls of microfluidic chips

Why Systems Biology Model components: (Deterministic = signal) + (Stochastic = noise) Statistics Engineering Emphasis is on the stochastic component of the model. Emphasis is on the deterministic component of the model Is there something in the black box or are the input wires disconnected from the output wires such that only thermal noise is being measured? We already know what is in the box, since we built it. The goal is to understand it well enough to be able to control it. Do we have enough data? Predict the best multi-agent drug dose time course schedules Increasing amounts of data/knowledge

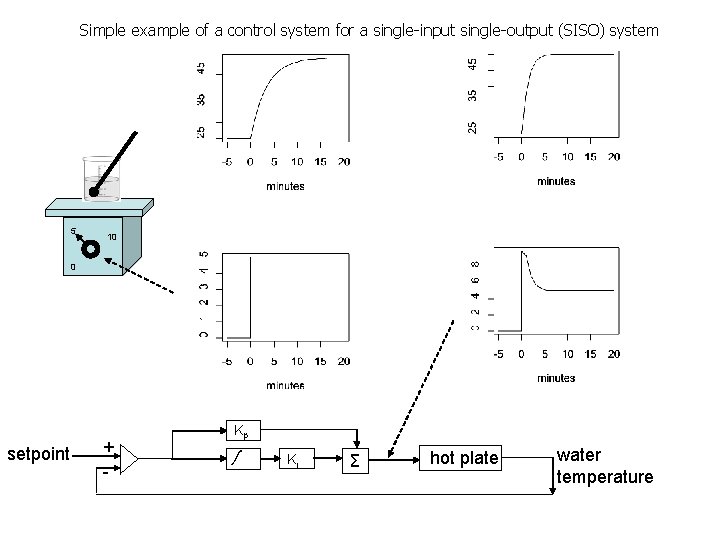
Simple example of a control system for a single-input single-output (SISO) system 5 10 0 setpoint + - Kp ∫ Ki Σ hot plate water temperature

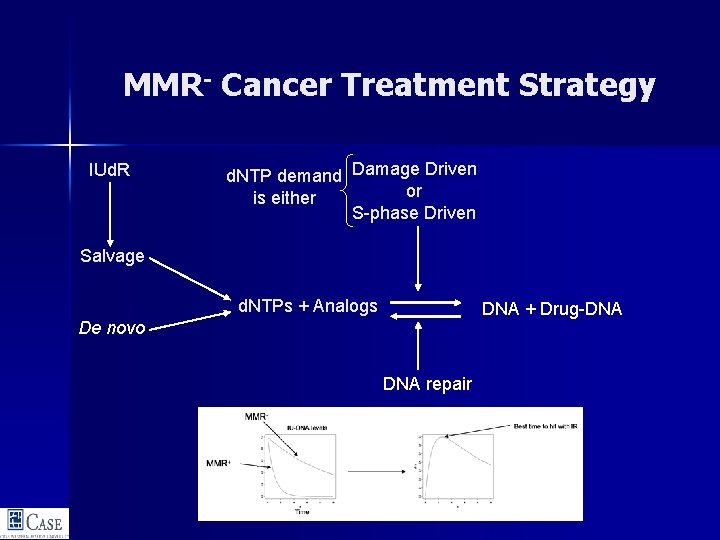
MMR- Cancer Treatment Strategy IUd. R d. NTP demand Damage Driven or is either S-phase Driven Salvage d. NTPs + Analogs DNA + Drug-DNA De novo DNA repair

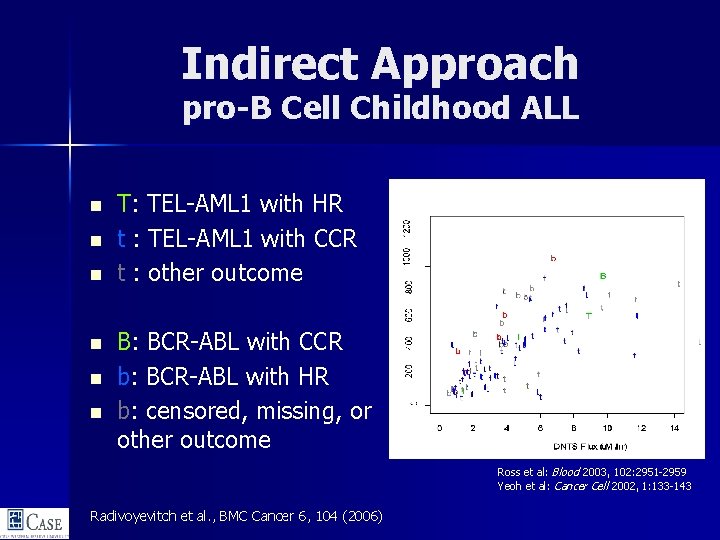
Indirect Approach pro-B Cell Childhood ALL n n n T: TEL-AML 1 with HR t : TEL-AML 1 with CCR t : other outcome B: BCR-ABL with CCR b: BCR-ABL with HR b: censored, missing, or other outcome Ross et al: Blood 2003, 102: 2951 -2959 Yeoh et al: Cancer Cell 2002, 1: 133 -143 Radivoyevitch et al. , BMC Cancer 6, 104 (2006)

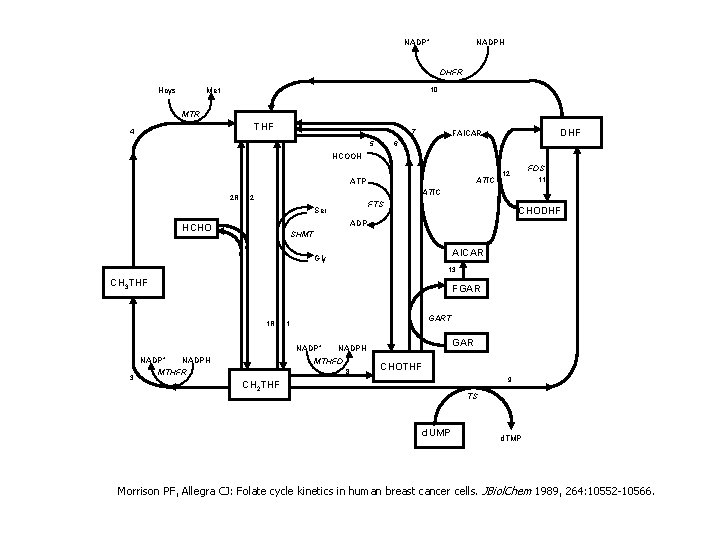
NADP+ NADPH DHFR Hcys 10 Met MTR THF 4 7 5 DHF FAICAR 6 HCOOH ATIC ATP 2 R FDS 12 11 ATIC 2 FTS Ser CHODHF ADP HCHO SHMT AICAR Gly 13 CH 3 THF FGAR 1 R GART 1 NADP+ 3 NADP+ NADPH MTHFR GAR NADPH MTHFD 8 CHOTHF 9 CH 2 THF TS d. UMP d. TMP Morrison PF, Allegra CJ: Folate cycle kinetics in human breast cancer cells. JBiol. Chem 1989, 264: 10552 -10566.

Conclusions n For systems biology to succeed: – move biological research toward systems which are best understood – specialize modelers to become experts in biological literatures (e. g. d. NTP Supply) n Systems biology is not a service

Acknowledgements n n n n Case Comprehensive Cancer Center NIH (K 25 CA 104791) Charles Kunos (CWRU) John Pink (CWRU) Chris Dealwis (CWRU) Anders Hofer (Umea) Yun Yen (COH) And thank you for listening!

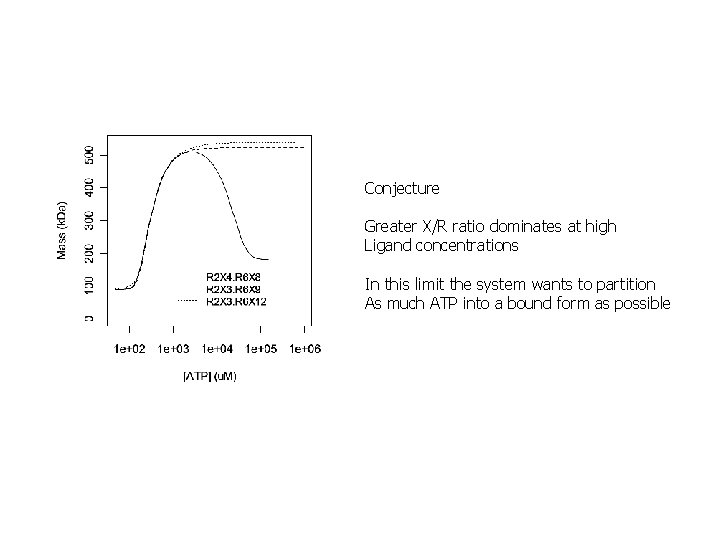
Conjecture Greater X/R ratio dominates at high Ligand concentrations In this limit the system wants to partition As much ATP into a bound form as possible

library(ccems) # Ribonucleotide Reductase Example topology <- list( heads=c("R 1 X 0", "R 2 X 2", "R 4 X 4", "R 6 X 6"), sites=list( # s-sites are already filled only in (j>1)-mers a=list( #a-site thread m=c("R 1 X 1"), # monomer 1 d=c("R 2 X 3", "R 2 X 4"), # dimer 2 t=c("R 4 X 5", "R 4 X 6", "R 4 X 7", "R 4 X 8"), # tetramer 3 h=c("R 6 X 7", "R 6 X 8", "R 6 X 9", "R 6 X 10", "R 6 X 11", "R 6 X 12") # hexamer 4 ), # tails of a-site threads are heads of h-site threads h=list( # h-site m=c("R 1 X 2"), # monomer 5 d=c("R 2 X 5", "R 2 X 6"), # dimer 6 t=c("R 4 X 9", "R 4 X 10", "R 4 X 11", "R 4 X 12"), # tetramer 7 h=c("R 6 X 13", "R 6 X 14", "R 6 X 15", "R 6 X 16", "R 6 X 17", "R 6 X 18")# hexamer 8 ) ) ) g=mkg(topology, TCC=TRUE) dd=subset(RNR, (year==2002)&(fg==1)&(X>0), select=c(R, X, m, year)) cpus. Per. Host=c("localhost" = 4, "compute-0 -0"=4, "compute-0 -1"=4, "compute-0 -2"=4) top 10=ems(dd, g, cpus. Per. Host=cpus. Per. Host, max. Total. Ps=3, ptype="SOCK", KIC=100)

Comments on Methods