Modeling Capital Markets with Financial Signal processing Bridging

Modeling Capital Markets with Financial Signal processing Bridging Technical Analysis & Stochastic-Process Modeling (I) 調和財務 程部, Harmonic Financial Engineering 騰網知識科技開發

a step toward Rational Memory Process Canonical Foundation of Financial Engineering by Sifeon

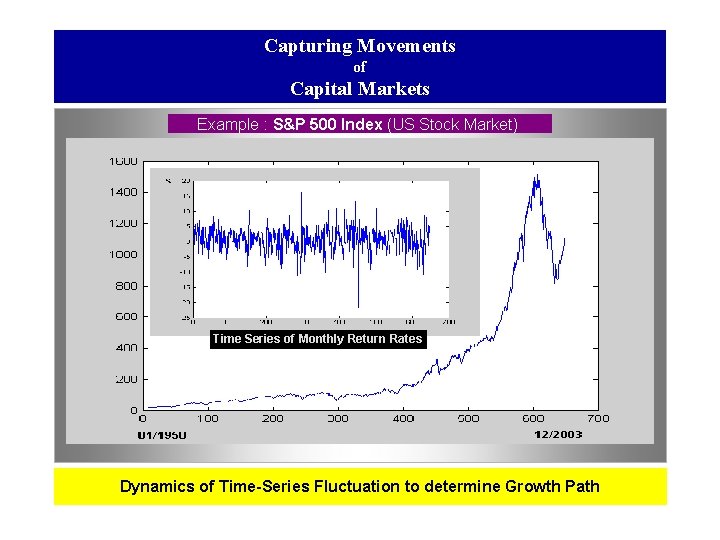
Capturing Movements of Capital Markets Example : S&P 500 Index (US Stock Market) Time Series of Monthly Return Rates Dynamics of Time-Series Fluctuation to determine Growth Path

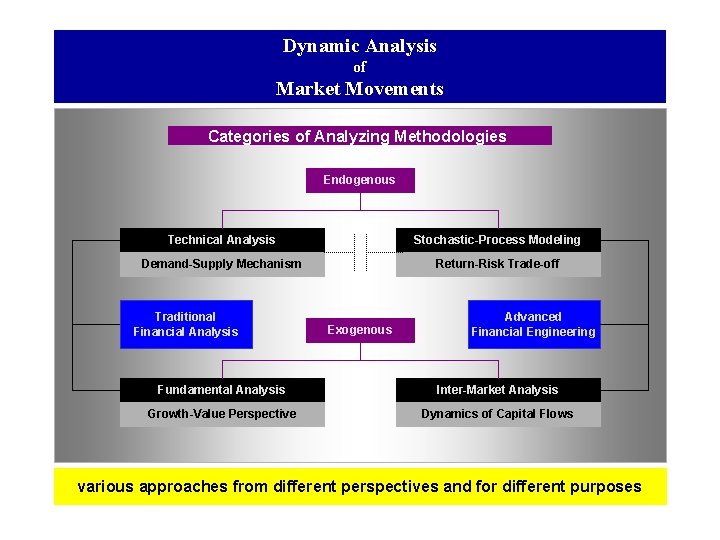
Dynamic Analysis of Market Movements Categories of Analyzing Methodologies Endogenous Technical Analysis Stochastic-Process Modeling Demand-Supply Mechanism Return-Risk Trade-off Traditional Financial Analysis Exogenous Advanced Financial Engineering Fundamental Analysis Inter-Market Analysis Growth-Value Perspective Dynamics of Capital Flows various approaches from different perspectives and for different purposes

Part I Elementary Ideas in Technical Analysis naïve financial signal processing

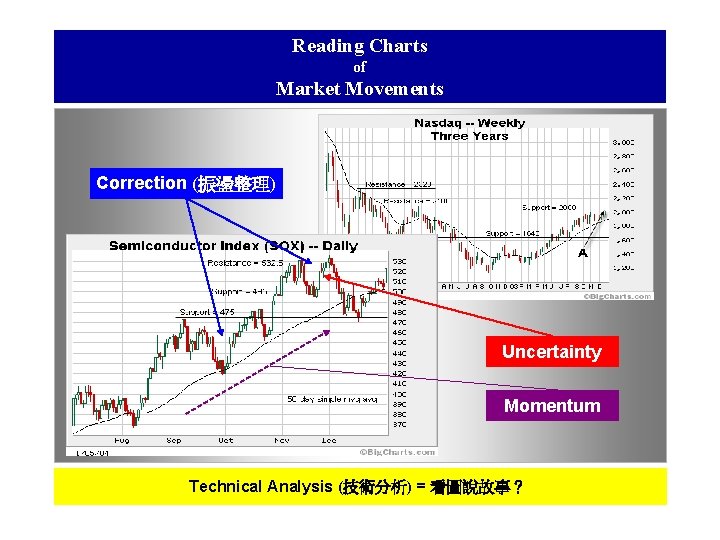
Reading Charts of Market Movements Correction (振盪整理) Uncertainty Momentum Technical Analysis (技術分析) = 看圖說故事？

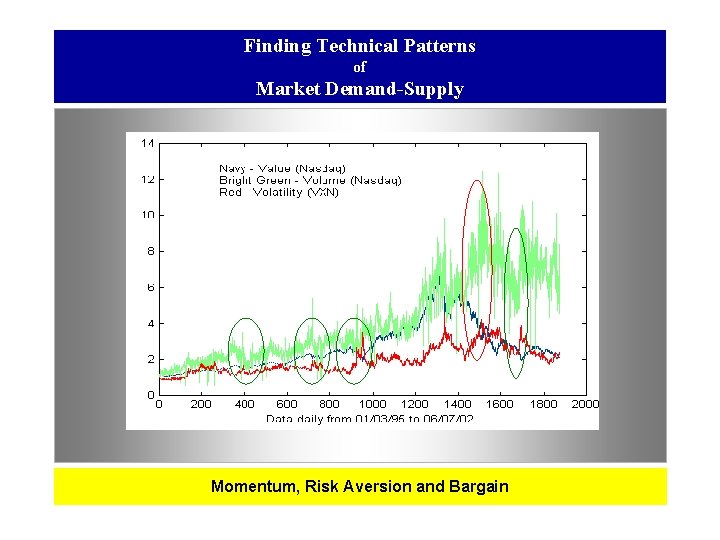
Finding Technical Patterns of Market Demand-Supply Momentum, Risk Aversion and Bargain

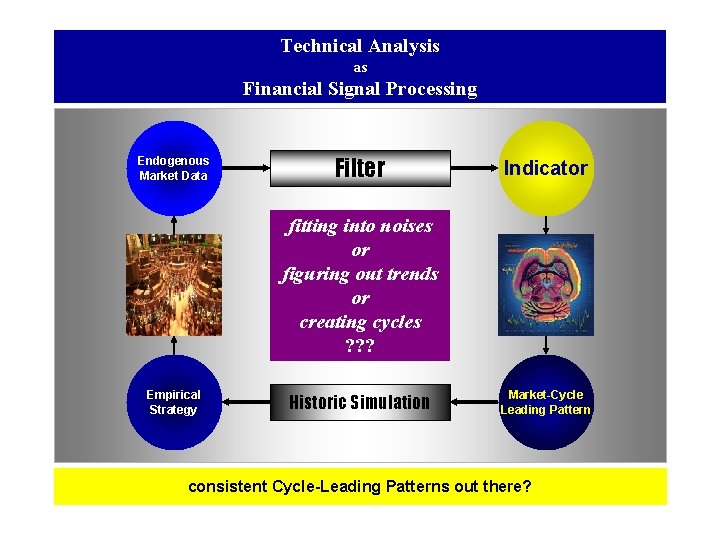
Technical Analysis as Financial Signal Processing Endogenous Market Data Filter Indicator fitting into noises or figuring out trends or creating cycles ? ? ? Empirical Strategy Historic Simulation Market-Cycle Leading Pattern consistent Cycle-Leading Patterns out there?

Strength and Weakness of Technical Analysis • Strength – Observation & Explanation about Dynamic Phenomena trying to explain filtered patterns based on market demand-supply mechanism driven by market sentiment e. g. Moving Average (EMA, MACD), Relative Strength Index, Money Flow Index, Bollinger Bands, Support and Resistance Levels, • Weakness – Formulation & Correction about Dynamic Structure lack of probabilistic formulation for consistent strategy construction by risk-return trade-off and systematic performance assessment be aware of noisy illusions!

Part II Fundamental Structures in Stochastic-Process Modeling naïve capital market modeling

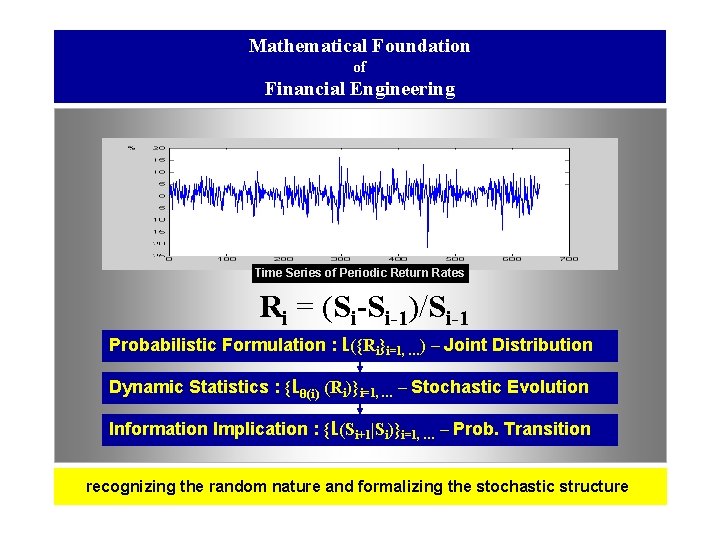
Mathematical Foundation of Financial Engineering Time Series of Periodic Return Rates Ri = (Si-Si-1)/Si-1 Probabilistic Formulation : L({Ri}i=1, …) – Joint Distribution Dynamic Statistics : {Lθ(i) (Ri)}i=1, … – Stochastic Evolution Information Implication : {L(Si+1|Si)}i=1, … – Prob. Transition recognizing the random nature and formalizing the stochastic structure

Academic Canonical Frameworks of Capital Market Modeling Discrete-Time Version (Auto-Regression) Continuous-Time Version (Stochastic Differential Equation) I. I. D. Normal Sequence Geometric Brownian Motion Ri = μ+σ·εi, εi ~ N(0, 1) d. St/St = r·dt + s·d. Wt GARCH SVM (Mean-Reverting Process) Ri = μ+σi·εi, εi ~ N(0, 1) σi 2 = α 0+Σpj=1αj εi-j 2 +Σqj=1βj σ i-j 2 d. St/St = r·dt + |Vt|·d. Wt d. Vt = -k·(Vt-c)·dt + f(Vt)·d. Zt Generalization Ri = μ(Ri-1, Ri-2, …)+σ (Ri-1, Ri-2, …) ·εi d. St/St = Mt·dt + Vt·d. Wt could the models borrowed from physical systems well approach econ ones?

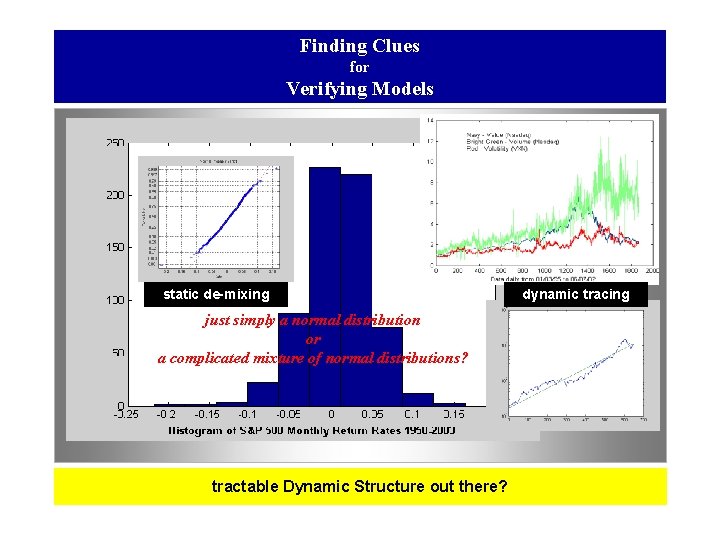
Finding Clues for Verifying Models static de-mixing just simply a normal distribution or a complicated mixture of normal distributions? tractable Dynamic Structure out there? dynamic tracing

Strength and Weakness of Stochastic-Process Modeling • Strength – Formulation & Correction about Dynamic Structure strong probabilistic formulation for consistent strategy construction by risk-return trade-off and systematic risk management (tools & paradigms by financial engineering) • Weakness – Observation & Explanation about Dynamic Phenomena Ignoring (if any) “cyclic phenomena” and “investment paradigms” due to market demand-supply mechanism driven by market sentiment and rationality be aware of simple biases!

Part III Reality & Lessons it’s a jungle out there

The Complex Reality for Thoughts • Capital Markets are Complex Dynamic Systems • Non-linear Dynamic Mechanism • Non-stationary Evolution due to changing Econ Conditions and Investment Paradigms • Multi-Component Framework of Market Behavior • Trend – Change Points, Long-Term Evolutionary Structural Changes • Seasonality – Periodic Factors • Cycles – Dynamic Swings around Equilibrium • Shocks – Unpredictable Impacts • Noises – Endogenous and Environmental Uncertainties • Diversification in Market Constitution • Sentiment – Individual Investors • Rationality – Institutional Investors (Smart Money) • Strategy – Arbitrageurs, Risk Hedgers can ? ? GARCH deal with it ? ? ? • Multi-Channel Infrastructure of Money Flows • Swifter and Swifter Trading Systems • Broader and Broader Asset Categories • More Sophisticated and Complicated Financial Products and Trading Schemes • Reflexivity too many factors affecting market movements to figure out? !

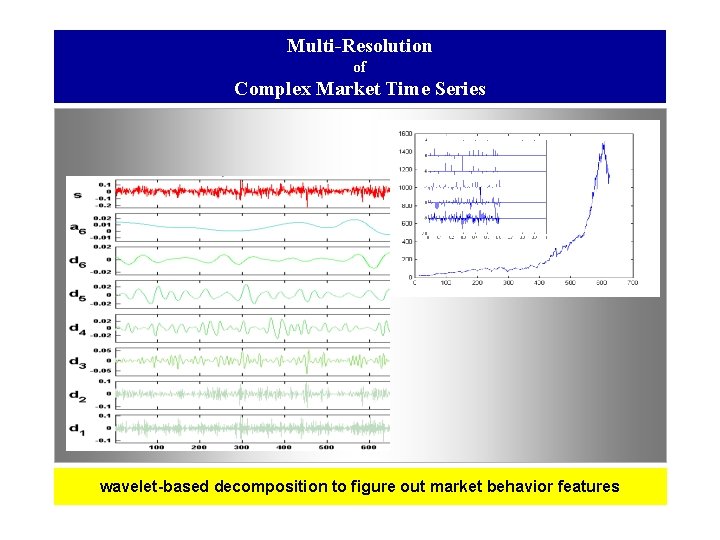
Multi-Resolution of Complex Market Time Series wavelet-based decomposition to figure out market behavior features

Hard Lessons from Markets v 1974 Great Stock Market Capitulation v 1987 Great Stock Market Crash v 1989 Nikkei Bubble Burst v 1997 Asian Currency Crisis v 1998 LTCM Fallout v 2000 Nasdaq (Tech) Bubble Burst dynamic risks beyond interpretation of stochastic volatility (no anomaly talk)

Part IV Rational Memory Processes a canonical methodological framework of capital market modeling based on financial signal processing

Prospects for Modeling Capital Markets • Theoretical Issues (about mathematical analysis) • Dynamics – Demand Supply Mechanism • Randomness – Uncertainty Structure (multi-scale noise structure) • Practical Issues (about paradigms) • Market Sentiment – Momentum, Uncertainty • Market Rationality – Prediction, Risk-Return Trade-Off • Market Strategy – Arbitrage, Risk Hedging Schemes • Market Efficiency & Completeness – Financial Infrastructures, Products • Market Liquidity & Friction – Trading Volumes, Cost, Turn-Over rate • Market Constitution – Economical, Cultural, Geopolitical Backgrounds • Technical Issues (about applications and implications) • Model Identification – Parameter Estimation • Model Assessment – Modeling Risk (Modeling Bias, Estimation Loss) • Model Adaptation – Coefficient Relations to Econ and Other Markets’ Conditions • Model Extensibility – Extension to Absorb New Factors counting for “Anomalies” setting a modeling methodological framework to incorporate the prospects

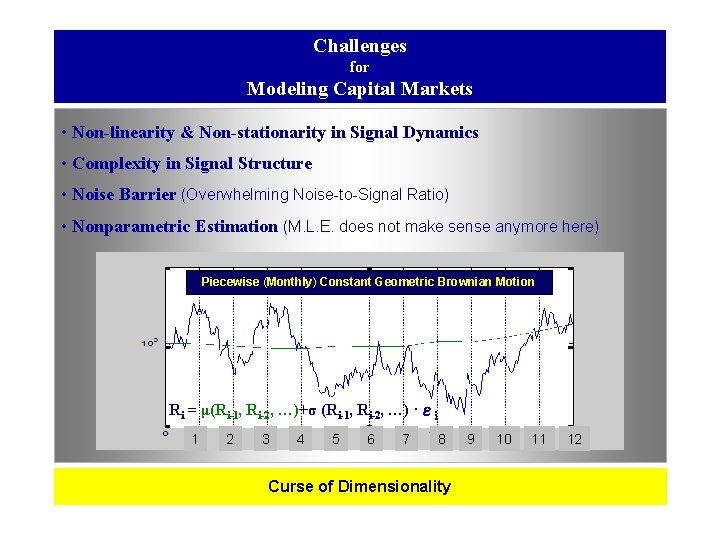
Challenges for Modeling Capital Markets • Non-linearity & Non-stationarity in Signal Dynamics • Complexity in Signal Structure • Noise Barrier (Overwhelming Noise-to-Signal Ratio) • Nonparametric Estimation (M. L. E. does not make sense anymore here) Piecewise (Monthly) Constant Geometric Brownian Motion Ri = μ(Ri-1, Ri-2, …)+σ (Ri-1, Ri-2, …) ·εi 1 2 3 4 5 6 7 8 Curse of Dimensionality 9 10 11 12

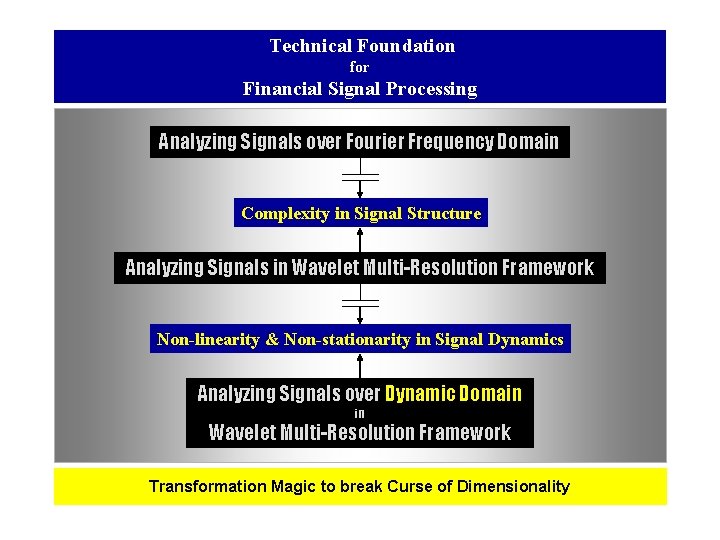
Technical Foundation for Financial Signal Processing Analyzing Signals over Fourier Frequency Domain Complexity in Signal Structure Analyzing Signals in Wavelet Multi-Resolution Framework Non-linearity & Non-stationarity in Signal Dynamics Analyzing Signals over Dynamic Domain in Wavelet Multi-Resolution Framework Transformation Magic to break Curse of Dimensionality

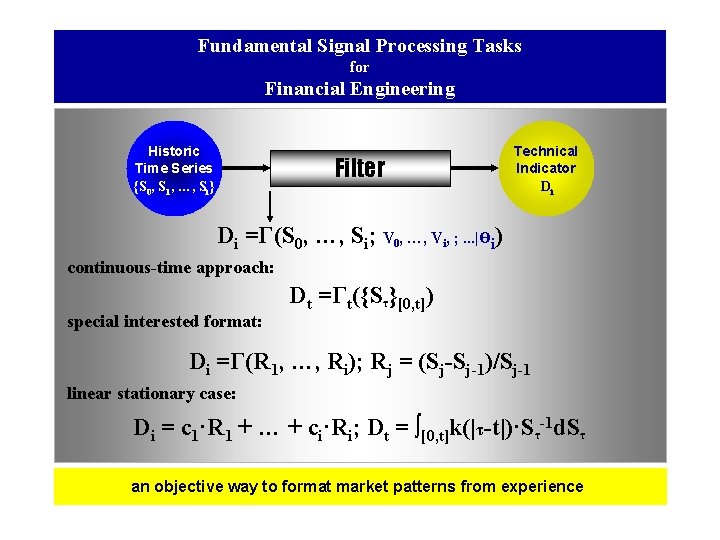
Fundamental Signal Processing Tasks for Financial Engineering Historic Time Series {S 0, S 1, …, Si} Filter Technical Indicator Di Di =Г(S 0, …, Si; V 0, …, Vi, ; . . . |өi) continuous-time approach: special interested format: Dt =Гt({Sτ}[0, t]) Di =Г(R 1, …, Ri); Rj = (Sj-Sj-1)/Sj-1 linear stationary case: Di = c 1·R 1 + … + ci·Ri; Dt = ∫[0, t]k(|τ-t|)·Sτ-1 d. Sτ an objective way to format market patterns from experience

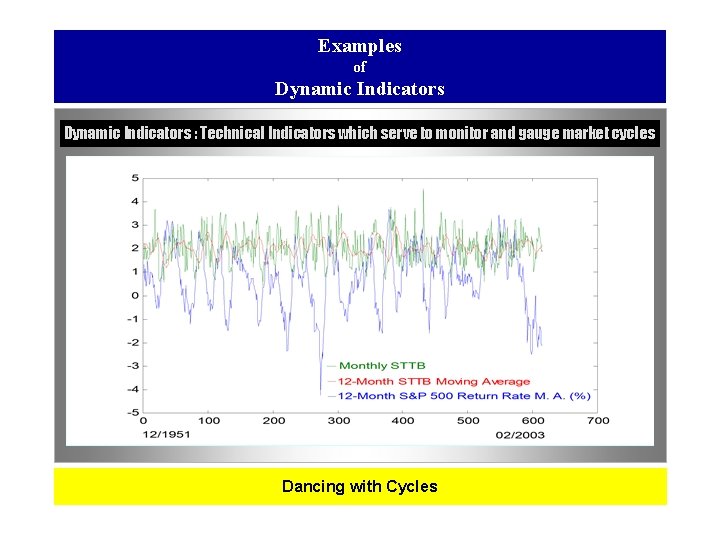
Examples of Dynamic Indicators : Technical Indicators which serve to monitor and gauge market cycles Dancing with Cycles

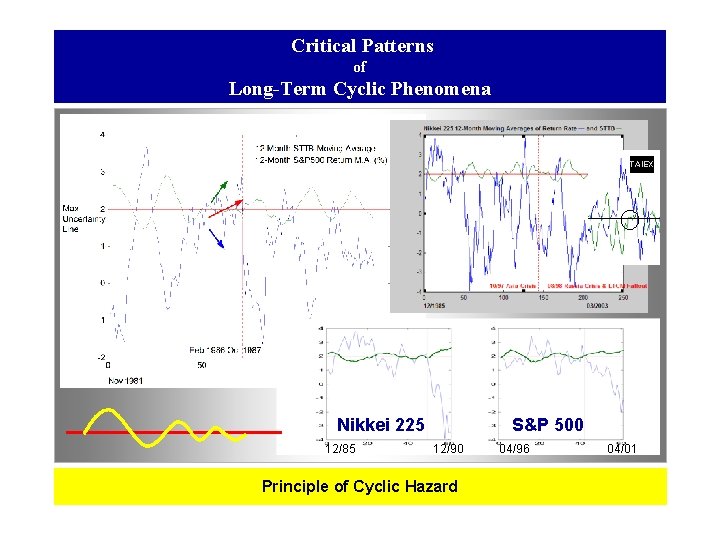
Critical Patterns of Long-Term Cyclic Phenomena TAIEX Nikkei 225 12/85 S&P 500 12/90 Principle of Cyclic Hazard 04/96 04/01

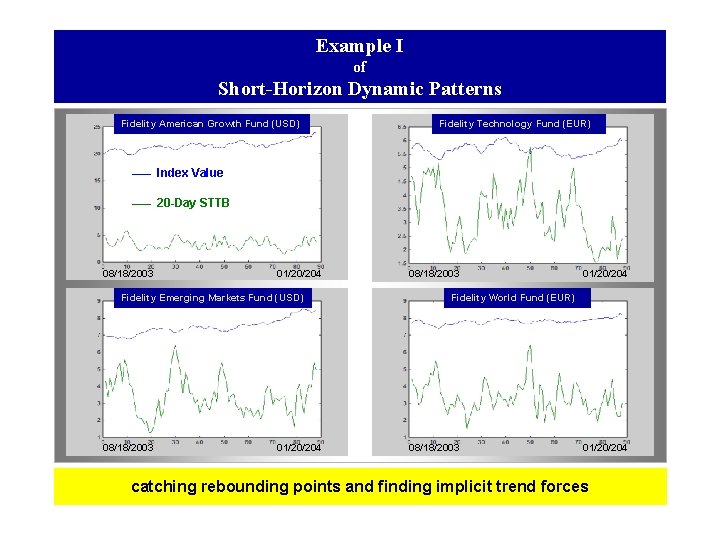
Example I of Short-Horizon Dynamic Patterns Fidelity American Growth Fund (USD) Fidelity Technology Fund (EUR) Index Value 20 -Day STTB 08/18/2003 01/20/204 Fidelity Emerging Markets Fund (USD) 08/18/2003 01/20/204 Fidelity World Fund (EUR) 08/18/2003 01/20/204 catching rebounding points and finding implicit trend forces

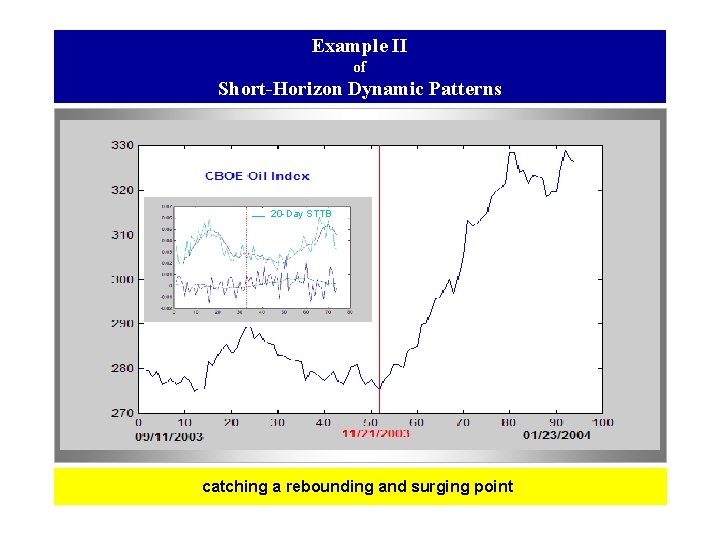
Example II of Short-Horizon Dynamic Patterns 20 -Day STTB catching a rebounding and surging point

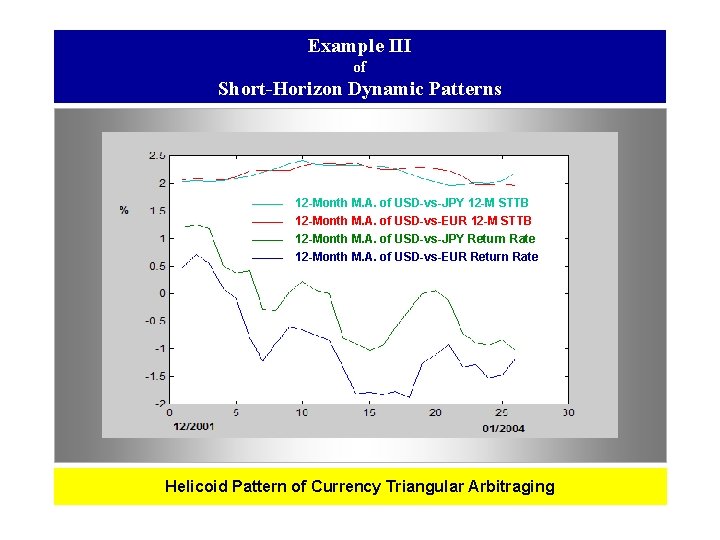
Example III of Short-Horizon Dynamic Patterns 12 -Month M. A. of USD-vs-JPY 12 -M STTB 12 -Month M. A. of USD-vs-EUR 12 -M STTB 12 -Month M. A. of USD-vs-JPY Return Rate 12 -Month M. A. of USD-vs-EUR Return Rate Helicoid Pattern of Currency Triangular Arbitraging

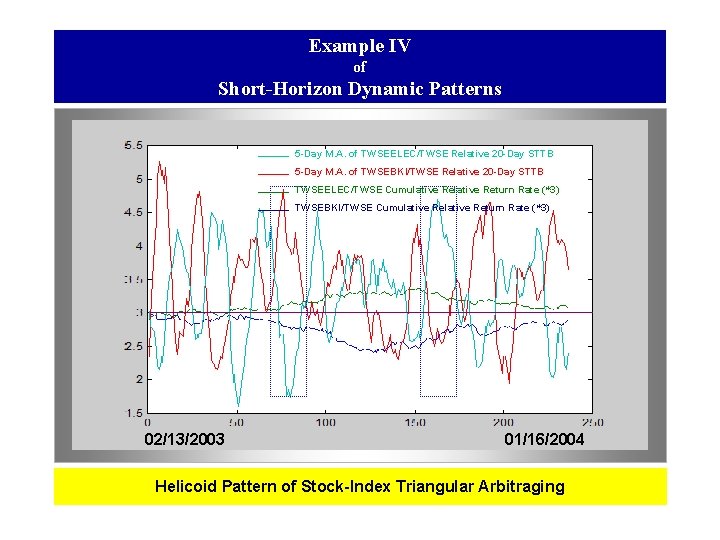
Example IV of Short-Horizon Dynamic Patterns 5 -Day M. A. of TWSEELEC/TWSE Relative 20 -Day STTB 5 -Day M. A. of TWSEBKI/TWSE Relative 20 -Day STTB TWSEELEC/TWSE Cumulative Return Rate (*3) TWSEBKI/TWSE Cumulative Return Rate (*3) 02/13/2003 01/16/2004 Helicoid Pattern of Stock-Index Triangular Arbitraging

Conditions of Modeling Potential • Physical Meanings - indicating practical market sense, e. g. momentum, uncertainty, stability, liquidity, … etc. • Cycle-Leading - e. g. • Consistency & Universality (Time & Geography) warning : markets might have no real intentions, but filters’ illusions!

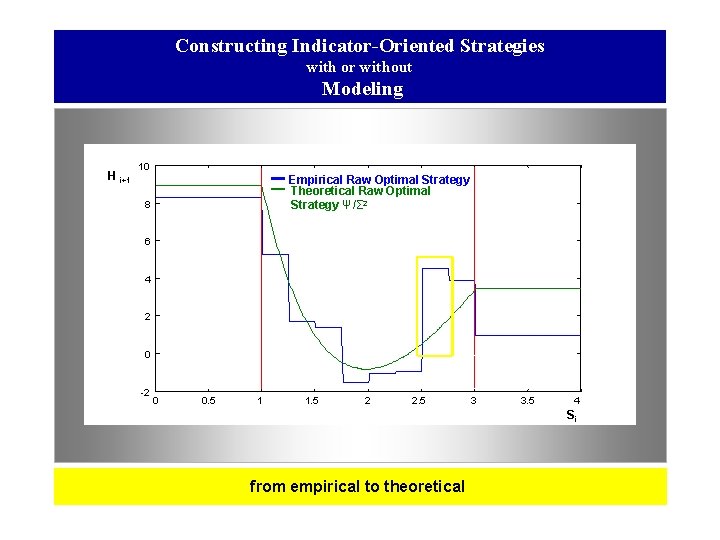
Constructing Indicator-Oriented Strategies with or without Modeling H i+1 10 Empirical Raw Optimal Strategy Theoretical Raw Optimal Strategy Ψ/Σ 2 8 6 4 2 0 -2 0 0. 5 1 1. 5 2 2. 5 3 3. 5 4 Si from empirical to theoretical

Methodological Framework of Modeling Capital Markets Rational Memory Process Market Aggregation Rationality Ri+1 -ri = Ψө(Di) + Ση(Di)·εi+1 Market Background Conditions continuous-time approach (with a linear stationary filter): d. St/St = Ψө(∫[0, t]k(|τ-t|)·Sτ-1 d. Sτ) ·dt + Ση(∫[0, t]k(|τ-t|)·Sτ-1 d. Sτ)·d. Wt dynamics based on rationality oriented by memory filtered by dynamic kernel

Advantages on Dynamic Domain • neatly constructing dynamic investment strategies on the dynamic domain • analytic calculation of risk-return trade-off curve via calculus of variation • easily formulating integrated-volatility for simulating risk-neutral probability density and calculating Va. R • turning nonlinear dynamic auto-regression into static nonparametric regression • introducing adaptive statistical estimation methods to separate stationary and non-stationary factors • assessing modeling risk • paving a way to “statistical finance” (market energy) • keeping the modeling framework flexible and adaptive under reflexivity • pricing profitable financial knowledges based on valuable dynamic kernels building robust & adaptive models for financial engineering in magic domains