Modeling Calcium Concentration and Biochemical Reactions Avrama Blackwell

Modeling Calcium Concentration and Biochemical Reactions Avrama Blackwell George Mason University

Objectives ● ● Explain importance of and relation between biochemical reactions and calcium dynamics Present equations describing biochemical reactions and calcium dynamics Describe mechanisms modulating calcium concentration Demonstrate dynamics using small simulations

Importance of Calcium ● ● Calcium influences channel behavior, and thereby spike dynamics – Short term influences on calcium dependent potassium channels – Long term influences such as potentiation and depression via kinases Electrical activity influences calcium concentration via ICa

Importance of Biochemical Reactions ● ● ● Some mechanisms of calcium dynamics are modeled as biochemical reactions Second messengers, . e. g Dopamine, modulate channel behavior Second messenger pathways are modeled as biochemical reactions

Biochemical Reactions ● Bimolecular Reactions – Stoichiometric interactions between substrate molecules to form product molecule ● ● ● Formation of bond between the substrate molecules Stoichiometric implies that the reaction specifies the number of each molecule required for reaction Molecules are consumed in order to make product

Biochemical Reactions ● Bimolecular Reactions – Reaction order is the number of simultaneously interacting molecules ● ● ● First order reaction: single substrate becomes product Rate constants: rate (units of per sec) at which substrate becomes product Ratio of rate constants gives concentration of substrates and products at equilibrium

When to Model Biochemical Reactions ● Metabotropic Receptors – Protein does not form channel – Protein is linked to GTP binding protein – Effect mediated by ● Activated G protein subunits ● Down stream second messengers

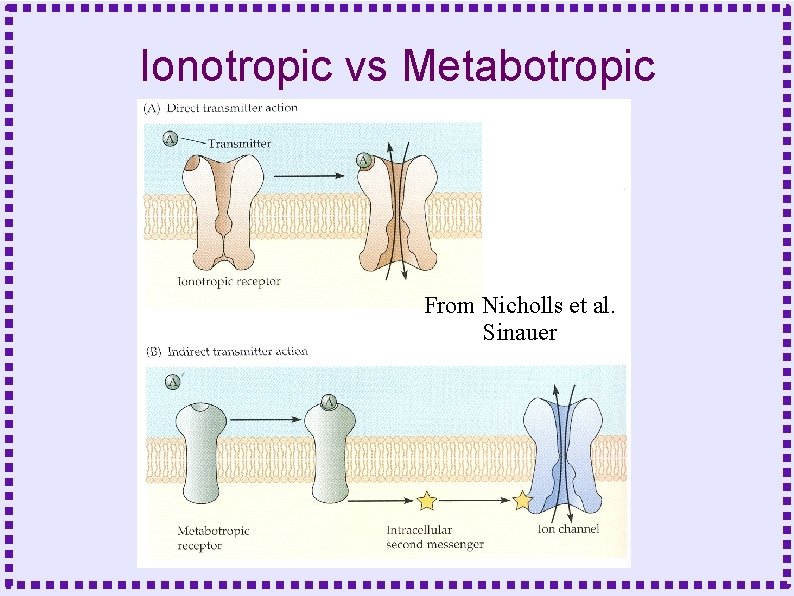
Ionotropic vs Metabotropic From Nicholls et al. Sinauer

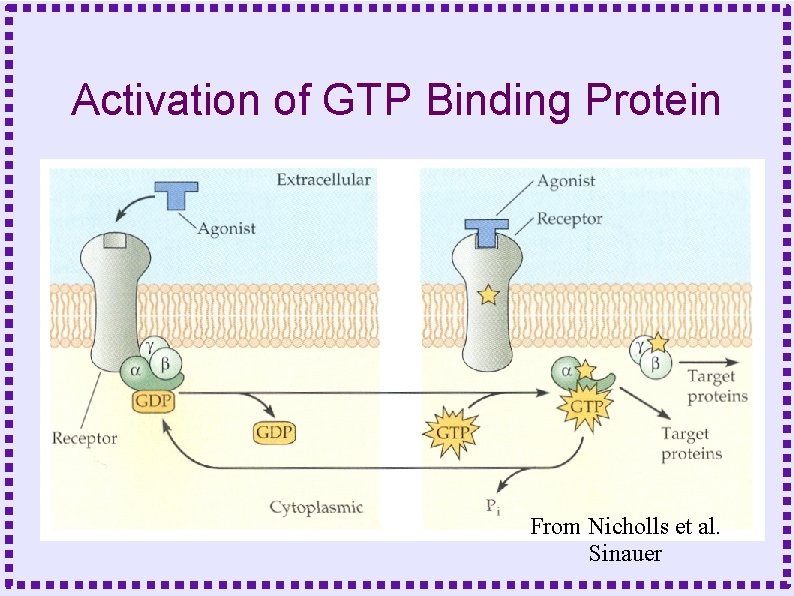
Activation of GTP Binding Protein From Nicholls et al. Sinauer

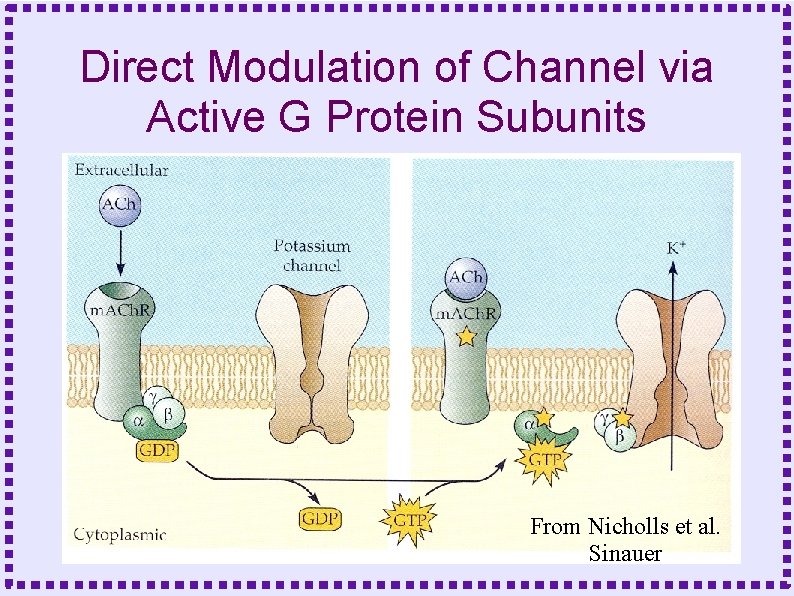
Direct Modulation of Channel via Active G Protein Subunits From Nicholls et al. Sinauer

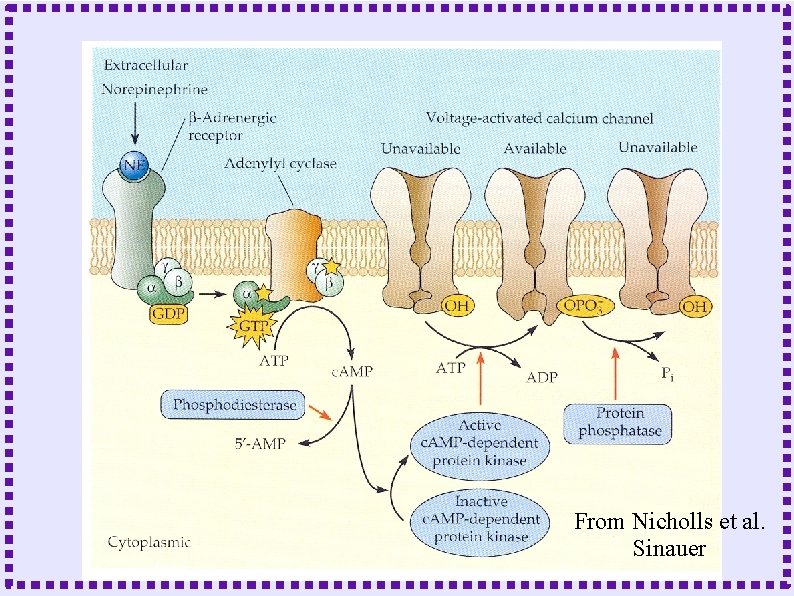
From Nicholls et al. Sinauer

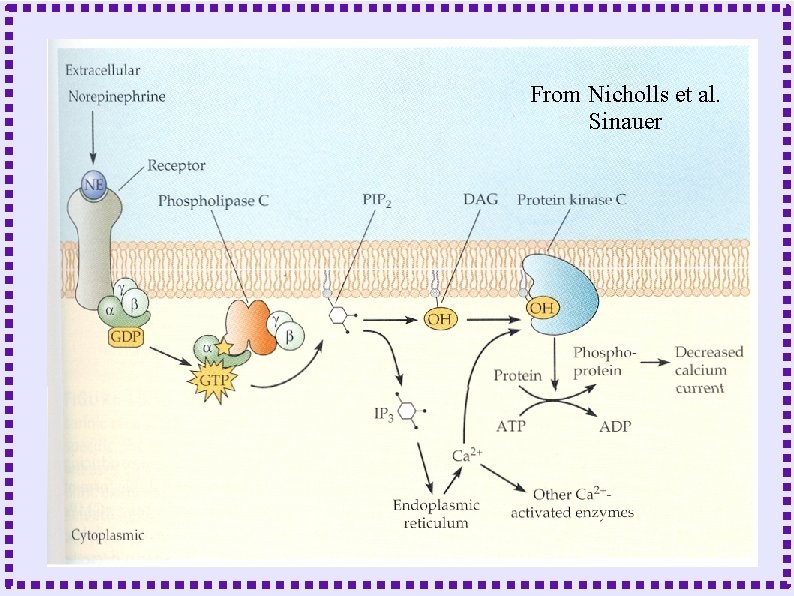
From Nicholls et al. Sinauer

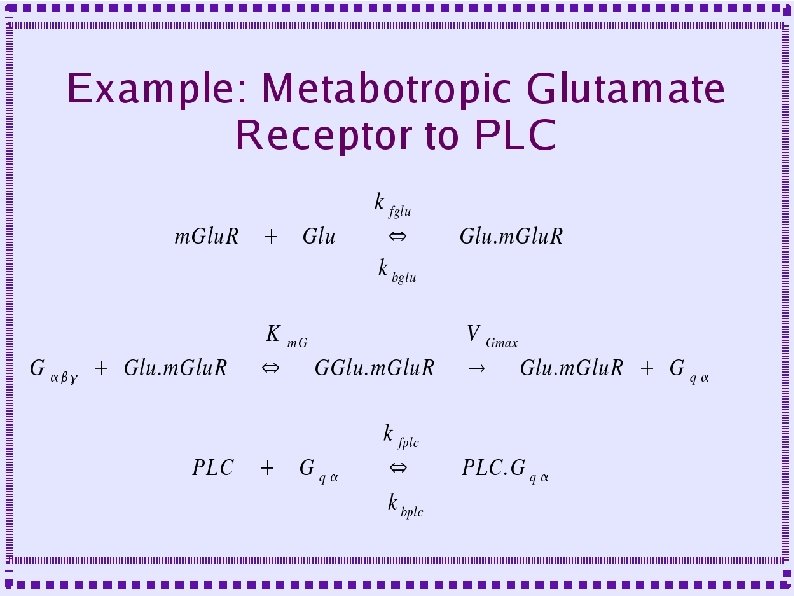
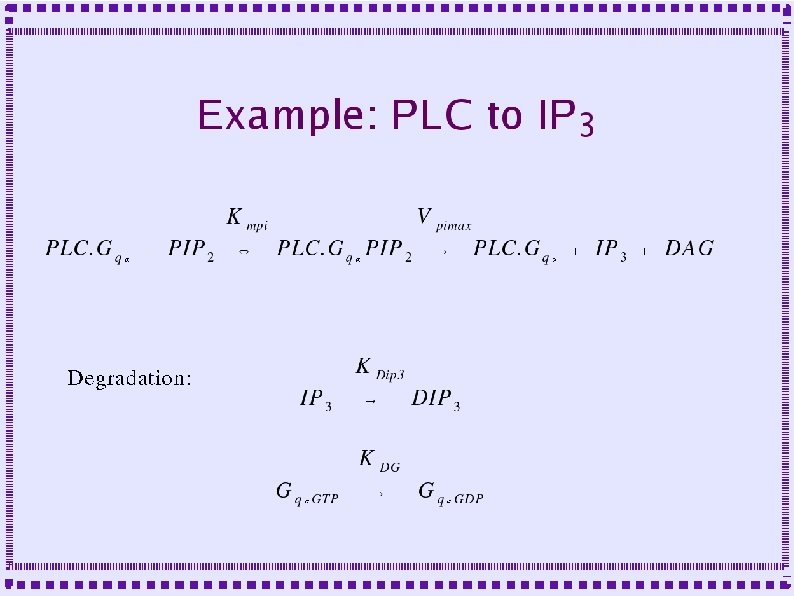
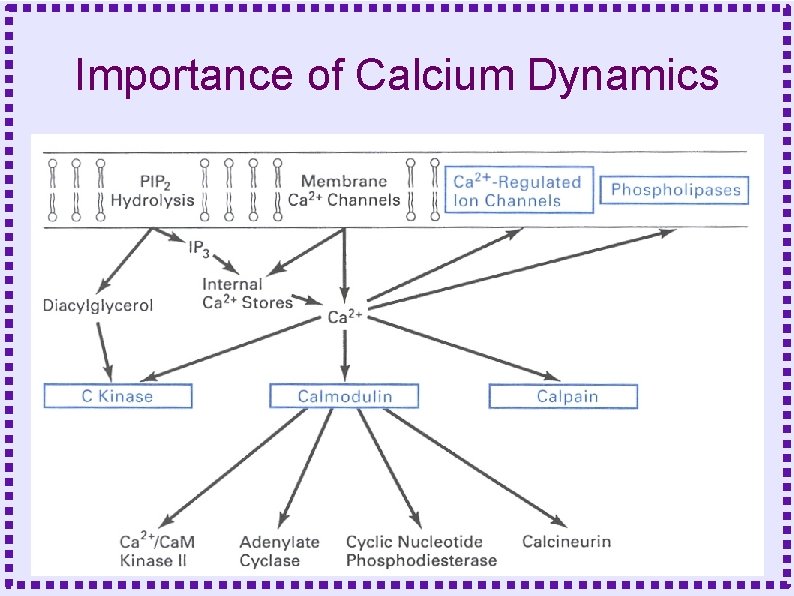
Importance of Calcium Dynamics

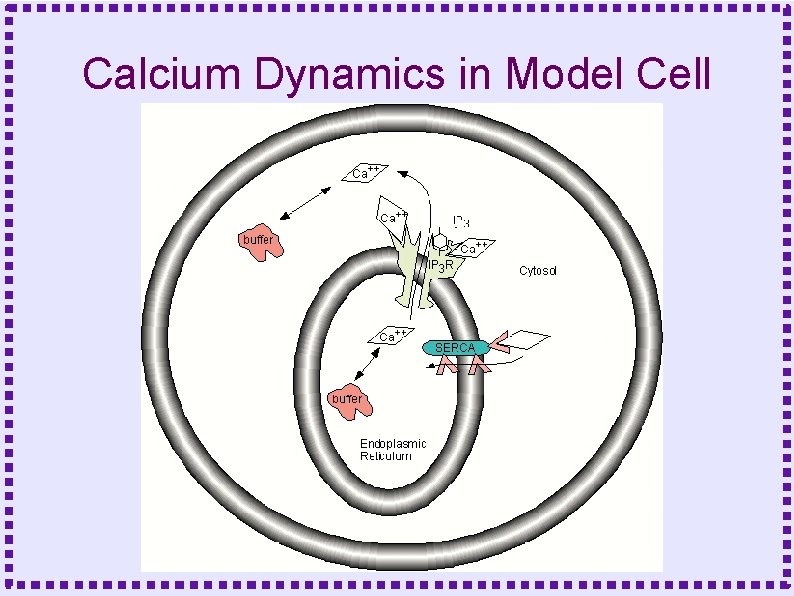
Control of Calcium Dynamics ● Calcium Current ● Pumps – Smooth Endoplasmic Calcium ATPase (SERCA) – Plasma Membrane Calcium ATPase (PMCA) – Sodium-Calcium exchanger

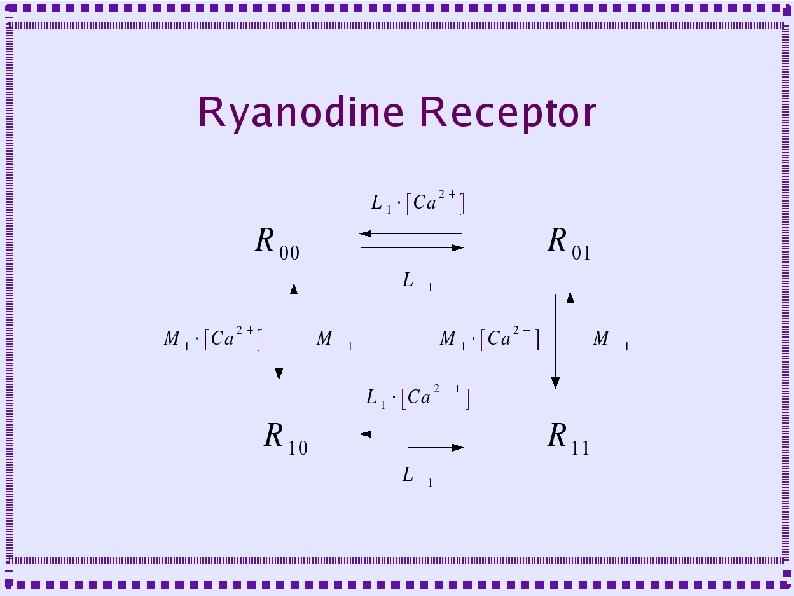
Control of Calcium Dynamics ● Release from Intracellular Stores – IP 3 Receptor Channel (IP 3 R) – Ryanodine Receptor Channel (Ry. R) ● Buffers ● Diffusion

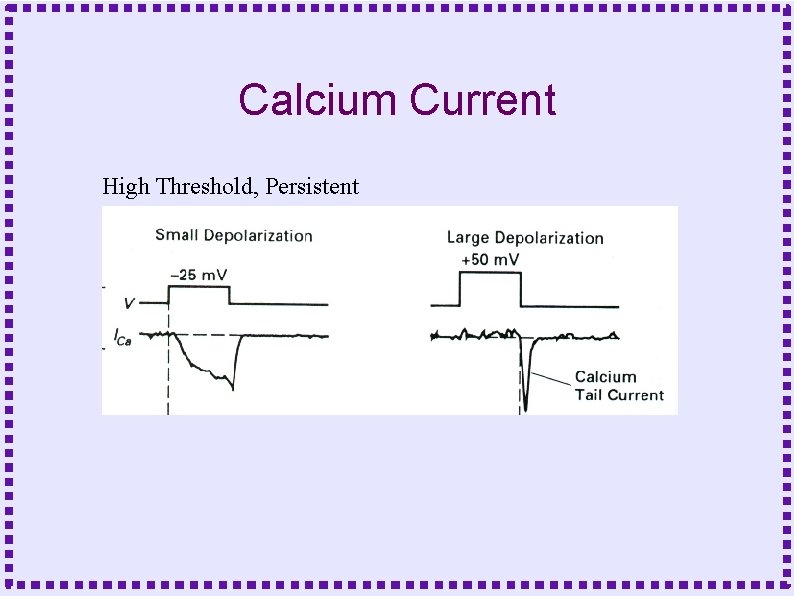
Calcium Current High Threshold, Persistent

Derivation of Diffusion Equation ● Diffusion in a cylinder – Derive equation by looking at fluxes in and out of a slice of width Dx

Derivation of Diffusion Equation ● Flux into left side of slice is q(x, t) ● Flux out of right side is q(x+Dx, t) – ● Fluxes may be negative if flow is in direction opposite to arrows Area for diffusional flux is A

Radial and Axial Diffusion From Koch and Segev, MIT Press Chapter 6 by De. Schutter and Smolen

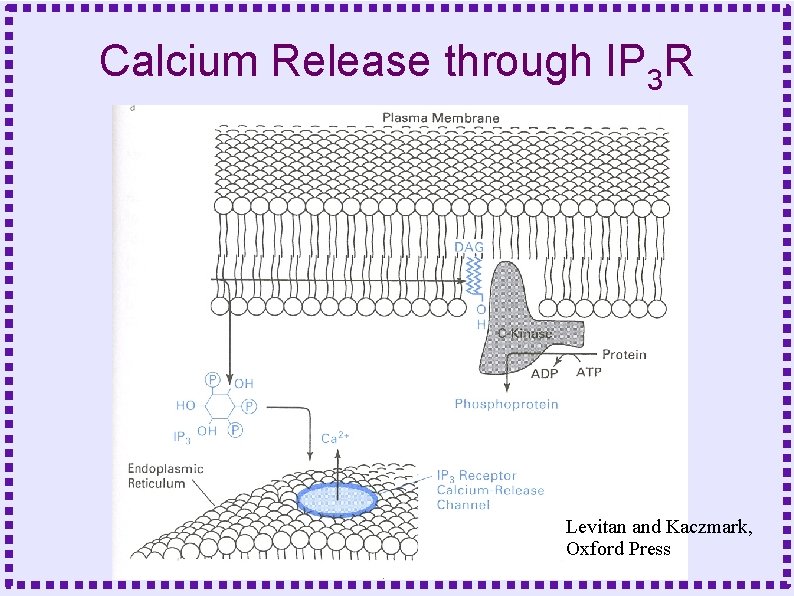
Calcium Release through IP 3 R Levitan and Kaczmark, Oxford Press

Calcium Release ● Receptors are modeled as multi-state molecules – One state is the conducting state – For IP 3 Receptor state transitions depend on calcium concentration and IP 3 concentration – For Ryanodine Receptor, state transitions depend on calcium concentration

Dynamics of Release Channels ● ● Both IP 3 R and Ry. R have two calcium binding sites: – Binding to one site is fast, causes fast channel opening – Binding to other site is slower, causes slow channel closing IP 3 R has an additional binding site for IP 3

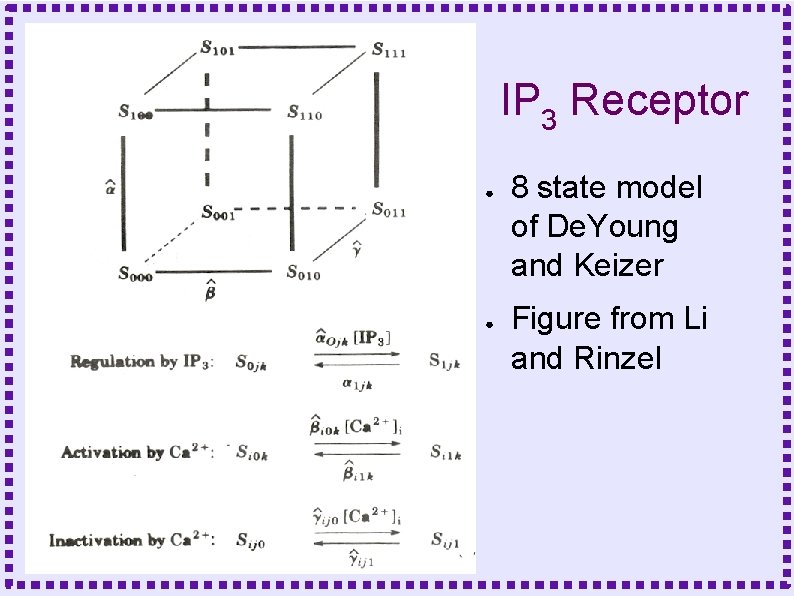
IP 3 Receptor ● ● 8 state model of De. Young and Keizer Figure from Li and Rinzel

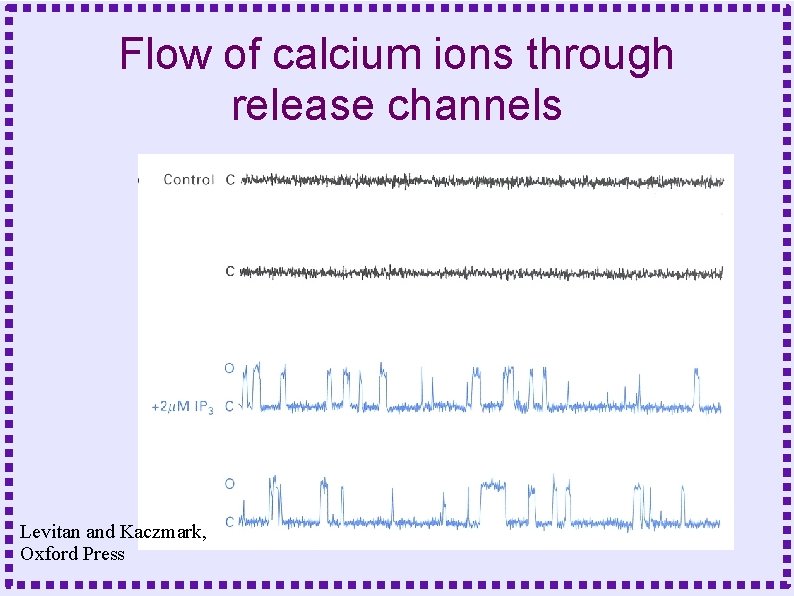
Flow of calcium ions through release channels Levitan and Kaczmark, Oxford Press

Dynamics of Release Channels ● Dynamics similar to sodium channel: – IP 3 + low calcium produces small channel opening – Channel opening increases calcium concentration – Higher concentration causes larger channel opening – Positive feed back produces calcium spike

Dynamics of Release Channels ● ● High calcium causes slower channel closing – Slow negative feedback – Channel inactivates – Inactivation analogous to sodium channel inactivation SERCA pumps calcium back into ER – Calcium concentration returns to basal level

Calcium ATPase Pumps ● ● Plasma membrane (PMCA) – Extrudes calcium to extracellular space – Binds one calcium ion for each ATP – Affinity ~300 -600 n. M Smooth Endoplasmic Reticulum (SERCA) – Sequesters calcium in SER – Binds two calcium ions for each ATP – Affinity ~100 n. M

Sodium Calcium Exchange (NCX) ● Stoichiometry – ● ● 3 (maybe 4) sodium exchanged for 1 calcium Charge transfer – Unequal => electrogenic – One proton flows in for each transport cycle – Small current produces small depolarization Theoretical capacity ~50 x greater than PMCA

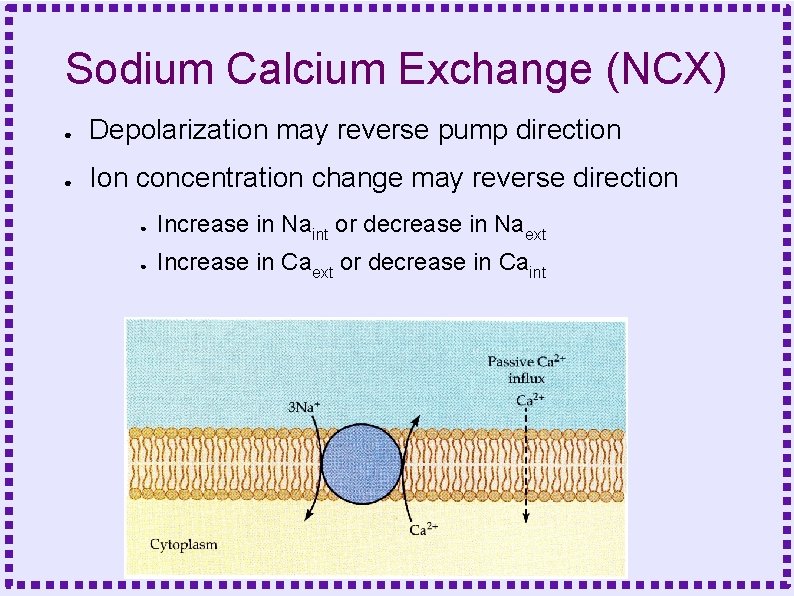
Sodium Calcium Exchange (NCX) ● Depolarization may reverse pump direction ● Ion concentration change may reverse direction ● Increase in Naint or decrease in Naext ● Increase in Caext or decrease in Caint

GENESIS objects ● Compartment-like objects – Keep track of molecule quantities and concentrations ● – Similar to compartment calculating voltage Requires geometry/morphology values ● length ● radius ● area of outer surface ● area of inner surface (can be zero) ● area of side surface ● volume

GENESIS objects ● Keep track of molecule quantities and concentrations – rxnpool (Chemesis) ● ● d. C/dt = A - B C A = change in quantity independent of present quantity B = rate of change Receives messages with quantities A and B from other objects (enzymes, reactions, also calcium influx)

GENESIS objects ● Keep track of molecule quantities and concentrations – conservepool (Chemesis) ● ● – C = Ctot - Ci Quantity is remainder after all other forms of molecule accounted for. pool (Kinetikit) ● d. C/dt = A - B C ● Or C = Ctot - Ci (if flag is set to conserve) ● Can also implement stochastic reactions

GENESIS objects ● Calculate changes due to reactions – mmenz (Chemesis) ● Use if MM assumptions are met ● Fields: Km and Vmax ● Inputs: Enzyme, substrate concentration ● Calculates Vmax times [Enzyme] times substrate ● Empirical feedback modification of enzyme activity can be added.

GENESIS objects ● Calculate changes due to reactions – – Enzyme (Chemesis) ● Fields: Kcat, Kf, Kb ● Inputs: enzyme, substrate quantity ● Calculates amount of Enzyme-Substrate complex ● Calculates change in product, enzyme, substrate Enz (kinetikit) ● Fields: Kcat, Kf, Kb ● Inputs: enzyme, substrate quantity ● Can implement stochastic reactions

GENESIS objects ● Calculate changes due to reactions – reaction (Chemesis) or reac (kinetikit) ● Fields: kf, kb ● Inputs: substrates and products ● Calculates: – – forward rate constant times substrate molecules backward rate constant times product molecules

Chemesis Objects ● ● CICR implements calcium release states – One element for each state – One of the elements may be conserved Parameters (Fields) – 'Forward' rate constants, – State vector, e. g. 001 for 1 Ca++ and 0 IP 3 bound – Fraction of receptors in this state – Whether this element is conserved

Chemesis Objects ● CICR (cont. ) ● Messages (Inputs) required: ● – IP 3 concentration – Cytosolic Ca++ concentration – fraction of molecules in states that can transition to this state – rate constant governing transition from other states to this state Calculates – Fraction of molecules in the state

Chemesis Objects ● CICRFLUX implements calcium release ● Messages (inputs) required: ● ● – Calcium concentration of ER – Calcium concentration of Cytosol – Fraction of channels in open state, X Parameters (Fields) – Permeability, P – Number of independent subunits, q q Calculates Ca flux = P*X (Ca. ER-Ca. Cyt)

Chemesis Objects ● Diffusion ● Parameters (Fields) – ● Messages (Inputs) – ● Diffusion constant, D Length, concentration, surface area from two reaction pools Calculates – Flux from one pool to another – D SA Conc / len

Chemesis Objects ● Implemented using CICRFLUX ● Messages (inputs) required: ● – Calcium of cytosol – Calcium of ER or EC space – Value of 1. 0 instead of open state Parameters (Fields) – Maximal Permeability (PL) – Hill coefficient (should be 1. 0)

Chemesis objects ● MMPUMP used for SERCA or PMCA Pump ● Fields ● – Affinity – Power (exponent) – Maximum rate Messages (inputs) – ● Concentration Calculates flux due to pump

Integrating Calcium Mechanisms ● RXNPOOL takes flux messages from various calcium sources – VDCC sends message CURRENT, with fields current and charge – Diffusion and release send message RXN 2 MOLES or RXN 2, with fields difflux 1 and difflux 2, or fluxconc 1 and fluxconc 2, respectively – Mmpump sends message RXN 0 MOLES with field moles-out (to cytosol) or moles_in – Reactions send messages RXN 0 - RXN 2

Genesis Calcium Objects ● Ca_concen – Simplest implementation of calcium – Fields ● Time constant of decay ● Minimum calcium ● – B = 1 / (z F vol): volume to produce 'reasonable' calcium concentration Inputs ● Calcium current

Genesis Calcium Objects ● Code of all the following is in src/concen ● Concpool – Calcium concentration without diffusion – Fields: Shape and size – Inputs: ● Buffer rate constants, bound and free ● MMPump coefficients ● Influx and outflux of stores

Genesis Calcium Objects ● difshell – ● fixbuffer – ● concentration shell. Has ionic current flow, onedimensional diffusion, first order buffering and pumps, store influx Non-diffusible buffer (use with difshell) Difbuffer – Diffusible buffer (use with difshell)

Morphology of Model Cell

Calcium Dynamics in Model Cell