Modeling Blood Flow in Artery Yeh WeiTing October

Modeling Blood Flow in Artery Yeh, Wei-Ting October 14, 2014

Outline • Review • Tube law • Non-Newtonian flow – Cannon’s rheological model • Example: LBM in simulating blood flow in deformable vessel • Summary • Reference

Review • Space and time dependence of fluid dynamics is essential for studying pulsatile flow • The importance of vessel elasticity – Windkessel effect • The importance of vessel thickness • We face two questions in modeling blood flow in artery: • How to model blood flow (in LBM) • How to model the fluid-structure interaction (in LBM) http: //en. wikipedia. org/wiki/Windkessel_effect

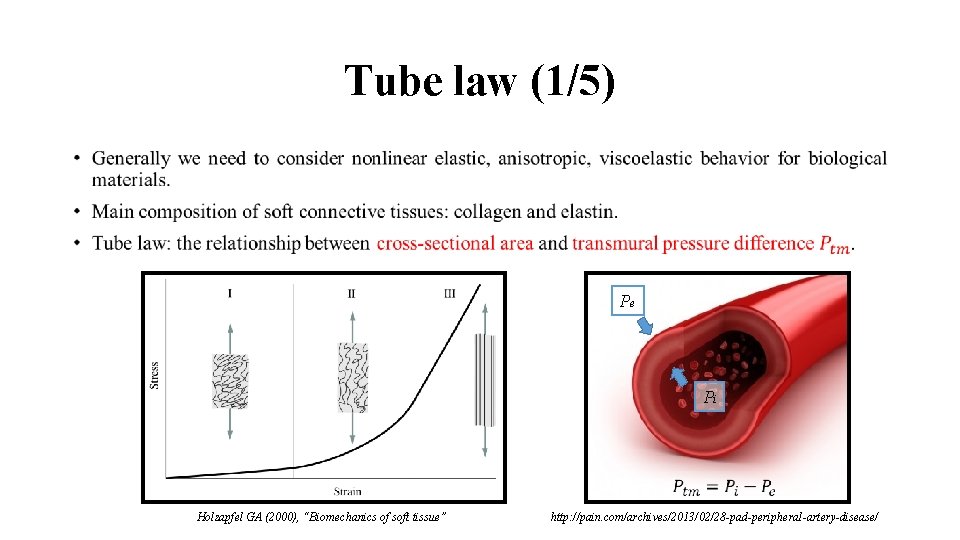
Tube law (1/5) • Pe Pi Holzapfel GA (2000), “Biomechanics of soft tissue” http: //pain. com/archives/2013/02/28 -pad-peripheral-artery-disease/

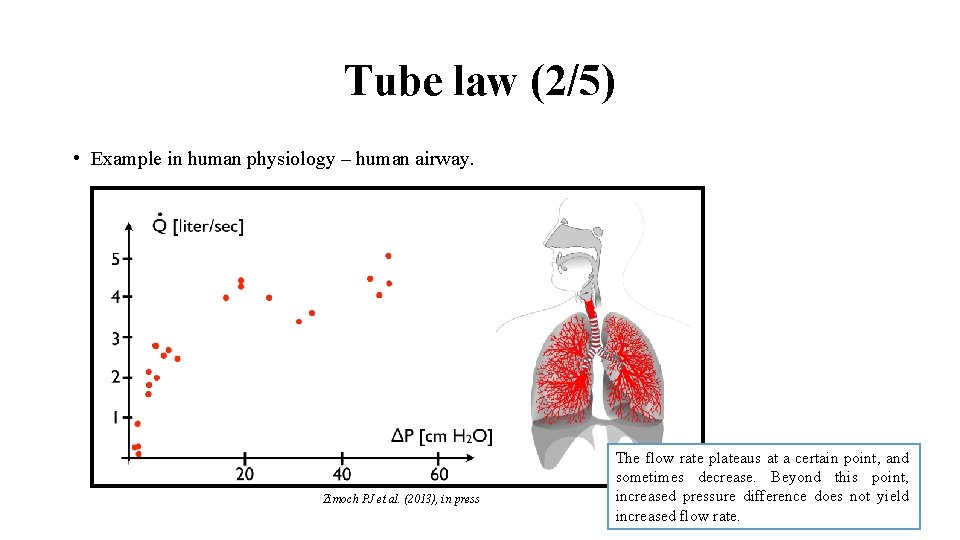
Tube law (2/5) • Example in human physiology – human airway. Zimoch PJ et al. (2013), in press The flow rate plateaus at a certain point, and sometimes decrease. Beyond this point, increased pressure difference does not yield increased flow rate.

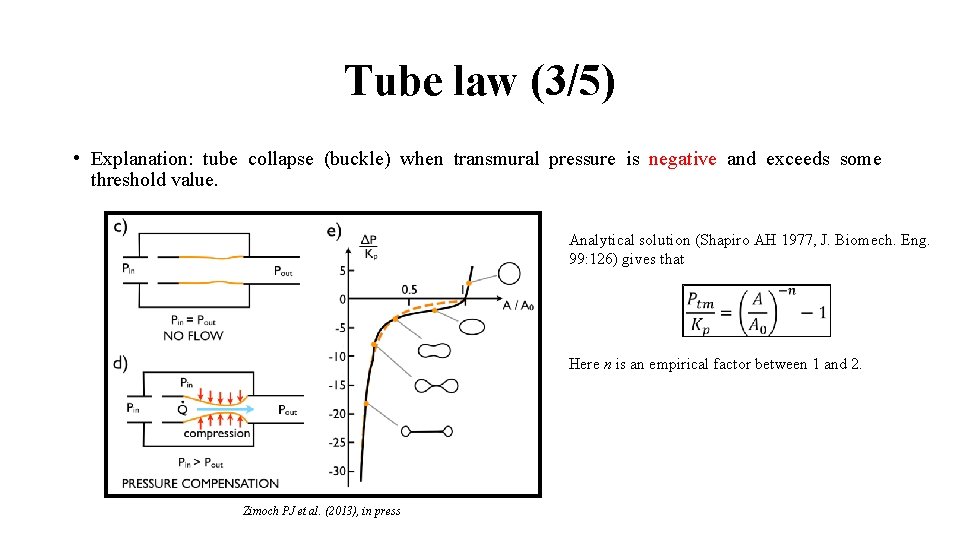
Tube law (3/5) • Explanation: tube collapse (buckle) when transmural pressure is negative and exceeds some threshold value. Analytical solution (Shapiro AH 1977, J. Biomech. Eng. 99: 126) gives that Here n is an empirical factor between 1 and 2. Zimoch PJ et al. (2013), in press

Tube law (4/5) • “General tube law for collapsible thin and thick-wall tubes” (Kozlovsky P et al. , 2014, J. Biomech. 47: 2378 -84). • In this study, the neo-Hookean hyperelastic model is used. They explored the role of wall thickness in post-buckling behavior of collapsible (one layered) tube. thickness Inner radius 1. Both thick and thin tube buckled at the same dimensionless transmural pressure. 2. The buckling cross sectional area is significantly lower for tubes with thick walls. 3. Once buckling occurred, thick-wall tubes were more compliant than thin-wall tubes.

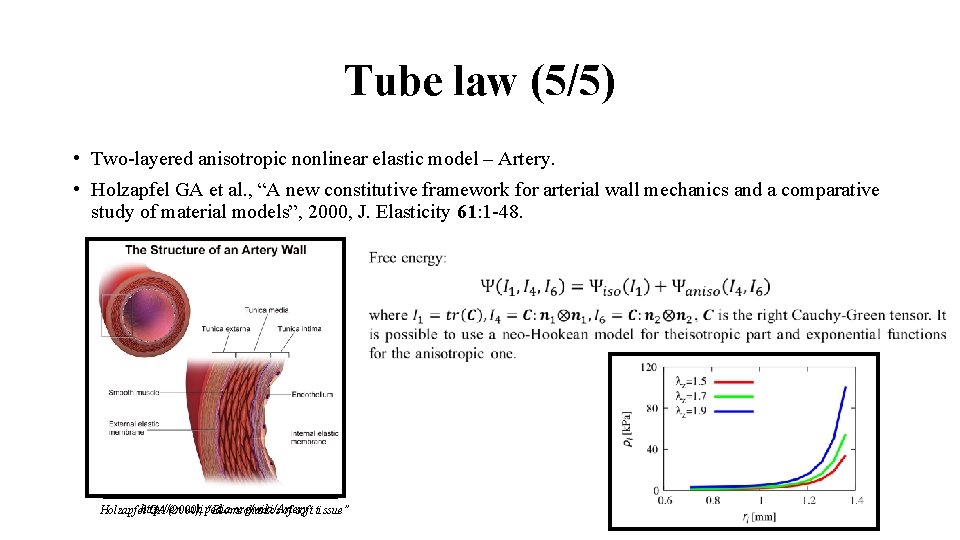
Tube law (5/5) • Two-layered anisotropic nonlinear elastic model – Artery. • Holzapfel GA et al. , “A new constitutive framework for arterial wall mechanics and a comparative study of material models”, 2000, J. Elasticity 61: 1 -48. Holzapfelhttp: //en. wikipedia. org/wiki/Artery GA (2000), “Biomechanics of soft tissue”

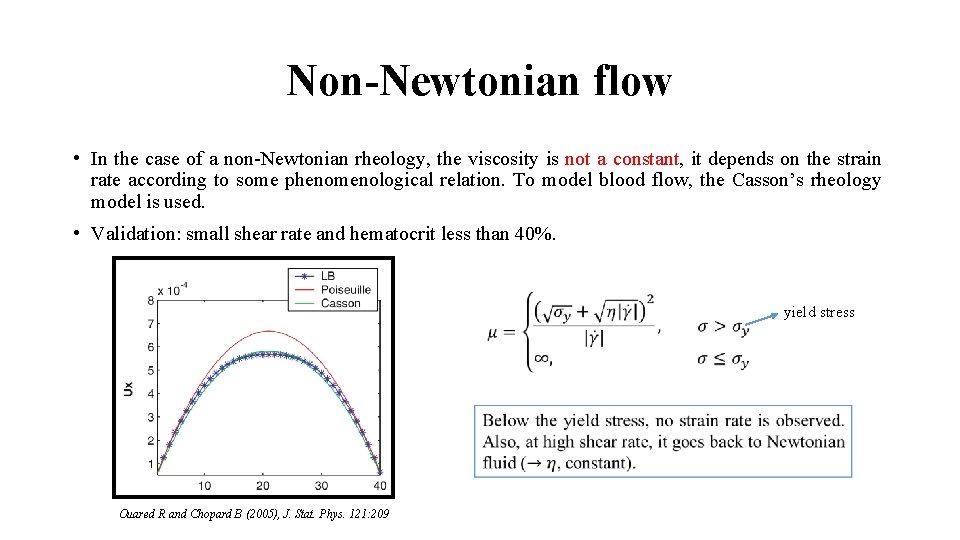
Non-Newtonian flow • In the case of a non-Newtonian rheology, the viscosity is not a constant, it depends on the strain rate according to some phenomenological relation. To model blood flow, the Casson’s rheology model is used. • Validation: small shear rate and hematocrit less than 40%. yield stress Ouared R and Chopard B (2005), J. Stat. Phys. 121: 209

Example of LB Model (1/3) • De Rosis A, “Analysis of blood flow in deformable vessels via a lattice Boltzmann approach”, 2014, Int. J. Modern Phys. C 25(4): 1350107. • Coupling the local relaxation time to local strain rate. Fluid-structure interaction is modeled by the tube law obtained from two layered artery model. • LB Boundary conditions: 1. Interpolated moving bouncing-back is used for tube-fluid boundary 2. Imposed density value on inflow and outflow section. Algorithm:

Example of LB Model (2/3)

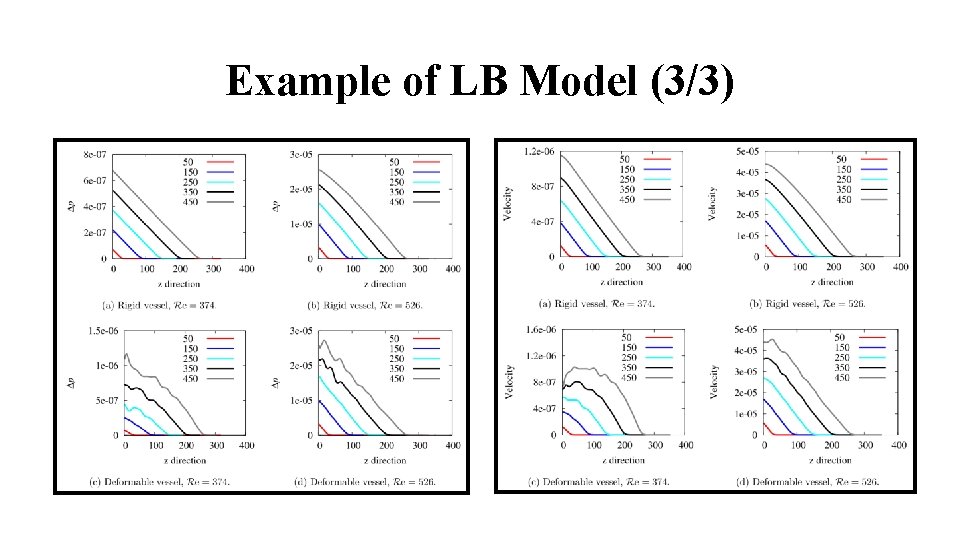
Example of LB Model (3/3)

Summary • General tube law and model of artery is reviewed. • LB can simulate non-Newtonian fluid. • In my simulation, we also must take the DP-tube interaction into consideration! How does it incorporate with tube law properly is another issue we need to solve.