Modeling and Simulations Atomistic Approach ByeongJoo Lee Dept

Modeling and Simulations - Atomistic Approach Byeong-Joo Lee Dept. of MSE Pohang University of Science and Technology (POSTECH) calphad@postech. ac. kr Byeong-Joo Lee www. postech. ac. kr/~calphad

Introduction – Modeling 대상 및 Atomistic Simulation 활용 분야 • 모델링/시뮬레이션의 대상 · (금속, 세라믹, 반도체) 소재 내부 원자 구조 발현 • 활용 분야 · Atomic Structures at surfaces, grain boundaries, interfaces · Defect (point defects and clusters, dislocations, surfaces) Chemistry · Defects 간, 또는 defect와 interfaces 간의 상호작용 · Phase Transformations · Cracks and Mechanical behavior Byeong-Joo Lee www. postech. ac. kr/~calphad

참고문헌 • “A Molecular Dynamics Primer" Furio Ercolessi, ‘http: //www. sissa. it/furio/’, 1997. • "Molecular Dynamics Simulation – Elementary Methods" J. M. Haile, John Wiley & Sons, Inc. , 1992. • Lecture Note of Prof. V. Vitek at KAIST (2002) and SNU (2003). • 기타 관련 논문들 강의시간에 공지 예정 Byeong-Joo Lee www. postech. ac. kr/~calphad

Atomistic Simulation I. General Aspects of Atomistic Modeling II. Fundamentals of Molecular Dynamics III. Fundamentals of Monte Carlo Simulation IV. Semi-Empirical Atomic Potentials (EAM, MEAM) V. Analysis, Computation of Physical Quantities VI. Exercise using Simulation Code Byeong-Joo Lee www. postech. ac. kr/~calphad

General Aspects of Atomistic Simulation 1. Objectives · Equilibrium configuration of a system of interacting particles, Analysis of the structure and its relation to physical properties. · Dynamic development 2. Applications · Crystal Structure, Point Defects, Surfaces, Interfaces, Grain Boundaries, Dislocations, Liquid and glasses, … 3. Challenges · Time and Size Limitations · Interatomic Potential Byeong-Joo Lee www. postech. ac. kr/~calphad

General Aspects of Atomistic Simulation • Equation of Motion • Potential Energy (e. g. pairwise interaction) • Potential Truncation · Radial Cutoff · Long-range Correction · Neighbor List • Periodic Boundary Condition · Minimum image criterion · Free surfaces Byeong-Joo Lee www. postech. ac. kr/~calphad

General Aspects of Atomistic Simulation • Kinetic Energy • Temperature • Pressure Virial equation • Stress Tensor Byeong-Joo Lee www. postech. ac. kr/~calphad

General Aspects of Atomistic Simulation – Stress Tensor Equilibrium system @ 0 K Equilibrium system @ a finite temperature Thermally induced stress Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – Time Integration of equations of motion The Verlet algorithm Velocity Verlet algorithm Integration Algorithm Computing time and memory Numerical error Stability Energy/momentum conservation Reversibility Gear’s Predictor-corrector algorithm Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – Running, measuring and analyzing 1. Build-up : initial configuration and velocities 2. Speed-up : Radial cut-off and Neighbor list 3. Controlling the system · MD at constant Temperature · MD at constant Pressure · MD at constant Stress 4. Measuring and analyzing · Average values of physical quantities · Physical Interpretation from statistical mechanics Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – MD at constant temperature Scaling of velocities : To : Target value of temperature T : instantaneous temperature v(t+Δt/2) = sqrt (To/T) v(t) + ½ a(t)Δt Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – MD at constant pressure Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – MD at constant stress Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – MD at constant stress: Parrinello and Rahman Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – Analyzing: to confirm equilibrium Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – Analyzing : to confirm equilibrium Byeong-Joo Lee www. postech. ac. kr/~calphad

Molecular Dynamics – Analyzing: structure analysis Byeong-Joo Lee www. postech. ac. kr/~calphad

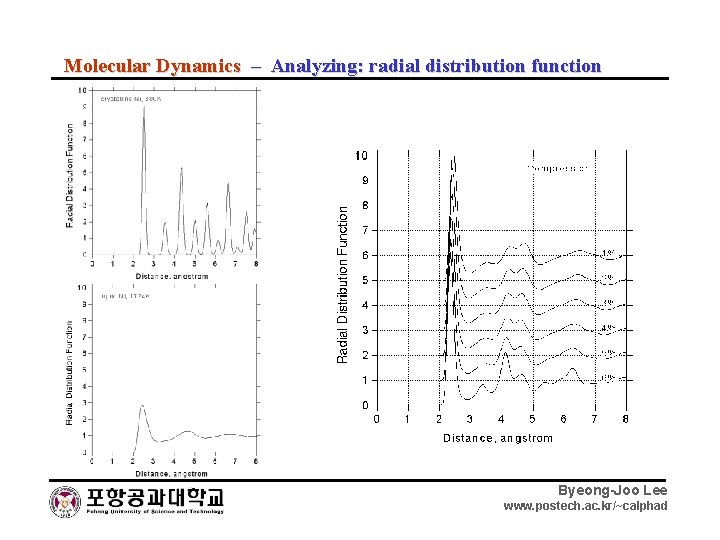
Molecular Dynamics – Analyzing: radial distribution function Byeong-Joo Lee www. postech. ac. kr/~calphad

(from Lecture Note of Prof. V. Vitek, 2002) Molecular Dynamics – Time average of a quantity Byeong-Joo Lee www. postech. ac. kr/~calphad

Physical Interpretation of MD using the concept of Statistical Mechanics Fluctuations Byeong-Joo Lee www. postech. ac. kr/~calphad

Physical Interpretation of MD using the concept of Statistical Mechanics Byeong-Joo Lee www. postech. ac. kr/~calphad

Physical Interpretation of MD - Autocorrelations Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Fundamentals (from Lecture Note of Prof. V. Vitek, 2002) Byeong-Joo Lee www. postech. ac. kr/~calphad

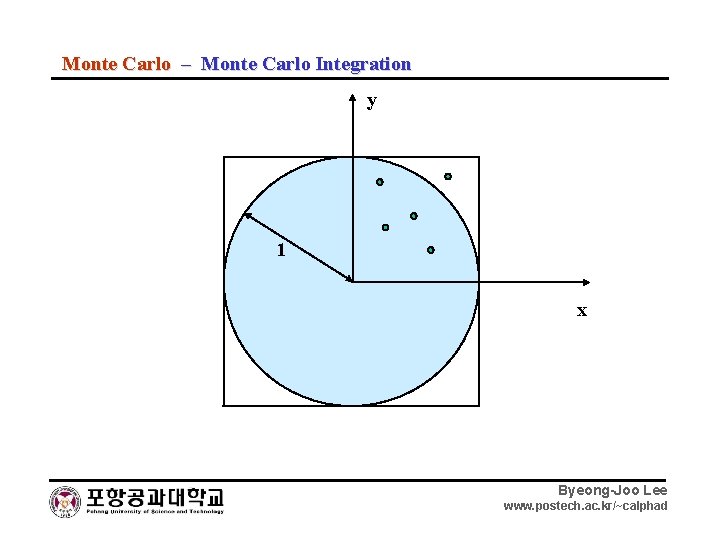
Monte Carlo – Monte Carlo Integration y 1 x Byeong-Joo Lee www. postech. ac. kr/~calphad

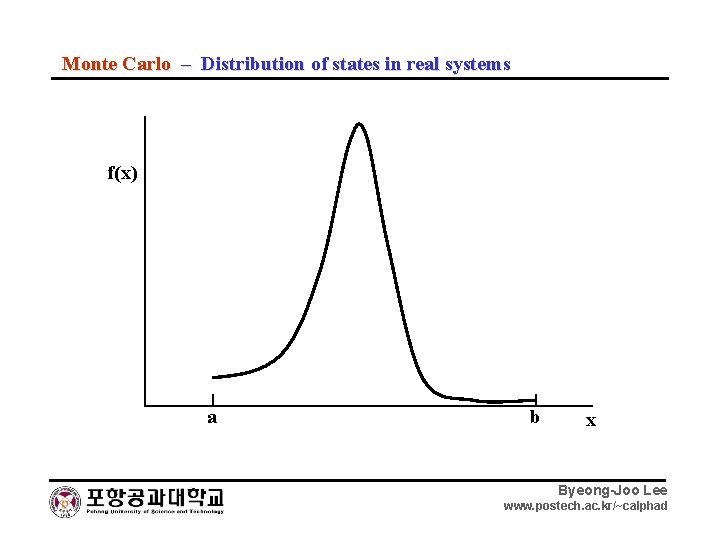
Monte Carlo – Distribution of states in real systems f(x) a b x Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – General Monte Carlo Algorithm Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Averages and fluctuations Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Errors in MC calculations Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Canonical Ensemble (N, V, T) Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Metropolis Method Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Examples of Metropolis Method Byeong-Joo Lee www. postech. ac. kr/~calphad

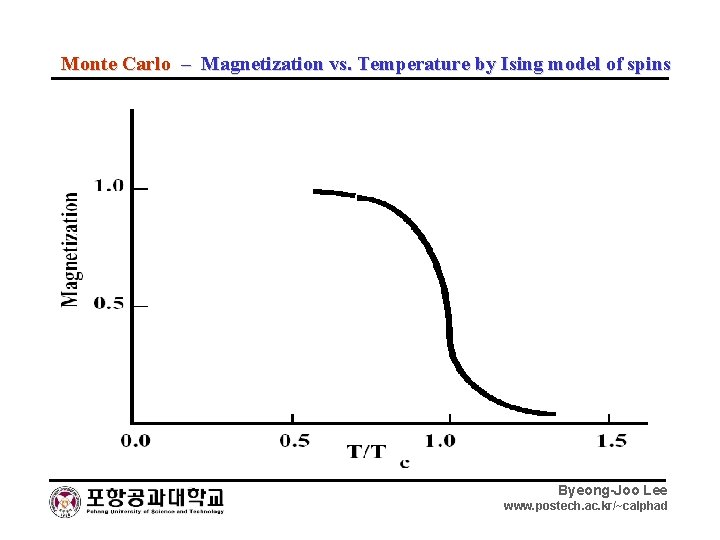
Monte Carlo – Magnetization vs. Temperature by Ising model of spins Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Isothermal-Isobaric Canonical Ensemble (N, P, T) Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Grand Canonical Ensemble (μ, V, T) The number of particles is variable - fluctuations of the concentration are allowed Generally, select randomly one of the procedures 1) Change of the configuration 2) Creation of a particle 3) Destruction of particles exp(-ΔEp/k. T) exp[-(ΔEp-μ)/k. T] exp[-(ΔEp+μ)/k. T] Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Modified Grand Canonical Ensemble (μ, V, T) Byeong-Joo Lee www. postech. ac. kr/~calphad

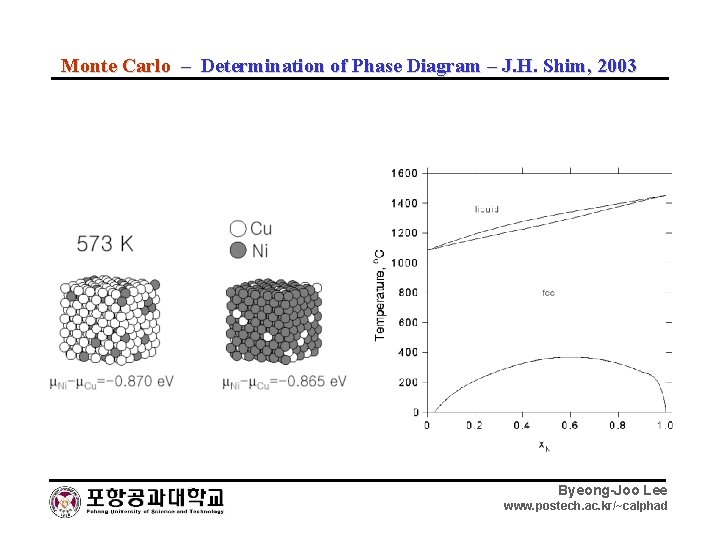
Monte Carlo – Determination of Phase Diagram – J. H. Shim, 2003 Byeong-Joo Lee www. postech. ac. kr/~calphad

Monte Carlo – Modified Grand Canonical Ensemble (μ, V, T) Segregation to an interface Order-disorder transition in binary alloy Byeong-Joo Lee www. postech. ac. kr/~calphad

Phase Separation and Surface Segregation in Cu-Ni Thin Films 298 K 373 K 473 K 800 K Byeong-Joo Lee www. postech. ac. kr/~calphad

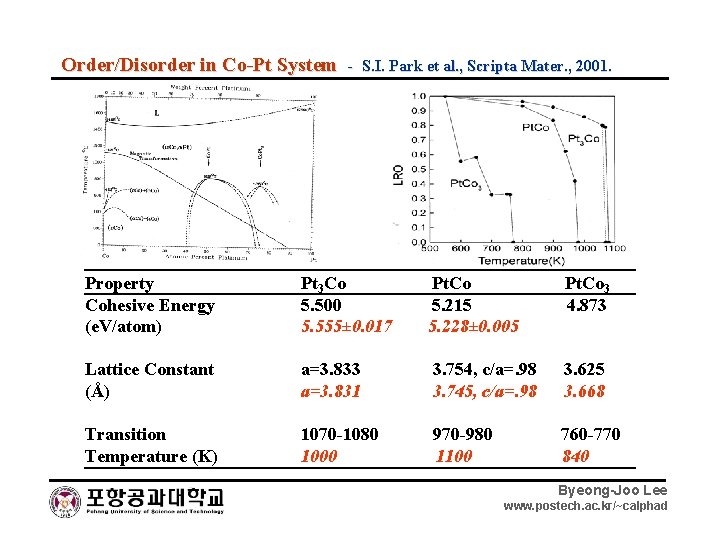
Order/Disorder in Co-Pt System - S. I. Park et al. , Scripta Mater. , 2001. Property Cohesive Energy (e. V/atom) Pt 3 Co 5. 500 5. 555± 0. 017 Pt. Co 5. 215 5. 228± 0. 005 Pt. Co 3 4. 873 Lattice Constant (Å) a=3. 833 a=3. 831 3. 754, c/a=. 98 3. 745, c/a=. 98 3. 625 3. 668 Transition Temperature (K) 1070 -1080 1000 970 -980 1100 760 -770 840 Byeong-Joo Lee www. postech. ac. kr/~calphad