MODELING AND SIMULATION OF COMPUTER NETWORKS AND SYSTEMS

MODELING AND SIMULATION OF COMPUTER NETWORKS AND SYSTEMS: METHODOLOGIES AND APPLICATIONS Performances Evaluation and Petri Nets Ousmane Diallo, Joel J. P. C. Rodrigues and Mbaye Sene

2 OUTLINE Introduction Modeling and Performance Evaluation Applications of Petri Nets Formalism of Petri Nets Stochastic Petri Nets (SPNs) Generalized Stochastic Petri Nets (GSPNs) Colored Petri Nets (CPNs) Well-formed Nets (WNs) Stochastic Well-formed Petri Nets (SWNs) Conclusion

3 Introduction Modeling and performance evaluation of discrete event systems, such as computer systems, communication networks and production systems have a lot of attention from different scientific communities. Scientific, economic and technical progress and the increasing complexity of these systems raise more new challenges and problems for their developers. In addition, imperfections in the design process can be negative factors in the development time, cost and operational efficiency in the system. Necessity of using effective methods or tools well suited that can help the designer in the design phase and in the exploitation phase. Invented in 1962 by Carl Adam Petri Net is a Mathematical and Graphical tool for modeling and performance evaluation of real systems with discrete events.

4 Introduction These systems are characterized as being concurrent, synchronous, asynchronous, distributed, parallel, nondeterministic and/or stochastic Graphical notations Provide a powerful communication medium between the different entities involved Mathematical notations Model can be defined by a set of linear algebraic equations, or other mathematical models that translate the behavior of the studied system Several enhancements were made to the basic model: Introduction of the concept of time, introduction of color, stochastic concept, introduction of inhibitor arcs, etc.

5 Modeling and Performance Evaluation: Modeling Possibility to model an already functioning or not yet existing system However, the study of a real system is rarely feasible in an operational environment Ø An analysis consisting to represent its functioning in a way more or less detailed is required After collecting the main characteristics of the system from the customer and knowing the required materials, the modeler can start modeling bearing in mind the objective to achieve Ø The use of tools (descriptive, mathematics, etc. ) is then necessary to reach this goal. Ø The real system to design is reproduced based on mathematical equations and diagrams that ignore certain details. Most often, the model takes into account certain parameters of the system and abandons others. The more the model is accurate, the more its analysis is difficult and sometimes not feasible. Then, there must be a compromise between an adequacy of the model and system and an easy analysis of the model.

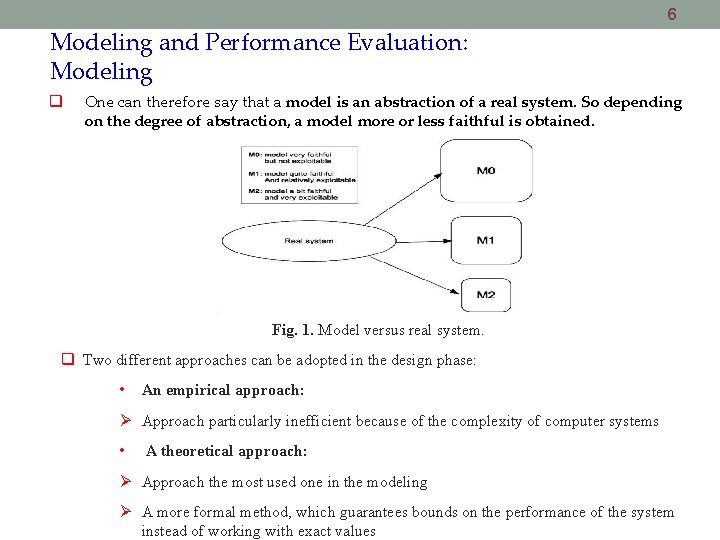
6 Modeling and Performance Evaluation: Modeling One can therefore say that a model is an abstraction of a real system. So depending on the degree of abstraction, a model more or less faithful is obtained. Fig. 1. Model versus real system. Two different approaches can be adopted in the design phase: • An empirical approach: Ø Approach particularly inefficient because of the complexity of computer systems • A theoretical approach: Ø Approach the most used one in the modeling Ø A more formal method, which guarantees bounds on the performance of the system instead of working with exact values

7 Modeling and Performance Evaluation: Performance evaluation Is interested in calculating the performance parameters or indices of a system The required indices are on different orders depending on the studied systems Five performance parameters that are important to determine in many systems are: • The throughput (often denoted X), • The waiting time (often denoted W), • The response time of a client, message or packet (often denoted R), • The number of clients, messages or packets (often denoted Q) • And the use rate (often denoted U) However, most of the time the mean values are in interest.

8 Modeling and Performance Evaluation: Why evaluate the performance of a system? The performance evaluation of a system is necessary when one wishes to know the performance of a system and that the direct measurements on the system cannot be performed. The performance evaluation can mainly intervene in two levels: • In Design: the system does not yet exist, it should be then created, sized. In practice, it is necessary to perform this phase with respect of a set of specifications. • In exploitation: the system does exist, however one wishes to modify or test it outside of its normal running. It will be question here to design a different system that meets new objectives. This phase is generally performed to make the system more efficient. The performance evaluation is also performed in research in order to justify the interest of a new solution, such as a new architecture, algorithm, protocol, etc.

9 Modeling and Performance Evaluation: How to evaluate the performance of a system? Directly measuring the performance parameters of the real system is very difficult, if not impossible. A mathematical formalism concentrating into a model, behavior and parameters that better reproduce the functioning of the system must be proposed Different types of formalism have been developed depending on the analysis required: • Networks of queues, • Stochastic Automata, • Petri nets, etc. Fig. 2. Illustration schema of the performance evaluation of a real system.

10 Modeling and Performance Evaluation: Analysis of the model There are two main types of analysis: • Qualitative analysis consists to check the structural and behavioral properties of the system, such as the absence of blocking (vivacity), the invariants of the system, stability, etc. • Quantitative analysis consists to calculate the performance parameters of the system There are two main approaches of quantitative analysis of performance: • The simulation called at discrete event consists to reproduce the evolution of the model, step by step, by studying a particular realization of the stochastic model. • The analytical methods (stochastic automata, etc. ) propose to calculate the performance indices mathematically by solving the underlying equations.

11 Modeling and Performance Evaluation: Analysis and documentation of the results The specification book contains the main objectives of the model The modeler introduces a margin of error in which the results should be, instead of a deterministic study The analysis of the results allows to verify if the results obtained are within the range previously defined Desirable to know the parameters which their change influences the results obtained Safeguarding the results of different executions with the parameters that lead to these results is very important in the validation of a model Can help the client in the future, for example, when he wants to increase the performance of the system, to know the parameters to modify therefore the material to change The documentation can also help to know the parameters that can be at the origin of an eventual loss of performance of the system during its running

12 Applications of Petri Nets Introduced in 1962 by Carl Adam Petri For evaluating the performances of real systems with discrete events, characterized as being concurrent, synchronous, asynchronous, distributed, parallel, nondeterministic and/or stochastic Used in many varieties of application areas, such as: • Industrial, • Computer sciences, • Biologic, • Study of organisms, etc. Two of the most successful application areas of Petri nets have been: • Modeling and performance evaluation • Communication protocols

13 Formalism of Petri Nets: Informal definition A Petri net is graphically represented by: Two kinds of nodes: • Places: represented by circles and usually model the state variables of the system (system resources) • Transitions: represented by a rectangle or a continuous line and represent an event and/or an action that changes the values of the state variables of the system Arcs are directed and always connect places and transitions showing then which resource is changed by what event Tokens represented by small discs. Each token represents a specific value of the variable modeled by the place that contains them

14 Formalism of Petri Nets: Formal definition A Petri net can be defined as a quadruplet: R=<P, T, Pre, Post> with: • • is a finite set of places, is a finite set of transitions, with P∪T≠∅ and P∩T=∅, • Pre: (P X T)�N is the application of precedent places, where N is a set of nonnegative integers, and • Post: (P X T)�N is the application of following places This notation below can also be used: C=Post-Pre with C generally known as the incidence matrix of the Petri net

15 Formalism of Petri Nets: Marked Petri net A state of the Petri net is represented by a marking A marked Petri net is the couple: R 0 = <R, M 0 > Where: • R is the Petri net and • M 0 is the initial marking of the network R; it is an application M 0: P�N M 0 (p) is the number of tokens contained in the place p

16 Formalism of Petri Nets: Petri net with inhibitor arc An inhibitor arc connecting a place p to a transition t prevents the latter to be fired if the place p contains a number of tokens higher or equal to the value of the arc, i. e. , M 0(p) ≥ arc_value A Petri net with inhibitor arc is defined by: Rinh = <R, Inh > where Inh is the application: Inh: P X T�N The inhibitor arc is represented by a line with a small circle at the extremity Fig. 3. Inhibitor arc

17 Formalism of Petri Nets: Example of Petri net Consider the Petri net of the graph Fig. 4. Example of a graph associated to a Petri net. In matrix notations, the Petri net of the Fig. 3 is defined as:

18 Formalism of Petri Nets: Example of modeling with Petri nets Consider two machines M 1 and M 2 communicating via two channels Ch 1 and Ch 2 in the following manner: Machine M 1 Machine M 2 While true do Begin While do Begin -Prepare the message (action t 1) -Send the message on Ch 1 (action t 2) -Read the acknowledgment sent by M 2 on Ch 2 (action t 3) -Interpret the acknowledgment (action t 4) -Read the message from M 1 on Ch 1 (action t 5) -Interpret the message (action t 6) -Prepare the acknowledgment (action t 7) -Send the acknowledgment to M 1 on Ch 2 (action t 8) End The Petri net of Fig. 5 can model the functioning of this above communication protocol. Fig. 4. Petri net for modeling a communication between sender and receiver.

19 Formalism of Petri Nets: Dynamic of a Petri net The evolution of a Petri net is obtained by the firing of transitions. Enabling of a transition A transition t is enabled in M if and only if: • ∀ p∈P, M(p) ≥ Pre(p, t) • And ∀ p∈P, M(p) < Inh(p, t) t is enabled can be expressed by the following notations: • M ≥ Pre(. , t) • M(t> • . Firing of a transition The firing of a transition t enabled in M leads to the marking M’ such that: • ∀ p∈P, M’(p) = M(p) – Pre(p, t) + Post(p, t) These notations below also can be used: • M’ = M – Pre(. , t) + Post(. , t) ; M(t>M’) or

20 Formalism of Petri Nets: Properties of a Petri net Markings graph • Considering a marked Petri net: R 0=<R, M 0 > • The reachability set, A (R; M 0), of a marked Petri net is the markings set that can be reached from the initial marking M 0 by a sequence of firings • When this markings set is finite, it can be represented as a graph called markings graph, GA (R; M 0) K-bounded place and binary • A place p of a marked Petri net R 0 is k-bounded if and only if: ∀ M'∈A(R; M 0) M'(p) ≤ k • If k=1, then the place is binary (safe) K-bounded marked Petri net and binary • A marked Petri net R 0 is k-bounded if and only if all its places are k-bounded. • A marked Petri net R 0 is binary (safe) if and only if all its places are binary.

21 Formalism of Petri Nets: Properties of a Petri net Almost-alive transition • A transition t of a marked Petri net R 0 is almost-alive if and only if there exists a sequence of firings such that: Alive transition • A transition t of a marked Petri net R 0 is alive if and only if: • R 0 is alive for an initial marking M 0 if and only if all its transitions are alive for this marking M 0 Conformity • A Petri net is conform if it is safe and alive Home state • A Petri net state M’ is said to be a home state for a initial marking M 0 if and only if each marking M” in A(R; M 0), M’ is reachable from M”, i. e.

22 Formalism of Petri Nets: Invariances analysis Consider the vector whose components are the number of occurrences of transitions t in a sequence of firings , this vector is called characteristic vector of and its dimension is equal to the number of transitions of the Petri net The evolutions of all the reachable markings of a Petri net can be then given by the equation below: Or This equation is called the fundamental equation of the Petri net and is also used to verify the marking invariance properties. By multiplying the two members of the equation above with v. T with v∈Zn, the equation below is obtained: The interesting values of the vector v are those who verify that v. T. C=0, therefore the equation fundamental becomes:

23 Stochastic Petri Nets (SPNs) Introduction of the time In a Petri net, the time can be introduced in several levels: • Token: Each token carries a time interval during which it is available to fire a given transition. • Place: The tokens in a place remain there during a time interval depending of the place before being used. • Arc: The tokens go through the arcs going from a place to a transition (or vice versa) in a period of time corresponding to the delay of cross. • Transition: The activity modeled by a transition lasts for a time corresponding to the time required for its execution. The beginning of the activity corresponds to the moment when the transition is enabled and its end corresponds to the end of the firing. A transition has a delay of firing resulting to a random firing. At each timed transition t, one can associate a clock. When t is enabled, the clock is initialized with a value y. y is decremented with a constant speed and when its value is 0, t is fired. • The delay of the firing follows an exponential law:

24 Stochastic Petri Nets (SPNs) Definition of a stochastic Petri net A SPN is defined as: SPN={R, Inh, M 0, λ} Where, • R=<P, T, Pre, Post> is a Petri net • Inh is the application: Inh: P X T�N • M 0 is the initial marking • And λ = λ 1, λ 2, …, λn is the set of firing delays of all the transitions. In such Petri net, the distribution of the firing time of each transition is exponential with a rate λ [T]

25 Stochastic Petri Nets (SPNs) Performance study of a SPN In a SPN, if two transitions t 1 and t 2 with respective rates λ 1 and λ 2 are enabled in M, the probability of firing t 1 before t 2 is given by: In the same way, the probability of firing t 2 before t 1 is: These formula show that the probability of passing from the marking M to a marking M’ is independent of the time spent in M. The stay time in M is: The quantitative analysis of a SPN can be performed by analyzing its associated Markov chain

26 Generalized Stochastic Petri Nets (GSPNs) Definition A GSPN is a SPN with two types of transitions: The timed transitions • Are represented by a hollow rectangle • They are fired with a rate depending on the transition as in SPNs. The immediate transitions • Are represented by a solid rectangle • They are fired as soon as they are enabled, i. e. , there is no waiting time Fig. 5. Timed transition and immediate

27 Generalized Stochastic Petri Nets (GSPNs) Definition A GSPN is characterized by <PN, Tt, Ti, λ > where: • R=<P, T, Pre, Post, Inh, M 0> • Tt ⊆ T is the set of timed transitions (Tt ≠ ∅) • Ti ⊆ T is the set of immediate transitions (Ti ∩ Tt = ∅ and T = Ti ∪ Tt) • λ = (λ 1 , λ 2, …, λ|T|) with λi∈R+ is the firing delay if the transition is temporized, the probability of firing if the transition is immediate In the analysis study of GSPN, only tangible markings are considered (the reachable states set is private of evanescent markings) Fig. 6. Example of a GSPN that modeling one system with two parallel activities

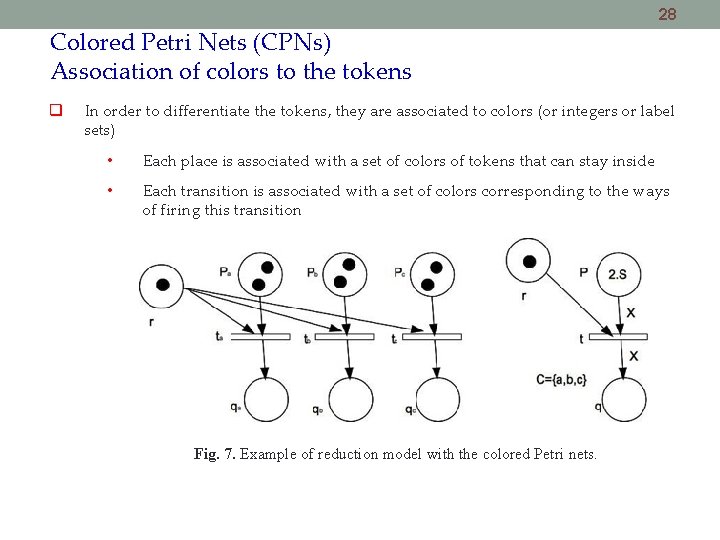
28 Colored Petri Nets (CPNs) Association of colors to the tokens In order to differentiate the tokens, they are associated to colors (or integers or label sets) • Each place is associated with a set of colors of tokens that can stay inside • Each transition is associated with a set of colors corresponding to the ways of firing this transition Fig. 7. Example of reduction model with the colored Petri nets.

29 Colored Petri Nets (CPNs) definition A marked colored Petri net is a 6 -tuples: CPN=<P, T, Ccol, Csec, W, M 0> With: • P = {p 1, p 2, …, pm} is a non-empty finite set of places, • T = {t 1, t 2, …, tn} is a non-empty finite set of transitions, • Ccol = {c 1, c 2, …, cm} is a non-empty finite set of colors, • Csec is the function subset of colors that associates to each place and transition a subset of Ccol: • • W is the incidence function (equivalent of C = Post - Pre), each element W (p, t) of W is itself a function: • • Csec: P ∪ T→Φ (Ccol) where Φ (Ccol) is the set of subsets of Ccol W (p, t): Csec(t) X Csec(p)→N M 0 is the initial marking. For each place and for each possible color in this place, it associates a number of tokens: • M 0(p): Csec(p)→N

30 Well-formed Nets (WNs) definition A well-formed net (WN) is a CPN that respects syntaxic constraints whose major objective is to develop analysis algorithms that can be applied directly on the colored Petri nets. The constraints imposed in this type of network are of three types: • The color areas are cartesian products of basic areas called classes of elementary colors. • The color functions are built from elementary functions that are: the identity, the successor and diffusion. • The model highlights the symmetries of the system. The asymmetric behaviors are considered by partitioning the classes in static subclasses and by adding guards on the color functions and on the transitions.

31 Well-formed Nets (WNs) formalism A WN is defined by the 7 -tuples: WN = <P, T, Cl, C, Pre, Post, Gard> With: • P = {p 1, p 2, …, pm} is a non-empty finite set of places, • T = {t 1, t 2, …, tn} is a non-empty finite set of transitions, • P ∩ T = ∅, • Cl = {Ci|i∈{1, 2, …, k}} is the set of elementary classes. Each Ci is a non-empty finite set that can be partitioned into static subclasses, • C is the colors function P ∪ T → w where subset w is a set containing finite cartesian product of Cl elements. An element of C(s) is a tuple <C 1, C 2, …, Ck> is called color of s. C(s) is the color area of s, • Pre (respectively Post) is the before (respectively back) incidence function which associates to each couple (Px, Ty) of P X T a guarded color function from (Ty) to Bag (C (Px)), • Gard is a function that associates to each transition a guard. By default, Gard (Tx) is the constant function with a value TRUE ∀ Tx∈T.

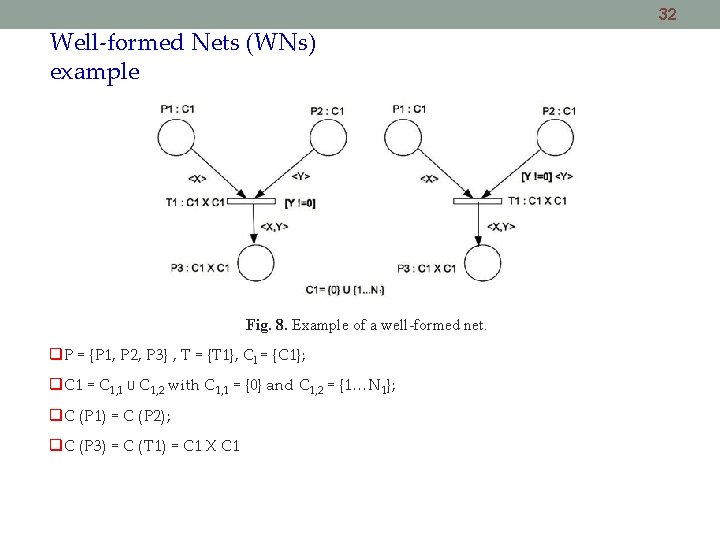
32 Well-formed Nets (WNs) example Fig. 8. Example of a well-formed net. P = {P 1, P 2, P 3} , T = {T 1}, Cl = {C 1}; C 1 = C 1, 1 ∪ C 1, 2 with C 1, 1 = {0} and C 1, 2 = {1…N 1}; C (P 1) = C (P 2); C (P 3) = C (T 1) = C 1 X C 1

33 Stochastic Well-formed Nets (SWNs) definition Introduction of the stochastic character in the WN A stochastic well-formed Petri net (SWN) is a couple S, θ such that: • S = <P, T, Cl, C, Pre, Post, Pri, Gard> is a wellformed Petri net (WN), • θ is a function defined on T such as:

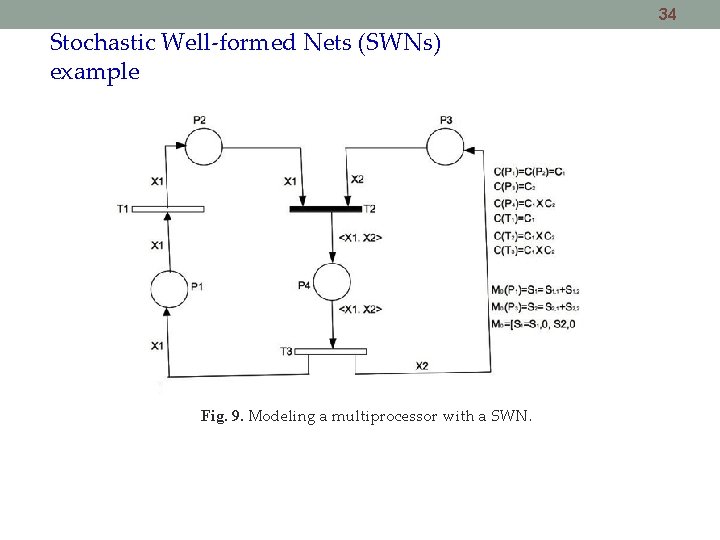
34 Stochastic Well-formed Nets (SWNs) example Fig. 9. Modeling a multiprocessor with a SWN.

35 Conclusion The scientific communities, particularly in the academy and modern industry are faced the need to study the performance of a system before its implementation and even during its functioning Thus, this chapter introduced the fundamental concepts of Petri nets to the researchers and practitioners, Showed how this mathematical and graphical tool has advanced todays in order to be convenient for modeling and analyzing the performance of real complex systems with discrete events that are characterized as being: • concurrent, • synchronous, • asynchronous, • distributed, • parallel, • nondeterministic, and/or stochastic, etc.