Modeling and simulation of brain diffusion MRI Numerical

Modeling and simulation of brain diffusion MRI Numerical simulation and macroscopic model formulation for diffusion magnetic resonance imaging in the brain Jing-Rebecca Li Equipe DEFI, CMAP, Ecole Polytechnique Institut national de recherche en informatique et en automatique (INRIA) Saclay, France L' HABILITATION À DIRIGER DES RECHEHERCHES French-Vietnam Master in Applied Mathematics, Sept 23, 2017 1

Modeling and simulation of brain diffusion MRI De. FI Houssem Haddar Simona Schiavi (Ph. D) Gabrielle Fournet (Ph. D) Dang Van Nguyen (Ph. D) Julien Coatleven (Post-doc) Fabien Caubet (Post-doc) Denis Le Bihan Cyril Poupon Luisa Ciobanu Khieu Van Nguyen (Ph. D) Hang Tuan Nguyen (Ph. D) Master 2 interns Vu Duc Thach Son (April-August 2017), Hoang An Tran (April-August 2016), Hoang Trong An Tran (April-August 2015), Thi Minh Phuong Nguyen (April-August 2014), Khieu Van Nguyen (April 2013 - Aug 2013), Tri Tinh Nguyen (March 2011 - July 2011), Thong Nguyen (March 2011 - July 2011), Cesar Retamal Bravo (March 2007 - July 2007), Sonia Fliss (Sept. 2004 - Mar. 2005). French-Vietnam Master in Applied Mathematics, Sept 23, 2017 2

Modeling and simulation of brain diffusion MRI Outline 1. Brain micro-structure is complex 2. MRI using “diffusion encoding” to “see” micro-structure 3. DMRI signal due to tissue (neurons+other cells) a) Full-scale numerical simulation b) Macroscopic model formulation via homogenization c) Experimental validation in simpler organism French-Vietnam Master in Applied Mathematics, Sept 23, 2017 3

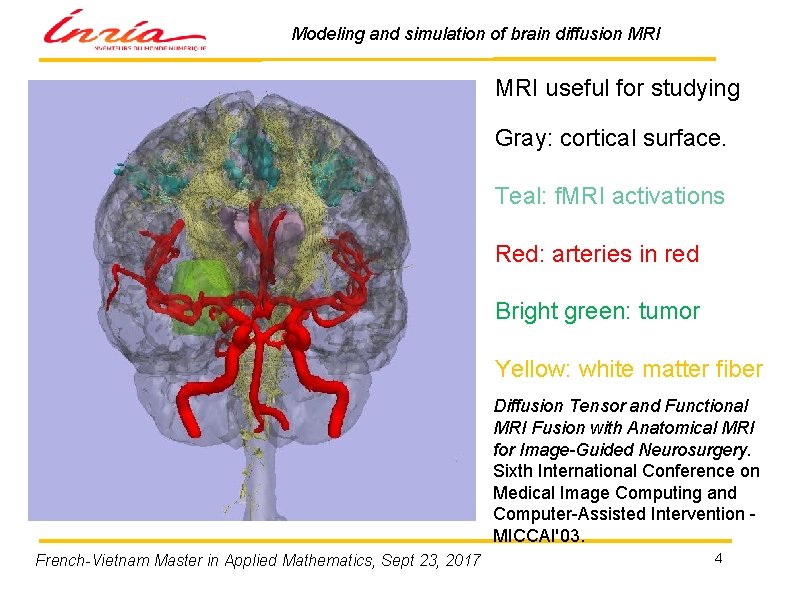
Modeling and simulation of brain diffusion MRI useful for studying Gray: cortical surface. Teal: f. MRI activations Red: arteries in red Bright green: tumor Yellow: white matter fiber Diffusion Tensor and Functional MRI Fusion with Anatomical MRI for Image-Guided Neurosurgery. Sixth International Conference on Medical Image Computing and Computer-Assisted Intervention MICCAI'03. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 4

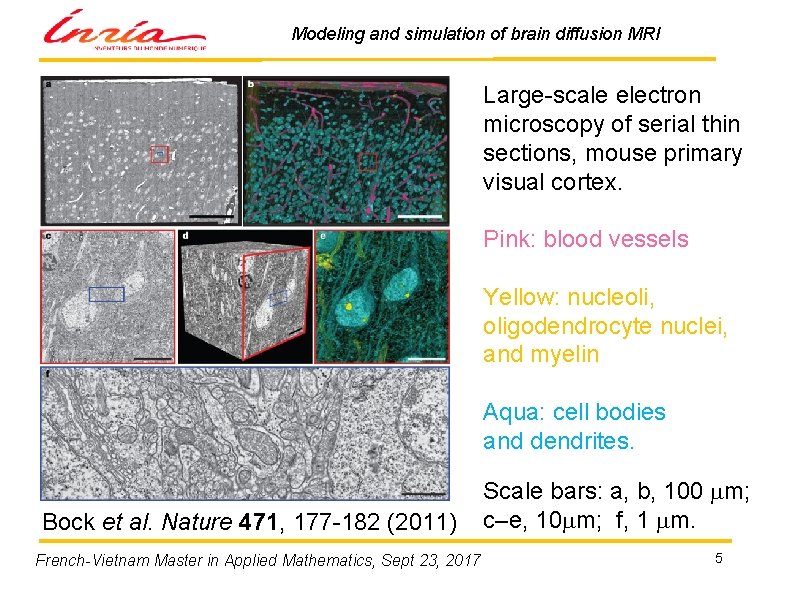
Modeling and simulation of brain diffusion MRI Large-scale electron microscopy of serial thin sections, mouse primary visual cortex. Pink: blood vessels Yellow: nucleoli, oligodendrocyte nuclei, and myelin Aqua: cell bodies and dendrites. Bock et al. Nature 471, 177 -182 (2011) French-Vietnam Master in Applied Mathematics, Sept 23, 2017 Scale bars: a, b, 100 mm; c–e, 10 mm; f, 1 mm. 5

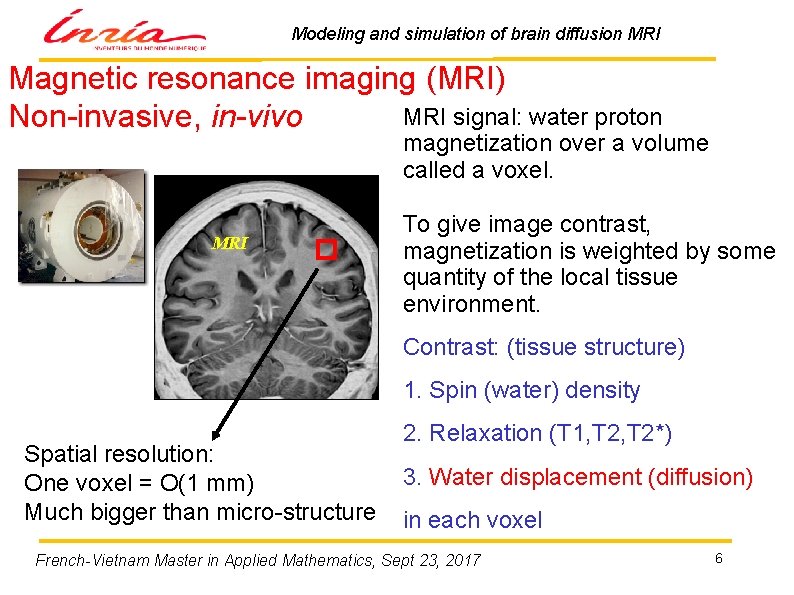
Modeling and simulation of brain diffusion MRI Magnetic resonance imaging (MRI) MRI signal: water proton Non-invasive, in-vivo magnetization over a volume called a voxel. MRI To give image contrast, magnetization is weighted by some quantity of the local tissue environment. Contrast: (tissue structure) 1. Spin (water) density Spatial resolution: One voxel = O(1 mm) Much bigger than micro-structure 2. Relaxation (T 1, T 2*) 3. Water displacement (diffusion) in each voxel French-Vietnam Master in Applied Mathematics, Sept 23, 2017 6

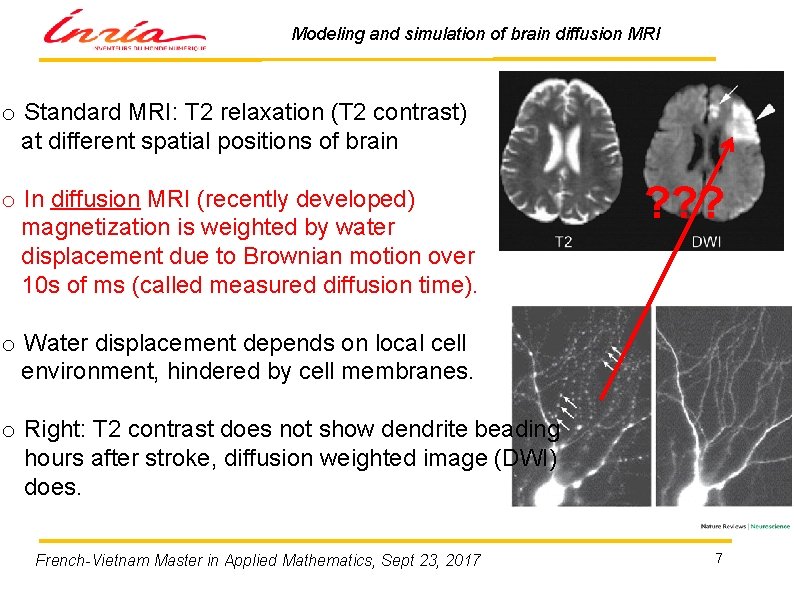
Modeling and simulation of brain diffusion MRI o Standard MRI: T 2 relaxation (T 2 contrast) at different spatial positions of brain o In diffusion MRI (recently developed) magnetization is weighted by water displacement due to Brownian motion over 10 s of ms (called measured diffusion time). ? ? ? o Water displacement depends on local cell environment, hindered by cell membranes. o Right: T 2 contrast does not show dendrite beading hours after stroke, diffusion weighted image (DWI) does. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 7

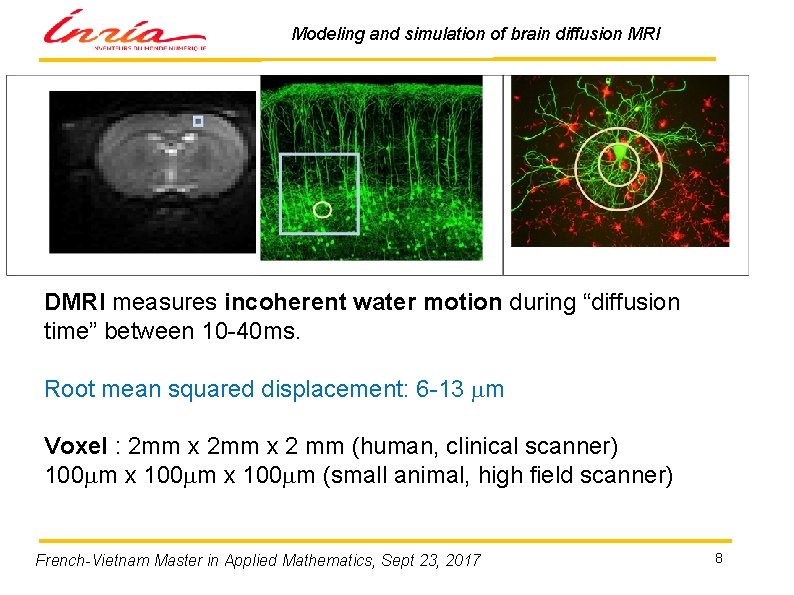
Modeling and simulation of brain diffusion MRI DMRI measures incoherent water motion during “diffusion time” between 10 -40 ms. Root mean squared displacement: 6 -13 mm Voxel : 2 mm x 2 mm (human, clinical scanner) 100 mm x 100 mm (small animal, high field scanner) French-Vietnam Master in Applied Mathematics, Sept 23, 2017 8

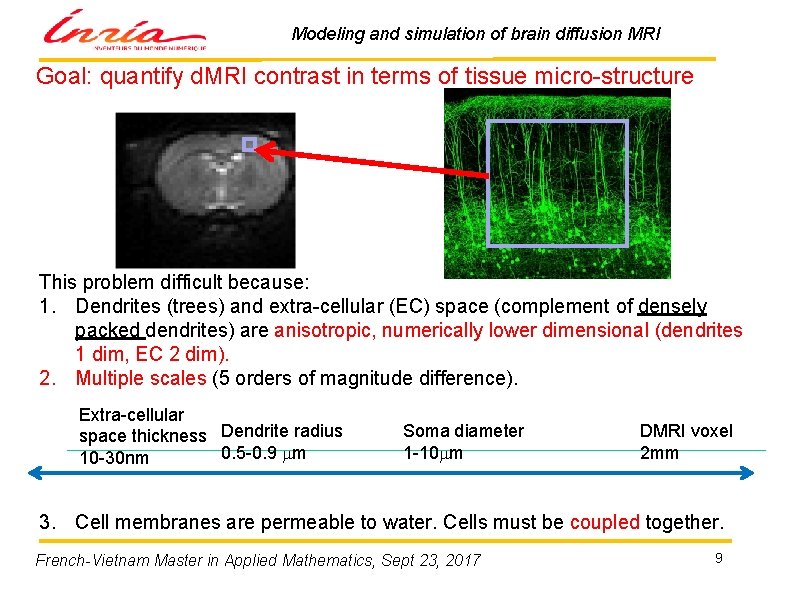
Modeling and simulation of brain diffusion MRI Goal: quantify d. MRI contrast in terms of tissue micro-structure This problem difficult because: 1. Dendrites (trees) and extra-cellular (EC) space (complement of densely packed dendrites) are anisotropic, numerically lower dimensional (dendrites 1 dim, EC 2 dim). 2. Multiple scales (5 orders of magnitude difference). Extra-cellular space thickness Dendrite radius 0. 5 -0. 9 mm 10 -30 nm Soma diameter 1 -10 mm DMRI voxel 2 mm 3. Cell membranes are permeable to water. Cells must be coupled together. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 9

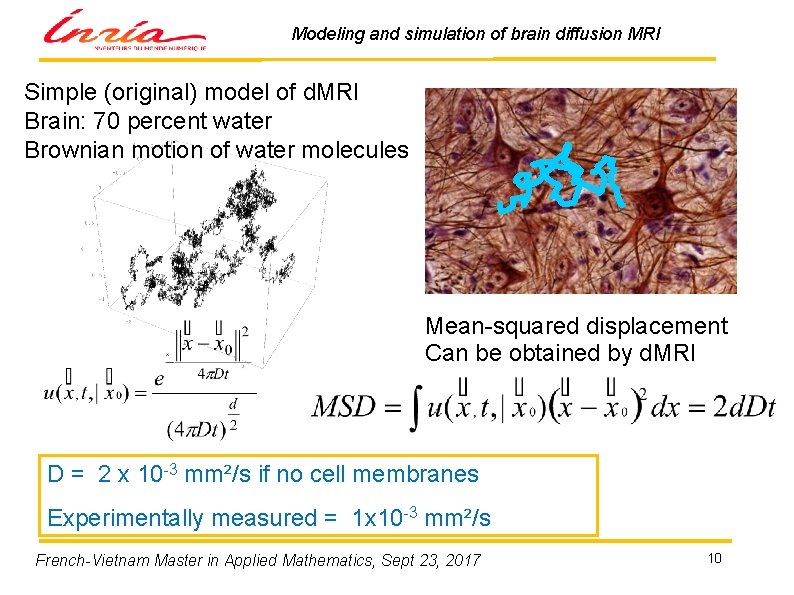
Modeling and simulation of brain diffusion MRI Simple (original) model of d. MRI Brain: 70 percent water Brownian motion of water molecules Mean-squared displacement Can be obtained by d. MRI D = 2 x 10 -3 mm²/s if no cell membranes Experimentally measured = 1 x 10 -3 mm²/s French-Vietnam Master in Applied Mathematics, Sept 23, 2017 10

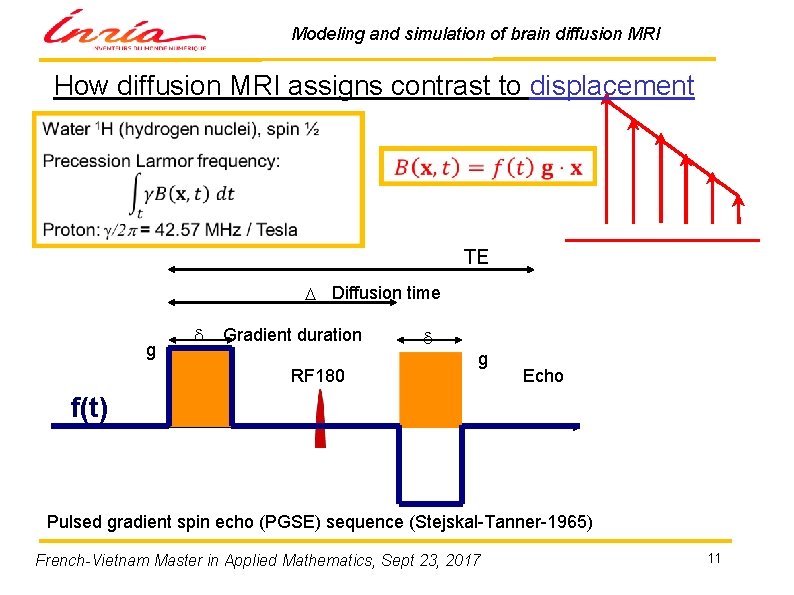
Modeling and simulation of brain diffusion MRI How diffusion MRI assigns contrast to displacement TE D Diffusion time g d Gradient duration RF 180 d g Echo f(t) Pulsed gradient spin echo (PGSE) sequence (Stejskal-Tanner-1965) French-Vietnam Master in Applied Mathematics, Sept 23, 2017 11

Modeling and simulation of brain diffusion MRI French-Vietnam Master in Applied Mathematics, Sept 23, 2017 12

Modeling and simulation of brain diffusion MRI MSD = ADC*(2 D) Brain gray matter: ADC around 10 -3 mm²/s Root MSD: 6 -13 mm French-Vietnam Master in Applied Mathematics, Sept 23, 2017 13

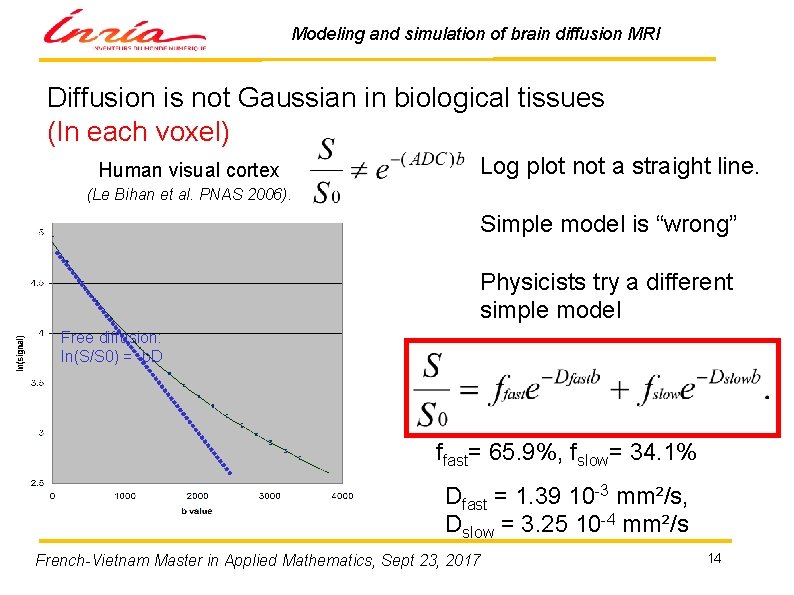
Modeling and simulation of brain diffusion MRI Diffusion is not Gaussian in biological tissues (In each voxel) Human visual cortex Log plot not a straight line. (Le Bihan et al. PNAS 2006). Simple model is “wrong” Physicists try a different simple model Free diffusion: ln(S/S 0) = -b. D ffast= 65. 9%, fslow= 34. 1% Dfast = 1. 39 10 -3 mm²/s, Dslow = 3. 25 10 -4 mm²/s French-Vietnam Master in Applied Mathematics, Sept 23, 2017 14

Modeling and simulation of brain diffusion MRI DMRI signal due to tissue (neurons+other cells) A. Direct simulation of reference model (Bloch-Torrey PDE) o Finite elements + RKC time stepping (Ph. D Dang Van Nguyen) B. Asymptotic models using homogenization C. Experimental validation in simpler organism: Aplysia French-Vietnam Master in Applied Mathematics, Sept 23, 2017 15

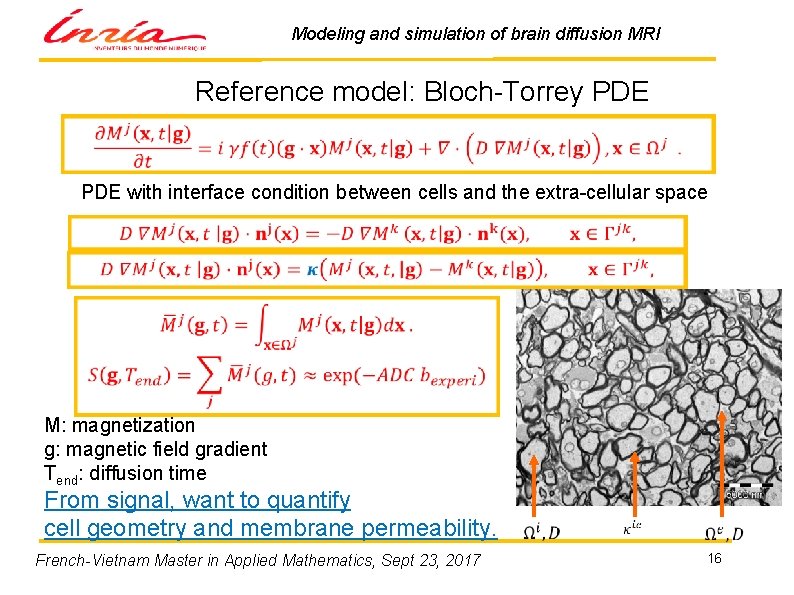
Modeling and simulation of brain diffusion MRI Reference model: Bloch-Torrey PDE with interface condition between cells and the extra-cellular space M: magnetization g: magnetic field gradient Tend: diffusion time From signal, want to quantify cell geometry and membrane permeability. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 16

Modeling and simulation of brain diffusion MRI 1. Numerical simulation of diffusion MRI signals using an adaptive timestepping method, J. -R. Li, D. Calhoun, C. Poupon, D. Le Bihan. Physics in Medicine and Biology, 2013. 2. A finite elements method to solve the Bloch-Torrey equation applied to diffusion magnetic resonance imaging, D. V. Nguyen, J. R. Li, D. Grebenkov, D. Le Bihan, Journal of Computational Physics, 2014. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 17

Modeling and simulation of brain diffusion MRI To do: Define/segment -- mesh – solve Bloch-Torrey PDE on realistic brain tissue geometry French-Vietnam Master in Applied Mathematics, Sept 23, 2017 18

Modeling and simulation of brain diffusion MRI Asymptotic models of d. MRI using periodic homogenization 1. Coupled ODE model Works for large diffusion displacement and wide range of gradient amplitudes. (Post-doc Coatleven, Ph. D Hang Tuan Nguyen) 2. Simpler PDE model for wide range of diffusion displacement and low gradient amplitudes (ADC). (Ph. D. Schiavi) Both are limited to low membrane permeability French-Vietnam Master in Applied Mathematics, Sept 23, 2017 19

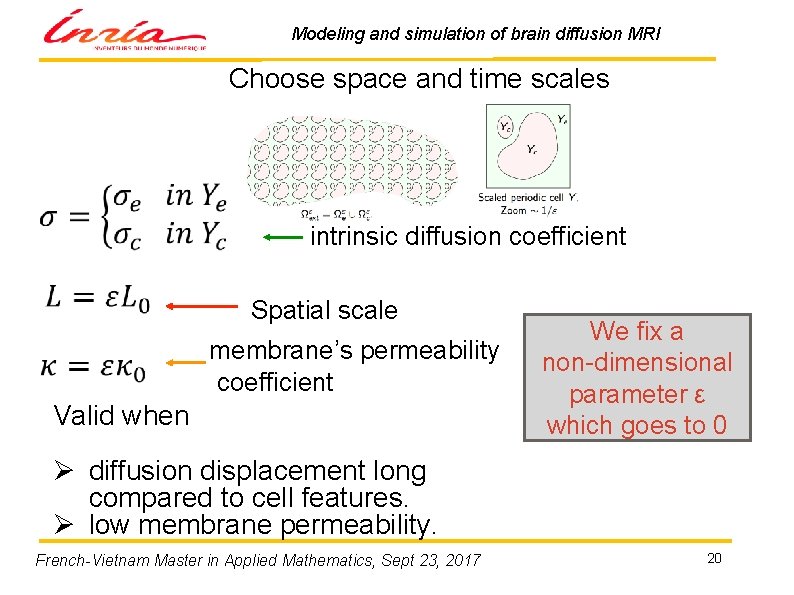
Modeling and simulation of brain diffusion MRI Choose space and time scales intrinsic diffusion coefficient Spatial scale membrane’s permeability coefficient Valid when We fix a non-dimensional parameter ε which goes to 0 Ø diffusion displacement long compared to cell features. Ø low membrane permeability. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 20

Modeling and simulation of brain diffusion MRI Define two space scales: coarse and fine scales And expand magnetization in terms of Match powers (0, 1, 2) of using the PDE, get relationships between coefficient functions French-Vietnam Master in Applied Mathematics, Sept 23, 2017 21

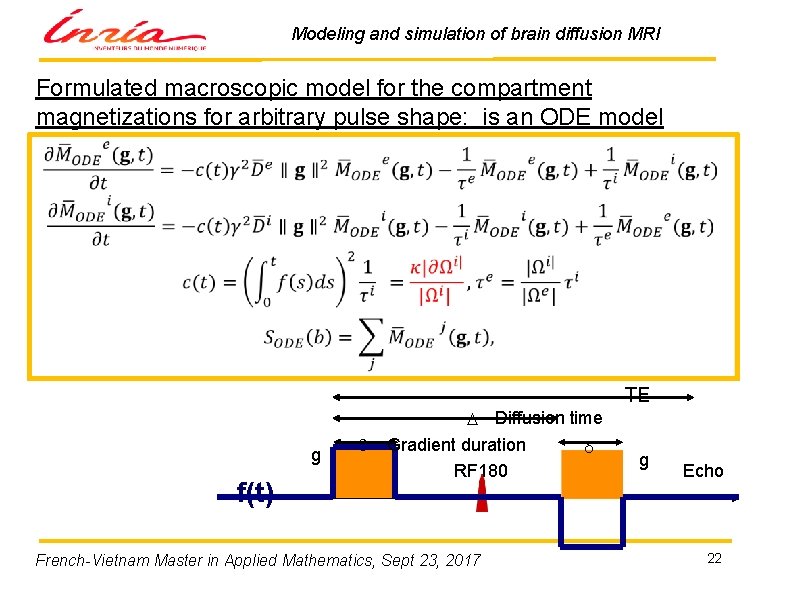
Modeling and simulation of brain diffusion MRI Formulated macroscopic model for the compartment magnetizations for arbitrary pulse shape: is an ODE model TE g f(t) d D Diffusion time Gradient duration d RF 180 French-Vietnam Master in Applied Mathematics, Sept 23, 2017 g Echo 22

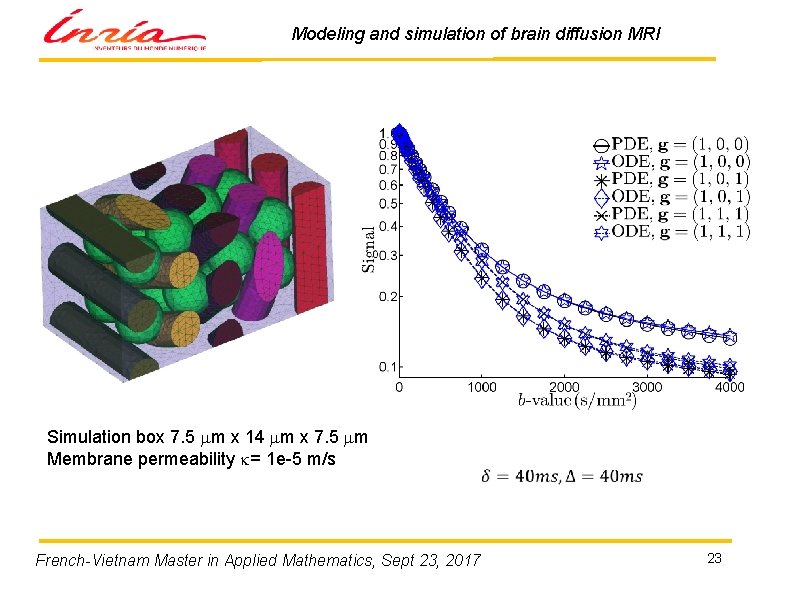
Modeling and simulation of brain diffusion MRI Simulation box 7. 5 mm x 14 mm x 7. 5 mm Membrane permeability k= 1 e-5 m/s French-Vietnam Master in Applied Mathematics, Sept 23, 2017 23

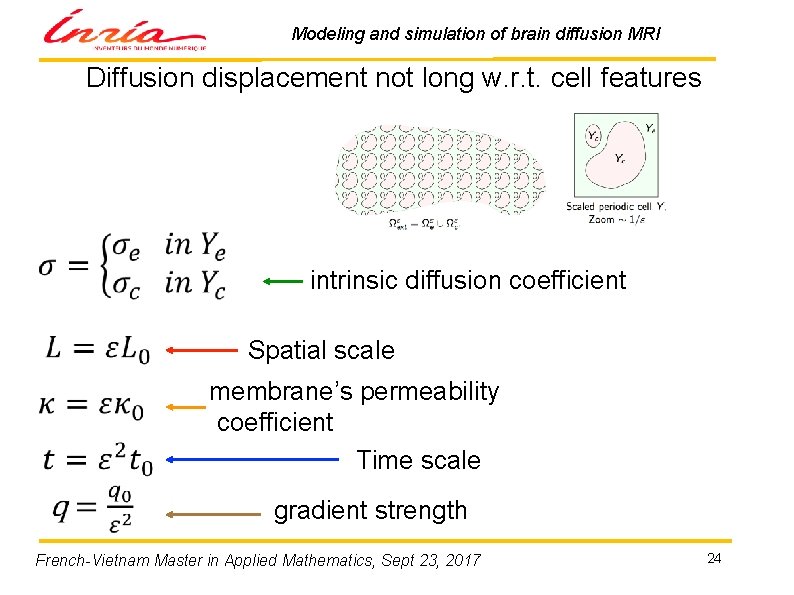
Modeling and simulation of brain diffusion MRI Diffusion displacement not long w. r. t. cell features intrinsic diffusion coefficient Spatial scale membrane’s permeability coefficient Time scale gradient strength French-Vietnam Master in Applied Mathematics, Sept 23, 2017 24

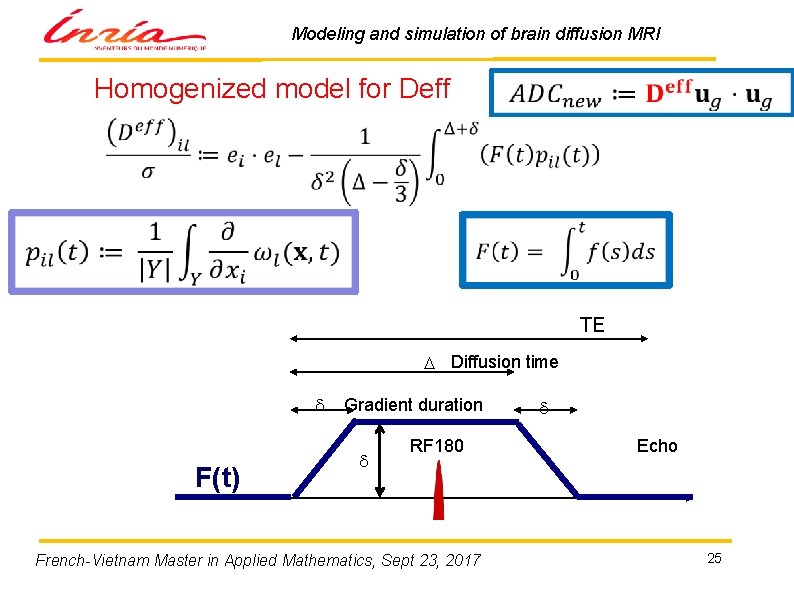
Modeling and simulation of brain diffusion MRI Homogenized model for Deff TE D Diffusion time d F(t) Gradient duration d RF 180 French-Vietnam Master in Applied Mathematics, Sept 23, 2017 d Echo 25

Modeling and simulation of brain diffusion MRI Homogenized model for Deff Homogeneous diffusion equation with constant coefficient and Neumann boundary condition on the interface French-Vietnam Master in Applied Mathematics, Sept 23, 2017 26

Modeling and simulation of brain diffusion MRI French-Vietnam Master in Applied Mathematics, Sept 23, 2017 27

Modeling and simulation of brain diffusion MRI French-Vietnam Master in Applied Mathematics, Sept 23, 2017 28

Modeling and simulation of brain diffusion MRI French-Vietnam Master in Applied Mathematics, Sept 23, 2017 29

Modeling and simulation of brain diffusion MRI French-Vietnam Master in Applied Mathematics, Sept 23, 2017 30

Modeling and simulation of brain diffusion MRI Homogenized model for Deff French-Vietnam Master in Applied Mathematics, Sept 23, 2017 31

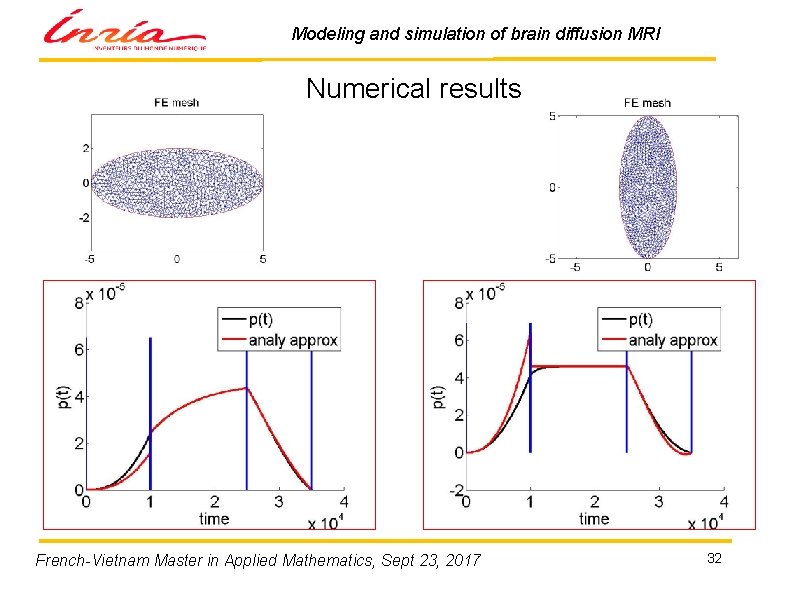
Modeling and simulation of brain diffusion MRI Numerical results French-Vietnam Master in Applied Mathematics, Sept 23, 2017 32

Modeling and simulation of brain diffusion MRI To do: Ø Model is not so simple like ODE, must work to simplify it to make it numerically efficient for parameter estimation. Ø Use mix of layer potentials and eigenfunctions Ø Account for multiple scales and anisotropic shape of neurons. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 33

Modeling and simulation of brain diffusion MRI Estimating cell size and membrane permeability using reference PDE model in neuron network of the Aplysia (sea slug). (Ph. D. Khieu Van Nguyen) Cells are really big. French-Vietnam Master in Applied Mathematics, Sept 23, 2017 34

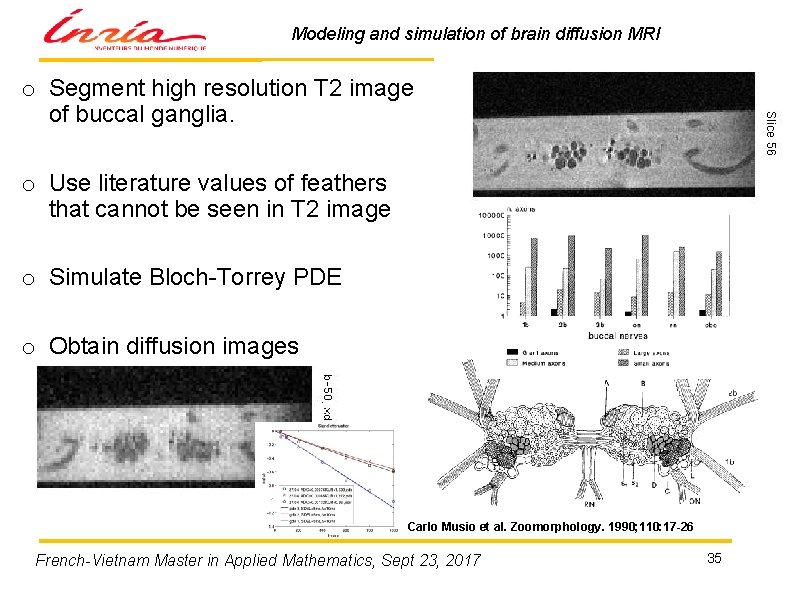
Modeling and simulation of brain diffusion MRI o Segment high resolution T 2 image of buccal ganglia. o Use literature values of feathers that cannot be seen in T 2 image o Simulate Bloch-Torrey PDE o Obtain diffusion images Carlo Musio et al. Zoomorphology. 1990; 110: 17 -26 French-Vietnam Master in Applied Mathematics, Sept 23, 2017 35

Modeling and simulation of brain diffusion MRI Thank you for your attention! French-Vietnam Master in Applied Mathematics, Sept 23, 2017 36