Modeling and Advanced Control Design for DCDC Converters

Modeling and Advanced Control Design for DC/DC Converters in Microgrids Chris Leonard and Baylor Howard Advisor: Dr. Jing Wang Department of Electrical and Computer Engineering Bradley University May 4, 2019

Outline ● ● ● Introduction ○ Project Background ○ Problem Statement ○ Objectives Modeling ○ Basic Circuit ○ Switch ON/OFF ○ Averaged State Space Model Control Design Simulation ○ Linear Model ○ Nonlinear Model Conclusion References 2

Introduction 3

Problem Background ● Renewable energy accounts for 11% ○ Solar: 6% of renewables (0. 66% overall) ■ Source: US Energy Information Administration ● Microgrids are used in off-grid locations ● Many DC/DC converters and DC/AC inverters are in Microgrids ○ ○ For load and needs of feeding to main grid Ensuring MPPT Figure 1 PV Microgrid Block Diagram ● It is of importance to develop advanced control algorithms to ensure the steady output of converters in the presence of model uncertainties and input perturbations. 4

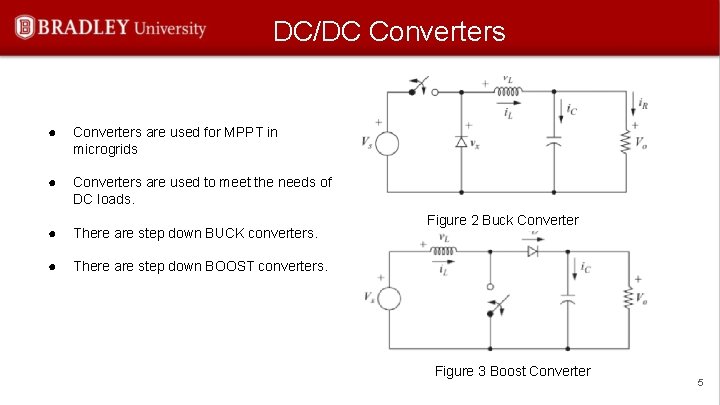
DC/DC Converters ● Converters are used for MPPT in microgrids ● Converters are used to meet the needs of DC loads. ● There are step down BUCK converters. ● There are step down BOOST converters. Figure 2 Buck Converter Figure 3 Boost Converter 5

Project Objectives ● Modeling Analysis ○ Study the averaged state space model ● Develop advanced control algorithms for DC/DC converter ○ ○ Linear Design Nonlinear Design ● Functional Requirements ○ ○ ○ The proposed design will be non-model based (not relying on system parameters). The proposed PWM control signal is ensured to be in the range of duty cycle. The proposed control can handle input perturbation (robustness) The proposed control can handle load uncertainty. The proposed control is robust to existing ESRs for inductors and capacitors. 6

Modeling 7

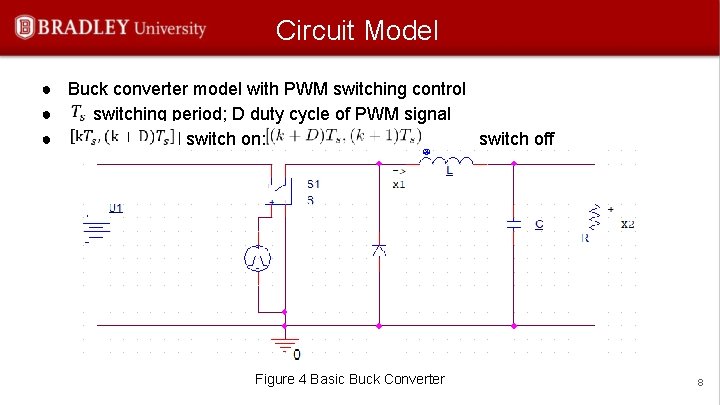
Circuit Model ● Buck converter model with PWM switching control ● Ts switching period; D duty cycle of PWM signal ● [k. Ts, (k+D)Ts] switch on; [k+D)Ts, (k+1)Ts) switch off Figure 4 Basic Buck Converter 8

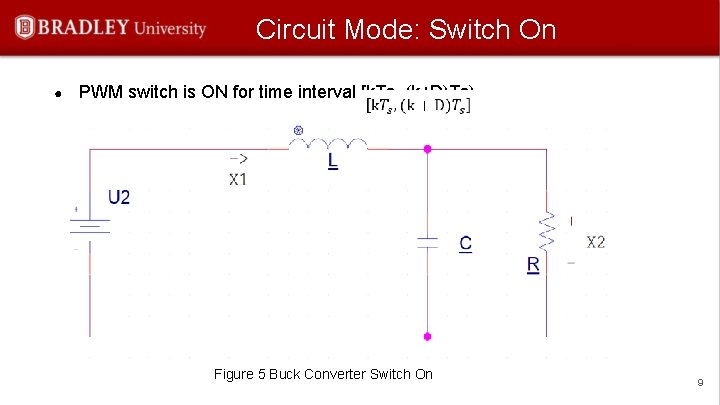
Circuit Mode: Switch On ● PWM switch is ON for time interval [k. Ts, (k+D)Ts) Figure 5 Buck Converter Switch On 9

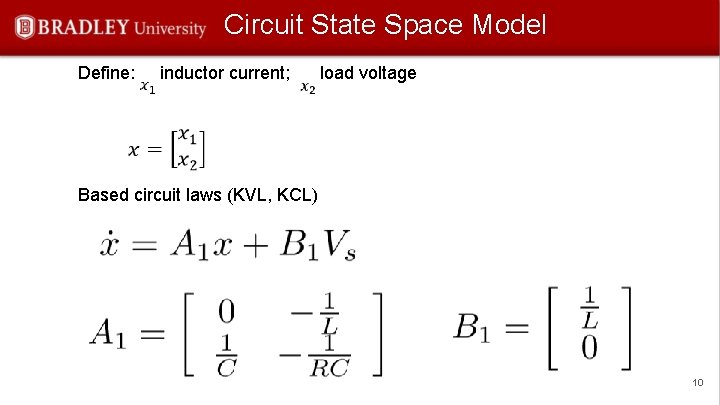
Circuit State Space Model Define: inductor current; load voltage Based circuit laws (KVL, KCL) 10

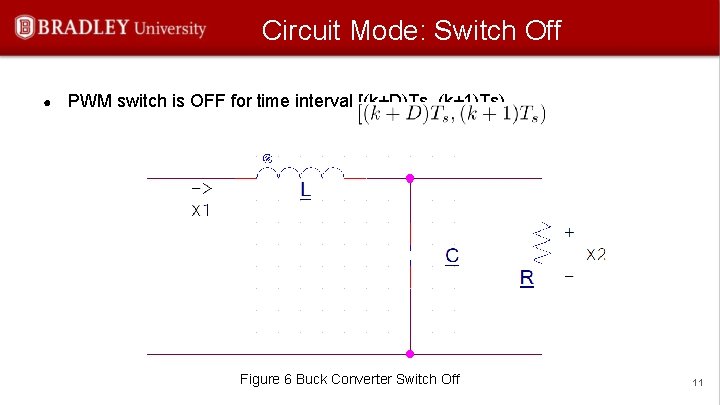
Circuit Mode: Switch Off ● PWM switch is OFF for time interval [(k+D)Ts, (k+1)Ts) Figure 6 Buck Converter Switch Off 11

Circuit State Space Model ● Time Interval ● State Equation ● A and B matrix 12

Averaged State Space Model ● The input to RLC circuit behaves like a square wave signal with frequency ● If Ts is small enough, a Fourier analysis can show that the circuit output is dominated by the DC component of a square wave signal. ● Thus, the following averaged state space model is used for control design. 13

Control Design 14

Linear Design ● The design is based on linearization around the equilibrium point of the system. ● Let the desired output voltage be ● The equilibrium point is ● Define error signals ● Linearized model is 15

Linear Design ● The control is ● Gain matrix K can be obtained using pole placement method. 16

Linear Design ● The possible issues with linear design ○ ○ ○ Model based; need know system parameters L, C, R If there are uncertainties, control gain K obtained from nominal values may not render stable poles any more. The obtained control ΔD may be out of range for duty cycle, and the proper scaling has to be used. 17

Nonlinear Design ● The proposed new control is ● Stability analysis can be done using Lyapunov direct method. 18

Nonlinear Design ● Lyapunov function ● We can show that its derivative along the system trajectory ● Which ensure e 1 goes to zero and e 2 goes to zero. 19

Nonlinear Design ● The benefits using this new design ○ ○ Nonlinear model based; robustness to systems uncertainties Control input is guaranteed in the range of [0, 1]; no scaling factor needed. ● Simulation study ○ ○ Input perturbation Load change 20

Simulation 21

Simulation ● Parameters ○ L 1 = 1. 33 m. H ○ C 1 = 94 u. F ○ R 1 = 4 Ω ○ Vin = 42, 44 V ○ Vout = 12 V ○ D = 12/42 ○ Ts = 0. 01 ms Figure 7 MATLAB Square Wave 22

Linear Design Figure 8 Linear Pspice Model 23

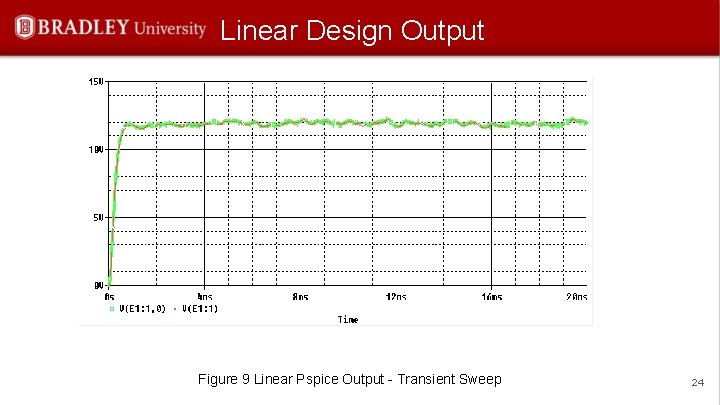
Linear Design Output Figure 9 Linear Pspice Output - Transient Sweep 24

Linear Design Output Linear model with load change at R=4[�� ] at 5% tolerance with n=50 samples Figure 10 Linear Pspice Output - Monte Carlo 25

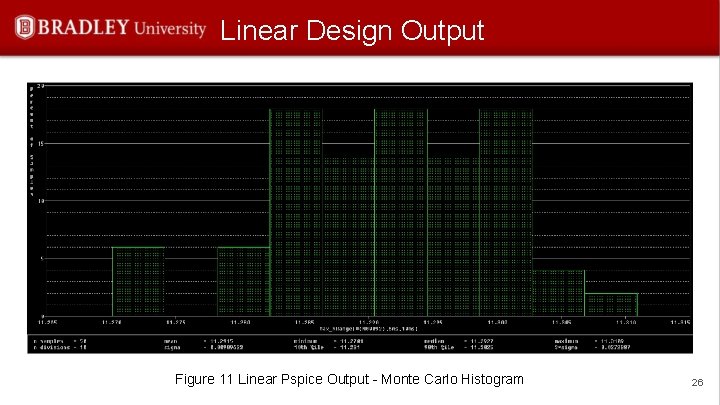
Linear Design Output Figure 11 Linear Pspice Output - Monte Carlo Histogram 26

Nonlinear Model Figure 12 Nonlinear Pspice Model 27

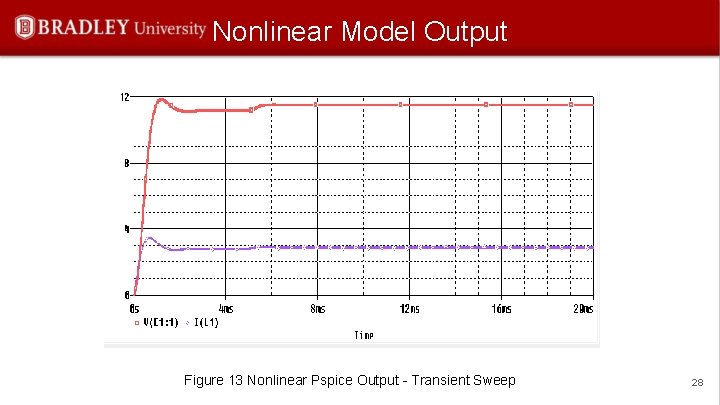
Nonlinear Model Output Figure 13 Nonlinear Pspice Output - Transient Sweep 28

Nonlinear Model Output Nonlinear model with load change in R=4[�� ] at 5% tolerance with n=50 samples Figure 14 Nonlinear Pspice Output - Monte Carlo 29

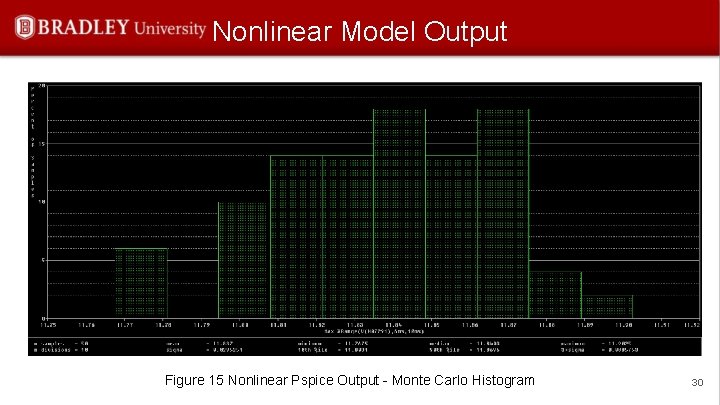
Nonlinear Model Output Figure 15 Nonlinear Pspice Output - Monte Carlo Histogram 30

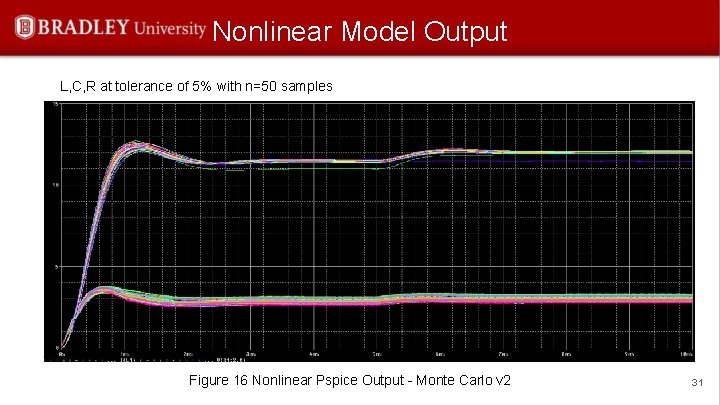
Nonlinear Model Output L, C, R at tolerance of 5% with n=50 samples Figure 16 Nonlinear Pspice Output - Monte Carlo v 2 31

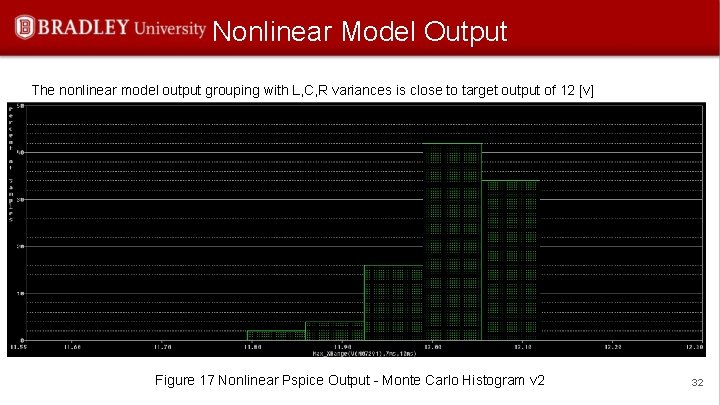
Nonlinear Model Output The nonlinear model output grouping with L, C, R variances is close to target output of 12 [v] Figure 17 Nonlinear Pspice Output - Monte Carlo Histogram v 2 32

Cost ● Used MATLAB & Pspice ○ Available resources in lab ● TMS 320 C 2000 Digital Power Kit ○ $200 ○ Two channel DC/DC buck converter Figure 18 TMS 320 C 2000 33

Division of Labor ● Chris ○ PSpice modeling ○ Controls theory application ○ State space model design ○ Physical buck converter attempt ● Baylor ○ DC/DC converter modeling ■ MATLAB & Pspice ○ Linear model of system ○ Simulation testing ○ H-Bridge inverter work 34

Conclusion ● Due to the environmental impact of finite fossil fuels on our atmosphere, it is imperative that we take the necessary steps towards sustainable energy sources such as solar power. ● This project thoroughly studied the control techniques and strategies for DC/DC converters, namely strategies for linear and nonlinear control of buck and boost converters. ● The simulation results which were obtained verify the effectiveness of the proposed converter design. ● Once implemented, our system will be able to improve power efficiency within microgrids due to it’s precise variable input tracking. 35

Future Work ● Implement system with H-Bridge Inverter ● Use C 2000 MCU ● 3 -phase power ● Battery storage ● PV panel efficiency Figure 19 C 2000 MCU 36

References 1. Y. Lu, “Advanced grid-tied photovoltaic micro-inverter”, University of Canterbury, Christchurch, New Zealand, 2015. 1. Texas Instruments, “Digitally controlled solar micro inverter design using C 2000 Piccolo microcontroller, ” TIDU 405 B datasheet, Oct. 2014 [Revised June 2017]. 1. D. Hart, “Power Electronics. ” New York: Mc. Graw-Hill, 2011. 37