Modeling a Chronic Disease Model and a Mental

Modeling a Chronic Disease Model and a Mental Health Model Using the Same Modeling Tools Jacob Barhak Freelancer Austin, Texas H. Stephen Leff Harvard Medical School Cambridge, Massachusetts

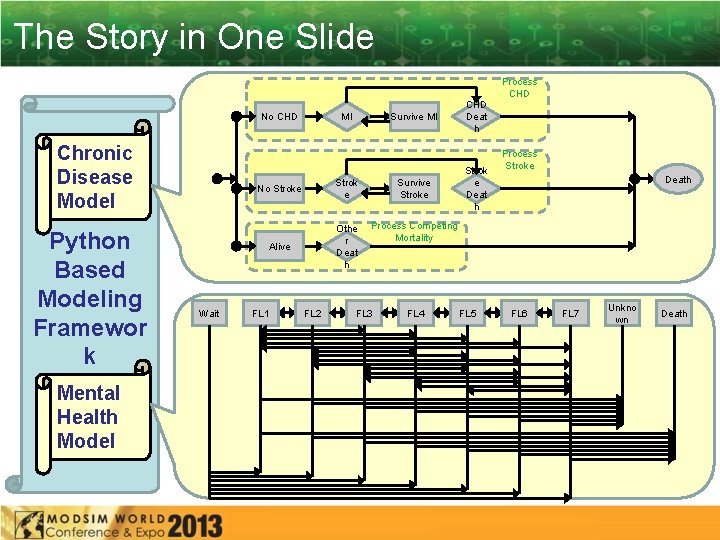
The Story in One Slide No CHD Chronic Disease Model Python Based Modeling Framewor k Mental Health Model Wait Survive MI MI No Stroke Strok e Survive Stroke Alive Othe r Deat h Process Competing Mortality FL 1 FL 2 FL 3 FL 4 CHD Deat h Strok e Deat h FL 5 Process CHD Process Stroke Death FL 6 FL 7 Unkno wn Death

Why it is Important? • Currently Physical and Mental Health are modeled separately • Physical and Mental Health interact and influence each other • Integrated physical and mental health care called for in the Affordable Care Act • Model Implementations currently use different environments • Implementing both models in the same environment is a first step towards: – Merging both models – Improved modeling capabilities – Modeling interactions between processes

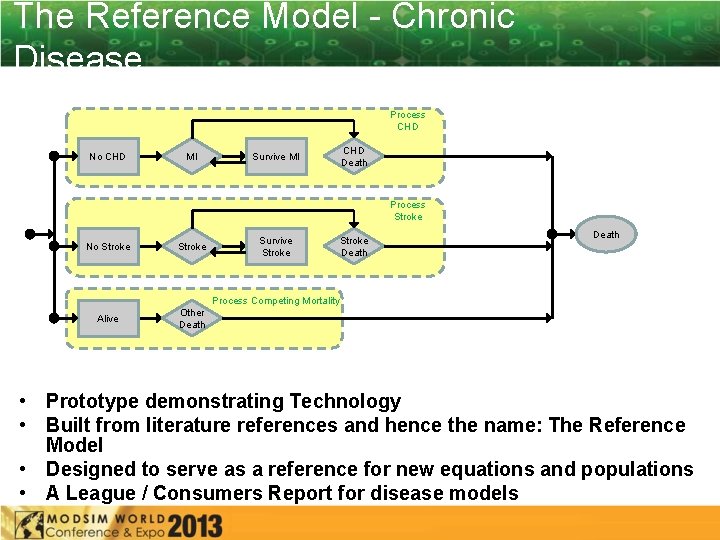
The Reference Model - Chronic Disease Process CHD No CHD MI CHD Death Survive MI Process Stroke No Stroke Alive Other Death Survive Stroke Death Process Competing Mortality • Prototype demonstrating Technology • Built from literature references and hence the name: The Reference Model • Designed to serve as a reference for new equations and populations • A League / Consumers Report for disease models

The Reference Model Key Features • Simple - Low Resolution • Based on secondary data: – Published Risk Equations – Published Clinical Trials, i. e. no real individual data – Other publications • Relies on computing power/techniques – Parallel processing / High Performance Computing – Competition among alternative equation/hypothesis combinations – Cross validation - One click validation – Ranks results according to fitness - Fitness Engine – Accumulates knowledge

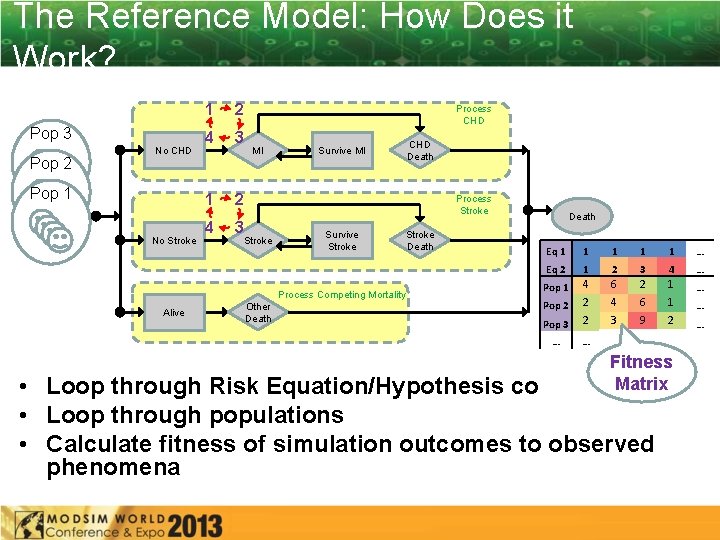
The Reference Model: How Does it Work? Pop 3 Pop 2 No CHD Pop 1 No Stroke 1 2 4 3 1 2 4 Process CHD MI CHD Death Survive MI Process Stroke 3 Stroke Survive Stroke Death Process Competing Mortality Alive Other Death Eq 1 1 1 … Eq 2 1 2 3 4 … Pop 1 4 6 2 1 … Pop 2 2 4 6 1 … Pop 3 2 3 9 2 … … … … Fitness Matrix combinations • Loop through Risk Equation/Hypothesis • Loop through populations • Calculate fitness of simulation outcomes to observed phenomena

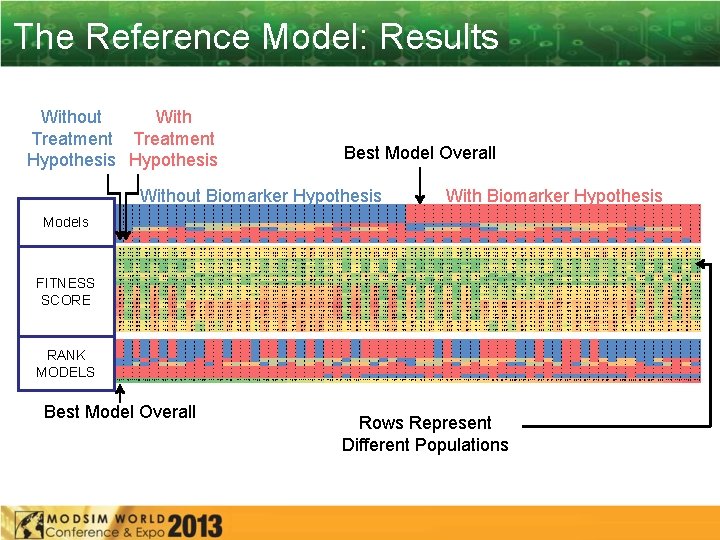
The Reference Model: Results Without With Treatment Hypothesis A 1 c changes BMI changes BP changes Lipid change Smoke changes MI Equation # Stroke Equation # CHD Death Equation # Stroke Death Equation # Treatment Improvement Correction FITNESS: LOW SCORE = GOOD FITNESS UKPDS 33 Conventional UKPDS 33 Intensive UKPDS 33 Full ASPEN All Placebo ASPEN All Atorvastatin ASPEN Primary Placebo ASPEN Primary Atorvastatin ASPEN Secondary Placebo ASPEN Secondary Atorvastatin ASPEN Full ADVANCE Standard ADVANCE Intensive ADVANCE Asia Standard ADVANCE Asia Intensive ADVANCE EME Standard ADVANCE EME Intensive ADVANCE Eastern Europe Standard ADVANCE Eastern Europe Intensive ADVANCE Full ACCORD BP Standard Therapy ACCORD BP Intensive Therapy ACCORD BP Full Models FITNESS SCORE OVERALL MODEL RANKING RESULTS Method_A 1 c Method_BMI Method_BP Method_Lipids Method_Smoke Method_MI Method_Stroke Method_Death. CHD Method_Death. Stroke Method_Time. Improve Weighted Mean RANK MODELS Best Model Overall Without Biomarker Hypothesis 0 0 0 1 1 1 0 0 0 1 2 1 1 1 0 0 0 1 3 1 1 1 0 0 0 1 4 1 1 1 0 0 0 2 1 1 0 0 0 2 2 1 1 1 0 0 0 2 3 1 1 1 0 0 0 2 4 1 1 1 0 0 0 3 1 1 0 0 0 3 2 1 1 1 0 0 0 3 3 1 1 1 0 0 0 3 4 1 1 0 27. 0 24. 6 21. 5 14. 3 18. 5 23. 3 21. 7 23. 2 16. 2 8. 3 67. 3 66. 7 72. 6 84. 8 91. 2 75. 9 78. 5 57. 3 46. 8 42. 5 43. 9 24. 1 22. 5 23. 0 10. 2 9. 4 9. 5 13. 1 37. 6 18. 8 11. 8 9. 9 12. 1 18. 9 21. 2 14. 0 21. 6 15. 7 10. 8 12. 7 30. 4 27. 9 24. 6 21. 4 21. 3 13. 8 20. 5 23. 1 24. 3 21. 2 10. 3 7. 9 54. 0 59. 3 58. 4 64. 4 80. 4 83. 0 71. 0 69. 2 54. 9 48. 0 46. 7 45. 4 31. 7 26. 3 9. 7 10. 2 11. 1 11. 4 39. 7 20. 9 13. 4 10. 4 12. 8 17. 0 17. 5 20. 4 27. 4 19. 5 17. 5 14. 6 27. 9 28. 6 29. 2 24. 6 22. 4 10. 2 17. 6 22. 3 21. 7 21. 9 12. 2 7. 6 60. 1 62. 7 64. 5 71. 2 79. 7 82. 4 69. 1 73. 6 55. 4 54. 3 49. 8 53. 0 33. 1 30. 1 29. 9 10. 2 11. 3 9. 0 10. 3 40. 4 29. 0 13. 1 16. 0 14. 8 12. 2 18. 0 26. 4 30. 3 21. 5 19. 6 18. 3 35. 1 32. 7 34. 0 26. 9 24. 2 23. 6 15. 1 15. 8 20. 6 22. 9 21. 0 11. 6 8. 2 62. 7 60. 3 70. 9 79. 4 81. 1 87. 1 70. 8 75. 8 57. 0 53. 0 48. 9 51. 8 31. 2 26. 5 29. 5 10. 6 8. 0 9. 0 11. 9 37. 3 20. 7 9. 7 12. 8 14. 5 13. 2 17. 3 22. 4 28. 3 17. 1 16. 2 12. 7 32. 0 29. 2 29. 3 43. 0 37. 0 35. 1 15. 9 22. 7 19. 7 25. 0 22. 7 14. 8 9. 8 36. 6 42. 7 35. 2 32. 8 75. 6 82. 3 65. 6 66. 3 52. 7 41. 5 43. 5 44. 3 24. 6 31. 9 29. 5 21. 9 28. 4 31. 5 32. 1 6. 2 18. 5 17. 3 24. 1 23. 6 21. 5 24. 5 49. 2 45. 7 41. 2 44. 2 38. 8 21. 5 15. 1 17. 7 42. 5 34. 1 34. 5 13. 5 22. 6 25. 4 23. 0 19. 0 13. 1 10. 3 27. 5 34. 5 26. 8 32. 7 67. 9 74. 9 59. 7 61. 1 52. 5 44. 7 41. 6 43. 2 32. 7 35. 2 39. 4 22. 0 28. 5 26. 7 32. 7 11. 6 20. 7 17. 9 22. 8 27. 2 20. 5 23. 2 51. 7 57. 0 48. 0 47. 7 44. 8 24. 1 24. 2 25. 3 36. 3 35. 6 35. 1 17. 8 18. 7 24. 6 24. 2 20. 5 15. 3 9. 4 31. 0 36. 4 29. 2 37. 8 65. 9 70. 5 58. 1 56. 1 53. 9 50. 6 48. 4 49. 1 35. 8 38. 2 37. 3 18. 1 30. 0 31. 3 31. 2 17. 7 27. 5 19. 5 27. 2 25. 3 23. 9 52. 9 58. 5 48. 7 49. 2 48. 1 34. 7 31. 7 34. 8 39. 2 34. 3 19. 0 21. 6 23. 0 25. 5 18. 1 13. 2 9. 0 32. 9 37. 6 32. 6 37. 3 65. 1 75. 3 55. 9 59. 3 53. 3 49. 5 43. 4 50. 1 33. 4 34. 0 33. 8 22. 1 29. 9 27. 8 31. 6 11. 9 23. 6 20. 1 25. 0 28. 9 19. 9 26. 7 49. 7 56. 0 42. 8 45. 1 46. 6 29. 0 28. 2 39. 7 32. 2 31. 5 12. 5 16. 8 15. 5 17. 2 18. 4 25. 9 9. 4 54. 1 59. 1 53. 0 58. 9 79. 4 79. 0 62. 9 69. 5 53. 1 62. 6 54. 4 58. 9 29. 4 40. 8 37. 1 23. 5 26. 0 23. 8 25. 2 15. 7 40. 1 16. 6 39. 4 47. 0 43. 5 49. 5 55. 1 57. 2 44. 9 51. 9 50. 2 32. 3 35. 3 33. 6 39. 7 32. 5 32. 0 12. 6 15. 4 14. 3 15. 6 13. 6 23. 0 5. 6 48. 0 51. 3 48. 3 53. 9 66. 9 76. 3 57. 1 57. 8 56. 4 63. 3 55. 9 60. 4 36. 9 43. 3 42. 4 18. 7 25. 2 22. 6 25. 7 15. 4 39. 2 15. 7 42. 2 48. 9 43. 6 52. 4 57. 7 66. 0 56. 7 53. 2 51. 7 39. 1 36. 5 41. 2 39. 6 34. 3 33. 6 10. 9 16. 6 16. 0 17. 4 14. 6 24. 3 7. 6 50. 1 53. 4 52. 4 56. 5 70. 0 72. 9 51. 4 55. 0 52. 5 66. 3 63. 6 64. 3 46. 2 45. 7 45. 9 18. 2 29. 5 21. 7 26. 2 24. 4 46. 6 13. 7 52. 4 53. 5 47. 4 54. 1 59. 0 63. 8 51. 2 57. 0 54. 9 49. 3 47. 7 35. 9 29. 6 34. 2 12. 1 13. 9 15. 8 16. 5 12. 8 24. 2 8. 0 49. 9 56. 2 53. 1 57. 5 72. 4 73. 9 51. 6 54. 4 54. 3 63. 5 60. 3 63. 3 1 0 1 0 1 0 1 0 0 0 1 0 1 0 0 0 1 1 1 4 1 1 2 1 4 2 3 2 4 4 1 1 1 1 1 1 1 18. 51 18. 92 19. 78 20. 04 20. 51 20. 72 20. 73 20. 92 21. 48 21. 66 Best Model Overall 1 1 0 1 1 0 4 4 4 1 4 3 1 1 1 1 1 22. 5 22. 63 22. 88 0 0 0 3 4 1 1 1 With Biomarker Hypothesis 0 0 0 4 1 1 1 0 0 0 4 2 1 1 0 0 0 4 2 1 1 1 0 0 0 4 3 1 1 1 0 0 0 4 4 1 1 1 0 1 1 1 1 2 1 1 0 1 1 1 2 1 1 1 1 1 3 1 1 0 1 1 1 3 1 1 1 1 1 4 1 1 0 1 1 1 4 1 1 1 1 2 1 1 1 0 1 1 1 2 1 1 1 1 1 2 2 1 1 0 1 1 1 2 2 1 1 1 1 2 3 1 1 0 1 1 1 2 3 1 1 1 1 2 4 1 1 0 1 1 1 2 4 1 1 1 1 3 1 1 1 0 1 1 1 3 1 1 1 1 1 3 2 1 1 0 1 1 1 3 2 1 1 1 1 3 3 1 1 0 1 1 1 3 3 1 1 1 1 3 4 1 1 0 1 1 1 3 4 1 1 1 1 4 1 1 1 0 1 1 1 4 1 1 1 1 1 4 2 1 1 0 1 1 1 4 2 1 1 1 1 4 3 1 1 0 1 1 1 4 3 1 1 1 1 4 4 1 1 0 1 1 1 4 4 1 1 1 38. 1 34. 6 41. 8 42. 4 42. 5 43. 8 19. 3 23. 2 28. 8 21. 7 33. 3 25. 7 34. 7 16. 2 20. 9 42. 7 20. 8 17. 4 18. 9 43. 4 65. 4 50. 8 73. 2 47. 0 67. 2 52. 9 79. 7 61. 4 89. 0 65. 4 100. 6 50. 0 81. 8 49. 3 79. 0 55. 1 64. 6 42. 4 52. 8 39. 8 47. 5 41. 1 49. 9 22. 7 21. 6 21. 9 12. 5 9. 8 13. 1 45. 7 26. 2 14. 8 12. 9 9. 8 23. 3 16. 9 16. 0 23. 8 16. 2 13. 8 37. 0 33. 8 35. 1 35. 8 41. 4 39. 7 22. 4 25. 1 31. 3 31. 4 13. 8 19. 3 18. 8 60. 5 63. 9 70. 7 82. 2 86. 4 72. 2 72. 7 61. 4 49. 4 44. 3 48. 2 27. 8 25. 6 27. 9 13. 4 11. 8 10. 2 10. 5 47. 3 26. 4 16. 3 10. 1 8. 5 21. 0 14. 3 19. 8 17. 1 22. 2 19. 1 12. 8 36. 2 32. 2 34. 4 33. 7 42. 6 22. 9 28. 9 29. 9 32. 2 19. 4 19. 3 17. 3 67. 6 67. 9 67. 1 74. 4 87. 3 92. 6 76. 2 78. 8 64. 5 54. 4 56. 8 51. 8 30. 4 30. 6 32. 3 13. 5 12. 1 9. 0 10. 0 50. 7 33. 1 16. 2 12. 3 11. 6 12. 2 7. 6 24. 5 20. 6 20. 8 21. 0 13. 1 38. 3 37. 6 34. 4 41. 7 25. 1 29. 0 32. 7 16. 6 20. 6 19. 7 60. 2 70. 2 66. 7 75. 2 81. 5 89. 3 70. 2 68. 4 66. 2 52. 5 52. 0 56. 2 29. 8 29. 5 28. 7 13. 4 10. 1 9. 3 10. 4 48. 1 26. 0 15. 3 11. 0 11. 6 11. 7 7. 7 20. 8 18. 1 22. 5 16. 7 13. 6 36. 2 34. 9 36. 0 23. 6 22. 8 23. 7 15. 5 15. 0 23. 4 17. 0 22. 7 12. 0 8. 2 45. 9 40. 4 54. 4 45. 3 64. 3 61. 4 54. 0 43. 5 39. 6 46. 5 36. 7 43. 5 24. 7 22. 7 21. 6 10. 3 9. 4 8. 7 11. 3 37. 9 21. 9 10. 6 9. 8 21. 2 18. 7 11. 1 11. 9 20. 4 19. 3 15. 8 30. 0 28. 7 28. 4 25. 0 22. 4 22. 5 14. 5 12. 8 21. 3 15. 7 21. 1 7. 6 10. 1 40. 1 37. 6 42. 2 42. 6 58. 7 54. 7 47. 9 39. 9 35. 5 47. 7 37. 2 42. 2 29. 0 28. 1 9. 0 10. 6 9. 8 10. 7 36. 3 24. 7 13. 7 7. 2 7. 1 19. 3 15. 3 17. 7 19. 5 17. 6 16. 8 11. 6 28. 5 29. 2 30. 1 25. 5 22. 4 21. 9 12. 3 12. 8 20. 8 16. 5 19. 5 12. 5 10. 4 43. 5 39. 2 47. 3 42. 2 64. 6 57. 3 48. 5 40. 9 38. 2 46. 9 43. 6 48. 0 33. 0 28. 6 29. 6 9. 3 11. 3 9. 0 9. 8 39. 7 28. 3 13. 7 9. 1 8. 4 12. 4 10. 7 21. 5 18. 2 19. 0 15. 1 10. 9 34. 8 31. 4 34. 2 26. 7 22. 0 23. 0 14. 5 9. 1 22. 4 16. 0 20. 2 14. 2 9. 3 44. 0 41. 8 48. 7 41. 8 62. 0 56. 1 38. 0 37. 6 50. 9 41. 3 46. 2 33. 1 29. 0 27. 6 9. 9 8. 7 9. 1 12. 0 38. 7 25. 9 12. 4 9. 6 8. 8 11. 1 9. 7 19. 1 19. 5 16. 6 14. 2 7. 2 31. 9 32. 3 30. 3 40. 4 34. 6 35. 6 13. 7 17. 1 23. 4 21. 6 24. 8 10. 3 11. 0 27. 7 30. 3 22. 3 29. 9 64. 2 70. 2 52. 6 52. 9 45. 3 42. 2 36. 1 39. 6 24. 7 33. 7 30. 0 21. 1 22. 3 30. 1 24. 9 7. 9 13. 0 19. 8 18. 1 20. 2 22. 7 21. 9 41. 8 40. 1 34. 9 36. 1 36. 6 20. 0 13. 9 16. 9 39. 9 31. 6 33. 8 17. 5 17. 8 24. 3 21. 4 19. 2 7. 3 10. 2 24. 6 25. 7 23. 8 25. 8 60. 7 66. 8 46. 0 51. 6 47. 3 41. 7 36. 9 40. 6 30. 3 32. 6 34. 5 25. 7 26. 9 30. 5 26. 7 10. 2 11. 8 17. 3 19. 6 18. 8 20. 2 20. 4 45. 8 46. 7 39. 7 37. 8 40. 6 23. 1 20. 8 22. 3 40. 3 32. 0 36. 3 14. 6 15. 8 23. 5 22. 0 20. 9 11. 2 9. 0 26. 9 31. 1 24. 0 25. 5 62. 4 61. 0 45. 7 48. 0 45. 0 49. 3 40. 6 46. 0 34. 2 38. 3 37. 4 21. 1 24. 9 29. 5 26. 8 18. 2 21. 7 17. 3 23. 7 23. 1 20. 2 19. 1 50. 2 47. 1 43. 8 39. 1 42. 1 31. 7 28. 4 31. 1 38. 6 33. 2 37. 5 16. 7 16. 0 26. 5 24. 0 18. 3 11. 7 8. 9 29. 6 28. 7 24. 2 28. 8 59. 7 64. 4 46. 3 44. 5 48. 7 48. 3 45. 1 44. 4 30. 4 36. 1 34. 5 22. 5 23. 1 31. 1 28. 6 11. 5 16. 8 16. 6 23. 2 24. 8 22. 2 21. 5 43. 4 48. 7 40. 5 43. 0 40. 2 28. 8 28. 7 27. 1 37. 7 34. 0 34. 1 13. 7 14. 9 14. 6 15. 6 18. 7 21. 3 7. 6 45. 2 40. 2 42. 5 47. 0 65. 6 62. 3 49. 9 47. 6 44. 0 58. 3 44. 2 52. 4 33. 7 39. 4 37. 7 21. 6 24. 6 25. 1 22. 0 16. 0 30. 5 16. 0 37. 6 31. 6 37. 7 35. 1 46. 9 43. 9 36. 0 35. 2 37. 7 28. 8 25. 5 30. 5 36. 0 34. 2 33. 9 11. 4 13. 3 16. 1 15. 9 13. 8 18. 1 7. 2 34. 7 34. 3 39. 1 59. 1 54. 0 46. 9 44. 7 45. 7 56. 0 46. 9 51. 7 35. 0 45. 7 44. 8 24. 3 23. 8 25. 1 23. 8 18. 2 31. 8 13. 4 33. 6 38. 7 41. 4 37. 7 49. 7 46. 0 44. 6 37. 9 46. 6 39. 6 31. 9 34. 9 40. 2 32. 9 36. 4 12. 3 14. 5 15. 0 13. 3 14. 9 22. 3 8. 0 40. 9 36. 5 44. 5 38. 5 57. 2 56. 3 48. 9 38. 8 47. 4 63. 1 53. 3 57. 5 41. 1 47. 3 19. 1 21. 2 21. 5 23. 5 25. 8 37. 0 15. 7 40. 5 40. 7 34. 8 38. 6 53. 7 49. 1 45. 3 35. 7 45. 3 45. 7 35. 9 39. 2 38. 6 32. 3 34. 3 14. 5 15. 6 17. 3 15. 1 13. 6 20. 9 10. 1 41. 6 39. 1 41. 0 45. 3 61. 1 58. 7 42. 1 43. 6 44. 7 60. 7 54. 6 57. 5 37. 6 45. 0 41. 0 23. 4 21. 3 24. 4 18. 3 35. 7 16. 3 37. 7 37. 2 35. 4 40. 1 55. 1 49. 9 41. 7 41. 1 46. 5 43. 0 34. 9 38. 6 35. 8 43. 4 42. 6 22. 0 17. 0 29. 4 23. 1 23. 2 11. 7 18. 7 50. 7 52. 0 48. 5 50. 8 74. 1 68. 8 60. 6 62. 4 46. 5 45. 9 30. 7 37. 4 22. 3 21. 9 23. 3 14. 6 11. 8 9. 4 11. 8 46. 9 29. 9 16. 7 19. 9 12. 8 25. 8 22. 5 19. 0 17. 1 29. 1 25. 2 19. 0 38. 9 38. 3 40. 0 38. 4 42. 9 40. 5 24. 0 16. 5 31. 1 25. 4 14. 9 6. 1 14. 2 40. 7 45. 8 48. 0 49. 4 67. 9 60. 4 56. 2 52. 2 44. 8 47. 0 37. 8 37. 6 29. 3 27. 4 28. 3 13. 3 12. 8 10. 2 10. 3 49. 7 29. 3 18. 2 15. 5 12. 6 21. 9 19. 9 21. 0 20. 6 27. 2 21. 5 13. 2 37. 2 35. 7 37. 5 34. 3 44. 1 45. 1 20. 8 18. 4 32. 7 23. 2 17. 3 9. 2 17. 9 50. 2 47. 7 51. 4 56. 6 70. 0 63. 5 57. 1 55. 8 48. 3 52. 5 41. 2 44. 2 33. 2 31. 2 28. 7 12. 8 11. 9 8. 8 8. 7 48. 1 34. 8 16. 0 14. 4 11. 5 17. 5 9. 7 20. 5 16. 8 26. 0 20. 7 13. 3 38. 6 39. 2 40. 3 34. 3 43. 7 41. 2 20. 9 17. 9 32. 2 22. 0 18. 0 10. 2 16. 8 45. 1 46. 6 55. 2 56. 6 64. 4 64. 7 53. 9 54. 5 51. 9 54. 0 40. 8 47. 9 31. 0 27. 5 27. 4 13. 9 11. 8 7. 9 8. 5 47. 4 32. 9 15. 7 13. 7 12. 4 14. 7 11. 9 19. 0 17. 9 26. 1 24. 1 13. 6 38. 1 39. 0 39. 3 1 1 0 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 0 1 0 1 1 4 4 1 2 2 2 2 3 1 2 2 3 3 1 2 1 4 2 3 4 2 1 2 3 3 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 23. 2 23. 57 23. 77 25. 67 27. 65 27. 91 30. 56 31. 15 31. 41 32. 09 33. 88 33. 89 34. 14 34. 43 35. 32 35. 69 1 1 1 3 1 1 0 35. 7 1 1 1 1 2 1 1 4 4 1 1 1 1 0 0 0 36. 12 36. 34 1 1 1 3 2 1 1 0 37. 7 1 1 1 3 2 1 1 1 37. 9 0 1 0 0 0 1 1 1 1 0 0 1 0 0 1 1 0 1 0 0 1 0 0 0 1 1 0 2 3 3 2 3 4 3 1 4 4 3 2 4 1 3 4 3 3 4 1 1 2 2 4 1 2 3 4 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 0 0 38. 1 38. 96 39. 15 39. 45 39. 65 39. 92 40. 18 40. 52 40. 76 41. 61 42. 15 42. 85 43. 02 43. 71 44. 55 44. 57 44. 99 45. 38 45. 46 Rows Represent Different Populations 0 0 0 0 0 0 0 1 3 3 1 1 3 3 3 4 1 1 1 0 0 46. 3 46. 87 47. 07 47. 24 47. 62 0 0 0 0 0 0 0 3 4 4 1 2 4 3 1 1 1 0 0 0 47. 7 51. 37 53. 41 55. 47 55. 58

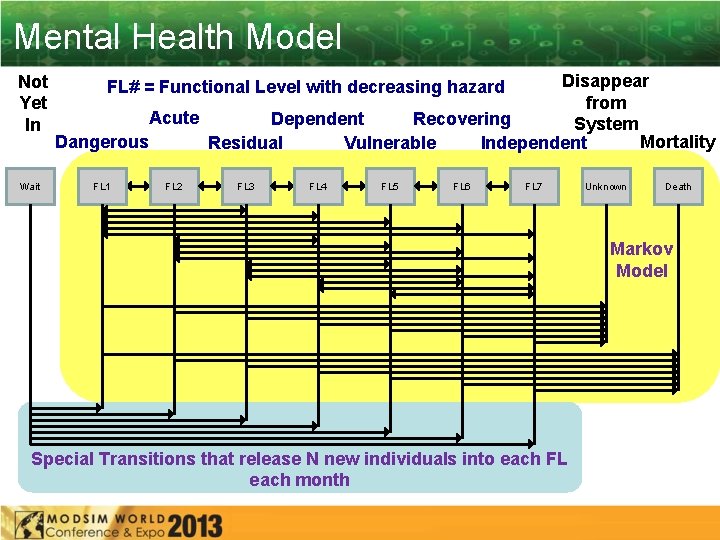
Mental Health Model Not Yet In Wait Disappear from Acute Dependent Recovering System Dangerous Mortality Residual Vulnerable Independent FL# = Functional Level with decreasing hazard FL 1 FL 2 FL 3 FL 4 FL 5 FL 6 FL 7 Unknown Death Markov Model Special Transitions that release N new individuals into each FL each month

Mental Health Model: Markov Model • The Markov Model transitions probabilities used FL 1 FL 2 FL 3 FL 4 FL 5 FL 6 FL 7 Death 0 Unknow n 0. 005 FL 1 0. 624 0. 118 0. 05 0. 154 0. 007 0. 005 FL 2 0. 099 0. 624 0. 129 0. 037 0. 068 0. 002 0 0. 004 0. 037 FL 3 0. 006 0. 031 0. 716 0. 184 0. 022 0. 001 0 0. 003 0. 037 FL 4 0. 019 0. 069 0. 734 0. 111 0. 013 0 0. 003 0. 037 FL 5 0. 004 0. 007 0. 015 0. 073 0. 747 0. 103 0. 013 0. 002 0. 036 FL 6 0 0. 008 0. 05 0. 879 0. 017 0. 001 0. 037 FL 7 0 0 0 1 0 0 Unknow n 0 0 0 0 1 0 Death 0 0 0 0 1 • Transition probabilities out of wait state are conditional if statements: 0. 037 – 0 if Time < Arrival Time for all FL – 1 if Time < Arrival Time and Individual ID corresponds to FL# 9

Mental Health Model: Reimplementation • This Mental Health Model was previously published: – Leff H. S. , Dada M. , Graves S. C. (1986), An LP planning model for a mental health community support system. Management Science 32(2) 139 -155 – Leff, H. S. , Hughes, D. , Chow, C. , Noyes, S. , & Ostrow, L. (2009). A Mental Health Allocation and Planning Simulation Model: A Mental Health Planner's Perspective. In Y. Yuehwern (Ed. ), Handbook of Healthcare Delivery Systems. • The implementation reports: – – – Number of individuals in each state each month Monthly service costs & Total costs Number of transitions forward = improvement Number of transitions backwards = regression Number of individuals staying in the same state 10

Mental Health Model: Reimplementation • The Reimplementation using the Python based Modeling Framework has the following advantages: • Micro-Simulation: – Each individual is modeled separately – Potential to add individual characteristics • Sensitivity Analysis: – Multiple Scenarios were executed – Perturbation as added to transition probabilities • Future benefits: – The Reference Model can be augmented with a mental health process 11

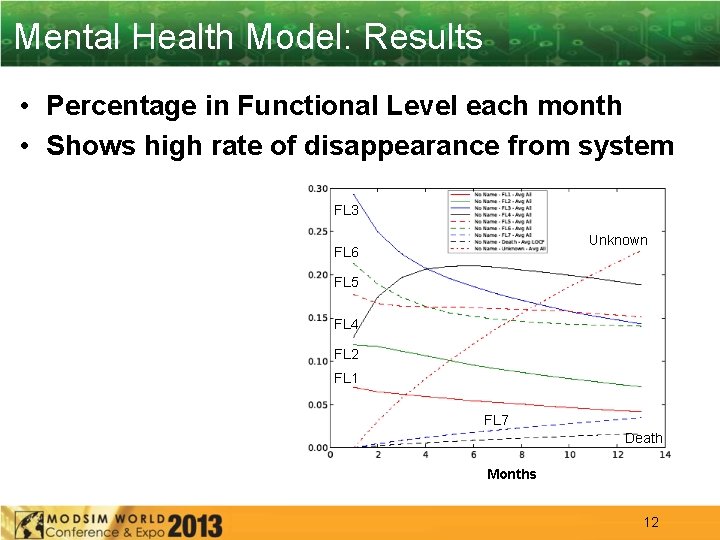
Mental Health Model: Results • Percentage in Functional Level each month • Shows high rate of disappearance from system FL 3 Unknown FL 6 FL 5 FL 4 FL 2 FL 1 FL 7 Death Months 12

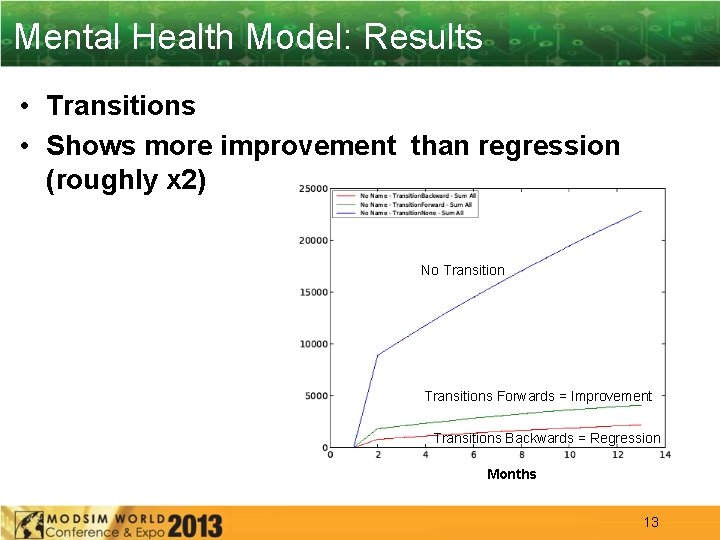
Mental Health Model: Results • Transitions • Shows more improvement than regression (roughly x 2) No Transitions Forwards = Improvement Transitions Backwards = Regression Months 13

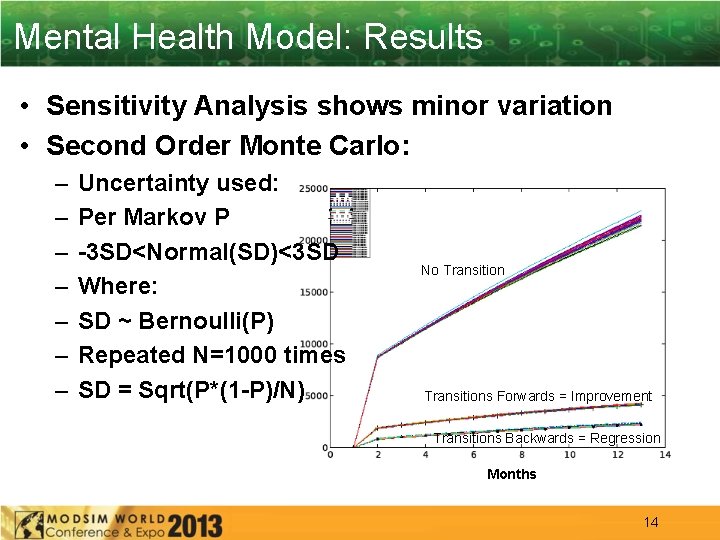
Mental Health Model: Results • Sensitivity Analysis shows minor variation • Second Order Monte Carlo: – – – – Uncertainty used: Per Markov P -3 SD<Normal(SD)<3 SD Where: SD ~ Bernoulli(P) Repeated N=1000 times SD = Sqrt(P*(1 -P)/N) No Transitions Forwards = Improvement Transitions Backwards = Regression Months 14

Quality Control • Models are prone to human error. • The following techniques were used to improve quality: – – – Equations were implemented twice separately Test scripts were written to test implementation Versioning Documentation Human inspection of code and results 15

Summary & Future Work • 1 st step towards merging Mental & Physical Health models • Future modeling work : – Bridge Yearly / Monthly Time Scale gap – Merge Models into one model with different processes – Model interactions between processes – Enhancing Mental Health beyond Markov = Individualized – Multiple Populations/Trials comparison 16

Summary & Future Work • The Modeling Framework itself is being renovated • From IEST (Indirect Estimation and Simulation Tool): – Combines estimation and simulation capabilities – Supports legacy requirements • To MIST (MIcro Simulation Tool): – Simplified – Optimized for simulation – Intended to use recent technological advances 17

Acknowledgments • The GPL modeling framework described above was supported by the Biostatistics and Economic Modeling Core of the MDRTC (P 60 DK 020572) and by the Methods and Measurement Core of the MCDTR (P 30 DK 092926), both funded by the National Institute of Diabetes and Digestive and Kidney Diseases. The modeling framework was initially defined as GPL and was funded by Chronic Disease Modeling for Clinical Research Innovations grant (R 21 DK 075077) from the same institute. • The Reference Model was developed independently without financial support. • The Mental Health Model development was initially supported by National Institute of Mental Health Grant No. IR 01 -MH 33581 -02. Since then it has been supported by funds from various State and County planning projects. The reimplementation of the model described in this paper was not supported financially. 18