Modele drzew autoregresyjnych w analizie szeregw czasowych Wodzimierz

Modele drzew autoregresyjnych w analizie szeregów czasowych Włodzimierz Bielski Na podstawie: C. Meek, D. M. Chickering and D. Heckerman (2002). Autoregressive Tree Models for Time-Series Analysis. In Proceedings of the Second International SIAM Conference on Data Mining, Arlington, VA, pages 229 -244.

Agenda o Przypomnienie pojęć o Część teoretyczna – na podst. artykułu o Część praktyczna – SQL Server 2005

Wprowadzenie o o o Analiza i modelowanie szeregów czasowych jest ważnym obszarem badań w wielu zastosowaniach Rozpatrzymy Auto. Regressive Tree models (ART) Są one połączeniem klasycznej autoregresji i drzewa decyzyjnego Microsoft Research, 2001 Implementacja w Microsoft SQL Server 2005

Proces stochastyczny: definicja o o Funkcja losowa, czyli funkcja której wartości leżą w przestrzeni zdarzeń losowych Pewnej wielkości przypisane jest zdarzenie losowe Przykład: wielokrotny rzut monetą, D=N, f(D) {O, R} Formalnie, proces stochastyczny to rodzina zmiennych losowych , gdzie Xt – zmienna losowa, T – zbiór indeksów

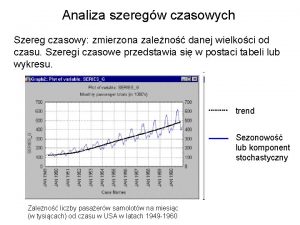
Szeregi czasowe: przypomnienie o o o Serie obserwacji dokonywanych w równych odstępach czasu Inaczej: proces stochastyczny, którego dziedziną jest czas Sprzedaż, kursy walut, notowania giełdowe

Szeregi czasowe: definicja o o o Mamy ciąg zmiennych losowych Szereg czasowy jest ciągiem wartości tych zmiennych Ograniczamy się do modeli szeregów czasowych, które są probabilistyczne, stacjonarne, Markowa rzędu p:

Szeregi czasowe o o o Stacjonarne – zależność yt od poprzednich wartości nie zmienia się w czasie Proces Markowa rzędu p – mając dane p poprzednich obserwacji, yt jest niezależny od reszty wcześniejszych obserwacji Koncentrujemy się więc na modelach postaci Zmienna objaśniana Funkcja regresji Zmienne objaśniające

Autoregresja o o Najbardziej popularny model analizy szeregów czasowych: autoregresja liniowa (AR) Liniowy model autoregresyjny o długości p, ozn. AR(p): wartość oczekiwana - rozklad normalny - parametry modelu

Modele ART o o W AR(p) zawsze jedna formuła regresyjna – istotne ograniczenie Model drzewa autoregresyjnego (ART) – przedziałowy (cząstkowy, piecewise) autoregresyjny model, w którym granice przedziałów są określone przez drzewo decyzyjne, zaś liście zawierają liniowe modele autoregresyjne

Przykład drzewa ART

Przykład drzewa ART o Zmienna Yt-1 definiuje 3 regiony: n n n o (-∞, -337) (-337, 0) (0, + ∞) Każdy liść drzewa zawiera model AR(1)

ART(p) o o Ograniczamy się do podzbioru modeli ART, które nazwiemy drzewami autoregresyjnymi o długości p, ozn. ART(p) W tym modelu każdy liść zawiera AR(p), zmienne rozdzielające (split variables) dla drzewa decyzyjnego są wybierane wśród poprzednich p zmiennych w szeregu czasowym

ART(p) - definiowanie o o Każdy węzeł nie będący liściem jest skojarzony z formułą boolowską, która jest funkcją p zmiennych Np. korzeń drzewa z przykładu testuje czy Z każdą krawędzią kojarzymy formułę (jej negację) z jej ojca, kiedy etykieta krawędzi ma wartość true (false) Każdy liść kojarzymy z indykatorem (indicator function) , który zwraca 1 gdy wszystkie formuły na krawędziach wzdłuż ścieżki z korzenia do tego liścia mają wartość true, 0 w p. p.

Indykator - przykład o o 1, gdy 0 w p. p.

ART(p) - definicja o Ostatecznie model ART(p) jest zadany równaniem gdzie o o L – liczba liści i regresji liniowej w liściu - parametry modelu dla

ART(p) o o Modele ART są uogólnieniami AR, gdyż ART(p) z drzewem decyzyjnym, które ma jeden węzeł jest modelem AR(p) ART(p) są mocniejsze niż AR, ponieważ pozwalają uchwycić nieliniowe zależności w szeregu czasowym Co więcej, ART(p) mogą uwzględniać zjawisko periodyczności (periodic time series) Przykład: potencjalne przewagi ART nad AR

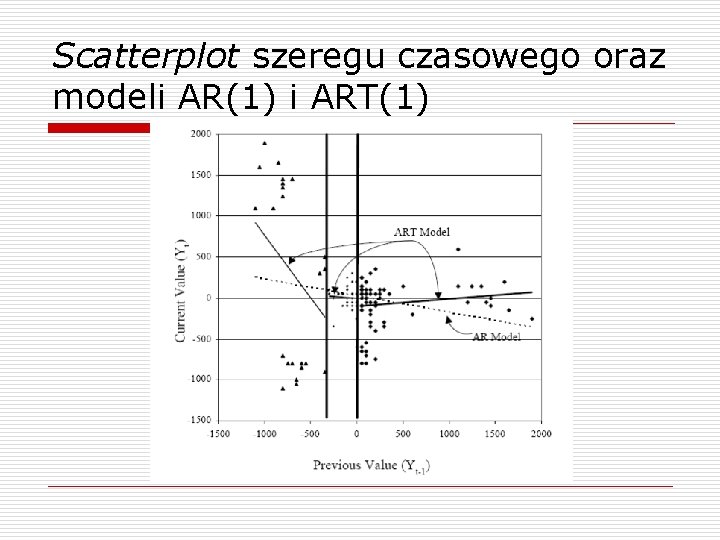
Scatterplot szeregu czasowego oraz modeli AR(1) i ART(1)

Scatterplot: wnioski o o W zależności od wartości zmiennej, stosowana może być inna formuła autoregresyjna (w przykładzie: 3 różne modele AR) Model ART tworzy lepszą aproksymację, która jest bardziej dopasowana do danych niż model AR

Inne nieliniowe modele autoregresyjne o SETAR – Self Exciting Threshold Autoregressive Models – Tong n o ASTAR – Adaptive Smooth Threshold Regressive Models – Lewis, Ray, Stevens n o Słabszy model - pojedyńcza zmienna rozdzielająca Zastosowanie MARS (multiple adaptative regression splines) do szeregów czasowych Sieci neuronowe n Skuteczne, ale kosztowne w uczeniu

Uczenie ART o Uczenie Bayesowskie n Każdy obserwowany przykład zmienia estymowane prawdopodobieństwo poprawności n Metoda „przeglądu i oceny” n Metryka oceny: Bayesian score n Koszt obliczenia metryki: , gdzie Ci – liczba przypadków, które „wpadają” do liścia li

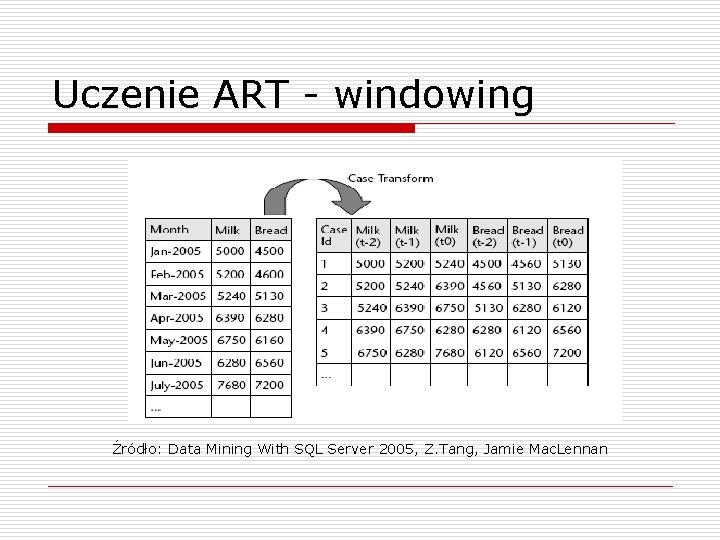
Uczenie ART - windowing o Transformacja „okienkowa” – windowing n n o o Pojedyńczy ciąg przypadków przekształcamy do zbioru wg wzoru: , dla , gdzie Tak przekształcony zbiór danych nazywamy transformacją o długości p oryginalnego szeregu czasowego Przykład: y = (1, 3, 2, 4). n n Transformacją o długości 2 jest zbiór {x 1=(1, 3), x 2=(3, 2), x 3=(2, 4)} Transformacja o długości 3 to x 1=(1, 3, 2), x 2=(3, 2, 4)

Uczenie ART - windowing Źródło: Data Mining With SQL Server 2005, Z. Tang, Jamie Mac. Lennan

Uczenie ART o o o Po uwzględnieniu transformacji, mamy prawdopodobieństwo modelu To prawdopodobieństwo jest dokładnie prawdopodobieństwem zwykłego modelu regresyjnego ze zmienną objaśnianą i zmiennymi objaśniającymi Możemy więc zastosować każdą technikę regresyjną, w szczególności drzewa decyzyjne

Uczenie ART – budowanie drzewa o 2 przypadki: n n o p jest znane – tym się zajmiemy p jest nieznane – pochodna pierwszego przypadku Znane p: n n Stosujemy algorytm greedy search i operator split-leaf(Y, n) Początkowo drzewo składa się tylko z korzenia Iteracyjnie aplikujemy split-leaf w każdym liściu dla każdej zmiennej Wybieramy ten podział, który najbardziej zwiększa metrykę (Bayesian score). Jeśli żaden podział nie zwiększa metryki, kończymy

Budowanie drzewa – p nieznane o o Stosujemy algorytm dla znanego p – trenujemy model ART(i), i wybieramy model z największą wartością metryki Bayesian score Złożoność: , gdzie L – liczba liści, T – długość szeregu

Prognozowanie z użyciem ART o o Problem: mając daną sekwencję obserwacji znaleźć rozkład przyszłych obserwacji Rozróżniamy 2 typy prognozowania: n n Jednokrokowe (one-step forecasting) Wielokrokowe (multi-step forecasting)

Prognozowanie jednokrokowe o o Mamy dane , interesuje nas wartość Przybliżamy ją rozkładem normalnym Jako wartość przyjmujemy najbardziej prawdopodobną wartość (maximum a posteriori value): Prognozowanie wielokrokowe jest trudniejsze n Metody Monte Carlo

Porównanie efektywności o o o o http: //www. forecasters. org/data/m 3 comp. htm Długość szeregów: od 23 do 126 Dane: produkcja przemysłowa, dane makro- i mikroekonomiczne, finansowe Dla każdego zbioru danych utworzono 9 zbiorów z użyciem transformacji o długości p, p=0, 1, . . 8 Dane wycentrowane i wystandaryzowane Dodatkowo podział na dane treningowe i testowe Metryka: sequential predictive score

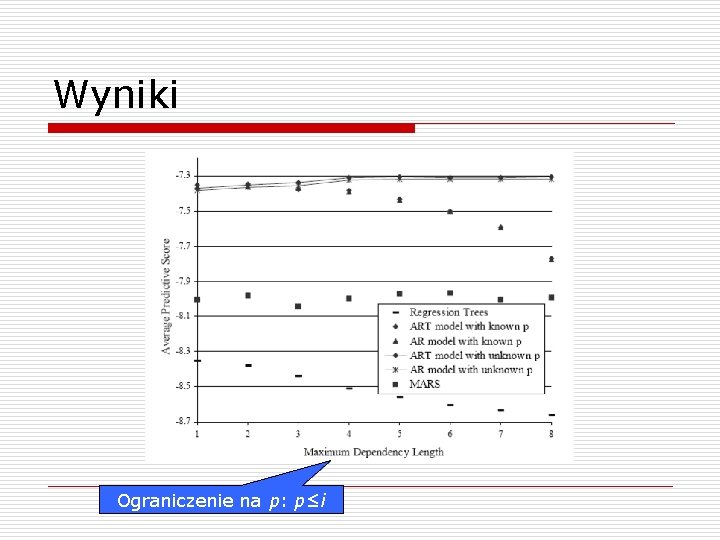
Wyniki Ograniczenie na p: p≤i

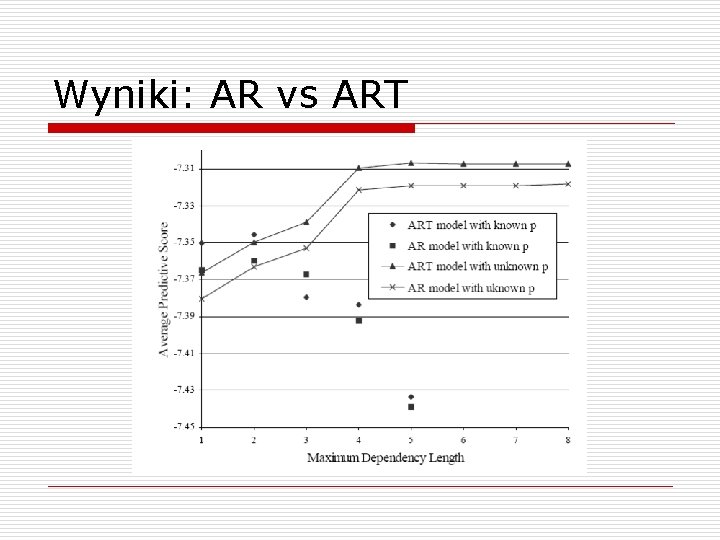
Wyniki: AR vs ART

Wyniki o o Tylko w 5% przypadków wynikowe drzewo ART miało jakiś podział (split) – krótkie szeregi testowe Dodatnia korelacja między długością szeregu a ilością podziałów w drzewie Model ART jest lepszy od „zwykłej” autoregresji Różnica jest tym większa, czym dłuższy badany szereg czasowy

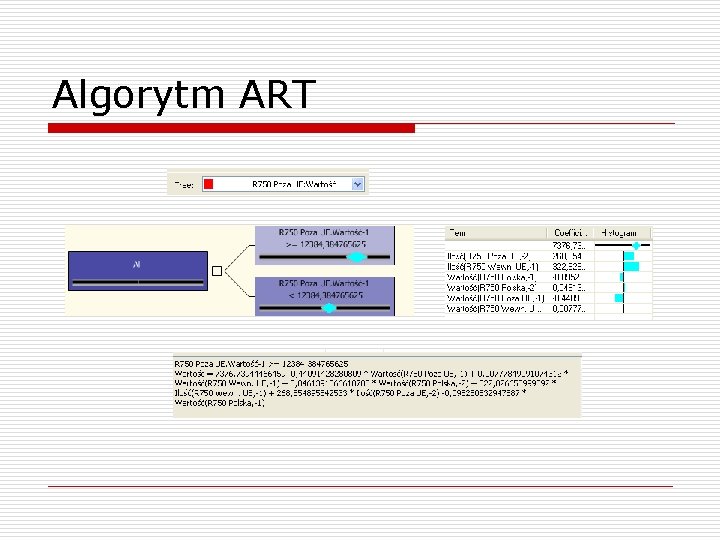
Zastosowanie w praktyce o o Algorytm ART został zaimplementowany w Microsoft SQL Server 2005 jako podstawowe narzędzie do analizy szeregów czasowych Nazwa handlowa: Microsoft Time Series

Algorytm ART

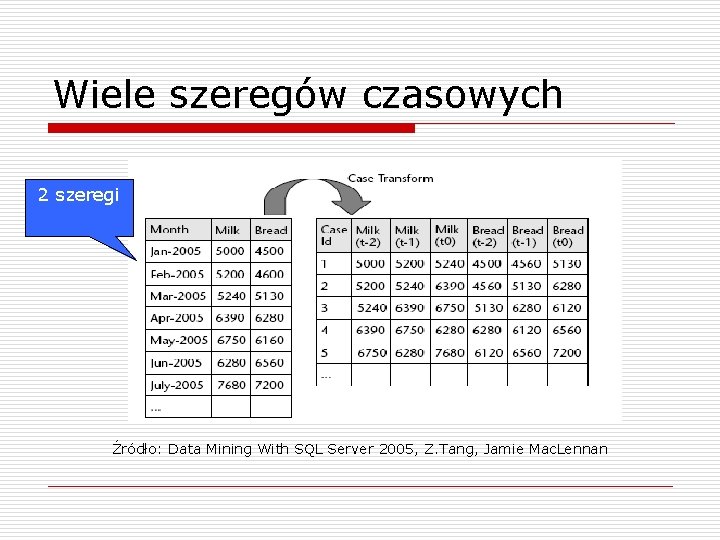
Wiele szeregów czasowych o o Szeregi czasowe często wykazują mocną zależność między sobą n cena benzyny/sprzedaż nowych samochodów n stopy procentowe/koszty kredytów konsumpcyjnych Microsoft Time Series potrafi rozpoznać i wykorzystać takie korelacje

Wiele szeregów czasowych 2 szeregi Źródło: Data Mining With SQL Server 2005, Z. Tang, Jamie Mac. Lennan

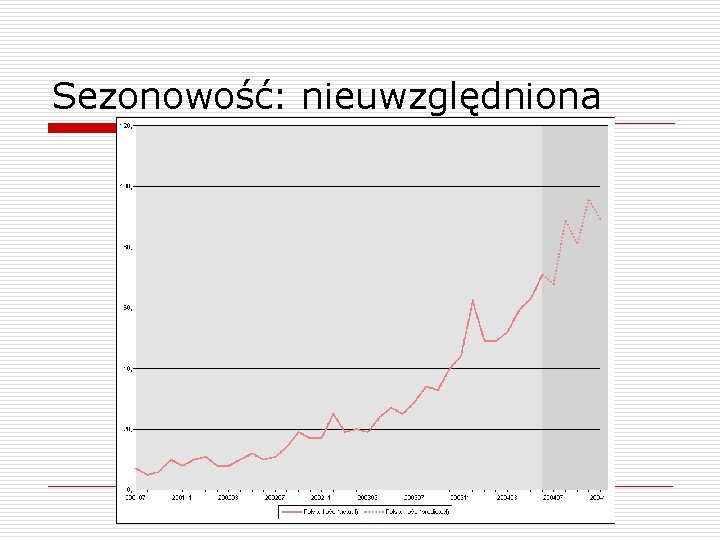
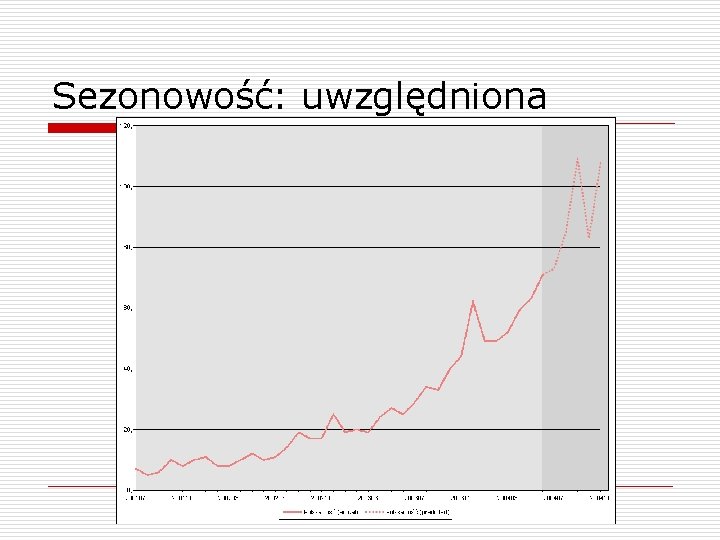
Sezonowość o o o Wiele szeregów czasowych wykazuje wyraźne wahania sezonowe Największe obroty w grudniu, „martwy sezon” latem Microsoft Time Series posiada wbudowaną obsługę sezonowości: n możliwość jawnego podania – np. Periodicity_Hint=12 n automatyczne wykrywanie sezonowości na podstawie FFT (szybkiej transformacji Fouriera) Dodawane są dodatkowe zmienne objaśniające Można też „odsezonowić” dane przed zastosowaniem algorytmu

Sezonowość: nieuwzględniona

Sezonowość: uwzględniona

Koniec Dziękuję za uwagę!