Modelbased species identification using DNA barcodes Bogdan Paaniuc

Model-based species identification using DNA barcodes Bogdan Paşaniuc CSE Department, University of Connecticut Joint work with Ion Măndoiu and Sotirios Kentros

Outline n Existing approaches to species identification n Proposed statistical model based methods n Experimental Results n Ongoing Work and Conclusions

Background on DNA barcoding n Recently proposed tool for species identification n Use short DNA region as “fingerprint” for the species n Region of choice: cytochrome c oxidase subunit 1 mitochondrial gene ("COI", 648 base pairs long). n Key assumption: inter-species variability higher than intra-species variability

Species identification problem n Given: ¡ ¡ n Database DB containing barcodes from known species New barcode x Find: ¡ a high confidence assignment to a species in the DB Ø n UNKNOWN, if confidence not high enough Use additional evidence/methods to resolve UNKNOWN assignments and possible discovery of new species

Existing approaches and limitations n Neighbor Joining tree for new + known barcodes [Meyers&Paulay 05] ¡ ¡ n Likelihood ratio test for species membership using MCMC [Matz&Nielsen 06] ¡ n One barcode per species Runtime does not scale well with #species (quadratic or worse) Impractical runtime even for moderate #species Distance-based [BOLD-IDS, Tax. I(Steinke et al. 05)] ¡ Unclear statistical significance

BOLD n BOLD: The Barcode of Life Data Systems [Ratnasingham&Hebert 07] ¡ http: //www. barcodinglife. org ¡ Currently: 28, 129 species, 251, 429 barcodes n Identification System: BOLD-IDS ¡ Distance-based (NJ tree for visualization) ¡ Employs a threshold (less than 1% divergence) to get a tight match to a barcode in the DB

BOLD-IDS n [Ekrem et al. 07]: “…identifications by the BOLD facility must be cautiously evaluated as the system at present may return high probabilities of placements that obviously are erroneous”

Outline n Existing approaches to species identification n Proposed statistical model based methods n Experimental Results n Ongoing Work and Conclusions

Bayesian approach to species identification n Assign barcode x=x x x …x to species SP that maximizes P(SP |x) over all species SP 1 2 3 i n i i P(SP |x) computed using Bayes’ theorem: P(SP|x) = P(x|SP)*P(SP)/P(x) i ¡ ¡ ¡ n n Uniform prior P(SP) P(x) constant for fixed x Need model for P(x|SP) We explored three scalable models: position weight matrices, Markov chains, hidden Markov models ¡ Similar to models used successfully in other sequence analysis problems such as DNA motif finding and protein families

Positional weight matrix (PWM) n Assumption: independence of loci ¡ n P(x|SP) = P(x 1|SP)*P(x 2|SP)*…*P(xn|SP) For each locus, P(xi|SP) is estimated as the probability of seeing each nucleotide at that locus in DB sequences from species SP

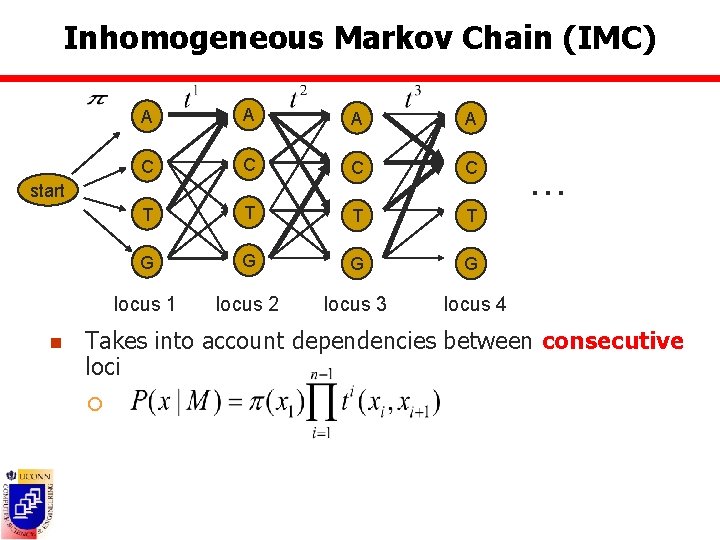
Inhomogeneous Markov Chain (IMC) A A C C T T G G locus 1 locus 2 locus 3 locus 4 start n … Takes into account dependencies between consecutive loci ¡

Hidden Markov Model (HMM) n Same structure as the IMC ¡ Each state emits the associated DNA base with high probability; but can also emit the other bases with probability equal to mutation rate n Barcode x generated along path p with probability equal to product of emission & transitions along p n P(x|HMM) = sum of probabilities over all paths ¡ Efficiently computed by forward algorithm

Accuracy on BOLD dataset n n 10% 20% 30% 40% 50% PWM 90. 08% 90. 01% 90. 02% 89. 68% 89. 69% IMC 99. 97% 99. 93% 99. 90% 99. 91% 99. 89% HMM 99. 57% 99. 66% 99. 70% 99. 76% 37 species with at least 100 barcodes from BOLD ¡ 10 -50% barcodes removed and used for test IMC yields better accuracy in all cases

Score normalization n n DB barcodes have non uniform lengths and cover different regions of the COI gene ¡ Membership probabilities not always comparable Normalization scheme: ¡ Species models constructed only over positions covered in DB ¡ Scores normalized using background IMC constructed from all sequences in DB

Computing the confidence of assignment n n n x assigned to species SP with score s p-value: probability that a barcode generated under background model Ḿ has a score s’ s Methods for p-value estimation: ¡ Random sampling Ø Generate random sequences and count how many exceed the score ¡ Exact computation (for PWMs): Ø Dynamic programming [Rahmann 03] Ø Branch and bound [Zhang et. Al 07] Ø Shiffted FFTs [Nagarajan et al. 05]

Exact computation for PWMs [Rahmann 03] n Computes the entire distribution n Scores rounded by a granularity factor n Score is a sum of n independent variables (score contribution of each position) ¡ Probability of a rand. seq. of length i having a score of computed from the contribution of first i-1 positions and current position

Exact computation for IMCs n Define as the prob. of a random seq of length i having score and last letter n Basic recurrence:

IMC exact p-value computation n Initially n The probability of a random barcode having score n Runtime , where R is the difference between max and min score for any i.

Outline n Existing approaches to species identification n Proposed statistical model based methods n Experimental Results n Ongoing Work and Conclusions

Experimental setup (1) n Compared methods ¡ IMC Ø Species with highest score Ø If score < species specific threshold UNKNOWN ¡ Distance-based (BOLD-IDS like) Ø Species containing barcode showing less divergence Ø If divergence > threshold (default 1%) UNKNOWN n Basic questions ¡ What is the effect of training set size (#barcodes per species) on accuracy? ¡ What is the effect of the #species on accuracy?

Experimental setup (2) n Two scenarios: ¡ Complete DB: all new barcodes belong to species in DB ¡ Incomplete DB: some new barcodes belong to species not in DB

Accuracy measures n True positive rate = TP/(TP+FP) ¡ Barcodes belonging to species present in the DB = #barcodes assigned to correct species Ø FP = #barcodes assigned to incorrect species Ø TP ¡ Barcodes belonging to species not present in DB = #barcodes assigned to unknowns Ø FP = #barcodes assigned to species in the DB Ø TP

Effect of #barcodes/species n Datasets containing all BOLD species with at least 5/25 barcodes ¡ BOLD 5: 1508 sp, 28600 barcodes ¡ BOLD 25: 270 sp, 17197 barcodes n DB composed of randomly picked 5 -20 barcodes from all species in BOLD 25 n Test barcodes ¡ Complete database scenario Ø ¡ All remaining barcodes from BOLD 25 Incomplete database scenario Ø All barcodes from BOLD 5 not in DB

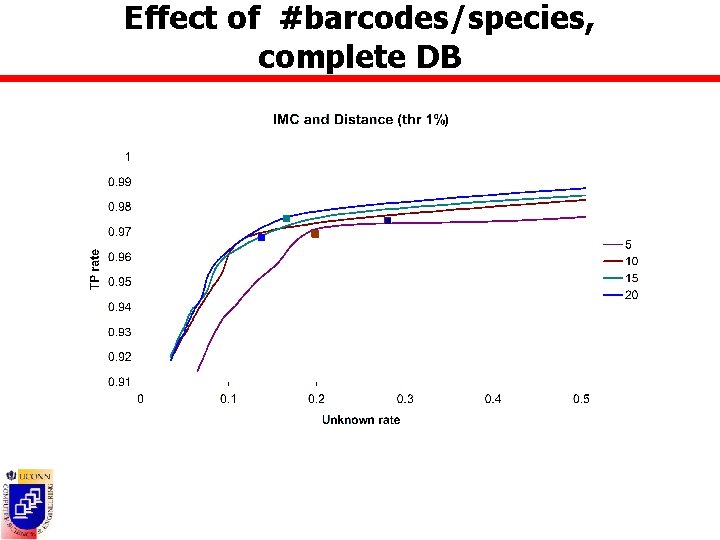
Effect of #barcodes/species, complete DB

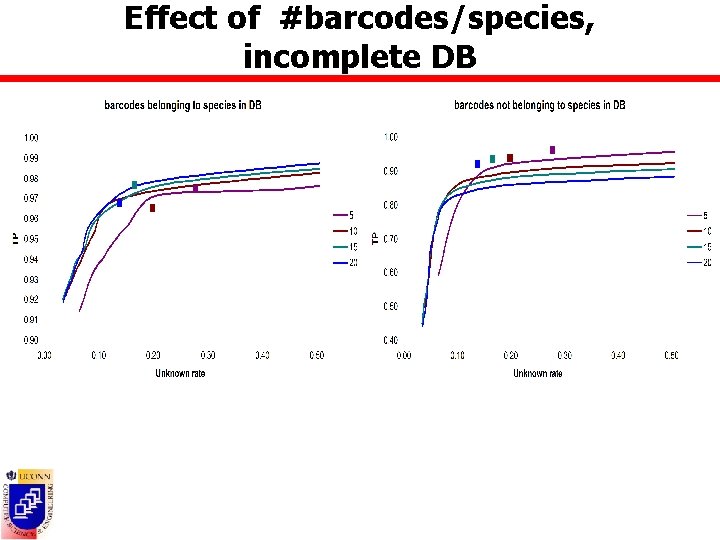
Effect of #barcodes/species, incomplete DB

Effect of #species n Datasets containing all BOLD species with at least 5/10 barcodes ¡ ¡ n DB composed of randomly picked 100 to 690 species from BOLD 10 ¡ n BOLD 5: 1508 sp, 28600 barcodes BOLD 10: 690 sp, 23558 barcodes 10 barcodes per species Test barcodes ¡ Complete database scenario Ø ¡ All remaining barcodes from picked species Incomplete database scenario Ø All barcodes from BOLD 5 not in DB

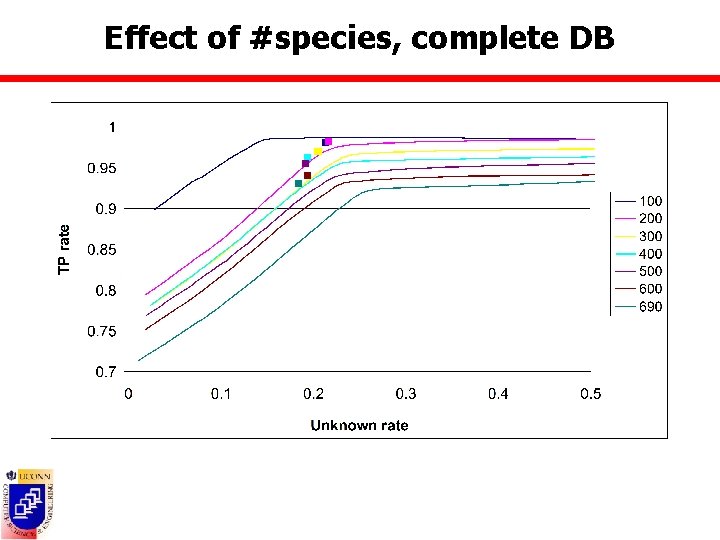
Effect of #species, complete DB

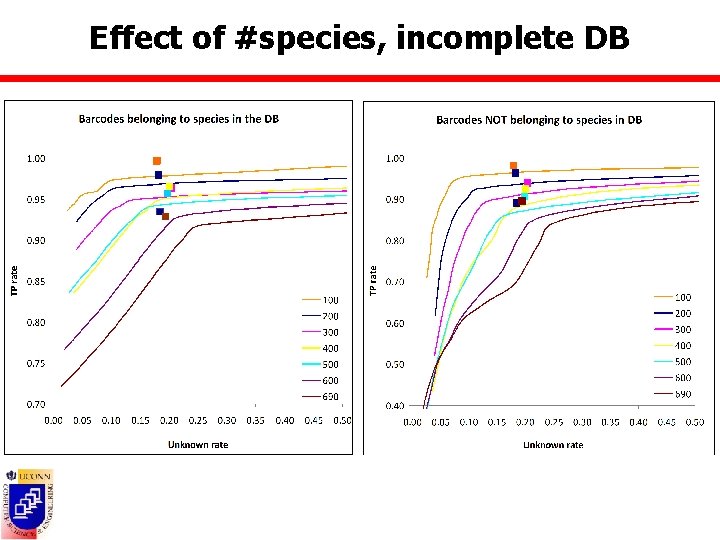
Effect of #species, incomplete DB

Outline n Existing approaches to species identification n Proposed statistical model based methods n Experimental Results n Ongoing Work and Conclusions

Conclusions & Ongoing work n IMC provides a scalable method for species identification ¡ ¡ n High accuracy, with useful tradeoff between TP rate and unknown rate Efficiently computable p-values Comprehensive comparison of identification algorithms to be submitted to 2 nd International Barcode Conference ¡ Broad coverage of methods Ø ¡ Assessment of further effects besides #species and #barcodes/species Ø Ø ¡ tree-based, distance-based, character-based, model-based Barcode length Barcode quality Number of regions Runtime scalability (up to millions of species) Diverse datasets (BOLD, cowries, flu viruses, simulated data, etc. )