MODELADO Y SIMULACIN DE SISTEMAS Modelo y simulacin

MODELADO Y SIMULACIÓN DE SISTEMAS

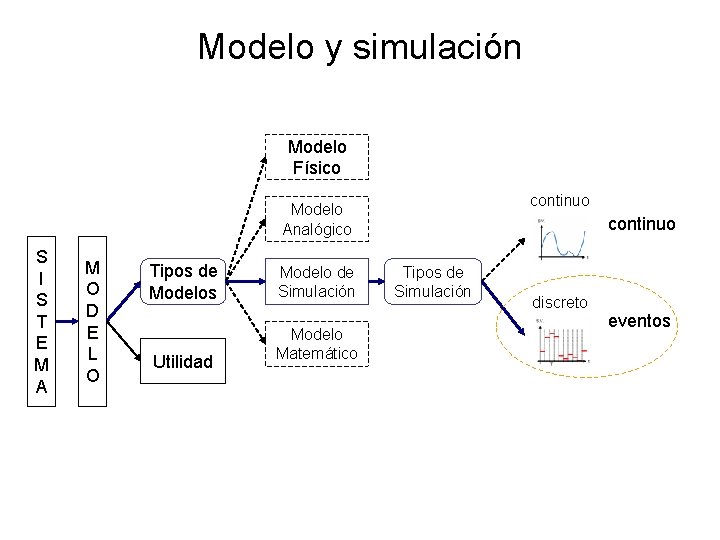
Modelo y simulación Modelo Físico continuo Modelo Analógico S I S T E M A M O D E L O Tipos de Modelos Utilidad Modelo de Simulación Modelo Matemático continuo Tipos de Simulación discreto eventos

SISTEMAS

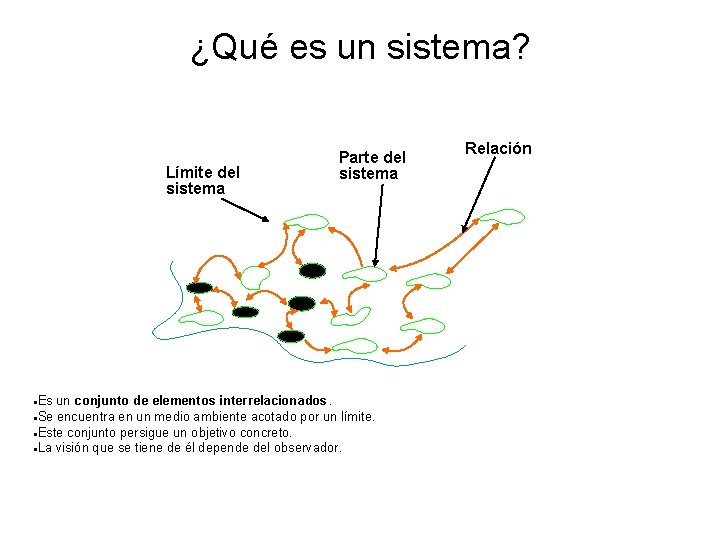
¿Qué es un sistema? Límite del sistema Parte del sistema Es un conjunto de elementos interrelacionados. Se encuentra en un medio ambiente acotado por un límite. Este conjunto persigue un objetivo concreto. La visión que se tiene de él depende del observador. Relación

Ejercicio 1 • ¿Todos los sistemas son iguales? • ¿De qué depende su definición?

Definición de los sistemas Estructural • Se define el sistema identificando y describiendo cada uno de sus componentes y sus interrelaciones. • Se considera que tras hacer esto se puede conocer el sistema. De comportamiento (Funcional) • Se define el sistema considerándolo como una caja negra y describiendo sus respuestas ante los posibles valores en las entradas. • Se conoce el sistema definiendo su dinámica.

Ejercicio 2 Diga a qué tipo de definición de sistemas corresponde cada uno de los siguientes: 1. Diagrama de un circuito electrónico. 2. Plano de una casa. 3. Diagrama de procesos de una organización. 4. Organigrama. 5. Modelo de control de una planta. 6. Modelo epidemiológico de una enfermedad.

Propiedades de los sistemas Sinergia. • Con los componentes y su interrelación se consigue más que lo que en principio resultaría de la simple suma de los componentes. Entropía • Refleja el grado de desorden del sistema. Se puede reducir la entropía ingresando información al sistema. Equilibrio homeostático. • Equilibrio dinámico que mantiene los valores dentro de un rango establecido.

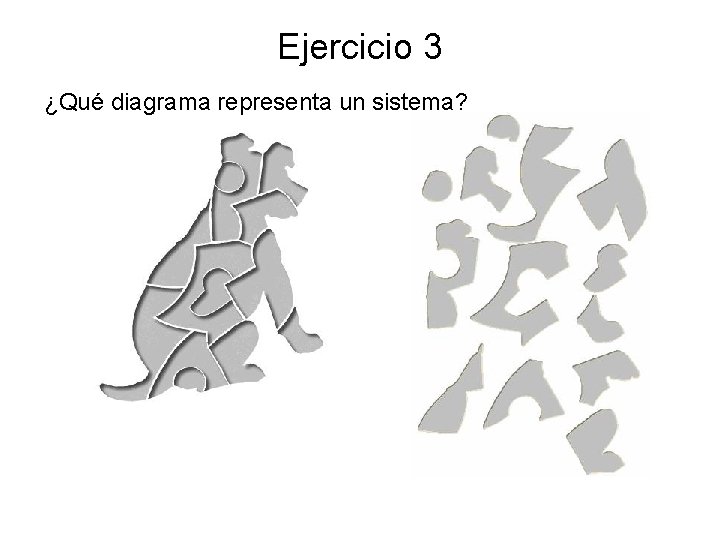
Ejercicio 3 ¿Qué diagrama representa un sistema?

Ejercicio 4 ¿Cómo colocar 8 reinas en un tablero de ajedrez de tal manera que no se amenacen entre ellas?

¿Dónde están los sistemas? ¿Sistema?

¿Dónde están los sistemas? Los sistemas se definen construcciones mentales. Su definición se corresponde con la representación o modelo mental de los objetos del mundo real. Cada sistema depende del punto de vista del observador (modelador). Diferentes Personas Diferentes Visiones Diferentes Sistemas

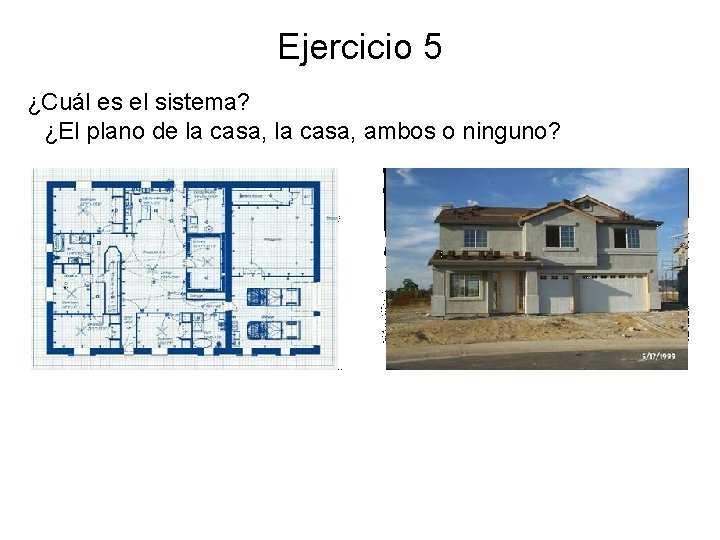
Ejercicio 5 ¿Cuál es el sistema? ¿El plano de la casa, ambos o ninguno?

MODELOS

Modelo • Es una abstracción de la realidad. • Es una representación de la realidad que ayuda a entender su composición y/o funcionamiento. • Es una construcción intelectual y descriptiva de una entidad en la que un observador tiene interés. • Se construye para transmitirse. • Se emplean supuestos simples para restringirse a lo que se considera relevante y evitar lo que no. Un modelo es un sistema desarrollado para entender la realidad y, en consecuencia, para modificarla. No es posible modificar la realidad, en cierta dirección, si no se dispone de un modelo que la interprete.

Ejercicio 8 • Modelar la siguiente realidad • ¿Qué aspecto es importante? • ¿De qué depende la importancia?

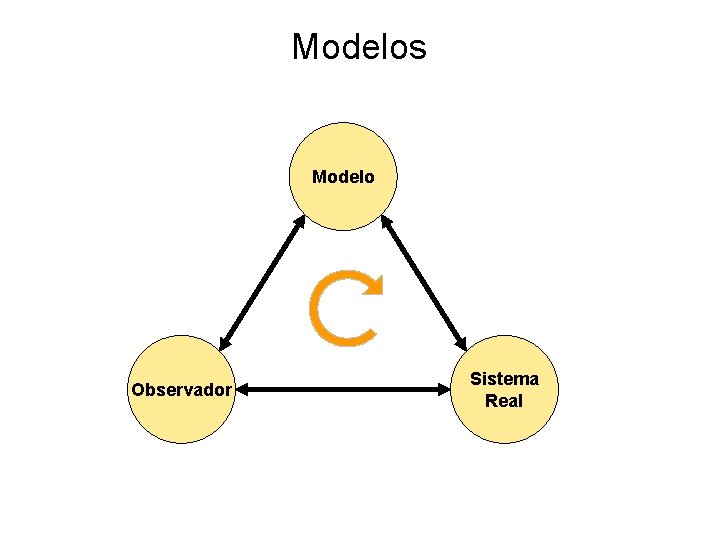
Modelos Modelo Observador Sistema Real

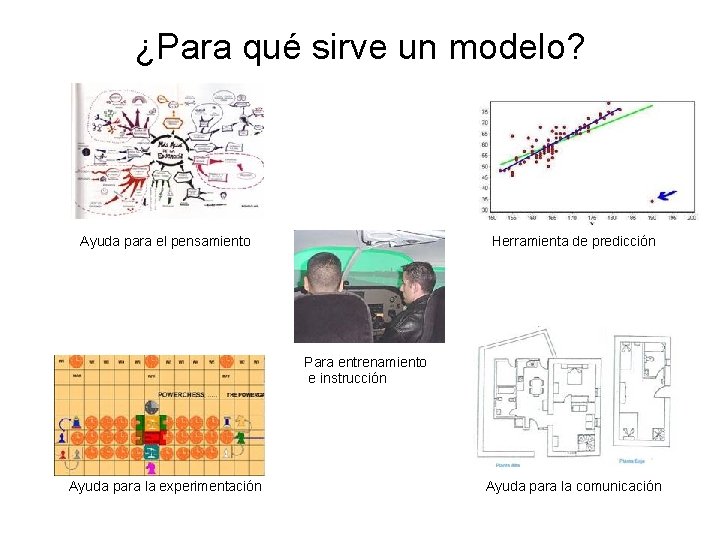
¿Para qué sirve un modelo? Ayuda para el pensamiento Herramienta de predicción Para entrenamiento e instrucción Ayuda para la experimentación Ayuda para la comunicación

Modelos Mentales y Formales • Modelos Mentales. Depende de nuestro punto de vista, suele ser incompletos y no tener un enunciado preciso, no son fácilmente transmisibles. Ideas, conceptualizaciones • Modelos Formales. Están basados en reglas, son transmisibles. Planos, diagramas, maquetas, ecuaciones, descripciones en HDL,

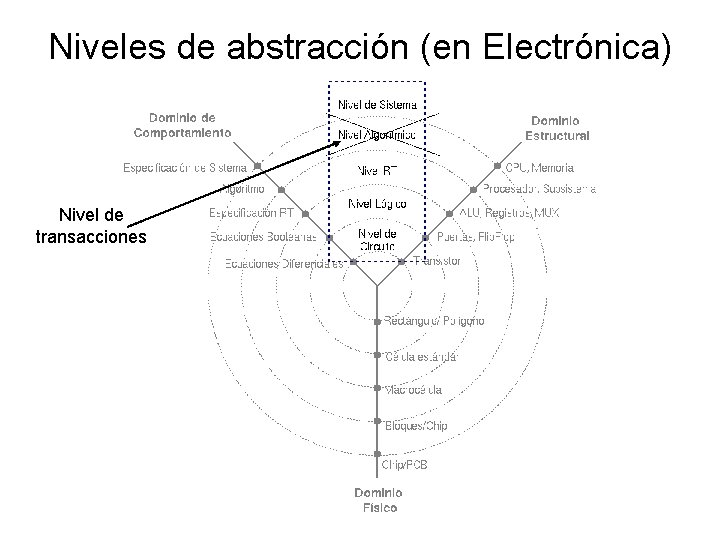
Niveles de abstracción (en Electrónica) Nivel de transacciones

Ejercicio 6 ¿A qué categoría (mental o formal) pertenecen los siguientes modelos? 1. Opinión sobre el nuevo gabinete. 2. Opinión sobre el nuevo gabinete escrito en El Comercio. 3. Dibujo hecho a mano acerca de la nueva casa. 4. Plano de la nueva casa. 5. Modelo de clases o objetos del área de ventas. 6. Orden en que llegan los elementos de entrada a una máquina. 7. Distribución de probabilidad del orden en que llegan los elementos de entrada a una máquina. 8. Orden que sigue un documento para ser aprobado. 9. Diagrama de flujo de un algoritmo para aprobar documentos.

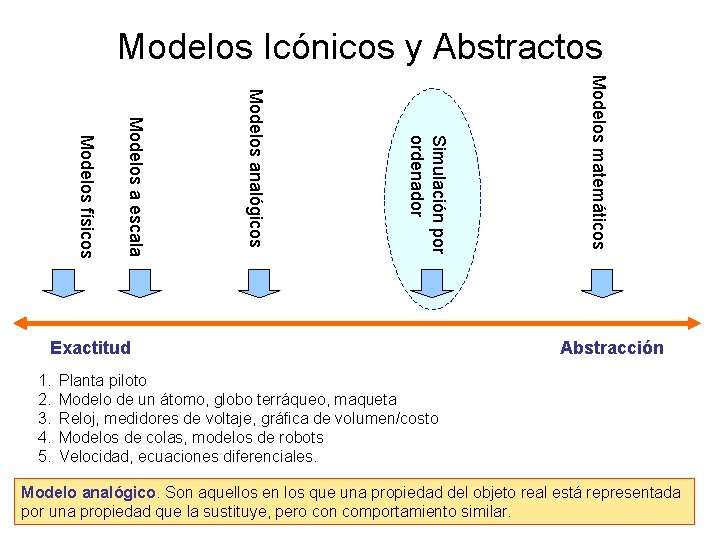
Modelos Icónicos y Abstractos 1. 2. 3. 4. 5. Modelos matemáticos Simulación por ordenador Modelos analógicos Modelos a escala Modelos físicos Exactitud Abstracción Planta piloto Modelo de un átomo, globo terráqueo, maqueta Reloj, medidores de voltaje, gráfica de volumen/costo Modelos de colas, modelos de robots Velocidad, ecuaciones diferenciales. Modelo analógico. Son aquellos en los que una propiedad del objeto real está representada por una propiedad que la sustituye, pero con comportamiento similar.

Ejercicio 7 Relaciona las siguientes dos listas. Identificar qué modelo(s) se usa(n) para representar los siguientes aspectos de la realidad. Indicar el tipo de modelo realidad 1. 2. 3. 4. 5. 6. 7. 8. 9. Oficina Bancaria Temperatura Edificio País Empresa Software Epidemia Reacción Nuclear Energía 1. 2. 3. 4. 5. 6. 7. 8. 9. Termómetro Mapa Plano Organigrama Diagrama Causal Cola M/M/1 Diagrama de flujo Modelo Matemático E = mc 2

TIPOS DE MODELOS

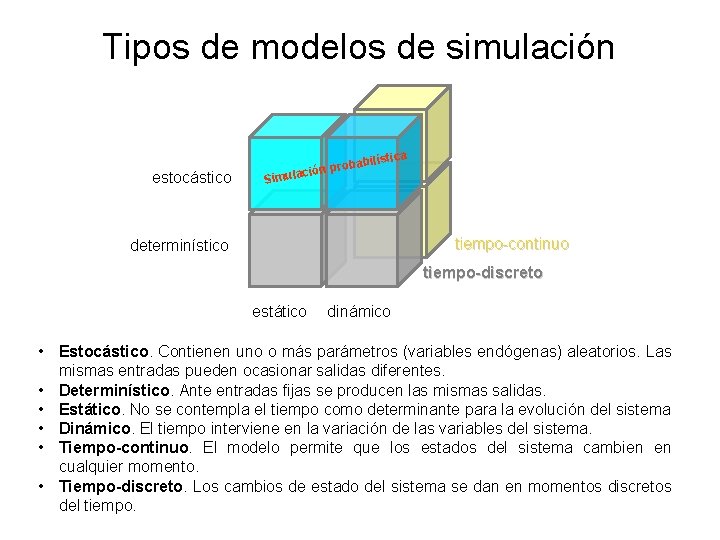
Tipos de modelos de simulación estocástico lística babi ión pro c Simula tiempo-continuo determinístico tiempo-discreto estático dinámico • Estocástico. Contienen uno o más parámetros (variables endógenas) aleatorios. Las mismas entradas pueden ocasionar salidas diferentes. • Determinístico. Ante entradas fijas se producen las mismas salidas. • Estático. No se contempla el tiempo como determinante para la evolución del sistema • Dinámico. El tiempo interviene en la variación de las variables del sistema. • Tiempo-continuo. El modelo permite que los estados del sistema cambien en cualquier momento. • Tiempo-discreto. Los cambios de estado del sistema se dan en momentos discretos del tiempo.

Estocástico - Determinístico Estocástico (*) Si el estado de la variable en el siguiente instante de tiempo no se puede determinar con los datos del momento actual xi yj = fm(xi, lk) (Existen variables internas –como lk– aleatorias) yj Método analítico: usa probabilidades para determinar la curva de distribución de frecuencias Determinístico Si el estado de la variable en el siguiente instante de tiempo se puede determinar con los datos del estado actual xi yj = fm(xi) yj Método numérico: algún método de resolución analítica

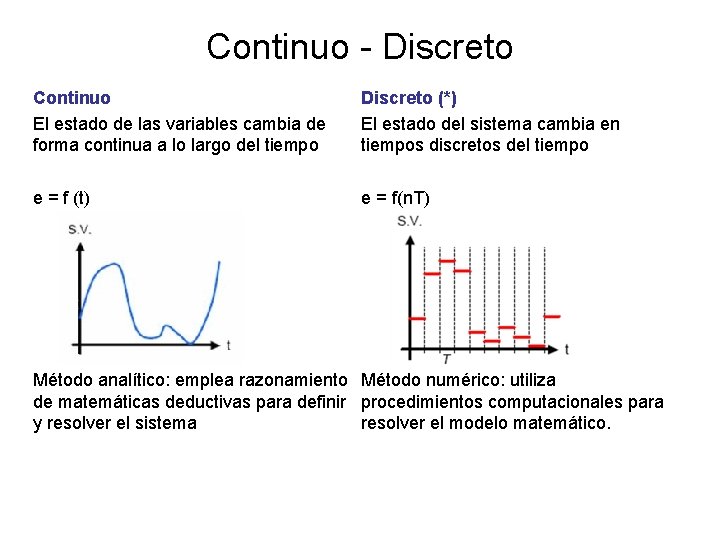
Continuo - Discreto Continuo El estado de las variables cambia de forma continua a lo largo del tiempo Discreto (*) El estado del sistema cambia en tiempos discretos del tiempo e = f (t) e = f(n. T) Método analítico: emplea razonamiento Método numérico: utiliza de matemáticas deductivas para definir procedimientos computacionales para y resolver el sistema resolver el modelo matemático.

Estático - Dinámico Estático Entre las variables no se encuentra la variable tiempo. Dinámico (*) Si el estado de las variables puede cambiar mientras se realiza algún cálculo f [ n. T ] ≠ f [ n(T+1) ] Método analítico: algún método de resolución analítica. Método numérico: usa procedimientos computacionales para resolver el modelo matemático.

SIMULACION

Simulación • Es la construcción de modelos informáticos que describen la parte que se considera esencial del comportamiento de un sistema de interés, así como diseñar y realizar experimentos con este modelo y extraer conclusiones de sus resultados para apoyar la toma de decisiones. • Se usa como un paradigma para analizar sistemas complejos. La idea es obtener una representación simplificada de algún aspecto de interés de la realidad. • Permite experimentar con sistemas (reales o propuestos) en casos en los que de otra manera esto no sería práctico, o bien demasiado costoso o incluso imposible.

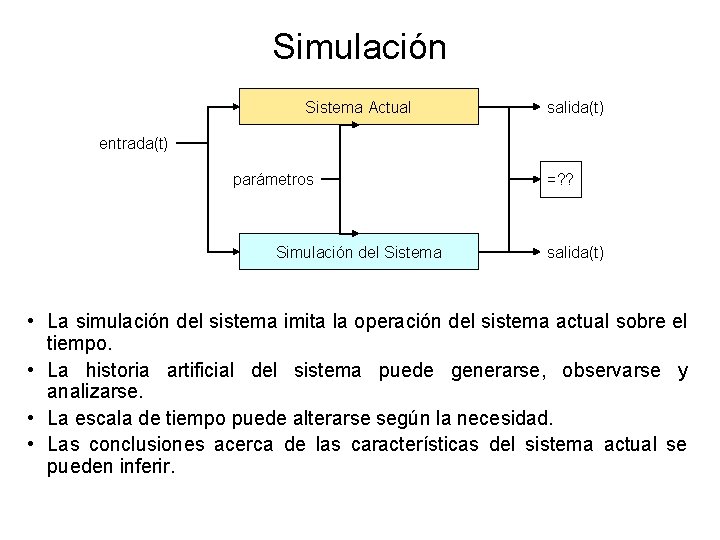
Simulación Sistema Actual salida(t) entrada(t) parámetros Simulación del Sistema =? ? salida(t) • La simulación del sistema imita la operación del sistema actual sobre el tiempo. • La historia artificial del sistema puede generarse, observarse y analizarse. • La escala de tiempo puede alterarse según la necesidad. • Las conclusiones acerca de las características del sistema actual se pueden inferir.

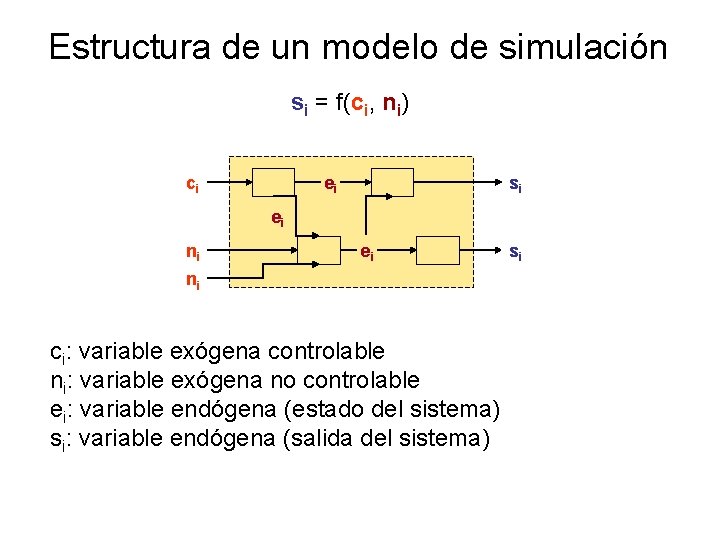
Estructura de un modelo de simulación si = f(ci, ni) ei ci si ei ni ci: variable exógena controlable ni: variable exógena no controlable ei: variable endógena (estado del sistema) si: variable endógena (salida del sistema) si

Simulación probabilística* • En ocasiones se necesitan variables aleatorias en procesos de simulación: – Algoritmos de placement & routing, de mapping. . . • Entre otras técnicas, en Electrónica las más empleadas son: – Simulación de Montecarlo – Simulated annealing – Algoritmos genéticos

Método de Montecarlo • Es un método muy general • Emplea secuencias de números aleatorios como valores de variables – – – Generador de números aleatorios Función de distribución de probabilidad Regla de muestreo Estimación de error Técnicas de reducción de varianza • Produce soluciones aproximadas • Se puede aplicar tanto en problemas contenido de naturaleza probabilística como en otros que no lo tiene

Simulated annealing • Imita el proceso de solidificación de un metal previamente fundido – La estructura queda tras el enfriamiento del metal es regular • En este enfriado el nuevo punto de la estructura que se establece debe resultar mejor que el de partida teniendo en cuenta una función de coste. • Este nuevo punto se sugiere en una variación en cualquier dirección teniendo en cuenta una determinada variación de energía al ir descendiendo la temperatura – Con temperaturas menores, la probabilidad de elegir un movimiento peor disminuye

Algoritmos genéticos • Se imita el proceso de evolución de las especies • Los nuevos individuos resultan de la evolución de los individuos de partida, pero. . . – Pueden producirse cambios por mutación (aleatorio) – Pueden producirse cambios por motivos de reproducción (adquiriendo determinadas características de los padres ) • Se evoluciona hacia miembros con mejores características • La población inicial es completamente aleatoria

PERTINENCIA

¿Cuando es apropiado simular? • No existe una completa formulación matemática del problema. • Cuando el sistema aún no existe. • Es necesario desarrollar experimentos, pero su ejecución en la realidad es difícil o imposible • Se tiene interés en establecer un periodo de observación del experimento distinto del que se podría establecer en la realidad. • No se puede interrumpir la operación del sistema actual.

¿Cuándo no es aconsejable simular? • El desarrollo del modelo de simulación requiere mucho tiempo. • El desarrollo del modelo es costoso comparado con sus beneficios. • La simulación es imprecisa y no se puede medir su imprecisión. – El análisis de sensibilidad puede ayudar en estos casos.

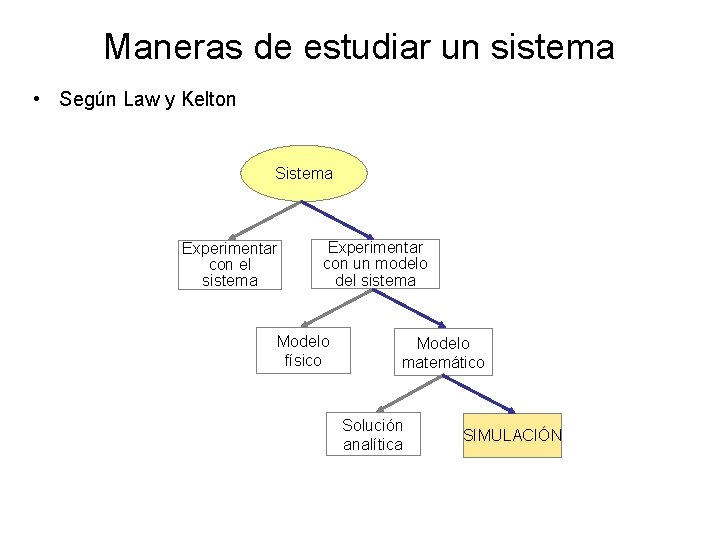
Maneras de estudiar un sistema • Según Law y Kelton Sistema Experimentar con el sistema Experimentar con un modelo del sistema Modelo físico Modelo matemático Solución analítica SIMULACIÓN

Ejercicio 8 Sistema real: Sección de caja de un supermercado. Identificar: • Elementos o entidades. • Actividades por cada entidad. • Variables exógenas: – Controlables. – No controlables. • Variables endógenas: – De estado – De salida

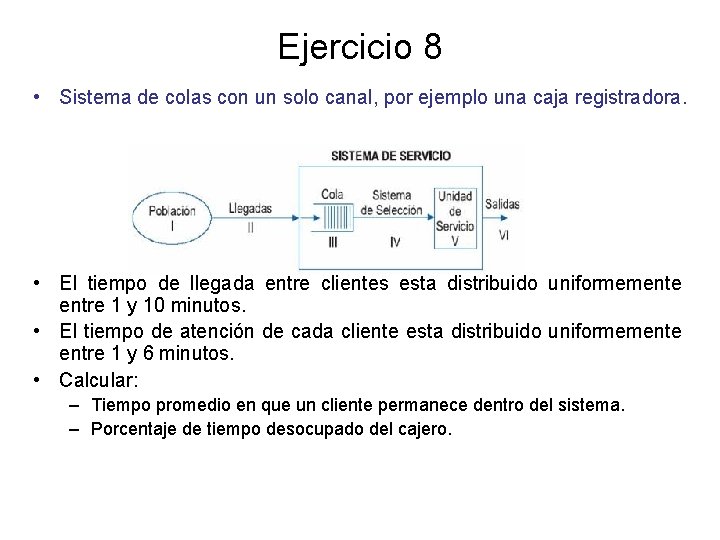
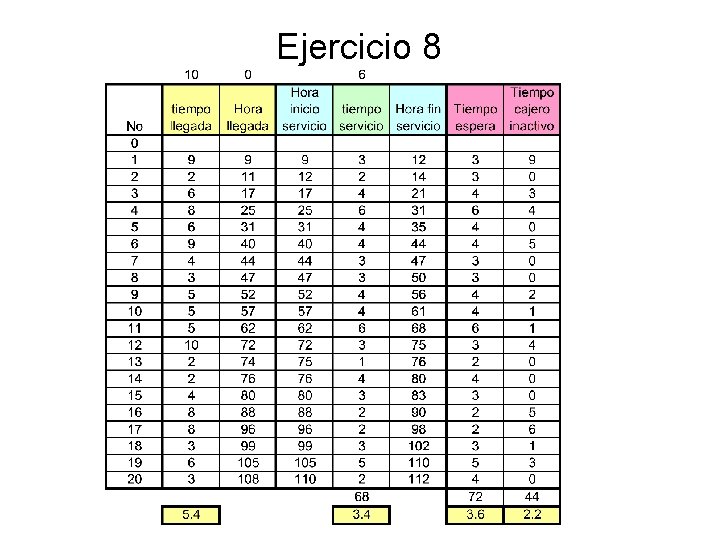
Ejercicio 8 • Sistema de colas con un solo canal, por ejemplo una caja registradora. • El tiempo de llegada entre clientes esta distribuido uniformemente entre 1 y 10 minutos. • El tiempo de atención de cada cliente esta distribuido uniformemente entre 1 y 6 minutos. • Calcular: – Tiempo promedio en que un cliente permanece dentro del sistema. – Porcentaje de tiempo desocupado del cajero.

Ejercicio 8

Conclusiones • Los modelos se construyen para entender la realidad. • Los modelos de simulación hacen uso intensivo del computador • El tipo de comportamiento de las variables determinan el comportamiento del sistema.

Bibliografía Simulación. Métodos y Aplicación. D. Ríos, S. Ríos y J. Martín. 2000. Simulación. Sheldom M. Ross. 1999. 2 da. Edición. Simulación de Sistemas Discretos. J. Barceló. 1996