Model Uncertainty and Robust Stochastic Modeling Henry Lam

Model Uncertainty and Robust Stochastic Modeling Henry Lam Department of Industrial & Operations Engineering University of Michigan

Overview Motivation: All models are wrong… Model risk / model error/ input uncertainty arises when performance analysis is based on misspecified / uncertain input model assumptions Goal: Performance analysis that is robust against model error Scope: • Input model: stochastic • Uncertainty: nonparametric

Basic Question •

Question 2: Uncertain Dependency •

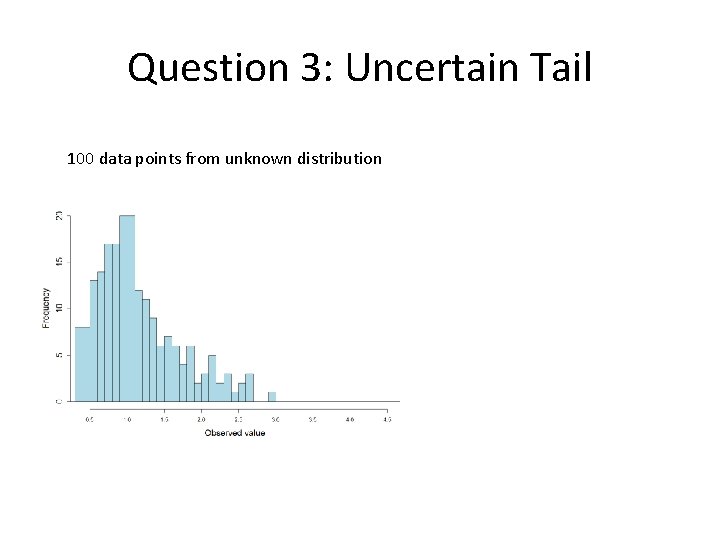
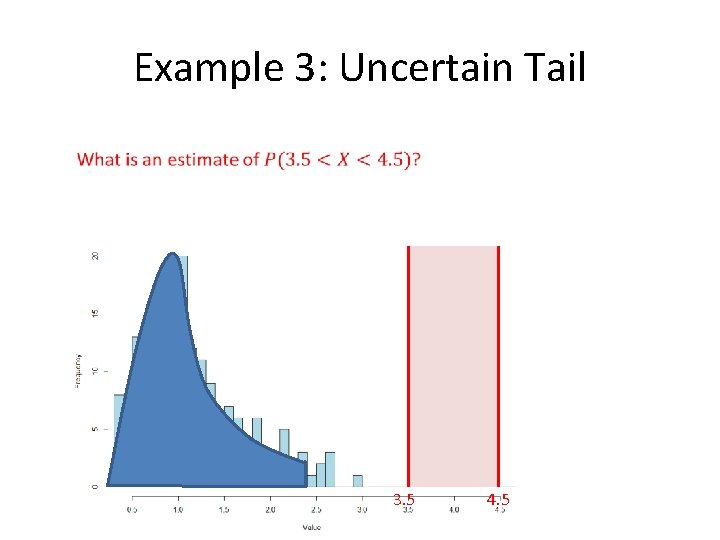
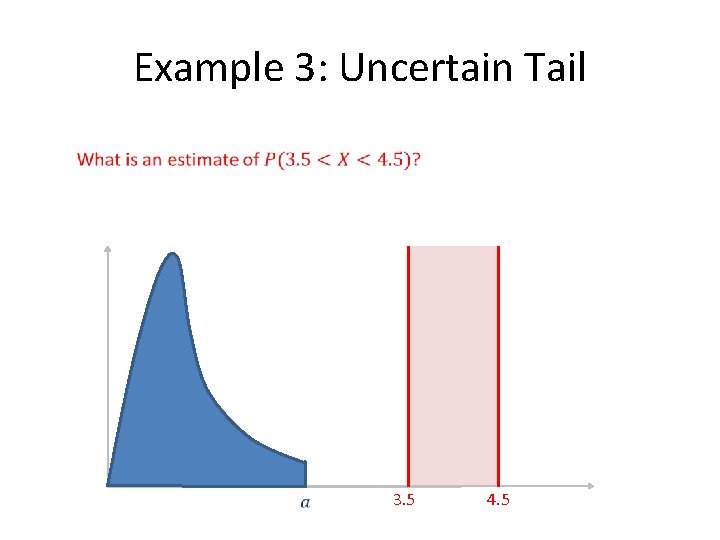
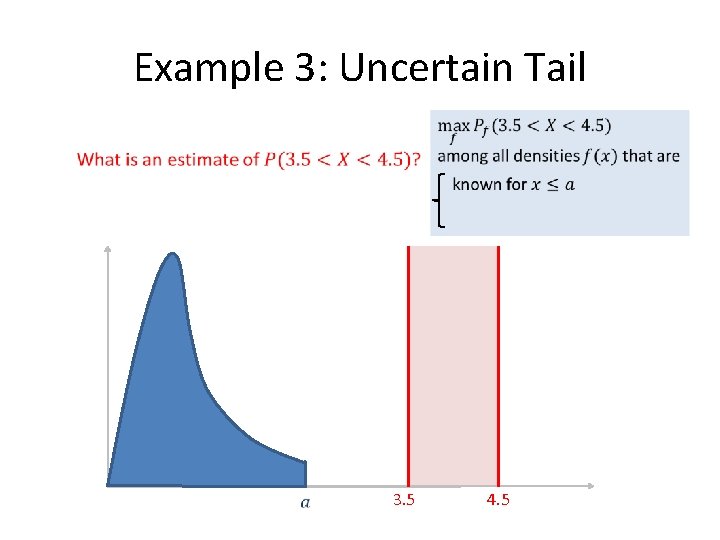
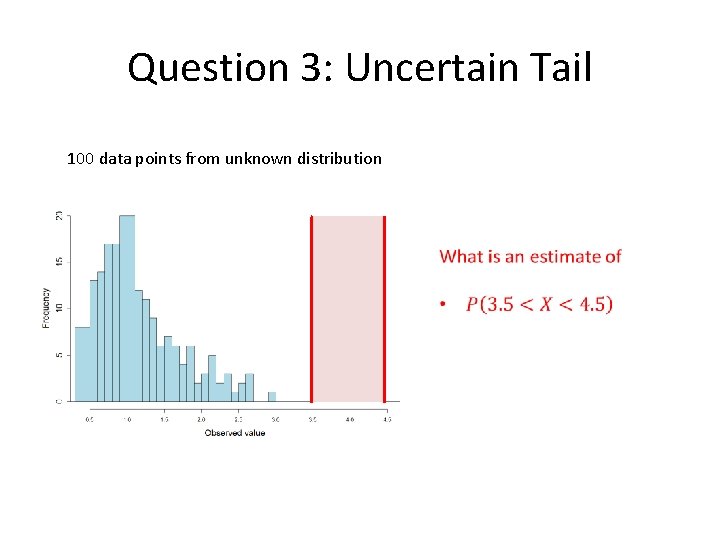
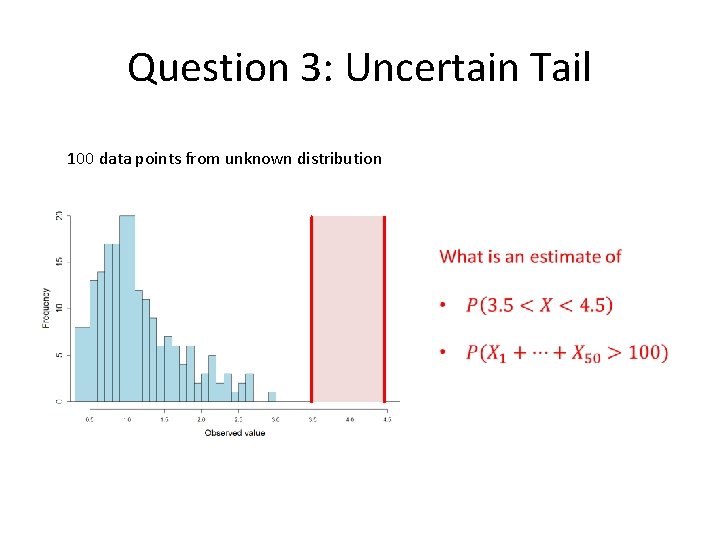
Question 3: Uncertain Tail 100 data points from unknown distribution

Robust Stochastic Modeling Model uncertainty arises due to modeling limitations, presence of risk, lack of data etc. Robust perspective: With all the known information/belief, analyze the worst-case on the unknown

Robust Stochastic Modeling •

Basic Example i. i. d.

Basic Example • i. i. d.

Example 2: Uncertain Dependency i. i. d.

Example 2: Uncertain Dependency

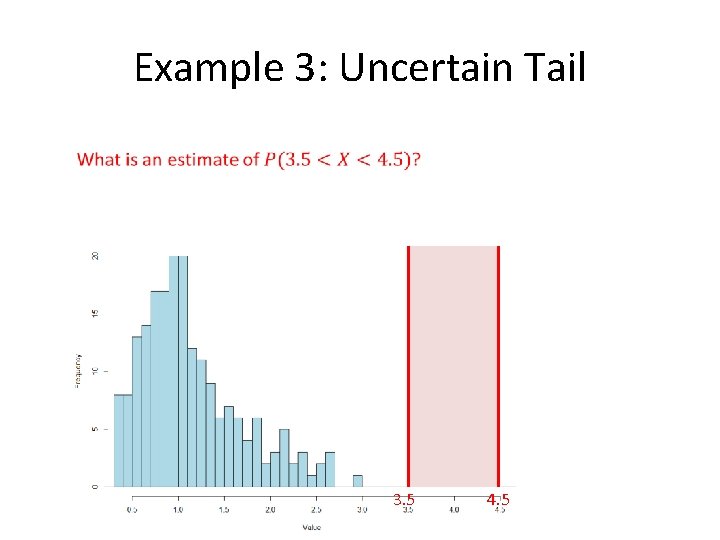
Example 3: Uncertain Tail 3. 5 4. 5

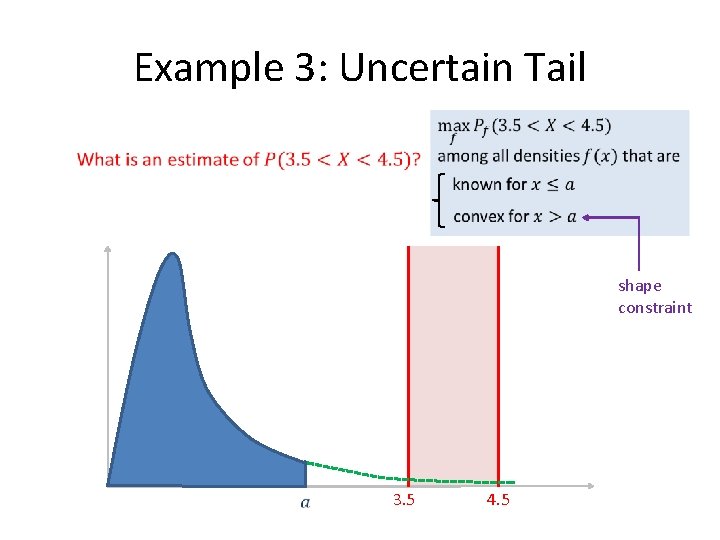
Example 3: Uncertain Tail shape constraint 3. 5 4. 5

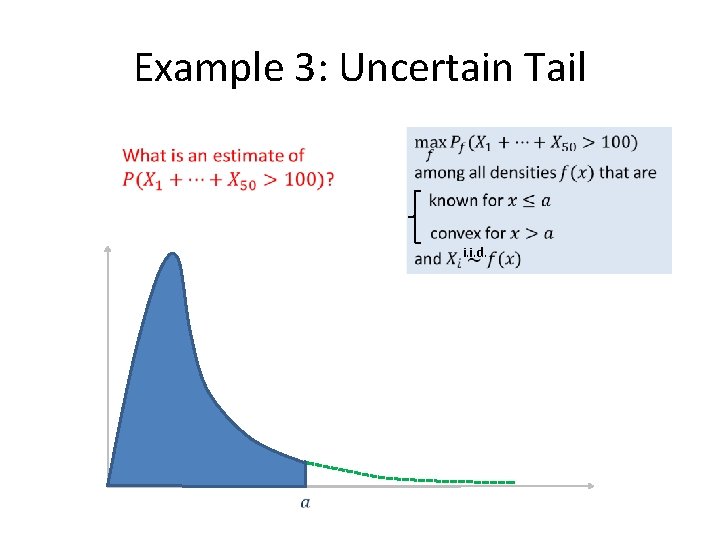
Example 3: Uncertain Tail i. i. d.

Past Literature Area Examples of Works Economics Hansen & Sargent ‘ 01, ’ 08 Finance Glasserman & Xu ’ 13, Lim et al. ‘ 12 Control theory/MDP Petersen et. al. ‘ 00, Nilim & El Ghaoui ‘ 05, Iyengar ’ 05, Jain et. al. ’ 10 (Distributionally) robust optimization Delage & Ye ‘ 10, Goh & Sim ‘ 10, Ben-Tal et. al. ’ 13, Bandi & Bertsimas ’ 12 Robust Monte Carlo Glasserman & Xu ’ 14 Decision analysis/Moment method Smith ‘ 93, ‘ 95, Birge & Wets ’ 87, Bertsimas & Popescu ’ 05, Popescu ‘ 05

Past Literature Area Examples of Works Economics Hansen & Sargent ‘ 01, ’ 08 Finance Glasserman & Xu ’ 13, Lim et al. ‘ 12 Control theory/MDP Petersen et. al. ‘ 00, Nilim & El Ghaoui ‘ 05, Iyengar ’ 05, Jain et. al. ’ 10 (Distributionally) robust optimization Delage & Ye ‘ 10, Goh & Sim ‘ 10, Ben-Tal et. al. ’ 13, Bandi & Bertsimas ’ 12 Robust Monte Carlo Glasserman & Xu ’ 14 Decision analysis/Moment method Smith ‘ 93, ‘ 95, Birge & Wets ’ 87, Bertsimas & Popescu ’ 05, Popescu ‘ 05 Typical focus in the literature: • Tractable convex optimization formulation

Past Literature Area Examples of Works Economics Hansen & Sargent ‘ 01, ’ 08 Finance Glasserman & Xu ’ 13, Lim et al. ‘ 12 Control theory/MDP Petersen et. al. ‘ 00, Nilim & El Ghaoui ‘ 05, Iyengar ’ 05, Jain et. al. ’ 10 (Distributionally) robust optimization Delage & Ye ‘ 10, Goh & Sim ‘ 10, Ben-Tal et. al. ’ 13, Bandi & Bertsimas ’ 12 Robust Monte Carlo Glasserman & Xu ’ 14 Decision analysis/Moment method Smith ‘ 93, ‘ 95, Birge & Wets ’ 87, Bertsimas & Popescu ’ 05, Popescu ‘ 05 Typical focus in the literature: • Tractable convex optimization formulation Challenges in the stochastic modeling contexts: • Non-standard constraints, general objectives • High or infinite dimensionality • Stochastic/simulation-based

Solution Techniques • Asymptotic/sensitivity approach • Simulation optimization methods

A Sensitivity Approach Worst-case formulation for the Basic Example: i. i. d.

A Sensitivity Approach Relaxed worst-case formulation for the Basic Example:

A Sensitivity Approach Relaxed worst-case formulation for the Basic Example: Too conservative…

A Sensitivity Approach Worst-case formulation: i. i. d.

A Sensitivity Approach Worst-case formulation: i. i. d. •

Form of Expansion Coefficients •

Form of Expansion Coefficients • i. i. d.

Form of Expansion Coefficients i. i. d.

Form of Expansion Coefficients i. i. d. Simulation strategy: nested simulation, or nonparametric bootstrap

Numerical Illustration • Worst-case formulation: and i. i. d. Asymptotic approximation

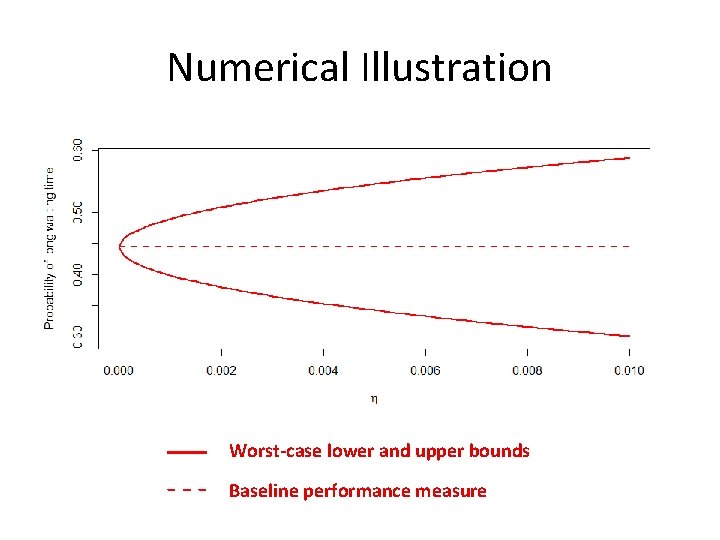
Numerical Illustration Worst-case lower and upper bounds Baseline performance measure

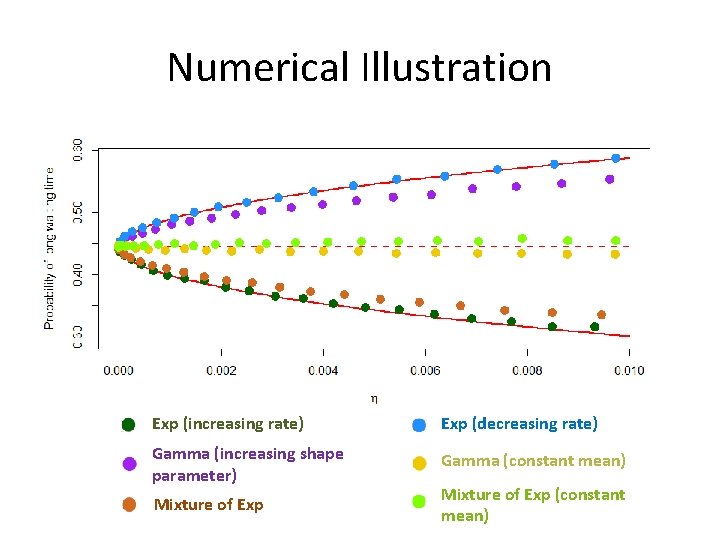
Numerical Illustration Exp (increasing rate) Exp (decreasing rate) Gamma (increasing shape parameter) Gamma (constant mean) Mixture of Exp (constant mean)

Uncertain Dependency

Uncertain Dependency i. i. d.

Uncertain Dependency i. i. d. Simulation strategy: nested simulation + two-way analysis of variance (ANOVA)

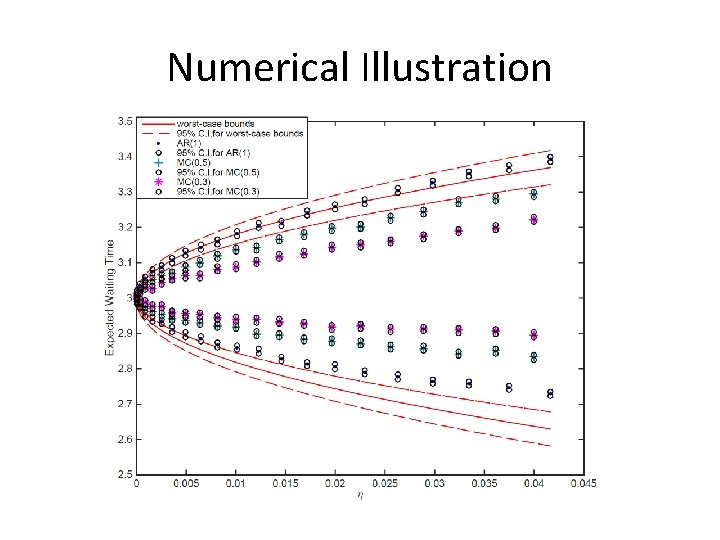
Numerical Illustration

Simulation Optimization Approach Beyond asymptotic approximation?

Simulation Optimization Approach Beyond asymptotic approximation? Numerical scheme for solving local optimum, consisting of: • Gradient estimation: – A “nonparametric” version of likelihood ratio / score function method (Glynn ‘ 90, Reiman & Weiss ’ 89, L’Ecuyer ‘ 90) • Constrained stochastic approximation (SA) via stochastic adaptation of: – Frank-Wolfe (FW) (e. g. , Bertsekas ’ 99, Freund & Grigas ‘ 14) – Mirror descent (MD) (e. g. , Nemirovski ’ 09, Beck & Teboulle ‘ 03)

Gradient Estimation on Space of Probability Distributions i. i. d.

Gradient Estimation on Space of Probability Distributions

Gradient Estimation on Space of Probability Distributions •

Stochastic Approximation on Probability Simplex •

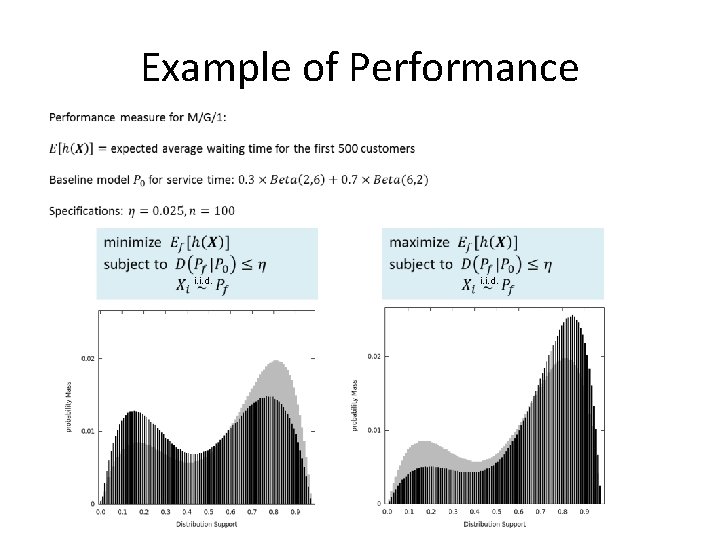
Example of Performance • i. i. d.

Tail Uncertainty The tail extrapolation problem can be reduced into a low-dimensional nonlinear program More general objectives can be locally solved by running FWSA i. i. d.

Discussion Motivation: Model misspecification/uncertainty Main Approach: Optimization over input stochastic models under nonparametric constraints Challenges: Direct solution is intractable for many natural stochastic modeling contexts Methods: Asymptotic approximation, simulation optimization Many open questions: • Calibration of uncertainty sets • Other forms of stochastic uncertainty • System bias • Larger-scale systems • Reducing conservativeness