Model Transportasi Contoh Tabel biaya pengiriman dalam dollar

Model Transportasi
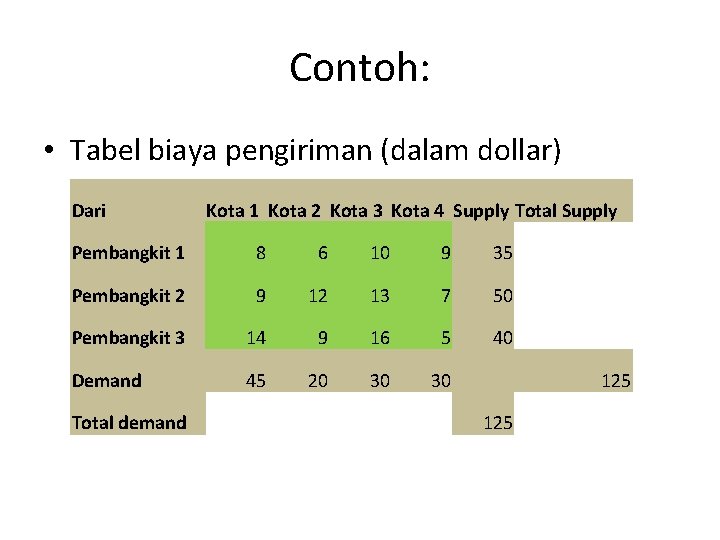
Contoh: • Tabel biaya pengiriman (dalam dollar) Dari Kota 1 Kota 2 Kota 3 Kota 4 Supply Total Supply Pembangkit 1 8 6 10 9 35 Pembangkit 2 9 12 13 7 50 Pembangkit 3 14 9 16 5 40 Demand 45 20 30 30 Total demand 125
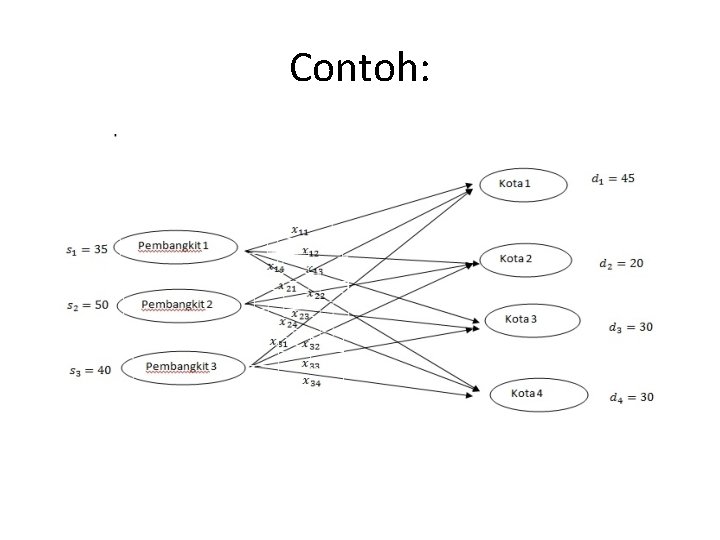
Contoh:

Model Linear

Asumsi • Asumsi, balanced, total supply = total demand • Jika total supply >= total demand • Konsep dummy variable, dengan biaya pengiriman nol ke titik dummy • Jika total supply < total demand: tidak ada solusi feasible. • Dikenakan penalti untuk demand yang tidak terpenuhi
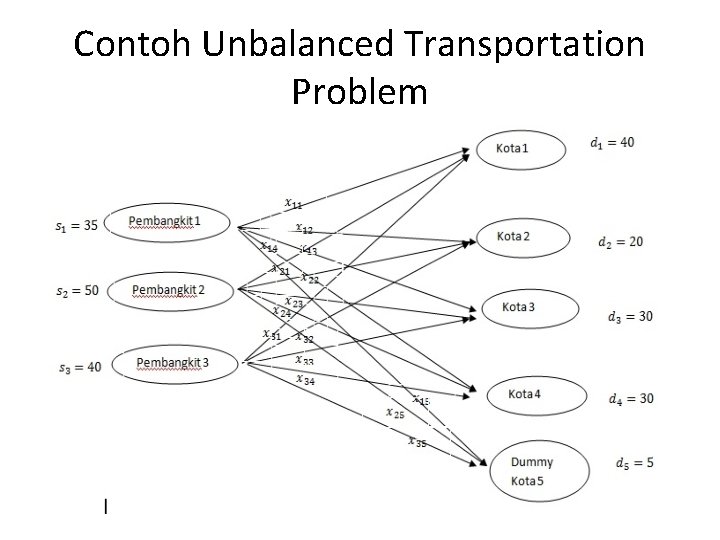
Contoh Unbalanced Transportation Problem

Metode penyelesaian • Dengan m supply points dan n demand points: m+n constraints (kendala) • Northwest corner • Minimum cost • Vogel – Tiga metode terakhir memanfaatkan struktur tabel yang spesifik dari model transportasi • Simplex method* *dengan software optimasi/spreadsheet

Northwest Corner • Mencari solusi feasibel dari sudut utara (north)-barat (west) • Pada sudut north west: Min (total kolom, total baris) • Kelemahan: tidak memanfaatkan biaya • Dapat ditemukan solusi feasibel dengan biaya tidak optimal (terlalu mahal).

Minimum Cost Method • Biaya dilibatkan dalam pemilihan solusi • Solusi paling awal ditentukan dari variabel dengan biaya minimum • Langkah-langkah iterasi serupa dengan metode Northwest Corner, hanya saja pemilihan variable selalu berdasarkan biaya minimum • Alokasikan min(supply, demand) pada sel dgn biaya terkecil

Minimum Cost Method • Kelemahan: – Pada kasus tertentu, ada kemungkinan diperolehnya solusi dengan biaya yang ekstra mahal.

Metode Vogel • Setiap kolom dan baris dikenakan penalti, selisih dari dua biaya terkecil • Variabel awal dipilih dari baris/kolom dengan penalti terbesar, pada biaya minimum – Untuk menghindari dipilihnya variabel dengan biaya yang terlalu besar – Biaya yang besar: penalti besar

Perbandingan ketiga Metode • Metode Northwest corner: paling mudah, tapi tidak mempertimbangkan biaya • Metode Minimum Cost: biaya dilibatkan, tapi ada kasus tertentu dengan dipilihnya biaya termahal • Metode Vogel: proses iterasi lebih rumit, kombinasi solusi menghasilkan biaya terkecil – Pada model transportasi yang kompleks: jumlah iterasi yang lebih sedikit daripada kedua metode sebelumnya.

Metode Simplex • • Formulasi LP, fungsi obyektif dan kendala-2 Solusi dengan spreadsheet, Interpretasi, Analisis sensitivitas
- Slides: 13