Model Sistem dan Model Trafik 2 Pemodelan Ada

Model Sistem dan Model Trafik

2 Pemodelan �Ada dua fasa dalam pemodelan �Pemodelan trafik yang masuk (incoming traffic) model trafik �Pemodelan sistem model sistem

MODEL SYSTEM

4

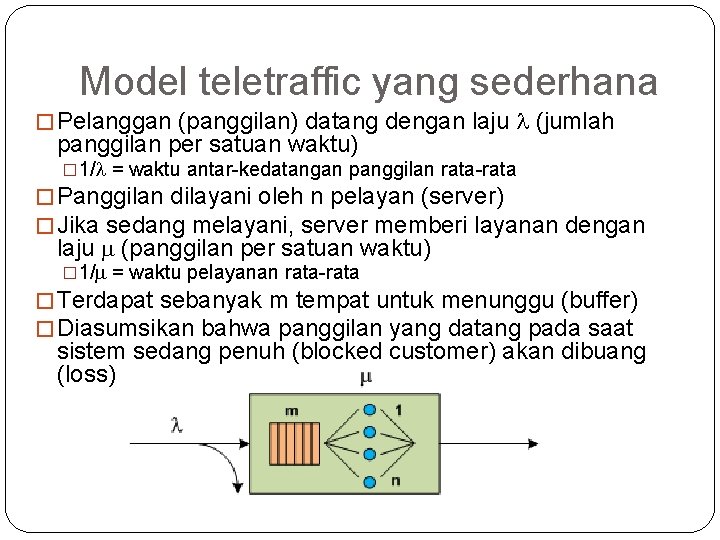
5 Model teletraffic yang sederhana � Pelanggan (panggilan) datang dengan laju (jumlah panggilan per satuan waktu) � 1/ = waktu antar-kedatangan panggilan rata-rata � Panggilan dilayani oleh n pelayan (server) � Jika sedang melayani, server memberi layanan dengan laju m (panggilan per satuan waktu) � 1/m = waktu pelayanan rata-rata � Terdapat sebanyak m tempat untuk menunggu (buffer) � Diasumsikan bahwa panggilan yang datang pada saat sistem sedang penuh (blocked customer) akan dibuang (loss)

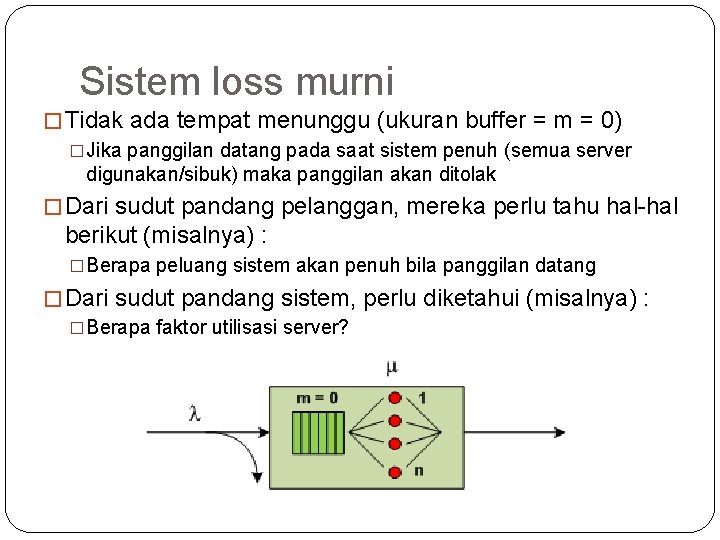
6 Sistem loss murni � Tidak ada tempat menunggu (ukuran buffer = m = 0) �Jika panggilan datang pada saat sistem penuh (semua server digunakan/sibuk) maka panggilan akan ditolak � Dari sudut pandang pelanggan, mereka perlu tahu hal-hal berikut (misalnya) : �Berapa peluang sistem akan penuh bila panggilan datang � Dari sudut pandang sistem, perlu diketahui (misalnya) : �Berapa faktor utilisasi server?

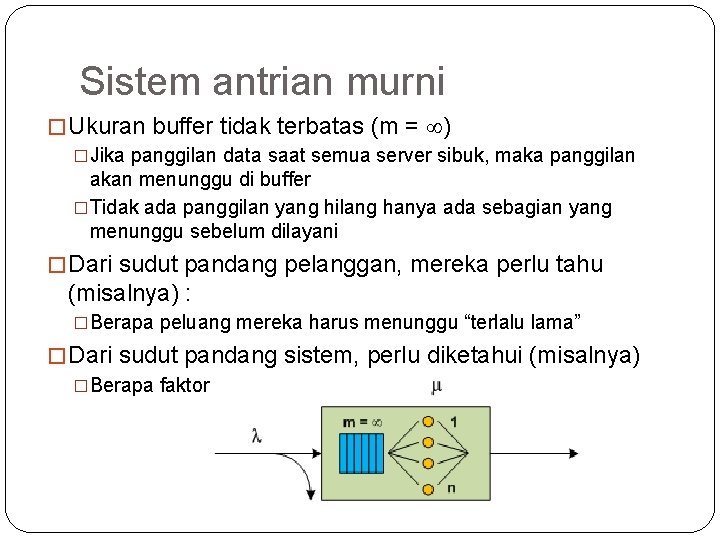
7 Sistem antrian murni � Ukuran buffer tidak terbatas (m = ) �Jika panggilan data saat semua server sibuk, maka panggilan akan menunggu di buffer �Tidak ada panggilan yang hilang hanya ada sebagian yang menunggu sebelum dilayani � Dari sudut pandang pelanggan, mereka perlu tahu (misalnya) : �Berapa peluang mereka harus menunggu “terlalu lama” � Dari sudut pandang sistem, perlu diketahui (misalnya) �Berapa faktor utilisasi server?

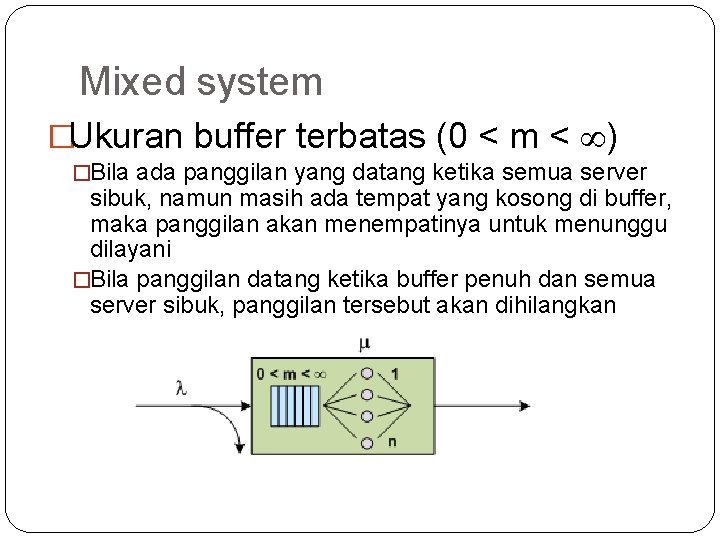
8 Mixed system �Ukuran buffer terbatas (0 < m < ) �Bila ada panggilan yang datang ketika semua server sibuk, namun masih ada tempat yang kosong di buffer, maka panggilan akan menempatinya untuk menunggu dilayani �Bila panggilan datang ketika buffer penuh dan semua server sibuk, panggilan tersebut akan dihilangkan

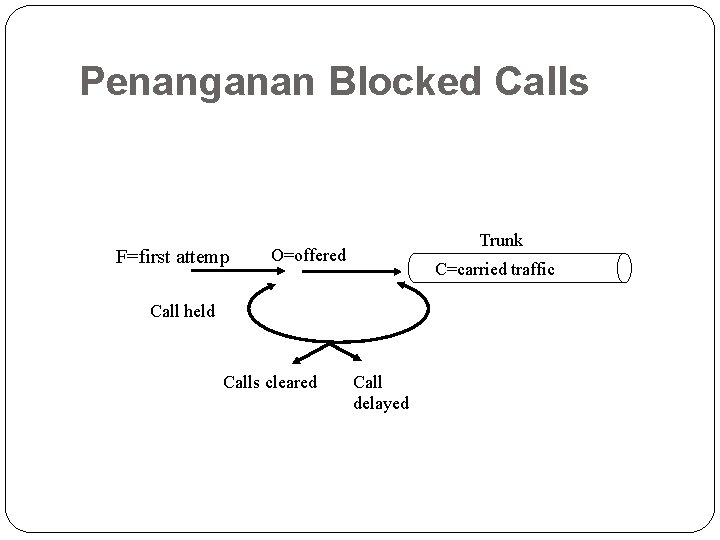
Penanganan Blocked Calls �Penanganan block call menentukan model yang akan dipilih karena penanganan block call yang berbeda menghasilkan beban trafik yang berbeda 9

Penanganan Blocked Calls F=first attemp Trunk O=offered C=carried traffic Call held Calls cleared 10 Call delayed

Penanganan Blocked Calls �Tipe utama dari block call adalah sebagai berikut : �Lost Calls Held (LCH) : Originally LCH was based on theory that all calls introduced to a traffic system were held for a finite amount of time. �Lost Calls Cleared (LCC) : These blocked calls are cleared from the system �Lost Calls Delayed (LCD) : These blocked calls remain on the system until facilities are available to service the call �Lost Calls Retried (LCR): LCR assumes that once a call is blocked, a percentage of the blocked callers retry and all other blocked callers retry until they are serviced. LCR is a derivative of the LCC model and is used in the Extended Erlang B model 11

Types of Blocking Models • Blocked Calls Cleared (BCC) BCC – Blocked calls leave system and do not return – Good approximation for calls in 1 st choice trunk group 12

Types of Blocking Models �Blocked Calls Held (BCH) BCH �Blocked calls remain in the system for the amount of time it would have normally stayed for �If a server frees up, the call picks up in the middle and continues �Not a good model of real world behaviour (mathematical approximation only) �Tries to approximate call reattempt efforts 13

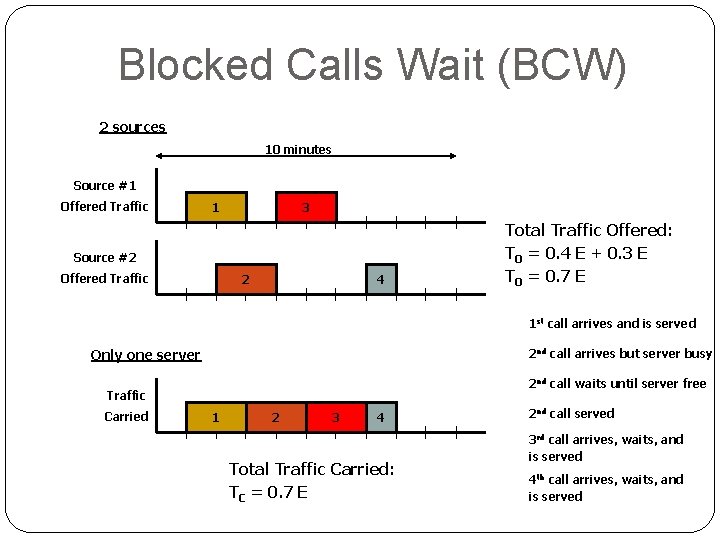
Types of Blocking Models �Blocked Calls Wait (BCW) BCW �Blocked calls enter a queue until a server is available �When a server becomes available, the call’s holding time begins 14

Blocked Calls Cleared (BCC) 2 sources 10 minutes Source #1 Offered Traffic 1 3 Source #2 Offered Traffic 2 4 1 st call arrives and is served Only one server 2 nd call arrives but server already busy Traffic Carried 15 Total Traffic Offered: TO = 0. 4 E + 0. 3 E TO = 0. 7 E 1 2 3 4 Total Traffic Carried: TC = 0. 5 E 2 nd call is cleared 3 rd call arrives and is served 4 th call arrives and is served

Blocked Calls Held (BCH) 2 sources 10 minutes Source #1 Offered Traffic 1 3 Source #2 Offered Traffic 2 4 Total Traffic Offered: TO = 0. 4 E + 0. 3 E TO = 0. 7 E 1 st call arrives and is served Only one server 2 nd call arrives but server busy Traffic Carried 1 2 2 3 4 2 nd call is held until server free 2 nd call is served 16 Total Traffic Carried: TC = 0. 6 E 3 rd call arrives and is served 4 th call arrives and is served

Blocked Calls Wait (BCW) 2 sources 10 minutes Source #1 Offered Traffic 1 3 Source #2 Offered Traffic 2 4 Total Traffic Offered: TO = 0. 4 E + 0. 3 E TO = 0. 7 E 1 st call arrives and is served Only one server 2 nd call arrives but server busy 2 nd call waits until server free Traffic Carried 17 1 2 2 3 4 Total Traffic Carried: TC = 0. 7 E 2 nd call served 3 rd call arrives, waits, and is served 4 th call arrives, waits, and is served

Lost model 18

Overflow System Pada sebuah loss system di circuit switch, sistem bisa saja terdiri dari 2 bagian, yaitu : 1. Primary system = m 1 server 2. Secondary system= m 2 server Bila call masuk pada saat semua server pada primary system occupied, maka akan dilakukan overflow ke secondary system.

MODEL TRAFIK

21

Pemilihan Model Trafik �Untuk menentukan kapasitas yang diperlukan, beban trafik yang diijinkan atau GOS (probabilitas blocking) yang diinginkan diperlukan suatu model trafik. 22

Pemilihan Model Trafik �Dalam pemilihan model trafik, perlu diperhatikan parameter-parameter berikut : �pola kedatangan trafik �trafik yang ditolak (penanganan panggilan yang ditolak) �jumlah dari sumber trafik, �waktu genggam (holding time) 23

Pola kedatangan trafik & distribusi probabilitas kedatangan �Langkah pertama dalam pemilihan model trafik adalah menentukan pola kedatangan trafik. �Pola kedatangan trafik yang utama adalah sebagai berikut : �pola kedatangan panggilan smooth ( smooth call arrival pattern) �pola kedatangan panggilan peak ( peak call arrival pattern) �pola kedatangan random ( random call arrival pattern) 24

Pola kedatangan panggilan smooth (Smooth Call Arrival Pattern) � Smooth atau hypo-exponential traffic terjadi jika tidak terdapat variasi trafik yang besar. Waktu pendudukan (holding time) dan waktu antar kedatangan (interarrival time) dapat diprediksi. 25

Peaked Call Arrival Pattern 26

Random Call Arrival Pattern 27

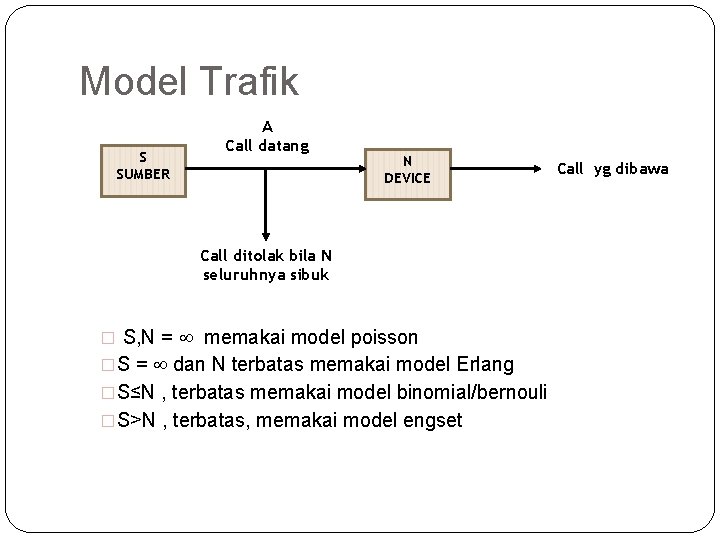
28 Model Trafik S SUMBER A Call datang N DEVICE Call ditolak bila N seluruhnya sibuk � S, N = memakai model poisson �S = dan N terbatas memakai model Erlang �S≤N , terbatas memakai model binomial/bernouli �S>N , terbatas, memakai model engset Call yg dibawa

Pendekatan Analisa Trafik �Deskripsi Trafik �Karakteristik suatu trafik digambarkan oleh : �Pola datang panggilan �Pola lama waktu pendudukan �Disiplin pelayanan : full/limited availability, /delay sistem �Pendekatan matematis yang digunakan adalah : 29 Proses Kelahiran (Birth) Proses Kematian (Death) Datangnya panggilan Berakhirnya pendudukan

Pendekatan Analisa Trafik �Diagram Kondisi n n+1 �Kondisi n n+1 bila ada panggilan datang (kedatangan = Kelahiran) �Kondisi n+1 n bila ada panggilan berakhir (kepergian = kematian) 30

Pendekatan Analisa Trafik �Diagram Transisinya Kedatangan = kelahiran 0 1 2 Kepergian = kematian 31 n State = kondisi dimana dalam berkas tersebut ada n saluran diduduki

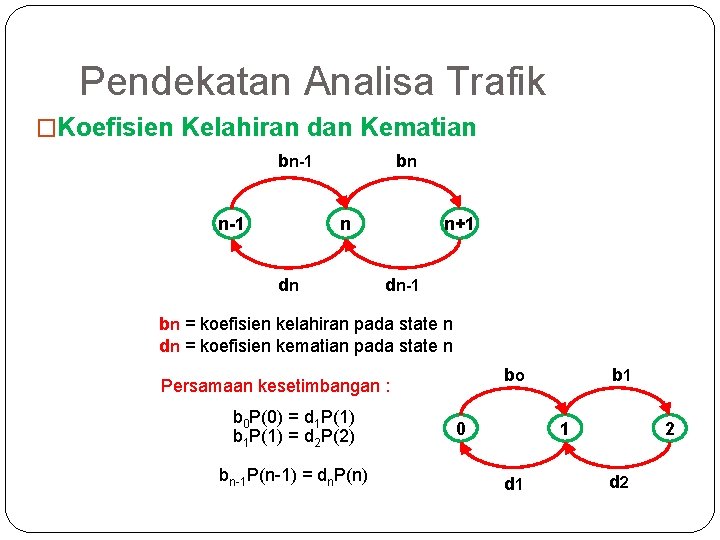
Pendekatan Analisa Trafik �Koefisien Kelahiran dan Kematian bn-1 bn n dn n+1 dn-1 bn = koefisien kelahiran pada state n dn = koefisien kematian pada state n bo Persamaan kesetimbangan : b 0 P(0) = d 1 P(1) b 1 P(1) = d 2 P(2) bn-1 P(n-1) = dn. P(n) 32 0 b 1 1 d 1 2 d 2

33 Distribusi Poisson (1) �Persamaan kesetimbangan ◦ Dalam kesetimbangan statistik, probabilitas kondisi bukan merupakan fungsi waktu. Persamaan kesetimbangannya : bn-1 P(n-1) = dn. P(n) ◦ Kita tinjau koeffisien kelahiran dan kematian �bi (koeffisien kelahiran)= a = �di (koeffisien kematian): bila waktu lamanya pendudukan terdistribusi eksponensial negatif maka di akan sebanding dengan jumlah pendudukan yang ada

34 Distribusi Poisson (2) �Kondisi sistem : �Kedatangan panggilan acak (random arrival) dan independent satu sama lain �Jumlah sumber panggilan tak terhingga �Laju rata-rata datangnya panggilan konstan (a= ) �Tak tergantung jumlah pendudukan yang sudah ada karena sumber panggilan tak terhingga �Jumlah saluran yang melayani tak terhingga dan merupakan berkas sempurna �Setiap panggilan yang datang selalu dapat dilayani �Pola waktu pendudukan terdistribusi exponensial negatif �Waktu pendudukan rata-rata = h = 1/m �Harga rata-rata trafik sama dengan harga variansinya

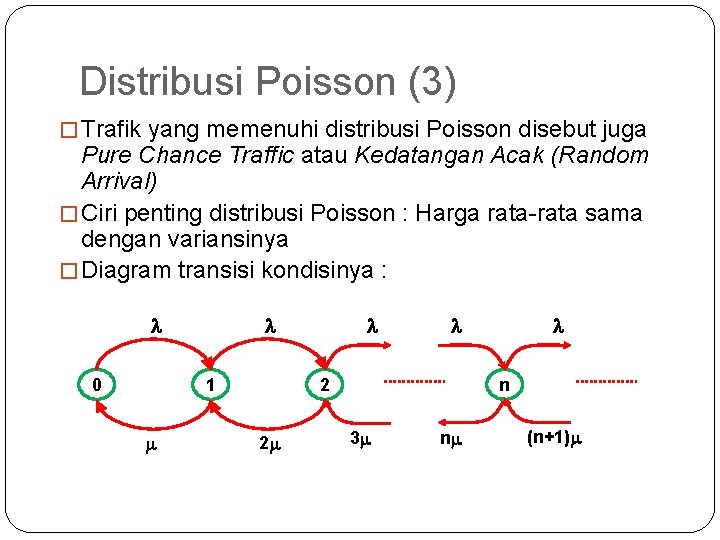
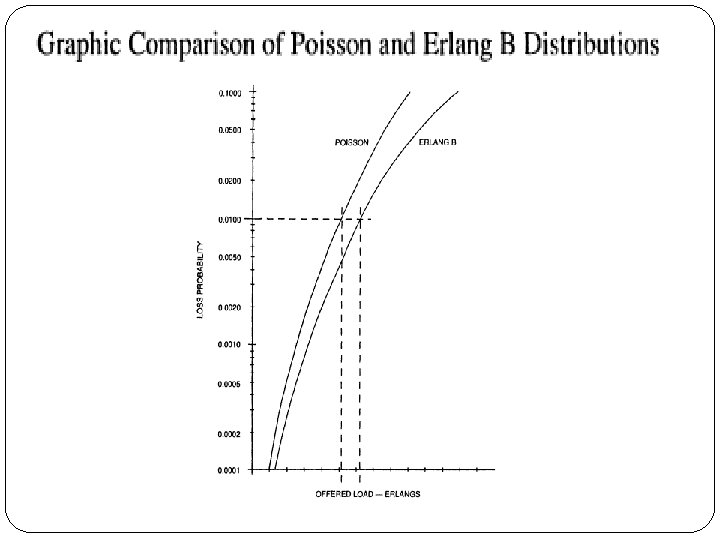
35 Distribusi Poisson (3) � Trafik yang memenuhi distribusi Poisson disebut juga Pure Chance Traffic atau Kedatangan Acak (Random Arrival) � Ciri penting distribusi Poisson : Harga rata-rata sama dengan variansinya � Diagram transisi kondisinya : 0 1 2 2 n 3 n (n+1)

36 Distribusi Poisson (4) � Bila A = . h = /m = trafik yang ditawarkan dan juga merupakan trafik yang dimuat karena trafik terdistribusi Poisson; dan dengan memperhatikan hasil yang terdapat pada slide sebelumnya , kita memperoleh persamaan kesetimbangan sebagai berikut : P(0) = 1 m. P(1) A. P(0) = 1. P(1) A. P(1) = 2. P(2) A. P(2) = 3. P(3). . . A. P(n-1) = n. P(n)

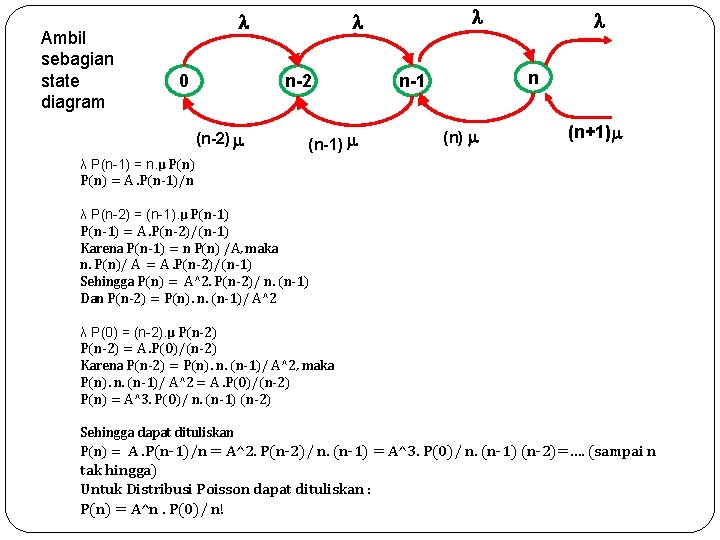
Ambil sebagian state diagram 0 n-2 (n-2) (n-1) n n-1 (n) (n+1) λ P(n-1) = n. μ P(n) = A. P(n-1)/n λ P(n-2) = (n-1). μ P(n-1) = A. P(n-2)/(n-1) Karena P(n-1) = n P(n) /A, maka n. P(n)/ A = A. P(n-2)/(n-1) Sehingga P(n) = A^2. P(n-2)/ n. (n-1) Dan P(n-2) = P(n). n. (n-1)/ A^2 λ P(0) = (n-2). μ P(n-2) = A. P(0)/(n-2) Karena P(n-2) = P(n). n. (n-1)/ A^2, maka P(n). n. (n-1)/ A^2 = A. P(0)/(n-2) P(n) = A^3. P(0)/ n. (n-1) (n-2) Sehingga dapat dituliskan P(n) = A. P(n-1)/n = A^2. P(n-2)/ n. (n-1) = A^3. P(0)/ n. (n-1) (n-2)=…. (sampai n tak hingga) Untuk Distribusi Poisson dapat dituliskan : P(n) = A^n. P(0)/ n!

� Untuk mencari P(0) Peluang total kejadian= 1, sehingga P(i) =1=P(0) +P(1) +P(2) +P(3)+ …. i=0 P(0) = 1 m. P(1) A. P(0) = 1. P(1) A. P(1) = 2. P(2) A. P(2) = 3. P(3). . . A. P(n-1) = n. P(n) Sehingga 1 = P(0). [ 1 + A^2/2! + A^3/3!+…. ] = P(0). e^A P(0) = e^(-A) P(n) = A^n. P(0) / n!

39 Distribusi Poisson(5) � Trafik yang memenuhi distribusi Poisson disebut juga Pure Chance Traffic atau Kedatangan Acak (Random Arrival) � Ciri penting distribusi Poisson : Harga rata-rata sama dengan variansinya � Diagram transisi kondisinya : 0 1 2 2 n 3 n (n+1)

40 Distribusi Poisson(6) �Bila trafik yang terdistribusi Poisson ditawarkan melalui elemen gandeng ke berkas keluar yang jumlah salurannya tak terhingga, maka seluruh trafik yang ditawarkan akan dapat diolah oleh berkas keluar; artinya tidak ada trafik yang hilang (ditolak) �Oleh karena itu trafik yang ditawarkan akan sama dengan trafik yang dimuat oleh berkas keluar atau A=Y

41 Distribusi Poisson

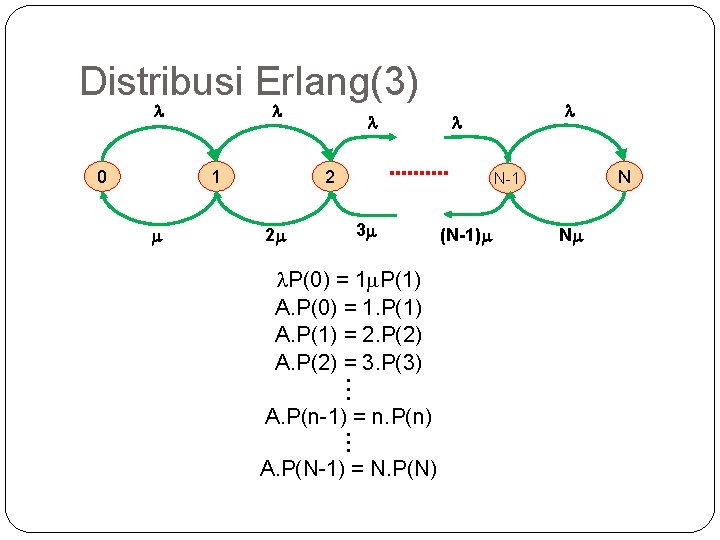
42 Distribusi Erlang(1) � Kondisi sistem : �Kedatangan panggilan acak dan independent satu sama lain �Jumlah sumber panggilan tak terhingga �Laju rata-rata datangnya panggilan konstan (a= ) �Tak tergantung jumlah pendudukan yang sudah ada karena sumber panggilan tak terhingga �Jumlah saluran yang melayani terbatas dan merupakan berkas sempurna �Tidak setiap panggilan yang datang selalu dapat dilayani; panggilan yang datang pada saat semua saluran diduduki akan tidak dapat dilayani; panggilan-panggilan yang tidak dapat dilayani akan dihilangkan (ditolak) Sistem Rugi �Pola waktu pendudukan terdistribusi exponensial negatif �Waktu pendudukan rata-rata = h = 1/m

43 Distribusi Erlang(2) Rumus Rugi Erlang �Dapat digunakan untuk menghitung prosentase panggilan yang hilang bila trafik yang ditawarkan dan jumlah saluran keluar yang menampung diketahui �Penurunan rumus menggunakan diagram transisi kondisi dan persamaan kesetimbangan �Koefisien kelahiran = (konstan) �Koefisien kematian = nm �A = /m

44 Distribusi Erlang(3) 0 1 2 N N-1 3 2 P(0) = 1 m. P(1) A. P(0) = 1. P(1) A. P(1) = 2. P(2) A. P(2) = 3. P(3). . . A. P(n-1) = n. P(n). . . A. P(N-1) = N. P(N) (N-1) N

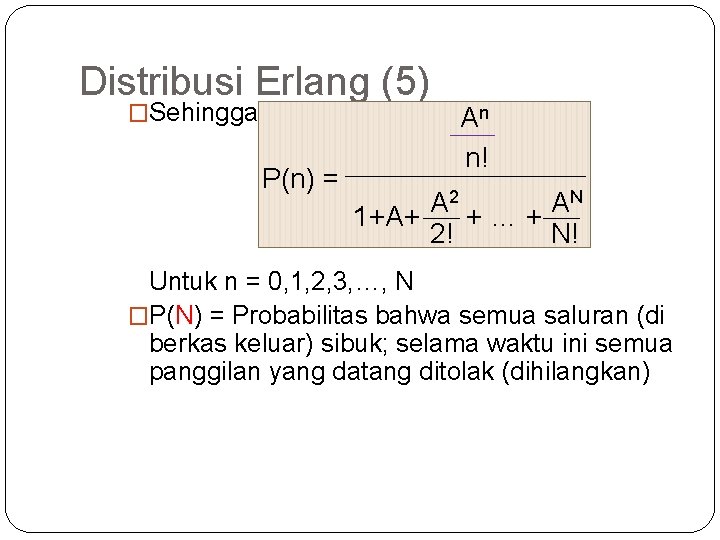
45 Distribusi Erlang(4) � Dari persamaan kesetimbangan tersebut bisa kita peroleh A 2 A An A 3 P(n) = P(n-1) = n(n-1) n. P(0) = P(n-2) = P(n-3)= … n! n(n-1)(n-2) An n! � Jadi P(n) = P(0), dengan n = 0, 1, 2, …, N � Mencari. N P(0) : A 2 A 3 AN 2! 3! + + N! …+ � 1 = n=0 P(n) = P(0) { 1+A+ 1 � Jadi P(0) = N An n=0 n! }

46 Distribusi Erlang (5) �Sehingga P(n) = An n! A 2 AN 1+A+ +…+ 2! N! Untuk n = 0, 1, 2, 3, …, N �P(N) = Probabilitas bahwa semua saluran (di berkas keluar) sibuk; selama waktu ini semua panggilan yang datang ditolak (dihilangkan)

47 Distribusi Erlang(6) �contoh : Pada kelompok sirkit yang terdiri dari 3 sirkit, ditawarkan trafik sebesar 2 erlang. Berapa trafik yang akan lost Trafik lost = R = AB = 2 x 0, 210 = 0, 42 Erlang

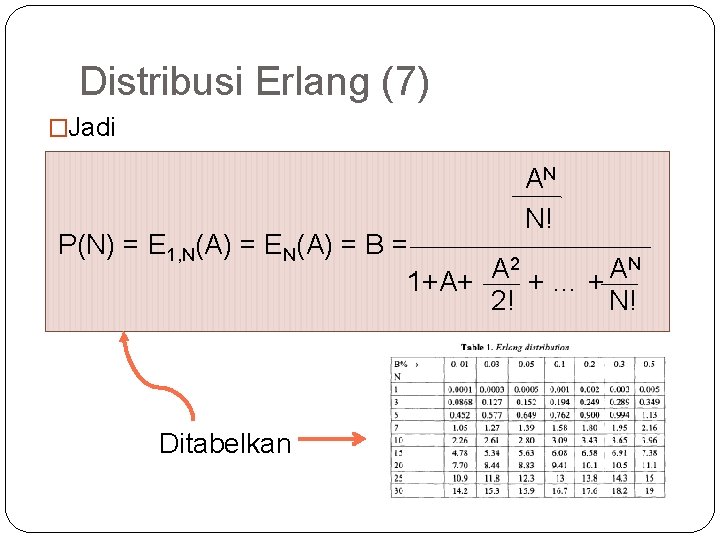
48 Distribusi Erlang (6) �Simbol untuk menyatakan P(N) �E 1, N(A) �EN(A) �B (Blocking) �Rumus Rugi Erlang �Rumus Erlang-B �B(N, A) �Grade of Service (GOS)

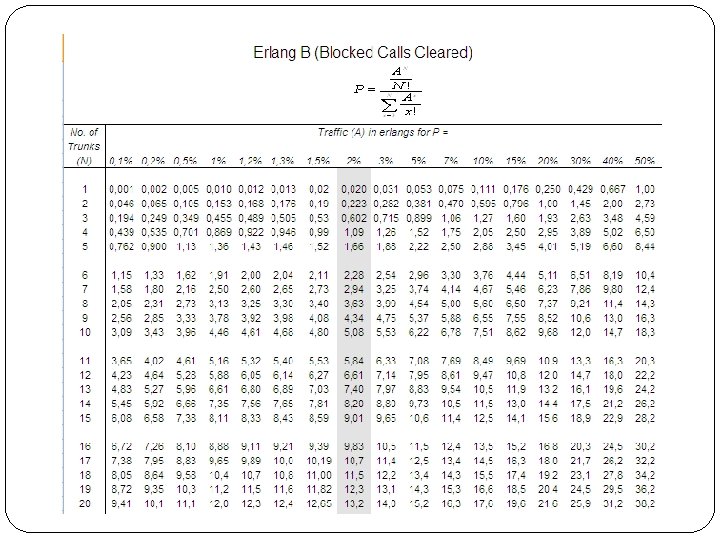
49 Distribusi Erlang (7) �Jadi AN N! P(N) = E 1, N(A) = EN(A) = B = 2 N A A 1+A+ +…+ 2! N! Ditabelkan

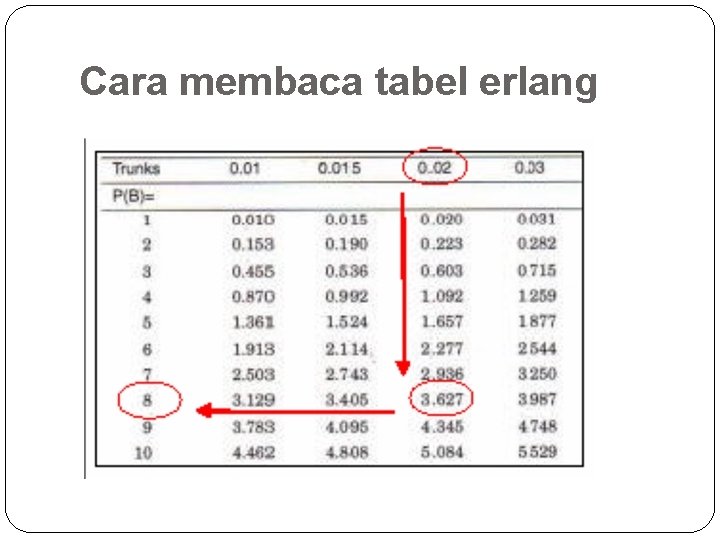
Cara membaca tabel erlang �Berapa trafik yang dapat ditawarkan, jika saluran yang disediakan N=8 dan probabilitas bloking 0. 02 ? �Dari tabel dapat dicari dengan menarik garis untuk N=8 dan Pb=0. 02, dari tabel didapatkan, traffik yg ditawarkan sebesar 3. 627 50

Cara membaca tabel erlang 51

52 Distribusi Erlang (8) Kongesti Waktu dan Kongesti Panggilan �Probabilitas kondisi adalah lamanya waktu suatu kondisi berlangsung dalam jam per jam (jam sibuk), maka �P(N) dapat diartikan sebagai lamanya waktu dimana semua saluran (=N) sibuk berlangsung dalam jam per jamnya (jam sibuk) sehingga �P(N) disebut pula sebagai Kongesti Waktu (Time Congestion) �Dapat pula dikatakan : P(N) adalah bagian waktu dimana N saluran sibuk

53 Distribusi Erlang (9) �Pengertian Kongesti Panggilan = R(N) = Jumlah panggilan yang ditolak Jumlah panggilan selama 1 jam �Atau dengan kata lain : R(N) adalah bagian panggilan yang ditolak �Untuk kedatangan yang acak dan berkas sempurna : P(N) = R(N) ◦ Kongesti panggilan = P(N). /. 1 = P(N) = Kongesti waktu

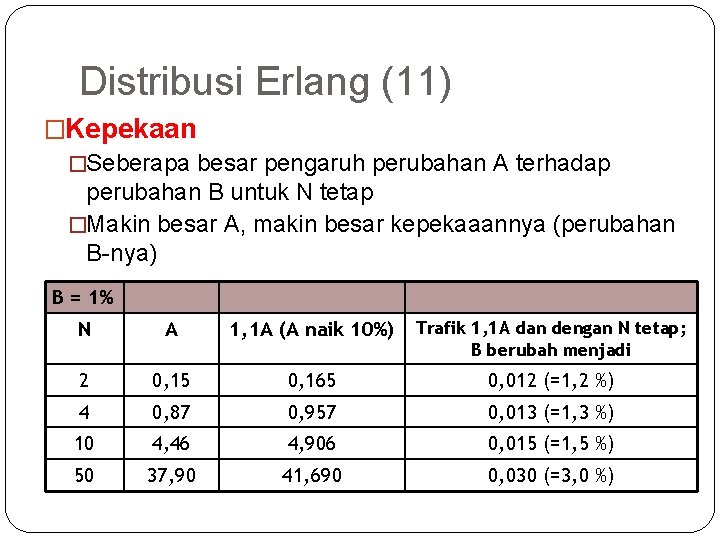
54 Distribusi Erlang (10) Efisiensi dan Kepekaan � Efisiensi (= A/N) �Untuk B tertentu, dengan bertambahnya A, akan diperlukan N yang lebih besar pula �Makin besar A, makin besar (baik) efisiensinya B = 1% N A A/N 2 0, 15 0, 075 4 0, 87 0, 215 10 4, 46 0, 440 50 37, 90 0, 760

55 Distribusi Erlang (11) �Kepekaan �Seberapa besar pengaruh perubahan A terhadap perubahan B untuk N tetap �Makin besar A, makin besar kepekaaannya (perubahan B-nya) B = 1% N A 1, 1 A (A naik 10%) Trafik 1, 1 A dan dengan N tetap; B berubah menjadi 2 0, 15 0, 165 0, 012 (=1, 2 %) 4 0, 87 0, 957 0, 013 (=1, 3 %) 10 4, 46 4, 906 0, 015 (=1, 5 %) 50 37, 90 41, 690 0, 030 (=3, 0 %)

56 Distribusi Erlang (11) Rumus Rekursive Erlang B �Untuk tujuan penghitungan dengan computer, maka rumus erlang B dibuat rumus recursive sbb

57 Distribusi Erlang (11) Rumus Rekursive Erlang B

58 Distribusi Erlang (11) Rumus Rekursive Erlang B sehingga : dengan E 0 (A) =1 A = trafik yang ditawarkan kepada trunk N = jumlah sirkit/server yang melayani

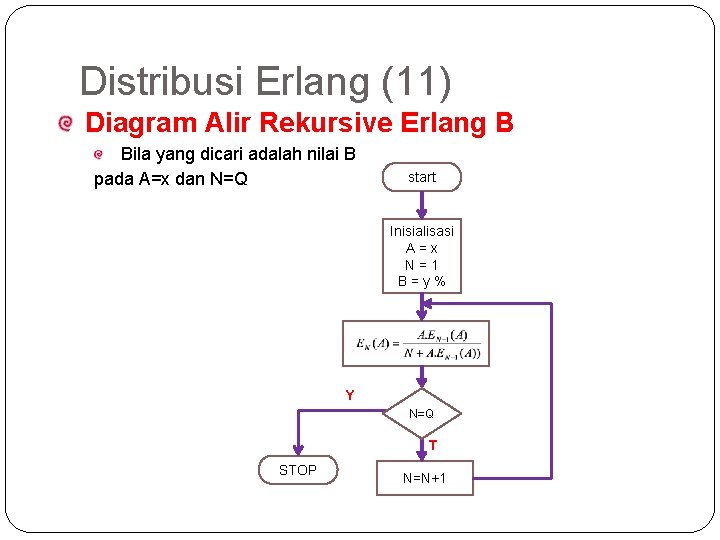
59 Distribusi Erlang (11) Diagram Alir Rekursive Erlang B Bila yang dicari adalah nilai B pada A=x dan N=Q start Inisialisasi A=x N=1 B=y% Y N=Q T STOP N=N+1

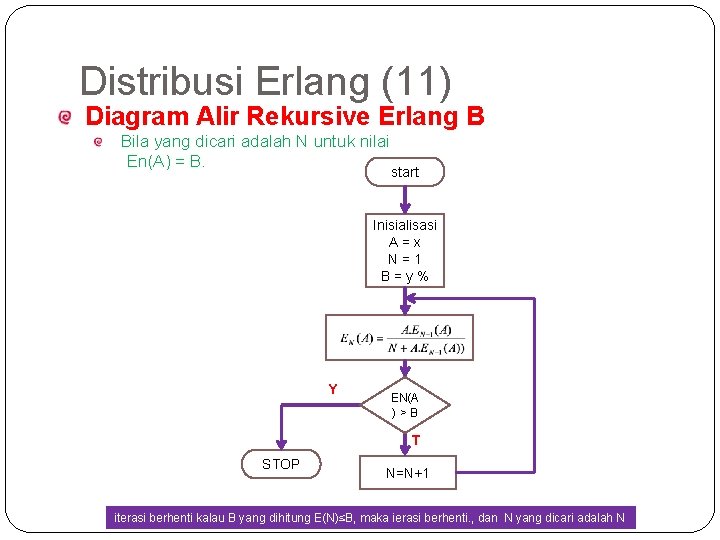
60 Distribusi Erlang (11) Diagram Alir Rekursive Erlang B Bila yang dicari adalah N untuk nilai En(A) = B. start Inisialisasi A=x N=1 B=y% Y EN(A )>B T STOP N=N+1 iterasi berhenti kalau B yang dihitung E(N)≤B, maka ierasi berhenti. , dan N yang dicari adalah N

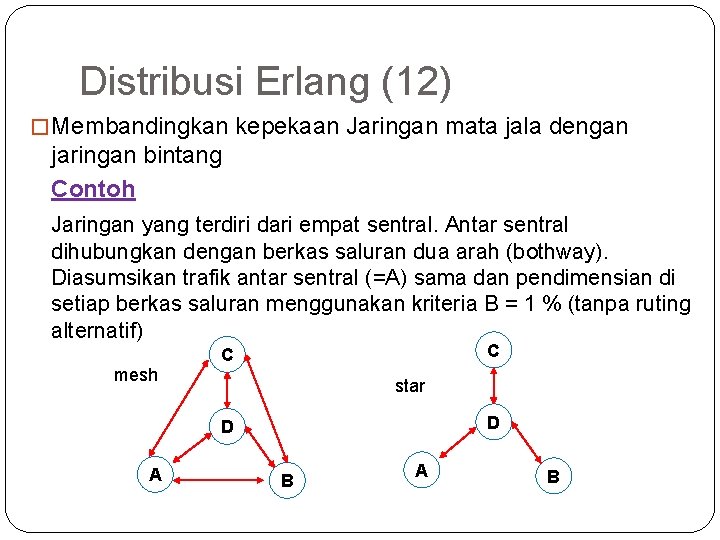
61 Distribusi Erlang (12) � Membandingkan kepekaan Jaringan mata jala dengan jaringan bintang Contoh Jaringan yang terdiri dari empat sentral. Antar sentral dihubungkan dengan berkas saluran dua arah (bothway). Diasumsikan trafik antar sentral (=A) sama dan pendimensian di setiap berkas saluran menggunakan kriteria B = 1 % (tanpa ruting alternatif) mesh C C star D D A B

62 Distribusi Erlang (13) �Pada jaringan star �A = 1 Erlang, maka setiap berkas ditawari 2 Erlang, dengan B = 1%, maka dibutuhkan jumlah saluran untuk setiap berkas sebanyak N = 6 saluran �Bila A dinaikkan menjadi 2 (2 kali lipat), maka tiap berkas akan mengolah trafik 4 Erlang. Bila jumlah saluran pada tiap berkas tetap (N=6), maka B 12%

64 Distribusi Erlang (14) �Pada jaringan mata jala �A = 1 Erlang, maka setiap berkas ditawari 6 Erlang, dengan B = 1%, maka dibutuhkan jumlah saluran dalam setiap berkas sebanyak N = 12 saluran �Bila A dinaikkan menjadi 2 (2 kali lipat), maka tiap berkas akan mengolah trafik 12 Erlang. Bila jumlah saluran pada tiap berkas tetap (N=12), maka B 20% �Jaringan mata jala lebih peka daripada jaringan bintang

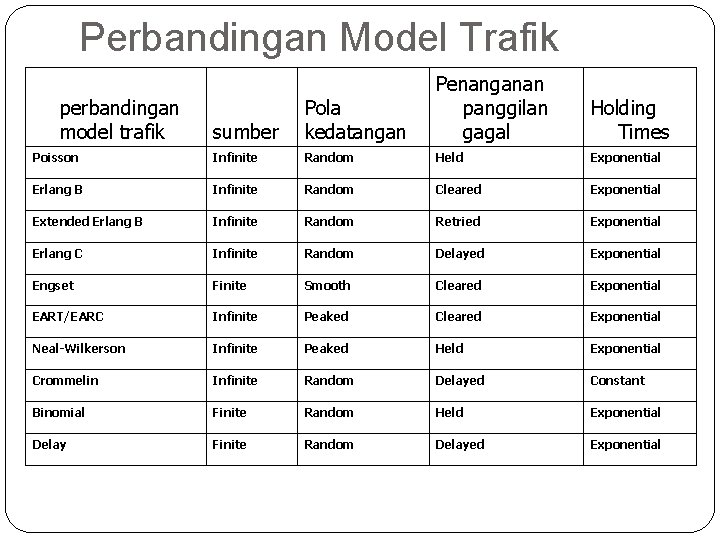
Perbandingan Model Trafik sumber Pola kedatangan Penanganan panggilan gagal Holding Times Poisson Infinite Random Held Exponential Erlang B Infinite Random Cleared Exponential Extended Erlang B Infinite Random Retried Exponential Erlang C Infinite Random Delayed Exponential Engset Finite Smooth Cleared Exponential EART/EARC Infinite Peaked Cleared Exponential Neal-Wilkerson Infinite Peaked Held Exponential Crommelin Infinite Random Delayed Constant Binomial Finite Random Held Exponential Delay Finite Random Delayed Exponential perbandingan model trafik

66

Efficiency of Large Groups (1) • Two trunk groups offered 5 Erlangs each, and B(n, A)=0. 002 5 E n. N 1≈ 13 1=? How many trunks total? From traffic tables, find B(13, 5) 0. 002 5 E n. N 2≈ 13 2=? ntotal = 13 + 13 = 26 trunks Trunk efficiency? Efisiensi = A/N 38. 4% utilization 67

Efficiency of Large Groups (2) • One trunk group offered 10 Erlangs, and B(n, A)=0. 002 How many trunks? 10 E n=20 N=? From traffic tables, find B(20, 10) 0. 002 n = 20 trunks Trunk efficiency? 49. 9% utilization For same gos, we can save 6 trunks! 68

Metode pencarian jalan dalam model erlang B (sentral step by step): �Ada 2 metode, yaitu : �metode homing �metode non homing 69

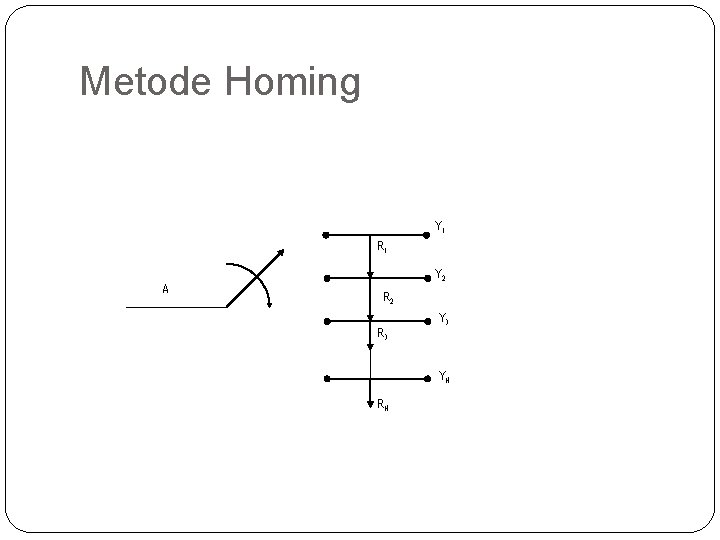
Metode Homing �pada metode homing, pemilihan jalan selalu mulai dari 1, 2, 3……dst. Ini berarti bahwa setelah selector dipakai, wiper selalu dikembalikan ke tempat semula (permulaan jalan keluar ke 1) dan beban atau muatan trafik pada jalan-jalan keluar permulaan lebih besar dari pada jalan-jalan keluar akhir. 70

Metode Homing Y 1 R 1 A Y 2 R 3 YN RN 71

Perhitungan muatan pada homing selector. �Di berkas masuk terdapat trafik A yang ditawarkan ke berkas keluar yang terdiri N saluran. Karena setiap pengetesan jalan keluar selalu dimulai dari jalan ke 1, kemudian jalan ke 2, dst, �maka : �Besarnya R 1, R 2, R 3…RN dapat dihitung dengan rumus rugi erlang. � 72

Perhitungan muatan pada homing selector. �R 1=A-Y 1, Dimana Y 1 adalah besarnya trafik yang dimuat oleh jalan keluar ke 1 �R 2=R 1 -Y 2, Dimana Y 2 adalah besarnya trafik yang dimuat oleh jalan keluar ke 2 �R 3=R 2 -Y 3, Dimana Y 3 adalah besarnya trafik yang dimuat oleh jalan keluar ke 2 � dst �maka Y 1, Y 2, Y 3…. . YN dapat dihitung (jadi muatan tiap saluran dapat dihitung. 73

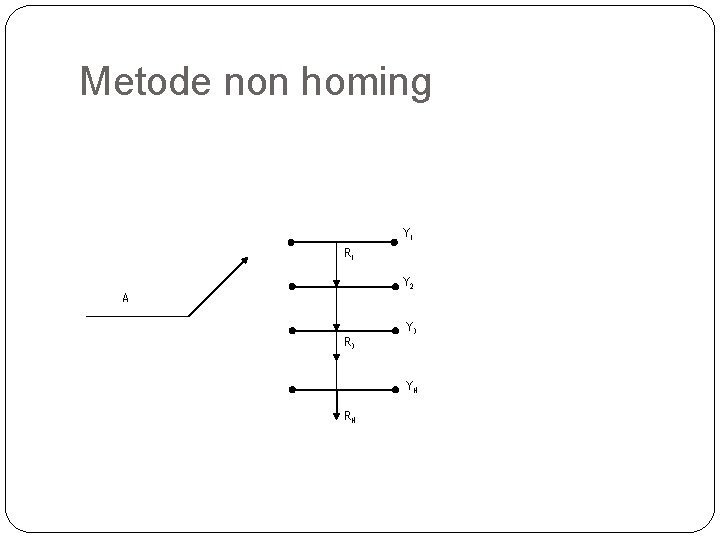
Metode non homing metode non homing �pada metode non homing pemilihan jalur keluar tidak selalu dimulai dari jalan keluar ke 1, tetapi sembarang jalan keluar, tergantung /dimulai dari jalan keluar yang terakhir dipakai. Ini berarti, wiper setelah dipakai (pembubaran) tidak dikembalikan ke tempat semula/jalan keluar ke 1 dan muatan trafiknya merata ke seluruh jalan keluar. 74

Metode non homing Y 1 R 1 Y 2 A R 3 YN RN 75

Perhitungan muatan untuk non homing selector � Karena muatan tiap jalan keluar (saluran) rata/sama maka dapat dihitung sbb: � Maka : Y 1=Y 2=Y 3=Y/N � Dimana � Y (muatan trafik pada berkas keluar) � Y= A-RN � RN= A. B(N, A) 76

Contoh : � Hitung trafik yang dapat dimuat oleh saluran ke 1, 2 dan 3, untuk sistem non homing. Trafik yang ditawarkan sebesar 2 Erlang dan jumlah saluran sebanyak 3. � Penyelesaian : �Y 1=Y 2=Y 3=Y/N= Y/3 �Y = A – R 3 �R 3= A. B(3, A) 77

Model Extended Erlang B �Model trafik Extended Erlang B dikembangkan oleh james jewit dan jacqueline shrago pada pertengahan tahun 1970. �Formula EEB digunakan untuk meningkatkan akurasi formula erlang B yang tidak memperhitungkan panggilan yang mengulang. 78

Model Extended Erlang B � Pada erlang B diasumsikan pemanggil tidak pernah mengulangi panggilannya ketika tidak berhasil dilayani. Panggilan yang mengulang dianggap sebagai panggilan baru, tetapi pada kenyataanya terdapat sejumlah user yang mengulang. �EEB dirancang dengan memperhitungkan panggilan yang mengulang (panggilan yang ditolak mencoba lagi). 79

Asumsi Extended Erlang B �Model trafik Extended Erlang B berdasarkan asumsi sebagai berikut : �Jumlah sumber tidak terbatas �Pola kedatangan trafik acak �Panggilan yang ditolak dihilangkan (Blocked calls cleared) �Tidak ada overflow �Hold times exponentially distributed �Ada panggilan yang mengulang setelah diblok. 80

Asumsi Extended Erlang B �Untuk menghitung probabilitas bloking dengan menggunakan EEB diperlukan : �total trafik yang ditawarkan, �jumlah saluran �prosentase panggilan yang ditolak mencoba lagi (0% s/d 100 %). 81

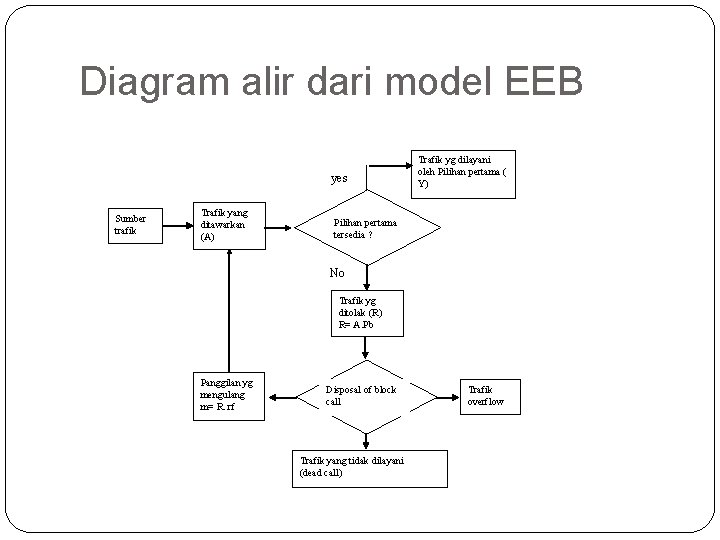
Diagram alir dari model EEB yes Sumber trafik Trafik yang ditawarkan (A) Trafik yg dilayani oleh Pilihan pertama ( Y) Pilihan pertama tersedia ? No Trafik yg ditolak (R) R= A. Pb Panggilan yg mengulang m= R. rf Disposal of block call Trafik yang tidak dilayani (dead call) 82 Trafik overflow

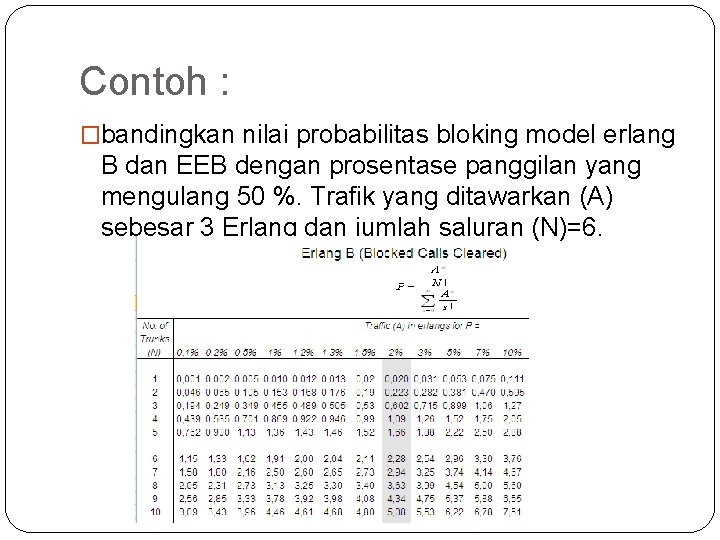
Contoh : �bandingkan nilai probabilitas bloking model erlang B dan EEB dengan prosentase panggilan yang mengulang 50 %. Trafik yang ditawarkan (A) sebesar 3 Erlang dan jumlah saluran (N)=6. 83

contoh �Dengan menggunakan model EEB, perhitungan probabilitas bloking dengan cara iterasi. Beberapa kali iterasi harus dilakukan untuk mendapatkan nilai probabilitas bloking yang dimaksud. Langkah-langkah perhitungan dengan menggunakan model EEB adalah sebagai berikut : �Pertama, hitung probabilitas bloking model erlang B untuk trafik yang ditawarkan sebesar A dan jumlah saluran sebanyak N �Kedua, iterasi perhitungan sampai probabilitas blocking menjadi stabil. Lihat contoh tabel. 84

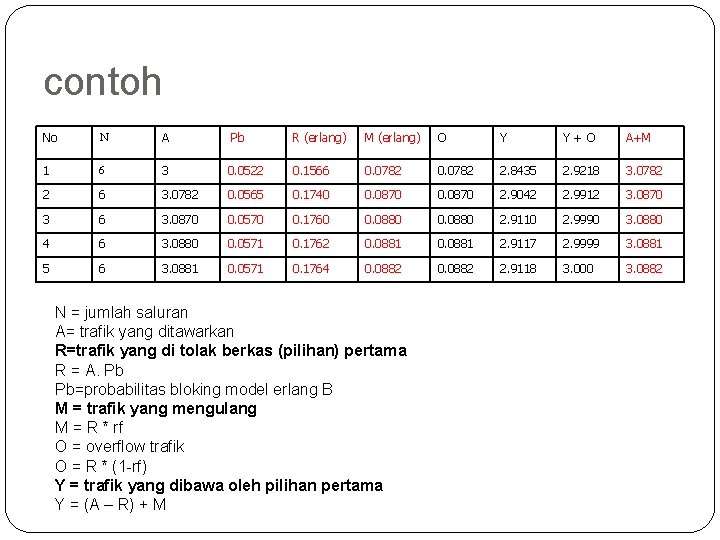
contoh 85 No N A 1 6 3 2 6 3 Pb R (erlang) M (erlang) O Y Y+O A+M 0. 0522 0. 1566 0. 0782 2. 8435 2. 9218 3. 0782 0. 0565 0. 1740 0. 0870 2. 9042 2. 9912 3. 0870 6 3. 0870 0. 0570 0. 1760 0. 0880 2. 9110 2. 9990 3. 0880 4 6 3. 0880 0. 0571 0. 1762 0. 0881 2. 9117 2. 9999 3. 0881 5 6 3. 0881 0. 0571 0. 1764 0. 0882 2. 9118 3. 000 3. 0882 N = jumlah saluran A= trafik yang ditawarkan R=trafik yang di tolak berkas (pilihan) pertama R = A. Pb Pb=probabilitas bloking model erlang B M = trafik yang mengulang M = R * rf O = overflow trafik O = R * (1 -rf) Y = trafik yang dibawa oleh pilihan pertama Y = (A – R) + M

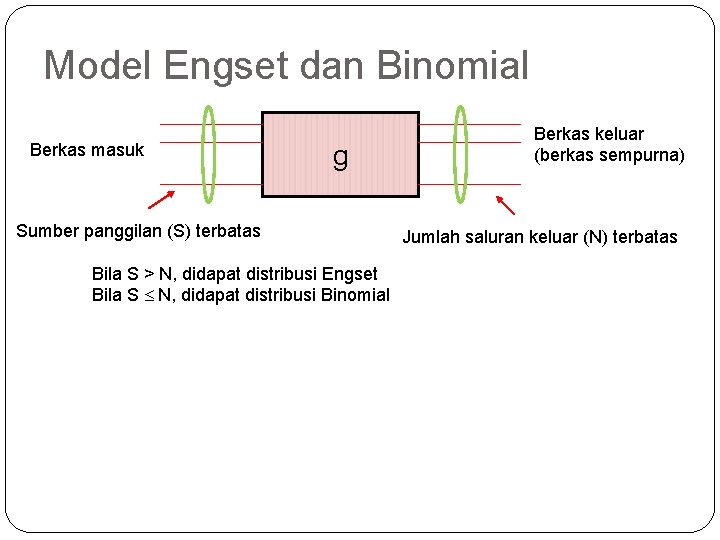
Model Engset dan Binomial Berkas masuk g Sumber panggilan (S) terbatas Bila S > N, didapat distribusi Engset Bila S N, didapat distribusi Binomial Berkas keluar (berkas sempurna) Jumlah saluran keluar (N) terbatas

Model Engset Berkas masuk Berkas keluar Switching network s = terbatas n = terbatas Persamaan engset mirip dengan formula erlang B, tetapi terdapat satu perbedaan yaitu jumlah pemanggil (panggilan) yang terbatas, jadi persamaan engset digunakan ketika jumlah populasi kecil (kurang dari 200). Untuk populasi yang besar, persamaan engset dan erlang B memberikan hasil yang sama ( buktikan !) 87

Asumsi Model Engset �Model Engset berdasarkan pada asumsi berikut : �Jumlah sumber yang terbatas �Pola kedatangan trafik yang terbatas �Panggilan yang ditolak dihilangkan (block call cleared) �Holding time terdistribusi eksponensial 88

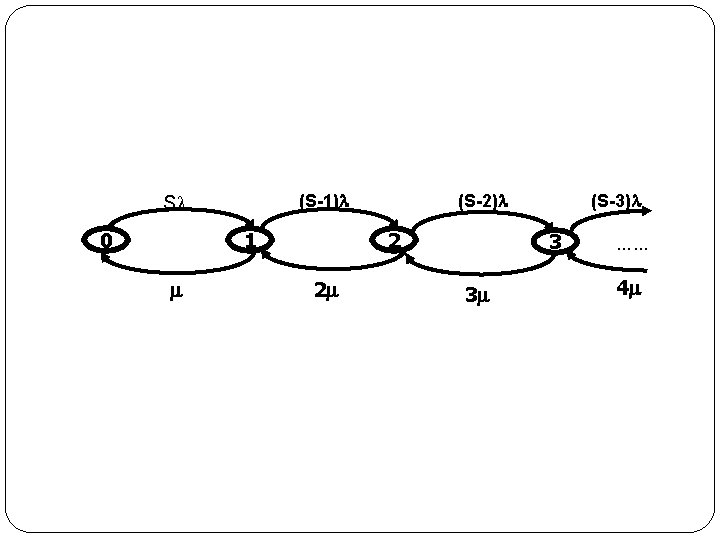
(S-1) S 0 1 (S-2) 2 2 (S-3) 3 3 …… 4

90 Persamaan kesetimbangan � Persamaan kesetimbangan : (s-n) P(n)=(n+1)µ P(n+1) Untuk n=0 s. P(0)=µP(1)=(s. /µ) P(0), dimana /µ =A (intensitas trafik) P(1)=s. A. P(0) Untuk n=1 (s-1) P(1)=2µP(2)=((s-1) /2µ) P(1) P(2)=((s-1) A/2 ) s A P(0) P(2)=(s-1)s. A 2/2 P(0)

91 Persamaan kesetimbangan Untuk n=2 (s-2) P(2)=3µP(3)=(s-2) /3µ. P(2) P(3)=(s-2) A/3 (s-1)s. A 2/2 P(0) P(3)=(s-2) (s-1)s. A 3/3! P(0)

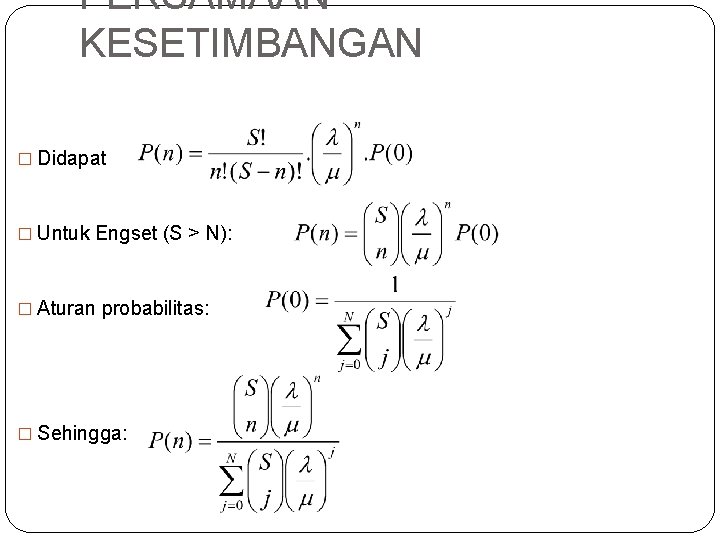
PERSAMAAN KESETIMBANGAN � Didapat � Untuk Engset (S > N): � Aturan probabilitas: � Sehingga:

93 Distribusi Engset �Bila n=N , maka P(N) merupakan probabilitas semua saluran sibuk (Kongesti waktu) = Probabilitas kondisi N �Kongesti panggilan : jumlah panggilan yang ditolak dibagi dengan jumlah seluruh panggilan yang datang �Jumlah panggilan yang ditolak (dlm. 1 jam) : (S-N). P(N) N �Jumlah seluruh panggilan yang datang (dalam 1 (S-j). P(j) jam) : j=0

�Call congestion: �Bila jumlah sumber tak berhingga, P(N) = R(N)

BINOMIAL (BERNOULLI) � Untuk Binomial (S ≤ N) � Dalam hal ini tidak ada kehilangan trafik � � Persamaan normal:

�Hitung probabilitas bloking pada system PABX jika terdapat 2 panggilan per menit, PABX tersebut terdapat 3 saluran dan 5 pelanggan. , PABX tersebut mampu melayani 1 panggilan per menit

HAPPY LEARNING !!