Model Selection and Validation All models are wrong

Model Selection and Validation “All models are wrong; some are useful. ” George E. P. Box Some slides were taken from: • J. C. Sapll: MODELING CONSIDERATIONS AND STATISTICAL INFORMATION • J. Hinton: Preventing overfitting • Bei Yu: Model Assessment

Overfitting • The training data contains information about the regularities in the mapping from input to output. But it also contains noise – The target values may be unreliable. – There is sampling error. There will be accidental regularities just because of the particular training cases that were chosen. • When we fit the model, it cannot tell which regularities are real and which are caused by sampling error. – So it fits both kinds of regularity. – If the model is very flexible it can model the sampling error really well. This is a disaster.

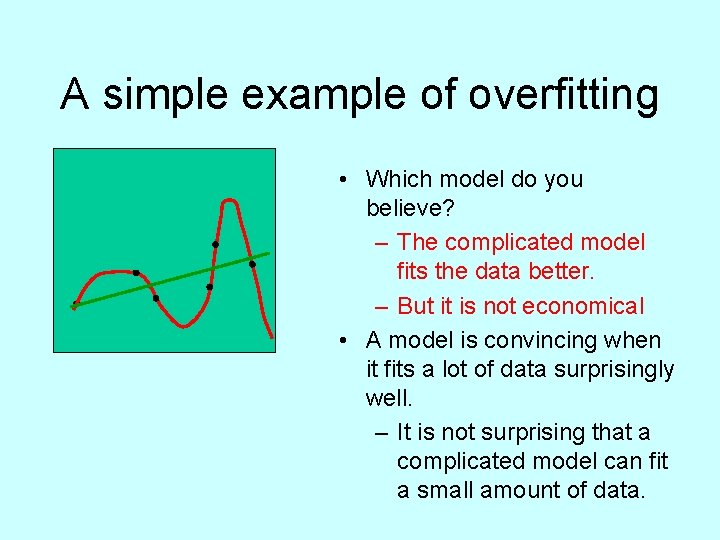
A simple example of overfitting • Which model do you believe? – The complicated model fits the data better. – But it is not economical • A model is convincing when it fits a lot of data surprisingly well. – It is not surprising that a complicated model can fit a small amount of data.

Generalization • The objective of learning is to achieve good generalization to new cases, otherwise just use a look-up table. • Generalization can be defined as a mathematical interpolation or regression over a set of training points: f(x) x

Generalization • Over-Training is the equivalent of over-fitting a set of data points to a curve which is too complex • Occam’s Razor (1300 s, English Logician): – “plurality should not be assumed without necessity” • The simplest model which explains the majority of the data is usually the best

Generalization Preventing Over-training: • Use a separate test or tuning set of examples • Monitor error on the test set as network trains • Stop network training just prior to over-fit error occurring - early stopping or tuning • Number of effective weights is reduced • Most new systems have automated early stopping methods

Generalization Weight Decay: an automated method of effective weight control • Adjust the bp error function to penalize the growth of unnecessary weights: where: = weight -cost parameter is decayed by an amount proportional to its magnitude; those not reinforced => 0

Formal Model Definition • Assume model z = h(x, ) + v, where z is output, h(·) is some function, x is input, v is noise, and is vector of model parameters A fundamental goal is to take n data points and estimate , forming 13 -8

Model Error Definition • Given a data set [xi, yi], i = 1, . . , n • Given a model output h(x, n), where n is taken from some family of parameters, the sum squared errors (SSE, MSE) is Σi [yi - h(xi, n)]2, • The likelihood is Πi. P(h(xi, n)|xi) 13 -9

Error surface as a function of Model parameters can look like this 13 -10

Error surface can also look like this Which one is better? 13 -11

Properties of the error surfaces • The first surface is rough, thus a small change in parameter space can lead to large change in error • Due to the steepness of the surface, a minimum can be found, although a gradient-descent optimization algorithm can get stuck in local minima • The second is very smooth thus, large change in parameter set does not lead to much change in model error • In other words, it is expected that generalization performance will be similar to performance on a test set 13 -12

Parameter stability • Finer detail: while the surface is very smooth, it is impossible to get to the true minima. • Suggests that models that penalize on smoothness may be misleading. • Breiman (1992) has shown that even in simple problems and simple nonlinear models, the degree of generalization is strongly dependent on the stability of the parameters. 13 -13

Bias-Variance Decomposition • Assume: • Bias-Variance Decomposition: • K-NN: • Linear fit: – Ridge Regression: 13 -14

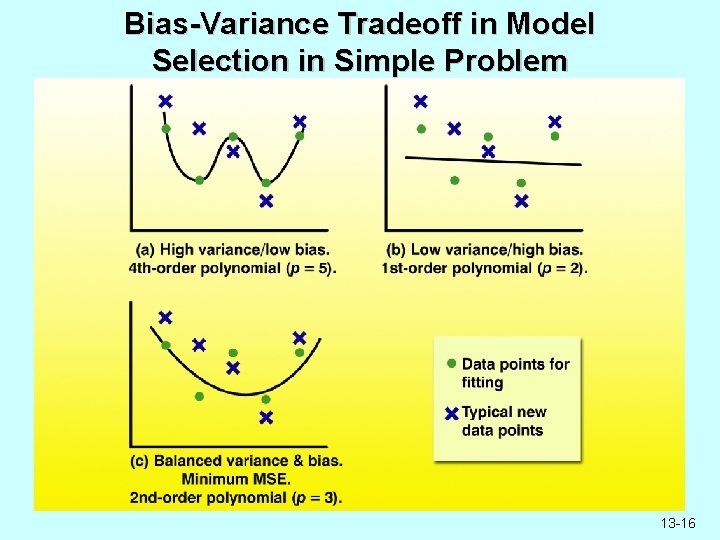
Bias-Variance Decomposition • The MSE of the model at a fixed x can be decomposed as: E{[h(x, ) E(z|x)]2 |x} = E{[h(x, ) E(h(x, ))]2|x} + [E(h(x, )) E(z|x)]2 = variance at x + (bias at x)2 where expectations are computed w. r. t. • Above implies: Model too simple High bias/low variance Model too complex Low bias/high variance 13 -15

Bias-Variance Tradeoff in Model Selection in Simple Problem 13 -16

Model Selection • The bias-variance tradeoff provides conceptual framework for determining a good model – bias-variance tradeoff not directly useful • Many methods for practical determination of a good model – AIC, Bayesian selection, cross-validation, minimum description length, V-C dimension, etc. • All methods based on a tradeoff between fitting error (high variance) and model complexity (low bias) • Cross-validation is one of the most popular model fitting methods 13 -17

Cross-Validation • Cross-validation is a simple, general method for comparing candidate models – Other specialized methods may work better in specific problems • Cross-validation uses the training set of data • Does not work on some pathological distributions • Method is based on iteratively partitioning the full set of training data into training and test subsets • For each partition, estimate model from training subset and evaluate model on test subset • Select model that performs best over all test subsets 13 -18

Division of Data for Cross-Validation with Disjoint Test Subsets 13 -19

Typical Steps for Cross-Validation Step 0 (initialization) Determine size of test subsets and candidate model. Let i be counter for test subset being used. Step 1 (estimation) For the i th test subset, let the remaining data be the i th training subset. Estimate from this training subset. Step 2 (error calculation) Based on estimate for from Step 1 (i th training subset), calculate MSE (or other measure) with data in i th test subset. Step 3 (new training / test subset) Update i to i + 1 and return to step 1. Form mean of MSE when all test subsets have been evaluated. Step 4 (new model) Repeat steps 1 to 3 for next model. Choose model with lowest mean MSE as best. 13 -20

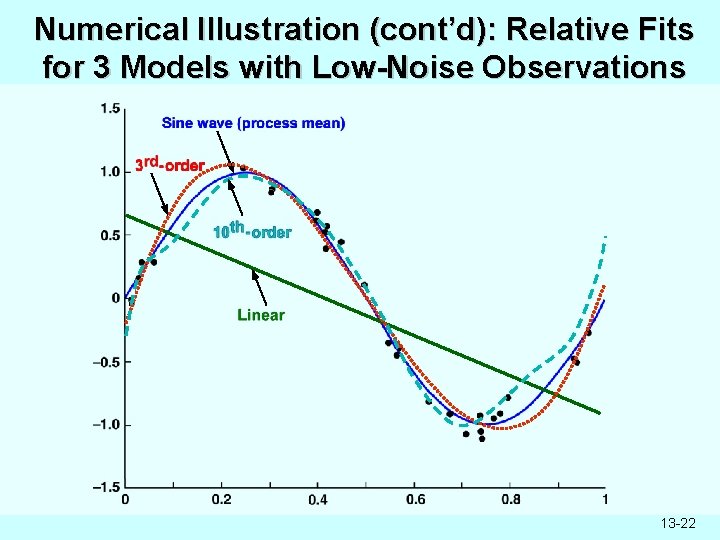
Numerical Illustration of Cross-Validation (Example 13. 4 in ISSO) • Consider true system corresponding to a sine function of the input with additive normally distributed noise • Consider three candidate models – Linear (affine) model – 3 rd-order polynomial – 10 th-order polynomial • Suppose 30 data points are available, divided into 5 disjoint test subsets • Based on RMS error (equiv. to MSE) over test subsets, 3 rd-order polynomial is preferred • See following plot 13 -21

Numerical Illustration (cont’d): Relative Fits for 3 Models with Low-Noise Observations 13 -22

Standard approach to Model Selection • Optimize concurrently the likelihood or mean squared error together with a complexity penalty. • Some penalties: norm of the weight vector, smoothness, number of terminating leaves (in CART), variance weights, cross validation. . . etc. • Spend most computational time on optimizing the parameter solution via sophisticated Gradient descent methods or even global-minimum seeking methods. 13 -23

Alternative approach MDL based model selection Later 13 -24

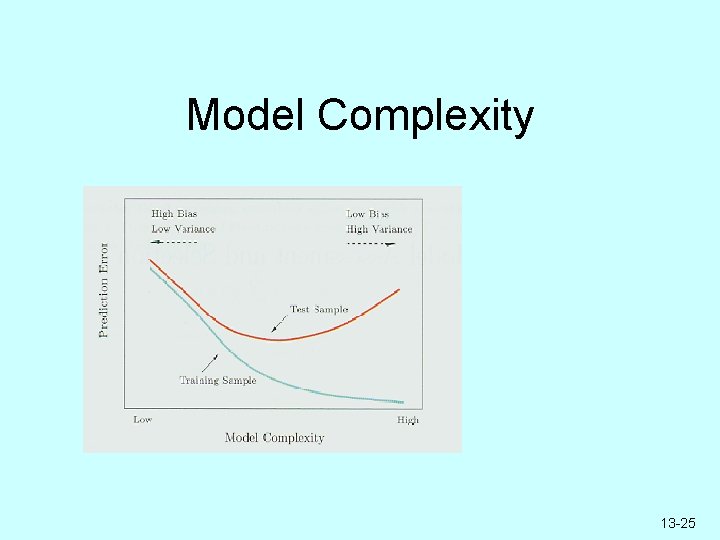
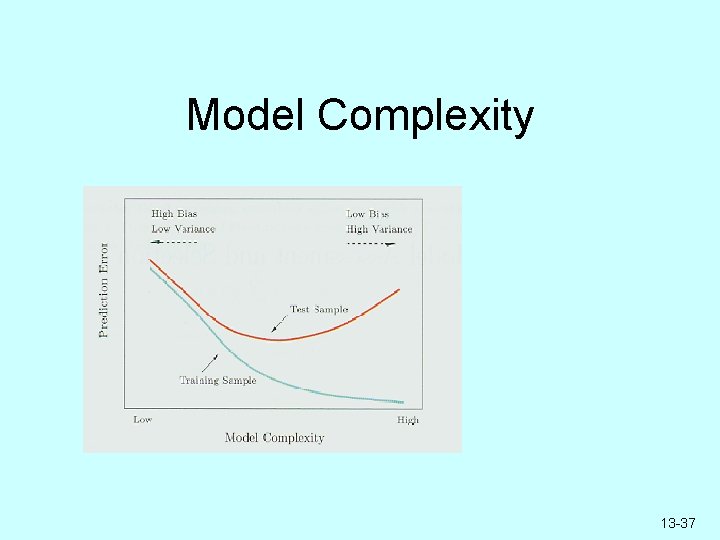
Model Complexity 13 -25

Preventing overfitting • Use a model that has the right capacity: – enough to model the true regularities – not enough to also model the spurious regularities (assuming they are weaker). • Standard ways to limit the capacity of a neural net: – Limit the number of hidden units. – Limit the size of the weights. – Stop the learning before it has time to over-fit. 13 -26

Limiting the size of the weights • Weight-decay involves adding an extra term to the cost function that penalizes the squared weights. – Keeps weights small unless they have big error derivatives. C w 13 -27

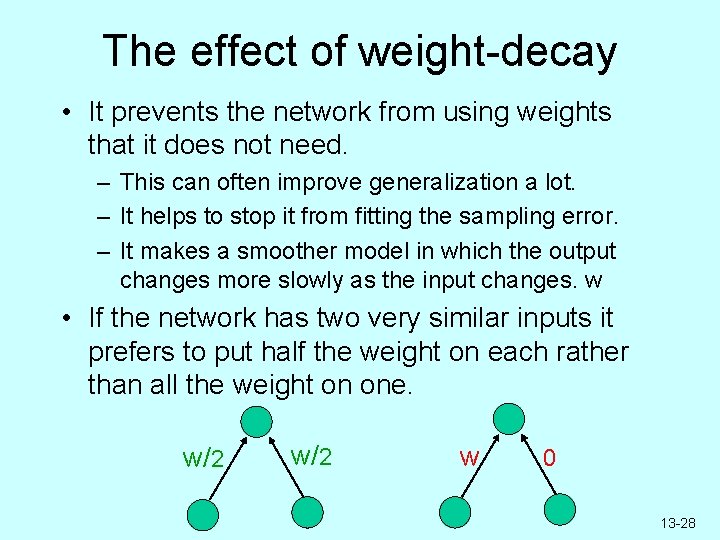
The effect of weight-decay • It prevents the network from using weights that it does not need. – This can often improve generalization a lot. – It helps to stop it from fitting the sampling error. – It makes a smoother model in which the output changes more slowly as the input changes. w • If the network has two very similar inputs it prefers to put half the weight on each rather than all the weight on one. w/2 w 0 13 -28

Model selection • How do we decide which limit to use and how strong to make the limit? – If we use the test data we get an unfair prediction of the error rate we would get on new test data. – Suppose we compared a set of models that gave random results, the best one on a particular dataset would do better than chance. But it wont do better than chance on another test set. • So use a separate validation set to do model selection. 13 -29

Using a validation set • Divide the total dataset into three subsets: – Training data is used for learning the parameters of the model. – Validation data is not used of learning but is used for deciding what type of model and what amount of regularization works best. – Test data is used to get a final, unbiased estimate of how well the networks. We expect this estimate to be worse than on the validation data. • We could then re-divide the total dataset to get another unbiased estimate of the true error rate. 13 -30

Early stopping • If we have lots of data and a big model, its very expensive to keep re-training it with different amounts of weight decay. • It is much cheaper to start with very small weights and let them grow until the performance on the validation set starts getting worse (but don’t get fooled by noise!) • The capacity of the model is limited because the weights have not had time to grow big. 13 -31

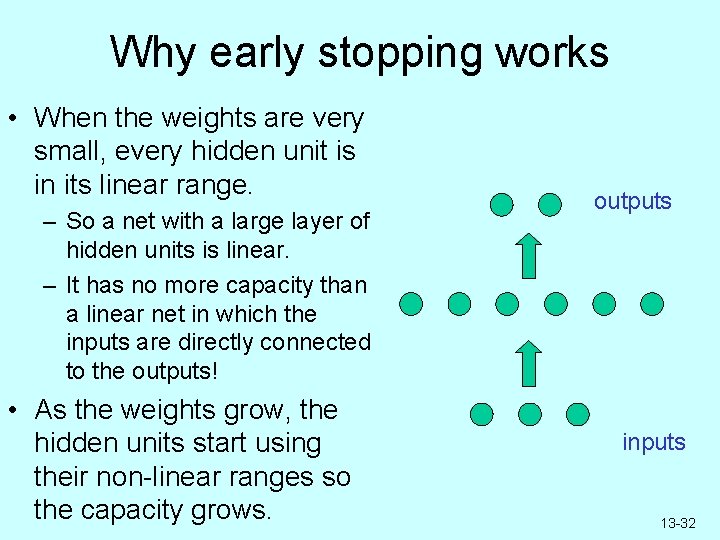
Why early stopping works • When the weights are very small, every hidden unit is in its linear range. – So a net with a large layer of hidden units is linear. – It has no more capacity than a linear net in which the inputs are directly connected to the outputs! • As the weights grow, the hidden units start using their non-linear ranges so the capacity grows. outputs inputs 13 -32

Model Assessment and Selection • • • Loss Function and Error Rate Bias, Variance and Model Complexity Optimization AIC (Akaike Information Criterion) BIC (Bayesian Information Criterion) MDL (Minimum Description Length) 13 -33

Key Methods to Estimate Prediction Error • Estimate Optimism, then add it to the training error rate. • AIC: choose the model with smallest AIC • BIC: choose the model with smallest BIC 13 -34

Model Assessment and Selection • Model Selection: – estimating the performance of different models in order to choose the best one. • Model Assessment: – having chosen the model, estimating the prediction error on new data. 13 -35

Approaches • data-rich: – data split: Train-Validation-Test – typical split: 50%-25% (how? ) • data-insufficient: – Analytical approaches: • AIC, BIC, MDL, SRM – efficient sample re-use approaches: • cross validation, bootstrapping 13 -36

Model Complexity 13 -37

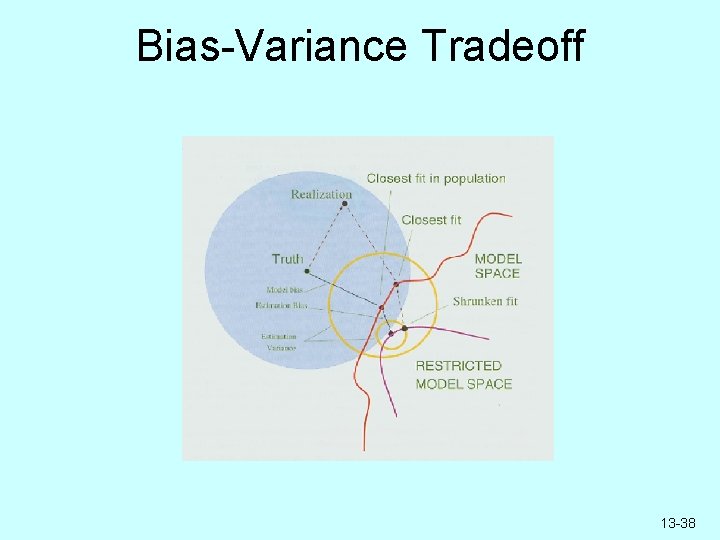
Bias-Variance Tradeoff 13 -38

Summary • Cross validation: A practical way to estimate model error. • Model Estimation should be done with a penalty • When best model estimation is chosen, estimate on whole data or average models on cross validated data 13 -39

Loss Functions • Continuous Response squared error absolute error • Categorical Response 0 -1 loss log-likelihood 13 -40

Error Functions • Training Error: – the average loss over the training sample. – Continuous Response: – Categorical Response: • Generalization Error: – the expected prediction error over an independent test sample. – Continuous Response: – Categorical Response: 13 -41

Detailed Decomposition for Linear Model Family • average squared bias decomposition =0 for LLSF; >0 for ridge regression trade off with variance; 13 -42