Model Predictive Control of a Powder Coating Curing







![First principle PDE model [Bombard et al, 2006] 2 λc, p ¶ Tp (z, First principle PDE model [Bombard et al, 2006] 2 λc, p ¶ Tp (z,](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-8.jpg)
![First principle PDE model [Bombard et al, 2006] 3 boundary conditions for the temperature: First principle PDE model [Bombard et al, 2006] 3 boundary conditions for the temperature:](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-9.jpg)
![First principle PDE model [Bombard et al, 2006] The degree of cure x(z, t) First principle PDE model [Bombard et al, 2006] The degree of cure x(z, t)](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-10.jpg)



![Model predictive control strategy [Dufour et al, IEEE TCST 11(5) 2003] • • Originaly Model predictive control strategy [Dufour et al, IEEE TCST 11(5) 2003] • • Originaly](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-14.jpg)








- Slides: 33

Model Predictive Control of a Powder Coating Curing Process: an Application of the MPC@CB© Software by: Kamel Abid, Pascal Dufour, Isabelle Bombard, Pierre Laurent CCC’ 07, Zhangjiajie, July, 27 -29 2007 Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 1

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 2

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 3

Control problem statement • Painting applications in: building (outdoor and indoor), furniture, cars accessories … • Need to decrease pollution due to the painting: organic solvent based coating are replaced by powder coatings • Quite recently, UV-curable powder coatings and lowtemperature coatings designed for heat sensitive substrates have appeared on the coatings market. • But few studies on curing kinetics, thermal modelling and control of such powder coating curing process: trajectory tracking or minimization of curing time or … Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 4

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 5

First principle PDE model Powder coatings = fine particles of: resin + cross-linker in thermosetting or thermoplastic powder coatings + pigments + extenders + flow additives and fillers to achieve specific properties (color, …. ) Schematic drawing of the “substrat+powder” sample Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 6

First principle PDE model 1. Thermal model based on the Fourier law of heat conduction uses: 1. the temperature variable varying in the thickness of the powder coated metal sample 2. the degree of cure conversion variable (ranging from 0+ to 1 at the end) 2. A non linear PDE Boundary control problem has to be tackled Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 7
![First principle PDE model Bombard et al 2006 2 λc p Tp z First principle PDE model [Bombard et al, 2006] 2 λc, p ¶ Tp (z,](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-8.jpg)
First principle PDE model [Bombard et al, 2006] 2 λc, p ¶ Tp (z, t) epΔH 0 ¶Tp (z, t) k 0 e = 2 ρp. Cpp ¶t ¶z ( -Ea ) RTp (z, t) m x (1 - x)n ] [ "z Î 0, ep , "t > 0 Tp(z, t) = temperature across the powder film thickness ep = film thickness (~0. 1 mm) x(z, t) = degree of cure λc, s ¶ 2 Ts (z, t) ¶ Ts (z, t) = 2 ρs Cps ¶t ¶z ] [ " z Î ep , ep + e s , " t > 0 Ts(z, t) = temperature across the substrate es = film thickness (~1 mm) Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 8
![First principle PDE model Bombard et al 2006 3 boundary conditions for the temperature First principle PDE model [Bombard et al, 2006] 3 boundary conditions for the temperature:](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-9.jpg)
First principle PDE model [Bombard et al, 2006] 3 boundary conditions for the temperature: - λp ¶Tp (z, t) ¶z 4 4 = αirφir (t) - σεp (Tp (z, t) - Text ) - hp (Tp (z, t) - Text ) Manipulated variable at z = 0, "t > 0 ¶Tp (z, t) at z = ep , "t > 0 - λc, p = -λc, s ¶z ¶z ¶Ts (z, t) 4 4 - λs = -σεs (Ts (z, t) - Text ) - hs (Ts (z, t) - Text ) ¶z at z = ep + es , "t > 0 Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 9
![First principle PDE model Bombard et al 2006 The degree of cure xz t First principle PDE model [Bombard et al, 2006] The degree of cure x(z, t)](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-10.jpg)
First principle PDE model [Bombard et al, 2006] The degree of cure x(z, t) of the powder: ¶x(z, t) = k 0 e ¶t ( -Ea ) RTp (z, t) m x (1 - x)n [ ] "z Î 0, ep , "t > 0 Initial conditions: Tp (z, t) = Ts (z, t) = Text"z Î [0, ep + es ], t = 0 x(z, t) = 0 + "z Î [0, ep ], t = 0 Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 10

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 11

Model predictive control strategy Advantages: - constraints (such as manipulated variables physical limitations, constraints due to operating procedures or safety reasons…) may be specified - a model aims to predict the future behavior of the process and the best one is chosen by a correct optimal control of the manipulated variables. Drawbacks: - computational time needed may limit online use - suboptimal solutions - how to handle unfeasibilities Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 12

Model predictive control strategy j=k +Np ì ïmin J(u) f(yref (j), yp (j) = ï u j=k +1 ï ïsubject to constraints on the manipulated variable : ï íumin £ u(j) £ umax"j Î {k + 1, k + Np} ï ïΔumin £ u(j) - u(j - 1) £ Δumax"j Î {k + 1, k + Np} ï ïsubject to constraints on the controlled variable : ïc(y (j), y (j)) £ 0"j Î {k + 1, k + Np} ref î p å[ ] The function f means: trajectory tracking, processing time minimization, productivity function … Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 13
![Model predictive control strategy Dufour et al IEEE TCST 115 2003 Originaly Model predictive control strategy [Dufour et al, IEEE TCST 11(5) 2003] • • Originaly](https://slidetodoc.com/presentation_image_h2/5bd05461ddb6e4b85688ec034ec34195/image-14.jpg)
Model predictive control strategy [Dufour et al, IEEE TCST 11(5) 2003] • • Originaly developed for nonlinear PDE model control Main idea: decrease the online time needed to compute the PDE model based control Approach: • Input constraints: hyperbolic transformation • Output constraints: exterior penalty method • Linearization + sensitivites computed off line • On line use of a time varying linear model • On line resolution of a penalized (and so unconstrained) optimization control problem : a modified Levenberg Marquardt Algorithm Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 14

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 15

MPC@CB© software main features 1. 2. 3. 4. Developed under Matlab, MPC@CB© solves any user defined : § trajectory tracking problem § operating time minimization problem § any cost function § input/output constraint handled Any user defined continuous model (SISO, MISO, SIMO, MIMO model), including large scale PDE model Easy to introduce a user defined observer Easy to apply the software for simulation or real time application MPC@CB ©: flexibility/ease for a quick use in control ! Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 16

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 17

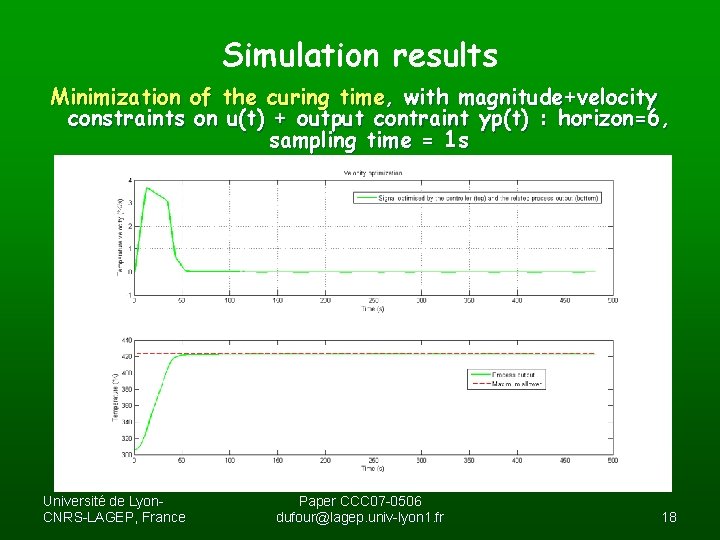
Simulation results Minimization of the curing time, with magnitude+velocity constraints on u(t) + output contraint yp(t) : horizon=6, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 18

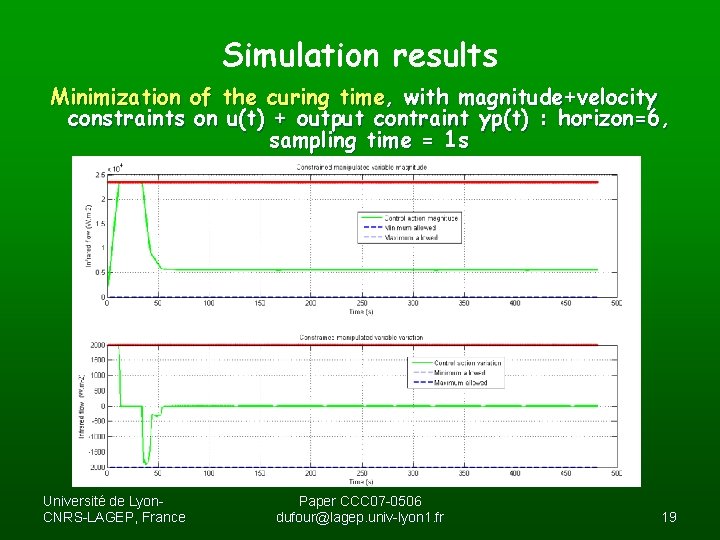
Simulation results Minimization of the curing time, with magnitude+velocity constraints on u(t) + output contraint yp(t) : horizon=6, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 19

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 20

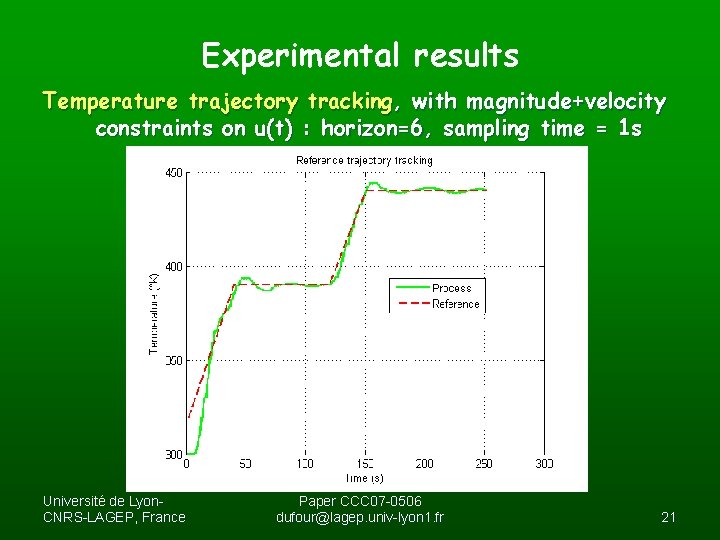
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=6, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 21

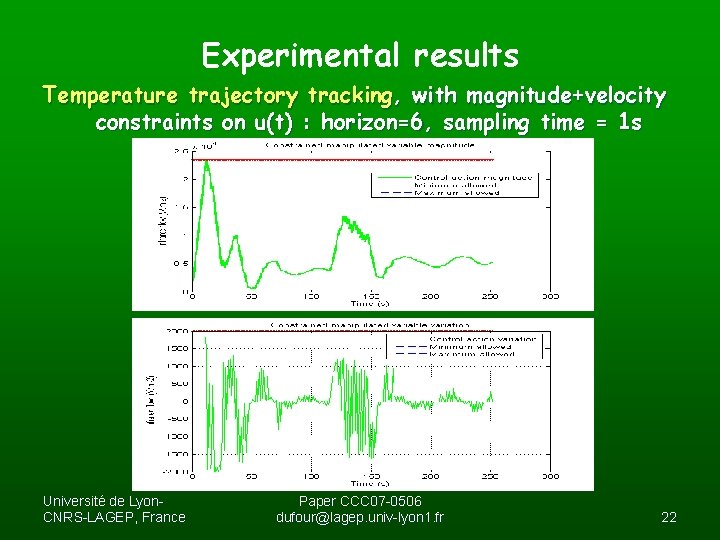
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=6, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 22

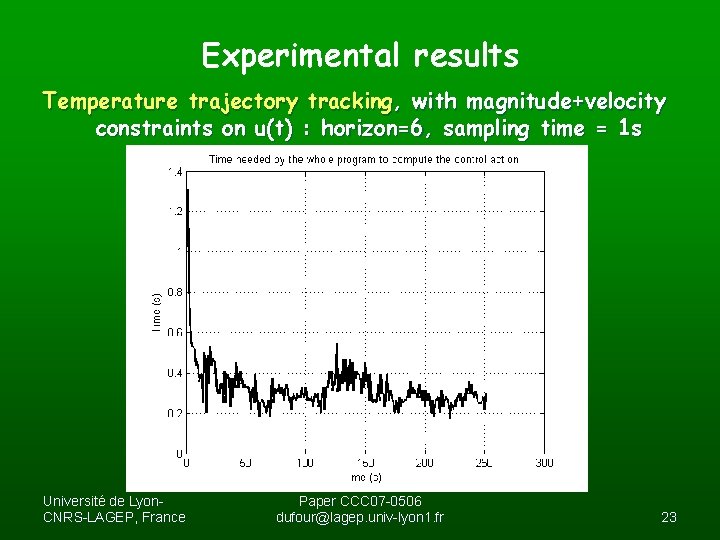
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=6, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 23

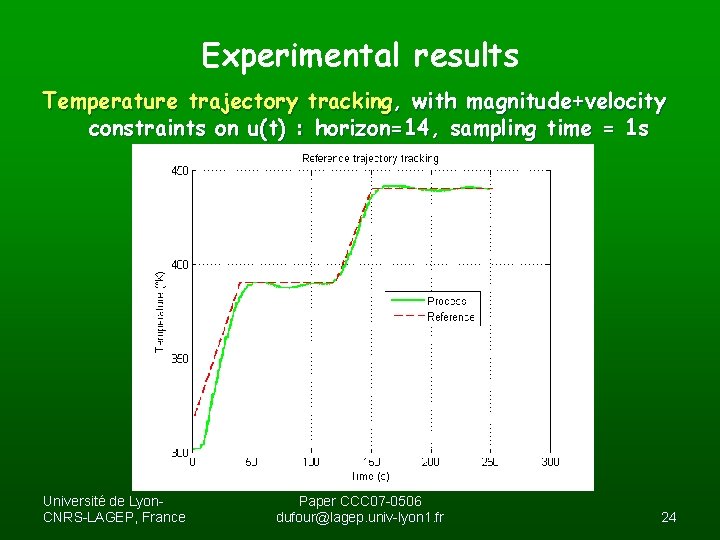
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=14, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 24

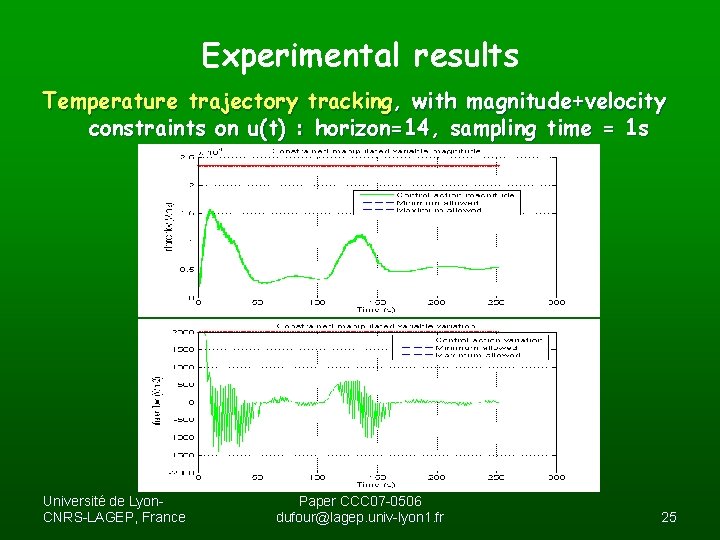
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=14, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 25

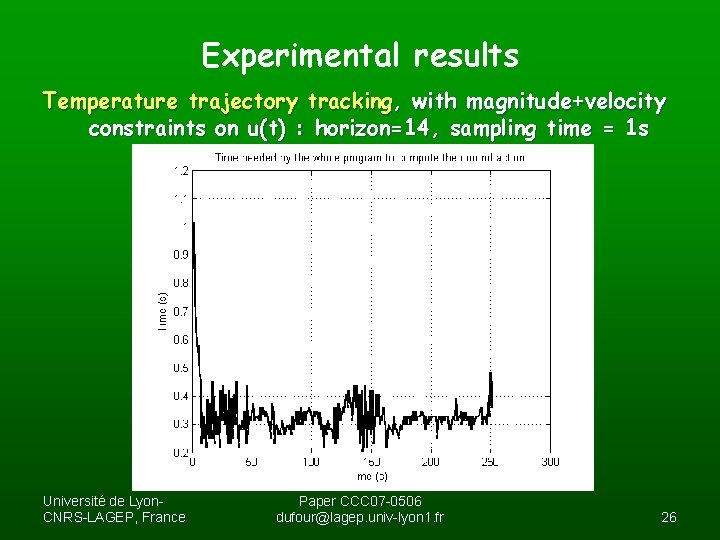
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=14, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 26

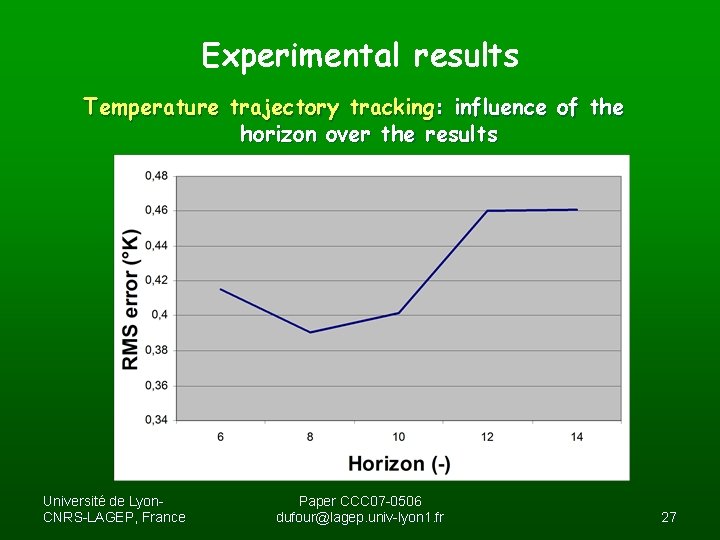
Experimental results Temperature trajectory tracking: influence of the horizon over the results Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 27

Outline 1. Control problem statement 2. First principle PDE model 3. Model predictive control strategy 4. MPC@CB© software main features 5. Simulation results 6. Experimental results 7. Conclusions & perspectives Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 28

Conclusions • • The real time control of powder curing is possible : temperature trajectory tracking Experimental control of PDE system by a general MPC@CB© software has been shown Perspectives • • • Minimization of the powder curing time under constraints: an observer is under development MPC@CB© may be used for any process: since its development, it is currently used for control of polymer production, vial lyophilisation, pasta drying. To use MPC@CB©: dufour@lagep. univ-lyon 1. fr Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 29

Thank you Any questions ? Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 30

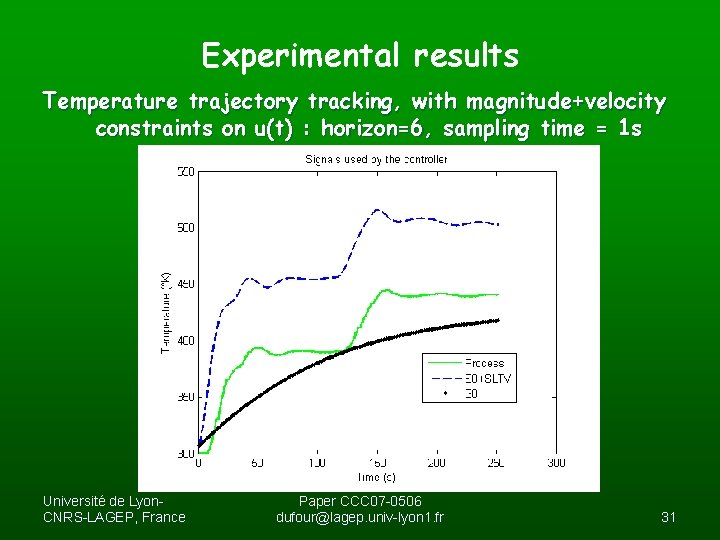
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=6, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 31

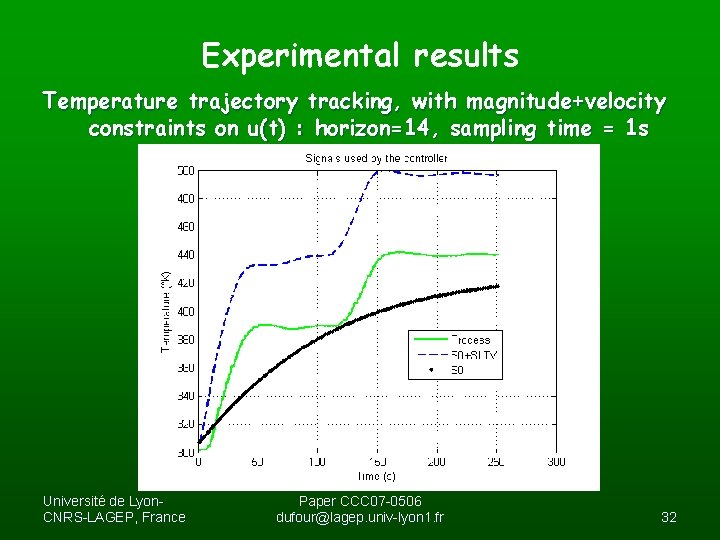
Experimental results Temperature trajectory tracking, with magnitude+velocity constraints on u(t) : horizon=14, sampling time = 1 s Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 32

Université de Lyon. CNRS-LAGEP, France Paper CCC 07 -0506 dufour@lagep. univ-lyon 1. fr 33