Model matematik trafik n n Proses kelahiran proses

Model matematik trafik n n Proses kelahiran proses datangnya panggilan Proses Kematian proses berakhirnya panggilan Kondisi/keadaan menyatakan banyaknya saluran yang diduduki. Probabilitas kondisi lamanya suatu kondisi diduduki dalam selang waktu 1 jam.

Diagram Kondisi n n Dinyatakan dengan lingkaran yang diberi angka. Angka menunjukkan jumlah saluran yang diduduki 0 0 1 1 2 2 3 3 3 saluran diduduki

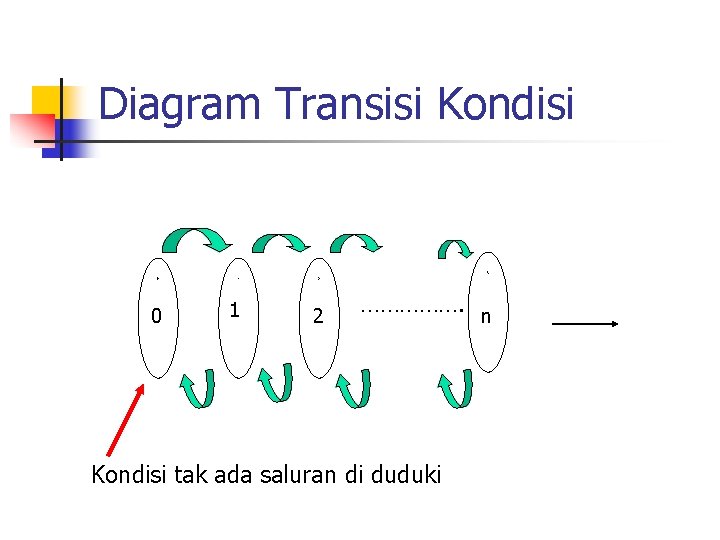
Diagram Transisi Kondisi 3 0 0 1 1 2 2 ……………. n Kondisi tak ada saluran di duduki

Persamaan kondisi n n n Probabilitas datangnya satu panggilan pd kondisi n dalam waktu dt : bn dt Probabilitas berakhirnya satu panggilan pd kindisi n dalam waktu dt : dn dt Probabilitas terjadinya lebih dari satu peristiwa = 0

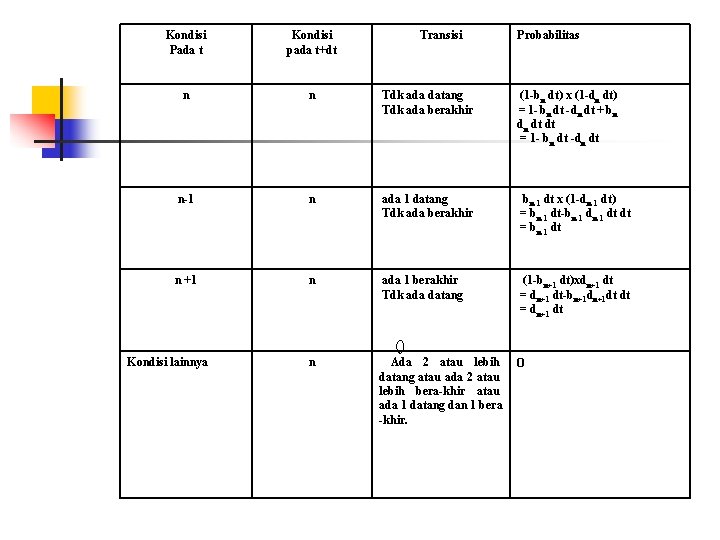
Kondisi Pada t Kondisi pada t+dt n n Tdk ada datang Tdk ada berakhir (1 -bn dt) x (1 -dn dt) = 1 - bn dt - dn dt + bn dn dt dt = 1 - bn dt -dn dt n-1 n ada 1 datang Tdk ada berakhir bn-1 dt x (1 -dn-1 dt) = bn-1 dt-bn-1 dt dt = bn-1 dt n +1 n ada 1 berakhir Tdk ada datang (1 -bn+1 dt)xdn+1 dt = dn+1 dt-bn+1 dt dt = dn+1 dt n Ada 2 atau lebih datang atau ada 2 atau lebih bera-khir atau ada 1 datang dan 1 bera -khir. 0 Kondisi lainnya Transisi Probabilitas

Persamaan kondisi P(n, t+dt) = P(n, t)x[1 -bn dt – dn dt] & berakhir + P(n-1, t)x[bn-1 dt] 1 datang + P(n+1, t)x[dn+1 dt] 1 berakhir +0 lainnya = P(n, t) – P(n, t)[ bn dt + dn dt] + P(n-1, t)[bn-1 dt] + P(n+1, t)( dn+1 dt) P(n, t+dt)- P(n, t) = - P(n, t)[ bn dt+dn dt] + P(n-1, t)[bn-1 dt] + P(n+1, t)( dn+1 dt) dp (n, t) dp(n, t)= -P(n, t)[bndt+dndt]+P(n-1, t)bn-1 dt+P(n+1, t)dn+1 dt dp(n, t)= -P(n, t)[bn+dn]+P(n-1, t)bn-1+P(n+1, t)dn+1 dt Kondisi kesetimbangan : dp(n, t) = 0 dt 0 = -P(n, t)[bn+dn]+P(n-1, t)bn-1+P(n+1, t)dn+1 0 = -P(n)[bn+dn]+P(n-1)bn-1+P(n+1)dn+1 P(n)( bn+dn) = P(n-1)bn-1+P(n+1)dn+1 pers kondisi

Kesetimbangan n=0: P(0)(b 0 + d 0) = P(-1)b-1 + P(1) d 1 P (0)b 0 = P(1) d 1 n=1 P(1)(b 1 + d 1) = P(0)b 0 + P(2) d 2 P(1)(b 1 + d 1) = P(1)d 1 + P(2) d 2 P(1)b 1 = P(2) d 2 n=2 P(2)(b 2 + d 2) = P(1)b 1 + P(3) d 3 P(2)(b 2 + d 2) = P(2)d 2 + P(3) d 3 P(2)b 2 = P(3) d 3 n=n P(n)bn = P(n+1)dn+1 pers kesetimbangan

Probablts datang panggilan = Probabltas berakhirnya panggilan dp(n, t)= -P(n, t)[bn+dn]+P(n-1, t)bn-1+P(n+1, t)dn+1 dt pada n=0 dp(0, t)= -P(0, t)[b 0+d 0]+P(-1, t)b-1+P(1, t)d 1 dt = -P(0, t)b 0+P(1, t)d 1 Jika hanya ada panggilan datang saja dengan -b 0 = b 1 = b 2 = … = a dn = 0 maka dp(0, t)= -a. P(0, t)

pada n=1 dp(1, t)= -P(1, t)[b 1+d 1]+P(0, t)b 0+P(2, t)d 2 dt = -P(1, t). a + P(0, t)a = a P(0, t) - a. P(1, t) pada n=n dp(n, t)= -P(n, t)[bn+dn]+P(n-1, t)bn-1+P(n+1, t)dn+1 dt = -P(n, t). bn + P(n-1, t) bn-1 = -a P(n, t) + a. P(n-1, t)

Solusi persamaan Deferensial Untuk n = 0 P(0, t) = e-at Untuk n =1 P(1, t)= a. P(0, t)-a P(1, t) dt = a e-at - a. P(1, t) = a t e-at n=n P (n, t) = (at)n e-at Distribusi Poisson n!

Distribusi Poisson Berlaku untuk : n Sumber panggilan jumlahnya tak hingga n Jumlah saluran yang disediakan tak hingga n Rate kedatangan random

Distribusi Poisson σ

Mean = Varian M = s 2 Jika : n S = ~ , N = ~ distribusi Poisson n S = ~ , N = terbatas distribusi Erlang n S = terbatas , N = terbatas distribusi binomial n S = terbatas, N = terbatas dan S > N Engset n

Distribusi Poison : n n n Berlaku untuk : - kedatangan acak dengan rate tetap. Jumlah sumber = Tak hingga Jumlah kanal / saluran = Tak hingga Mean = Variansi Distribusi tersebut diperoleh untuk nilai koefisien kela-hiran yang tetap untuk semua kondisi yaitu a bo = b 1 = b 2 = ……. . bn = a

Persamaan Poisson P(n) = ( An / n ! ) x e-A. n N= jumlah saluran/jumlah panggilan n A = Intensitas trafik=Mean

Contoh n 1. 2. 3. 4. Rata-rata panggilan datang setiap 5 detik terjadi selama periode 10 detik, tentukan probabilitas: Tak ada panggilan datang? Satu panggilan datang? Dua panggilan datang? Lebih dari 2 panggilan datang?

Jawab P(n) = ( An / n ! ) x e-A. A = 2, 1. P(0) = 0, 135 2. P(1) = 0, 270 3. P(2) = 0, 270 4. P(>2) =1 -P(0)-P(1)-P(2)=0, 325

“ DISTRIBUSI ERLANG”. n Berlaku u/ sumber panggilan tak hingga ttp CH terbatas. S=~ N = terbatas.

a 0 a 1 a 2 2 a 3 3 a ………… N 4 N

n Dari distribusi Poisson P(n) = ( An / n ! ) x e-A Probabilitas total = 1. Maka : = P(0) + P(1) + P(2) + ………. + P(N). = P(0) + AP(0) + (A 2/2!). P(0) + ……. + (AN/N!). P(0). = P(0) x { 1 + A + (A 2/2!) + ……. + (AN/N!) }. 1 = P(0) x Ai / i!.

P(0) = 1 N Ai / i!. i=0 . N P(n) = ( An / n! ) x [ 1 / ( Ai / i! ) ] i=0 = An / n! 1 + A + (A 2/2) + A 3/3!) + …. (AN / N!). P (n) = An / n!. N Ai / i!. i=0 = B = GOS = Prob. Blocking. .

Contoh 1 N = 3 , Intensitas (A) = 3. GOS = P(3) = ( 33 / 3 ! ) = ( 27/6 ). 1+3+(32/2) + (33/3!) 1 + 3 + 4, 5 + (27/6) = ( 4, 5 / 13 ) = 0, 34 = 34 %.

Contoh n Diketahui suatu sentral memiliki 6 saluran (kanal), trafik yang ditawarkan adalah 4 Erlang (A). Berapa Grade Of Service (GOS) dr sentral tersebut ?

Jawab GOS= P(6)= An/n! = 46/6 !. N 6 Ai / i!. 46 / 6! i=0 ( 4096/720). = 1+A+A 2/2+A 3/3!+A 4/4!+A 5/5!+A 6/6! = ( 4096 / 720 ). 1+4+16/2+64/6+256/24+1024/120+ 4096/720 GOS = 0, 117 12 %.