MODEL ENTITETIODNOSI ER ENTITYRELATIONSHIP MODEL Peter Chen 1976

MODEL ENTITETI-ODNOSI E-R (ENTITY-RELATIONSHIP) MODEL Peter Chen 1976 g.

Osnovni pojmovi o modelu podataka • Skup konceptualnih i logičkih sredstava, stavljenih na raspolaganje projektantu baze, radi opisivanja podataka, njihovih odnosa, integritetskih ograničenja, kao i apstraktnih operacija u cilju postavljanja upita bazi, naziva se model podataka.

Model podataka treba da sadrži tri ključna elementa: • Jedinstven način grafičkog predstavljanja sadržaja baze- konceptualno predstavljanje ; • Jasno definisane osnovne informacione strukture modela (nosioce podataka)logičko predstavljanje; • Jasno definisane apstraktne operatore modela koji služe za postavljanje upita bazi.

Entiteti i skupovi entiteta • Entitet je svaki objekat koji se može razlikovati od svih ostalih objekata u nekom univerzumu, što znači da se može jednoznačno identifikovati. (Npr. čovjek, knjiga, istorijska kategorija, društveno uređenje, dio neke misaone klasifikacije. . . ) • Grupa entiteta istog tipa naziva se skup entiteta. (Npr. skup studenata univerziteta) • Skupovi entiteta imaju pridružena neka svojstva ili atribute putem kojih se može testirati da li neki entitet pripada datom skupu entiteta. • Skupovi entiteta ne moraju biti potpuno razdvojeni u smislu njihovih svojstava. (Npr. zaposleni i čovjek )

Atributi • Atributi su svojstva entiteta i njihovih skupova. • Npr. skup entiteta zaposleni može da ima atribute: IME, PREZIME, BRLK, STAŽ. • Za svaki atribut postoji skup dozvoljenih vrijednosti koji se naziva domenom atributa. • Formalno gledano atribut predstavlja funkciju Aj koja preslikava skup entiteta Ei u odgovarajući domen Dj : Aj: Ei -> Dj Aj(ek) = vi, gdje je ek Ei, a vi Dj

Primjer • Ako je ek entitet iz skupa entiteta zaposleni, tj. ek=<‘Petar Petrović’, ‘ 11123’, 15> tada možemo pisati: IME (ek) = ‘Petar Petrović’ BRLK (ek) = ‘ 11123’ STAŽ (ek) = 15 • Napomenimo da se iz ove definicije da zaključiti da svaki atribut sadrži atomsku vrijednost.

Odnosi i skupovi odnosa • Odnos je neka vrsta asocijacije ili veze između dva ili više entiteta. Pritom, entiteti ne moraju pripadati različitim skupovima entiteta. Npr. odnos otac-sin definiše odnos između dva entiteta istog skupa čovjek. • Pod skupom odnosa podrazumijevamo više odnosa istog tipa.

Formalna definicija skupa odnosa • Skup odnosa je matematička relacija nad dva ili više skupova entiteta, gdje skupovi entiteta ne moraju biti različiti. Drugim riječima, skup odnosa R jeste podskup Dekartovog proizvoda skupova entiteta, tj. R = {<ei 1, ei 2, . . . eik> ei 1 Ej 1, . . . , eik Ejk } gdje su ei 1, . . . , eik pojedinačni entiteti, a Ej 1, . . . , Ejk odgovarajući skupovi entiteta. Primjer: R = {<ei 1, ei 2> ei 1 čovjek, ei 2 čovjek }

Skupovi odnosa • Putem E-R modela najlakše se izražavaju binarni odnosi, dok se proizvoljni n-arni odnosi teže izražavaju. • Kao i skupovi entiteta tako i skupovi odnosa mogu imati svoje atribute. Npr. atribut skupa odnosa student-predmet može biti OCJENA. • Uloge : student polaže predmet slušaju studenti

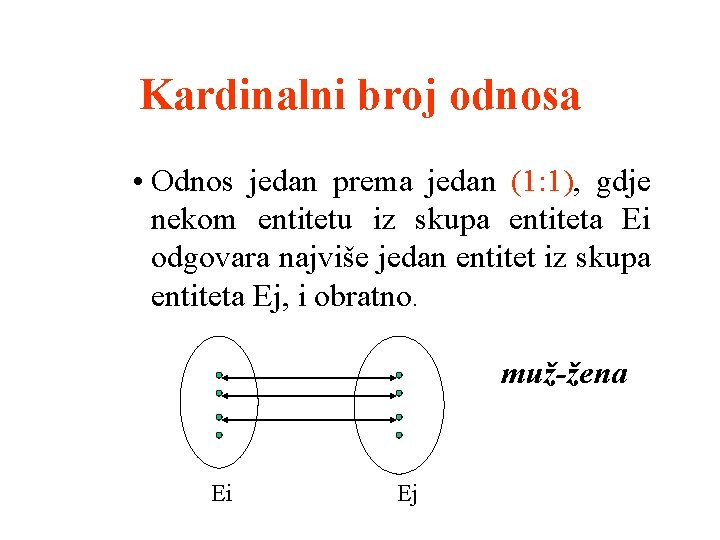
Kardinalni broj odnosa • Odnos jedan prema jedan (1: 1), gdje nekom entitetu iz skupa entiteta Ei odgovara najviše jedan entitet iz skupa entiteta Ej, i obratno. muž-žena Ei Ej

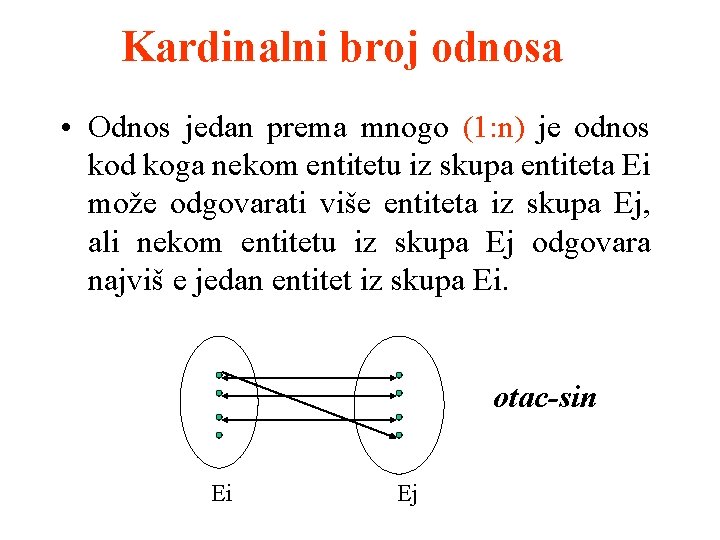
Kardinalni broj odnosa • Odnos jedan prema mnogo (1: n) je odnos kod koga nekom entitetu iz skupa entiteta Ei može odgovarati više entiteta iz skupa Ej, ali nekom entitetu iz skupa Ej odgovara najviš e jedan entitet iz skupa Ei. otac-sin Ei Ej

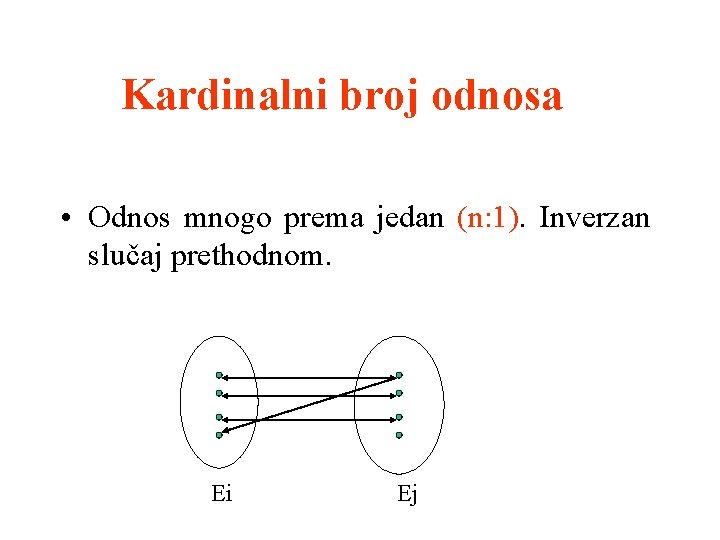
Kardinalni broj odnosa • Odnos mnogo prema jedan (n: 1). Inverzan slučaj prethodnom. Ei Ej

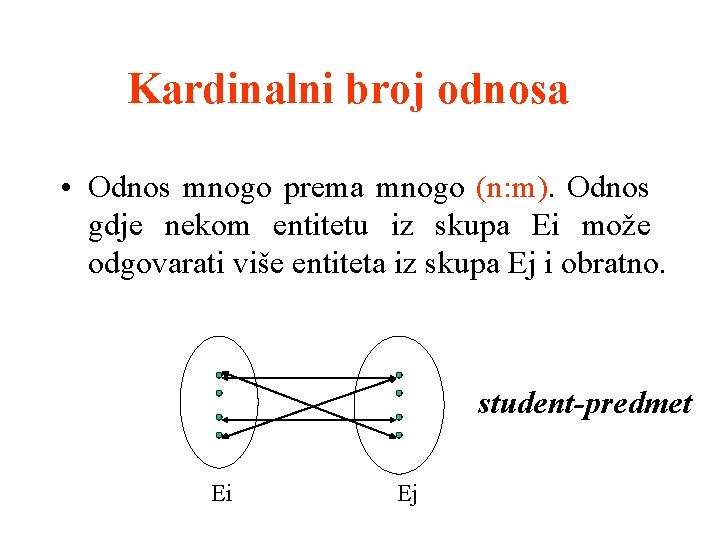
Kardinalni broj odnosa • Odnos mnogo prema mnogo (n: m). Odnos gdje nekom entitetu iz skupa Ei može odgovarati više entiteta iz skupa Ej i obratno. student-predmet Ei Ej

Kardinalni broj odnosa Greške projektanta prilikom specificiranja kardinalnog broja mogu dovesti do: 1. povećanja dupliciranosti podataka i nepotrebnog uslovljavanja 2. nametanja ograničenja koja ne odgovaraju stvarnosti a time i nemogućnosti predstavljanja određene informacije.

Egzistencijalna zavisnost Ako postojanje nekog entiteta X u bazi zavisi od prisutnosti nekog entiteta Y u bazi, onda kažemo da je X egzistencijalno zavisan od Y. U operacionom smislu to znači da ako se izbriše Y iz baze onda se mora izbrisati i X. U ovakvom odnosu entitet Y je dominantni entitet a X podređeni entitet. Po istom principu imamo dominantne i podređene skupove entiteta.

Egzistencijalna zavisnost • Npr. u nekom preduzeću se vodi evidencija o izdržavanim članovima porodice zaposlenih u tom preduzeću. Pritom ako izbrišemo zaposlenog onda moramo izbrisati i članove njegove porodice.

Primarni ključ- nadključ Podskup atributa putem koga se jednoznačno mogu odrediti entiteti u skupu entiteta naziva se nadključ (super ključ) tog skupa entiteta. Pr: zaposleni (IME, BRLK, STAŽ) • BRLK • IME ako sa sigurnošću možemo tvrditi da svi zaposleni imaju različita imena.

Nadključ Formalno gledano nadključ se može definisati kao grupa atributa datog skupa entiteta koja omogućava jednoznačno preslikavanje entiteta iz datog skupa na Dekartov proizvod domena tih atributa, tj. NK(Ei) = ( Ai 1, Ai 2, . . . Aik )=fi : Ei ->Di 1 Di 2. . . Dik

Nadključ Sam pojam nadključa ne podrazumijeva minimalnost broja atributa koji ga specificiraju. Pr: zaposleni (IME, BRLK, STAŽ) • BRLK NK(zaposleni) • BRLK, IME NK(zaposleni) • Ako je X nadključ onda je i svaki nadskup atributa iz X, tj. skup atributa koji kao pravi podskup sadrži X, takođe nadključ.

Kandidatski ključ Koncept nadključa nije dovoljan za naše potrebe. Nas interesuje onaj najmanji nadključ koji ne sadrži suvišne atribute. Takav nadključ naziva se kandidatski ključ. Prema tome, kandidatski ključ K jeste skup atributa koji: 1. omogućava jednoznačno preslikavanje sa skupa entiteta na Dekartov proizvod domena tih atributa, tj. za sve ei, ej Ei, K(ei) K(ej) 2. nijedan pravi podskup tog skupa atributa koje sačinjavaju kandidatski ključ nema tu osobinu, tj. ako je K K onda postoje ei, ej Ei, takvi da K (ei) = K (ej)

Primarni ključ Pr: zaposleni (IME, BRLK, STAŽ) • BRLK • IME KK(zaposleni) PK Međutim, nas interesuje samo jedan od mogućih kandidatskih ključeva koji bi služio kao primarni ključ za dati skup entiteta. Iz više kandidatskih ključeva za dati skup entiteta projektant baze podataka bira onaj koji je po svojoj semantici, udobnosti ili sasvim proizvoljno bolji da bude primarni ključ.

Primarni ključ nekog skupa entiteta Ei , u oznaci PK(Ei), jeste kandidatski ključ koji administrator baze podataka po svojoj volji izabrao kao glavno sredstvo za jednoznačno identifikovanje entiteta u tom skupu. Pr: PK(zaposleni)= BRLK

Jaki i slabi skupovi • Kod nekih skupova entiteta ne postoji dovoljan broj atributa koji bi mogli da sačinjavaju primarni ključ. Takvi skupovi se nazivaju slabi skupovi entiteta. • Jaki skupovi entiteta su oni koji imaju primarni ključ. Pr: zaposleni (BRLK, IME, STAŽ)- jaki (dominantni) skup izdržavani (IME_I, STAROST)- slabi (podređeni) skup

Jaki i slabi skupovikardinalnost Odnos između dominantnog i podređenog (jakog i slabog) skupa mora biti 1: 1 ili 1: n

PK slabog skupa • Uzimamo primarni ključ dominantnog skupa i njemu dodajemo potrebne atribute iz slabog skupa. Tako oformljeni skup atributa predstavlja primarni ključ slabog skupa. Ovaj dodatni skup atributa slabog skupa entiteta se naziva diskriminator slabog skupa. • Pr: zaposleni (BRLK, IME, STAŽ) izdržavani (IME_I, STAROST) PK(izdržavani )= BRLK, IME_I BRLK - PK(zaposleni ) IME_I - diskriminator

PK skupa odnosa I skupovi odnosa imaju svoje primarne ključeve. Po definiciji primarni ključ skupa odnosa jeste unija primarnih ključeva svih skupova entiteta koji ulaze u taj odnos, tj. : PK(R) = PK(Ei), gdje je Ei R

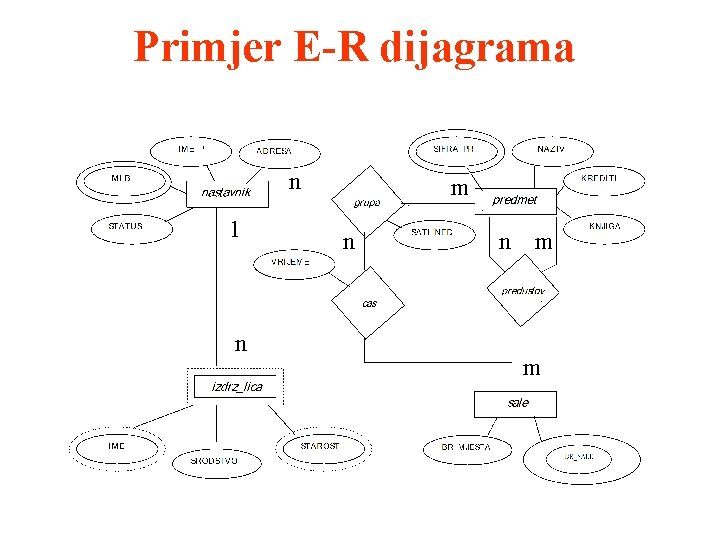
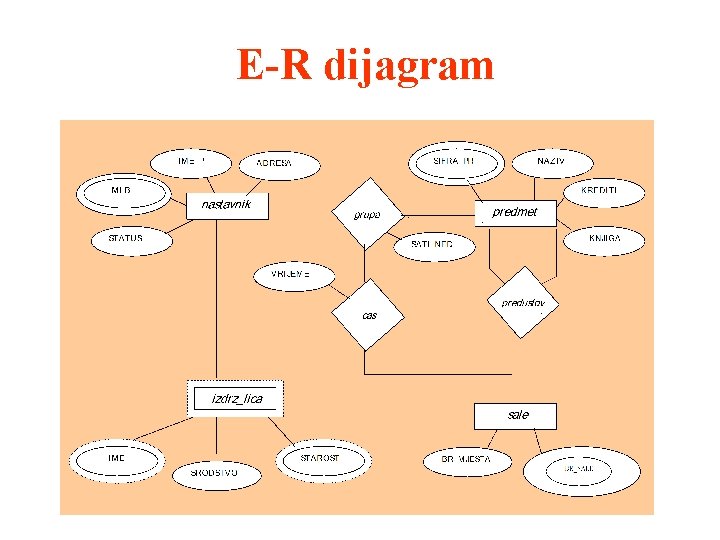
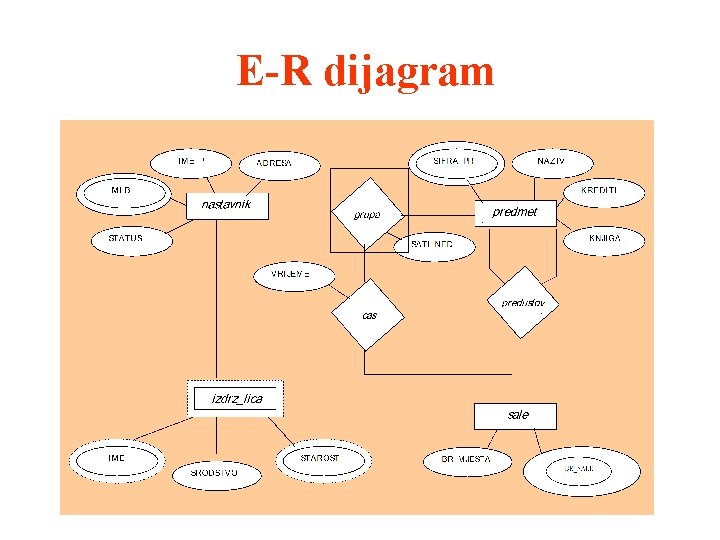
Dijagrami E-R modela Čitava konceptualna (logička) baza može se predstaviti putem dijagrama koji se sastoje od : 1. pravougaonika koji predstavljaju skupove entiteta 2. elipsi koje predstavljaju atribute 3. rombova koji predstavljaju skupove odnosa 4. linija koje povezuju odgovarajuće atribute, skupove entiteta i odnosa

Primjer E-R dijagrama n 1 n m n n m m

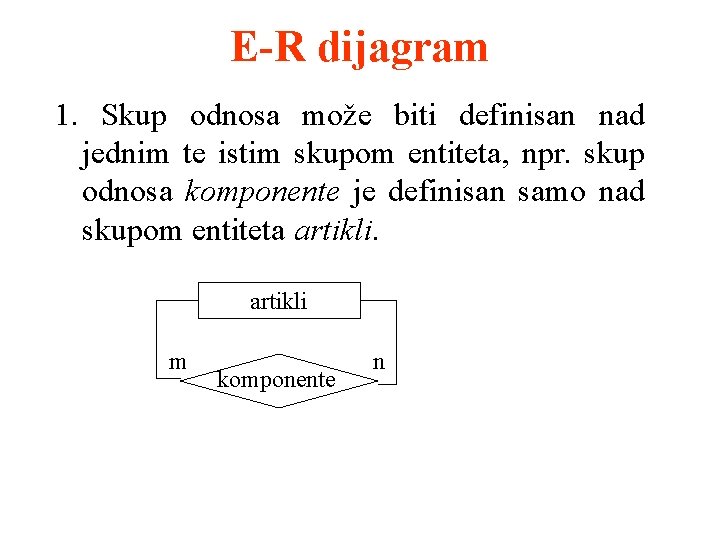
E-R dijagram 1. Skup odnosa može biti definisan nad jednim te istim skupom entiteta, npr. skup odnosa komponente je definisan samo nad skupom entiteta artikli m komponente n

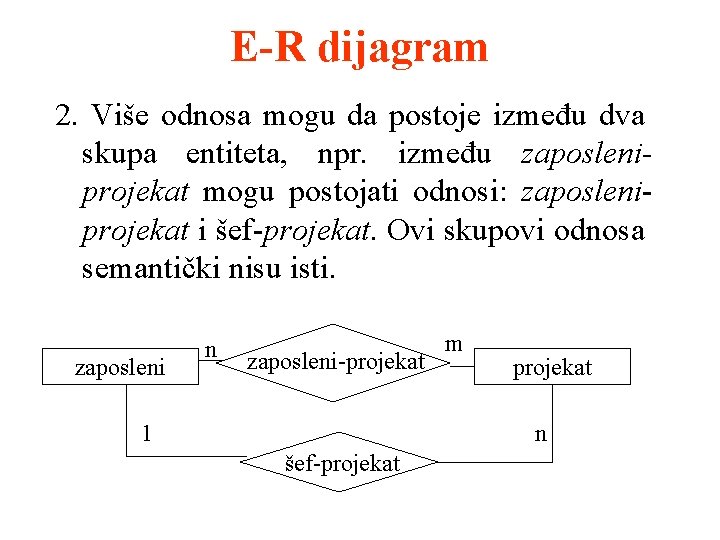
E-R dijagram 2. Više odnosa mogu da postoje između dva skupa entiteta, npr. između zaposleniprojekat mogu postojati odnosi: zaposleniprojekat i šef-projekat. Ovi skupovi odnosa semantički nisu isti. zaposleni n zaposleni-projekat 1 m projekat n šef-projekat

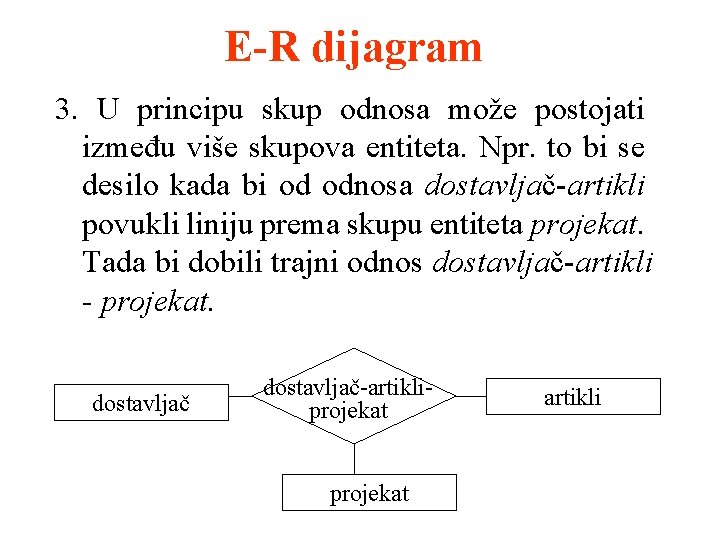
E-R dijagram 3. U principu skup odnosa može postojati između više skupova entiteta. Npr. to bi se desilo kada bi od odnosa dostavljač-artikli povukli liniju prema skupu entiteta projekat. Tada bi dobili trajni odnos dostavljač-artikli - projekat. dostavljač-artikliprojekat artikli

E-R dijagram 4. Putem E-R dijagrama može se na jednostavan način uočiti koji su jaki a koji slabi skupovi entiteta. 5. Jednoznačno se mogu uočiti ključevi skupova entiteta a samim tim i ključevi skupova odnosa.

E-R dijagram 6. U principu skupovi odnosa mogu povezivati ne samo skupove entiteta već i same skupove odnosa. To bi se desilo kada bi od odnosa dostavljač-artikli povukli liniju prema odnosu projekat-artikli. 7. Mogu se specificirati domeni atributa.

Integritetska ograničenja To su uslovi koje podaci moraju da zadovoljavaju da bi baza podataka bila konzistentna (tj. odgovarala realnom stanju sistema). Mogu biti prosta i strukturna (referencijalna)

Integritetska ograničenja E-R modela Prosta ograničenja: -domenska ograničenja (STAROST 1 -100, semestar I-IV, CIJENA realan broj, IME tekst dužine najviše 60, …) -primarni ključevi (različita pojavljivanja istog objekta moraju se jednoznačno identifikovati)

Integritetska ograničenja E-R modela Strukturna (referencijalna) ograničenja: - egzistencijalna zavisnost (postojanje podređenog objekta zavisi od postojanja dominantnog) - kardinalnost (broj pojavljivanja nekog objekta u bazi zavisi od kardinalnog broja)