Model Checking for CTL Marks the states of







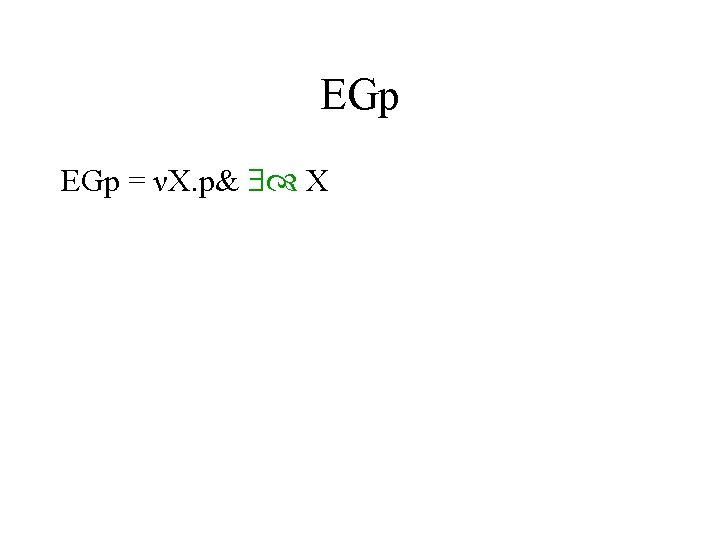




- Slides: 12

Model Checking for CTL Marks the states of K by subformulas of P s is marked by a subformula Q if Q holds at TK, s The algorithm proceeds from simple formulas to more complex formulas for all states simultaneously.

Algorithm For atomic formulas – immediately For Boolean connectives – easy s is marked by P 1& P 2 if …. For modal connectives: P 1 U P 2 : if from s there is a P 1 path to a P 2 node. For modal connectives: P 1 U P 2 ……

CTL* Modalities: E( a formula of TL(U)) A ( a formula of TL(U)) Semantics: T, s|= E C if there is a path from s which has a property C.

Model Checking for CTL* How to check E (‘ property of a path’) Construct an automaton A for the property. Take the product with the Kripke Structure.

Equation for P 1 U P 2 X - the set that satisfy P 1 U P 2 X= P 2 (X& P 1 ) X=H(X) where H = λ Y. P 2 (Y & P 1 ) How many solution Z=H(Z) has?

Characterization of P 1 U P 2 is the minimal solution of Z= P 2 (Z & P 1 ) X 0= P 2 Xn+1= P 2 (Xn & P 1 ) s in Xn iff there is a P 1 path of length≤ n+1 from s to P 2 X= Xn X=H(X) and H monotonic

Mu-calculus E : = At| ¬ At| X| E 1 &E 2| E 1 E 2| E | A E| μ X. E| νX. E Semantics: μ least fixed point; ν greatest fixed point. [| E |]ρ the set of states that satisfies E in the enviroment ρ: Var-> States.
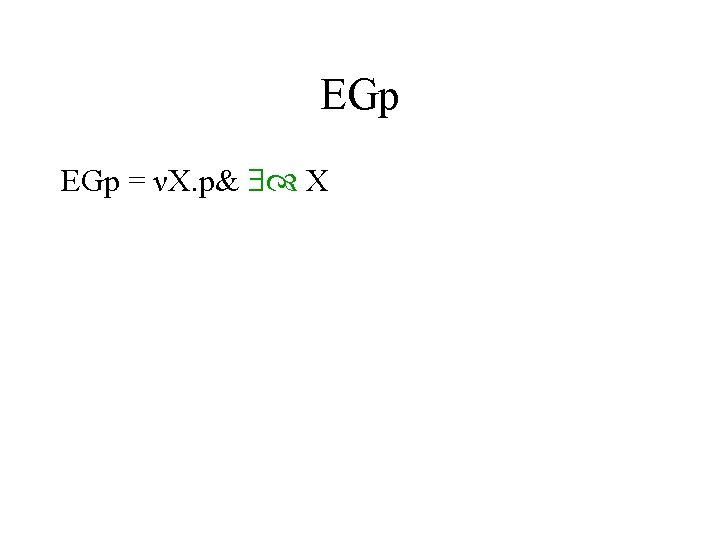
EGp = νX. p& X

From mu-calculus to MLO Theorem: for every mu-formula c(X 1, …, Xn) there is an MLO formula b(t, X 1, …Xn) which is equivalent to c over trees. Theorem: for every future MLO formula b(t, X 1, …Xn) which is invariant under counting there is an equivalent (over trees) mu formula c.

Symbolic Model Checking Explicit Model Checking: Input a finite state K and a formula c Task Find the states of K that satisfy c. Symbolic model checking Input a description of K and a formula c Task Find a description of the states of K that satisfy c.

A description of Kripke structures by formulas • s(x 1, …, xn) describes a set of states • t(x 1, …xn, x 1’, …xn’) describes transitions • For every label p a formula lp(x 1, …xn) that describes the states labeled by p.

BDT, and OBDD • Binary decision trees • Ordered Binary Decision Diagrams.