Model checking and refinement checking for modal transition

Model checking and refinement checking for modal transition systems and their cousins MTS meeting 2007 Adam Antonik & Michael Huth imperial. ac. uk/quads Page 1 © Imperial College London

PART 1 REPORT ON PUBLISHED WORK ON MODEL CHECKING PARTIAL KRIPKE STRUCTURES 2 © Imperial College London

Partial Kripke structures • Often need aggressive abstraction of model prior to model checking • Partial state spaces facilitate this, as Kripke structures with 3 -valued labeling [Bruns & Godefroid 1999] 3 © Imperial College London

Abstraction-based model checking • Partial Kripke structures have abstraction & refinement notion • System = Kripke structure • Abstraction = Partial Kripke structure, refined by System • Verification Problem: “Do all Kripke structure refinements of Abstraction satisfy formula of mu -calculus? ” - If so, System will satisfy it, too. - If not, we may be no wiser. 4 © Imperial College London

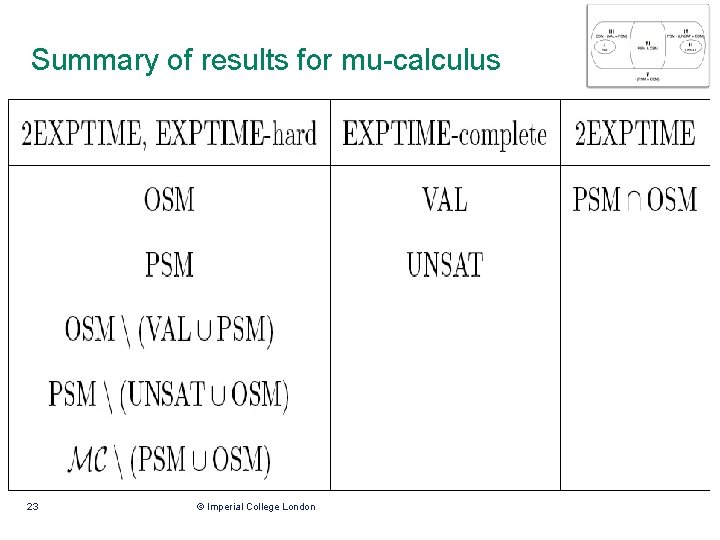
Complexity, Soundness & Incompleteness • Verification Problem: “Do all Kripke structure refinements of Abstraction satisfy formula of mucalculus? ” • This is EXPTIME-complete in formula, quadratic in model [Bruns & Godefroid 2000] • Approximate version of Verification Problem linear in formula/model [Bruns & Godefroid 1999] • If approximate version verifies abstraction, system also verified (soundness) • If approximate version doesn’t verify abstraction, system may still satisfy considered formula: under-approximation (incompleteness) 5 © Imperial College London

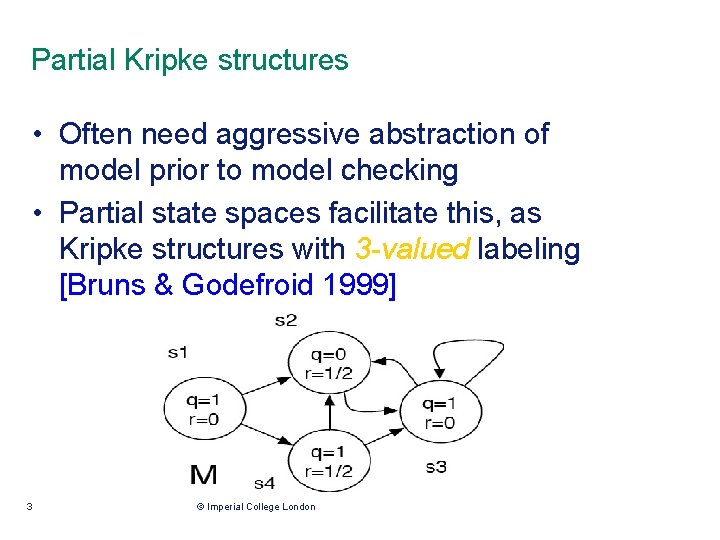
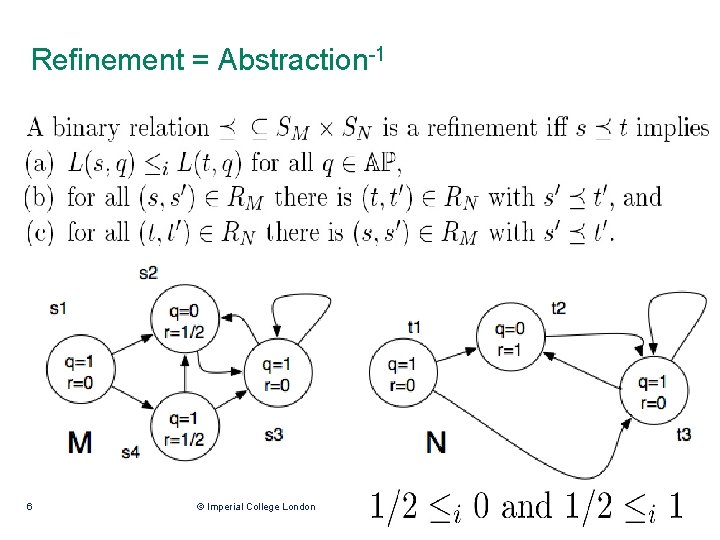
Refinement = Abstraction-1 6 © Imperial College London

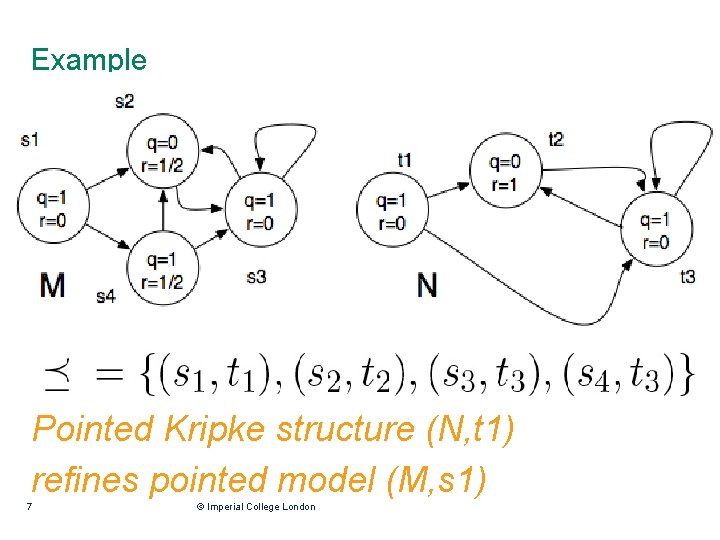
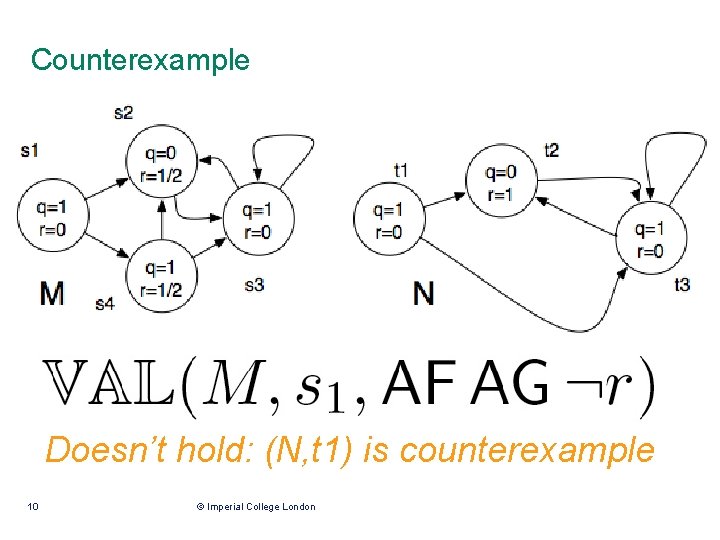
Example Pointed Kripke structure (N, t 1) refines pointed model (M, s 1) 7 © Imperial College London

Formal Verification Problem (M, s) pointed model: M with initial state s holds iff all pointed Kripke structures that refine (M, s) satisfy holds iff some pointed Kripke structure refines (M, s) and satisfies 8 © Imperial College London

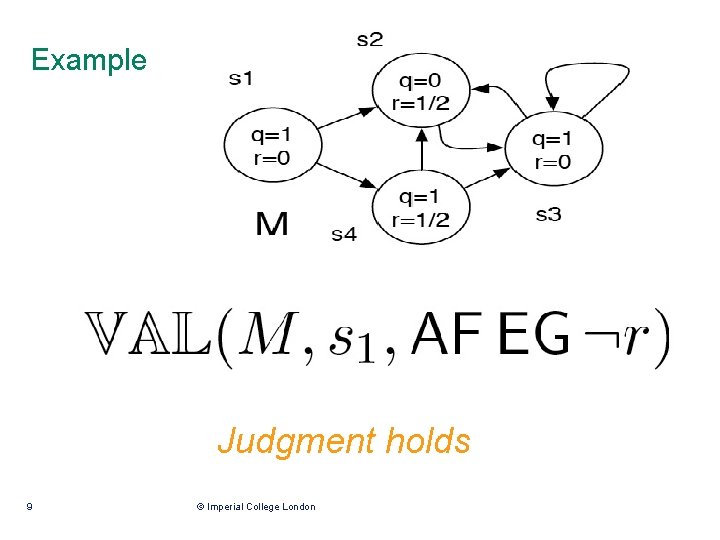
Example Judgment holds 9 © Imperial College London

Counterexample Doesn’t hold: (N, t 1) is counterexample 10 © Imperial College London

Approximate versions of judgments • Use semantics similar to labeling algorithm • Compositionally evaluate sub-formulas • Do this in pessimistic and in optimistic mode for • Pessimistic mode: under-approximates • Optimistic mode: over-approximates 11 © Imperial College London

Optimistic (o) and pessimistic (p) approximative semantics for mu-calculus Partial Kripke structure M = (S, R, L) 12 © Imperial College London

Formal soundness of approximation For sentence and for Soudness as two, co-dependent, implications: 13 © Imperial College London set

Incompleteness of approximation • If L(s, q) = 1/2, then the tautology holds at state s, but the pessimistic semantics won’t verify this. • But pessimistic semantics is complete for many practically relevant property patterns [Antonik & Huth 2006], e. g. “precedence chain: 2 stimuli, 1 response; globally, q and s precede r” patterns. project. cis. ksu. edu � 14 © Imperial College London

Making imprecise patterns precise All patterns at patterns. project. cis. ksu. edu are • either complete (already saw an example) • or become complete after trivial adjustments: is incomplete for verification, but its semantically equivalent version is complete for verification 15 © Imperial College London

Semantic self-minimization • Sentence pessimistically self-minimizing: Iff for all pointed models (M, s) • Sentence optimistically self-minimizing: Iff for all pointed models (M, s) 16 © Imperial College London

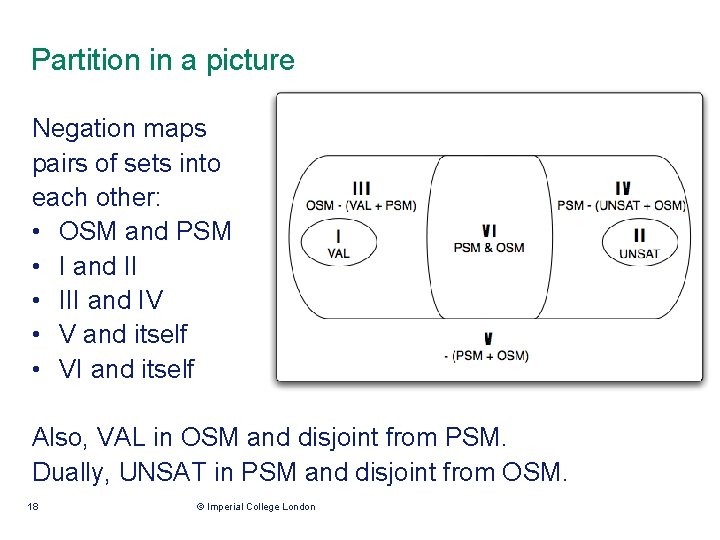
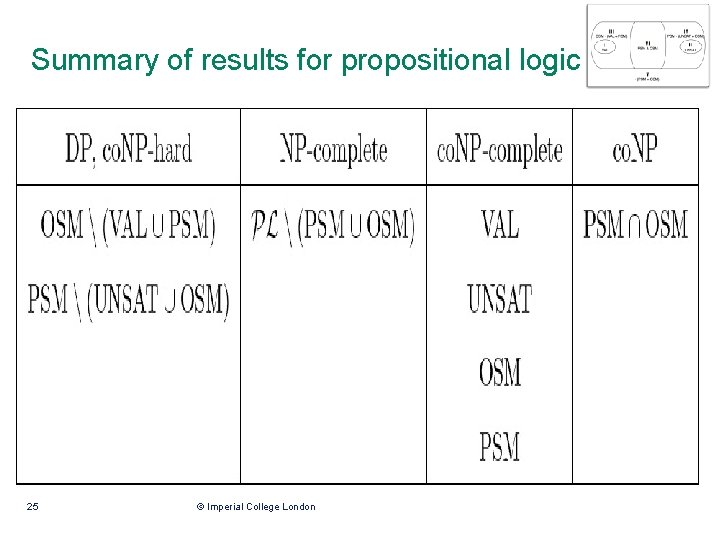
Decision Problems • OSM = set of optimistically self-minimizing sentences • PSM = set of pessimistically self-minimizing sentences • VAL = set of valid sentences • UNSAT = set of unsatisfiable sentences Study this for mu-calculus, modal logic, and propositional logic. 17 © Imperial College London

Partition in a picture Negation maps pairs of sets into each other: • OSM and PSM • I and II • III and IV • V and itself • VI and itself Also, VAL in OSM and disjoint from PSM. Dually, UNSAT in PSM and disjoint from OSM. 18 © Imperial College London

Set OSM, hardness result • Sentence in OSM iff its negation is in PSM • So OSM and PSM have same complexity • Deciding OSM at least as hard as deciding validity of logic: where x atomic proposition not occuring in • This is desired reduction to VAL: 19 © Imperial College London

Set OSM, upper bound for mu-calculus • For mu-calculus, OSM in 2 EXPTIME • From construct two alternating tree automata exponential blowup in worst case - and then do language inclusion check for these automata exponential in size of these automata [Godefroid & Huth 2005]: • This language inclusion checks “completeness half” of for all pointed models (M, s) 20 © Imperial College London

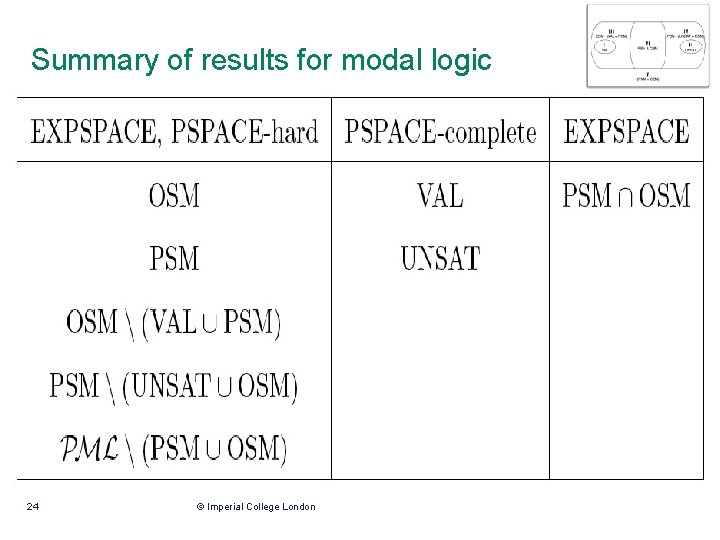
Set OSM, upper bound for modal logic • For modal logic, OSM in EXPSPACE • From construct two alternating tree automata as before, and again check • Both automata cannot distinguish trees at depths greater than size of (so called “shallow model property” of modal logic) • So the above check is in PSPACE in the size of the automata 21 © Imperial College London

Set OSM, exact bound for propositional logic • Already showed OSM is co. NP-hard • Show PL - OSM in NP: 22 © Imperial College London

Summary of results for mu-calculus 23 © Imperial College London

Summary of results for modal logic 24 © Imperial College London

Summary of results for propositional logic 25 © Imperial College London

PART 2 REPORT ON WORK ON REFINEMENT CHECKING OF MODAL TRANSITION SYSTEMS 26 © Imperial College London

Common implementations • For k > 1 pointed modal transition systems (Mi, si) there is least-fixed point algorithm on their product state space for deciding whether these k models have a common refinement • This algorithm is polynomial for fixed k • This problem becomes NP-hard for k=2 already if we can name states uniquely with propositions (i. e. “nominals” in “hybrid logic”) • This seems to be EXPTIME-complete in k [UNPUBLISHED] • There does not exist a unique “most abstract” common refinement in general. 27 © Imperial College London

Proof sketch for EXPTIME-hardness [unpublished] • Relies on EXPTIME = APSPACE • Takes alternating-time Turing machine A that computes some EXPTIME-complete problem • There is a polynomial P such that each input s of A has circular tape of length P(|s|) • For each input s of A, construct k > 1 modal transition systems where k and size of models are polynomial in |s| • Show: these k models have common refinement iff A has an accepting run for input s 28 © Imperial College London

Extensional refinement checking Let (M 1, s 1) and (M 2, s 2) be pointed modal transition systems. We write I(Mi, si) for the class of pointed labeled transition systems that refine (Mi, si). • Deciding whether I(M 1, s 1) is contained in I(M 2, s 2) appears to be PSPACE-hard in the sum of the sizes of M 1 and M 2. [UNPUBLISHED] 29 © Imperial College London

Proof sketch for PSPACE-hardness [unpublished] • QCNF, closed quantified Boolean formulas whose propositional bodies are in conjunctive normal form, e. g. x y z[ (x&!y) || !z || (!x&z)] • Computing truth values of QCNF is PSPACEcomplete problem • Given in QCNF, construct two modal transition systems N[ ] and M[ ] such that is false iff I(N[ ], t ) I(M[ ], s ) • This reduction works also for strict inclusion I(M 1, s 1) I(M 2, s 2), seems to work for disjunctive modal transition systems, but may not work for I(M 1, s 1) = I(M 2, s 2) 30 © Imperial College London

Thank you. 31 © Imperial College London

32 © Imperial College London

“Experimental” data • Used Perl script to randomly generate “all” formulas of propositional logic for sizes 1 to 5 • Size = number of occurrences of logical connectives in formula • Brute-force decision of membership: in OSM (~75%), in set VI (~50%), and in NP-complete set V (~2. 45%) • Less formulas seem to be in set VI as number of logical operators in formula increases 33 © Imperial College London