Model Based Control Strategies Model Based Control 1

Model Based Control Strategies

Model Based Control • 1 - Inverse Model as a Forward Controller (Inverse Dynamics) • 2 - Forward Model in Feedback • 3 - Combination of above

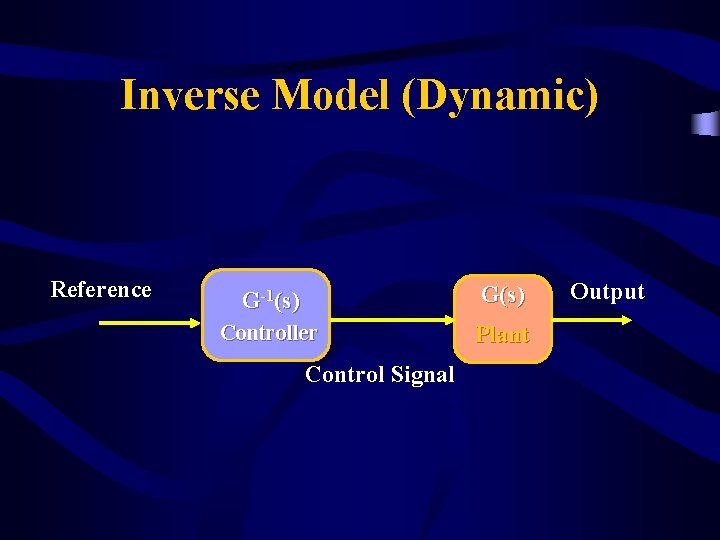
Inverse Model (Dynamic) Reference G-1(s) G(s) Controller Plant Control Signal Output

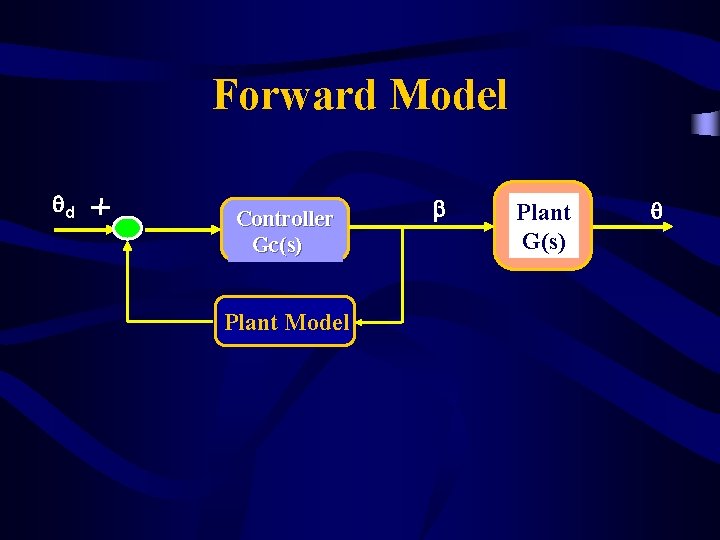
Forward Model qd Controller Gc(s) Plant Model b Plant G(s) q

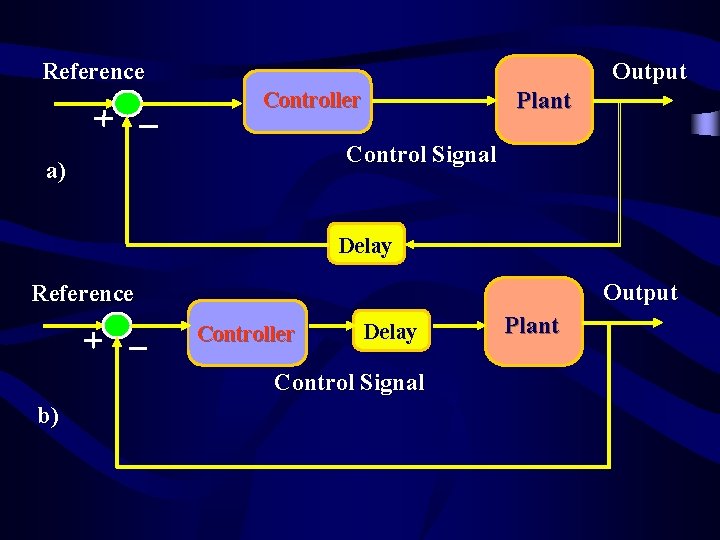
Reference Output Plant Controller Control Signal a) Delay Output Reference Controller Delay Control Signal b) Plant

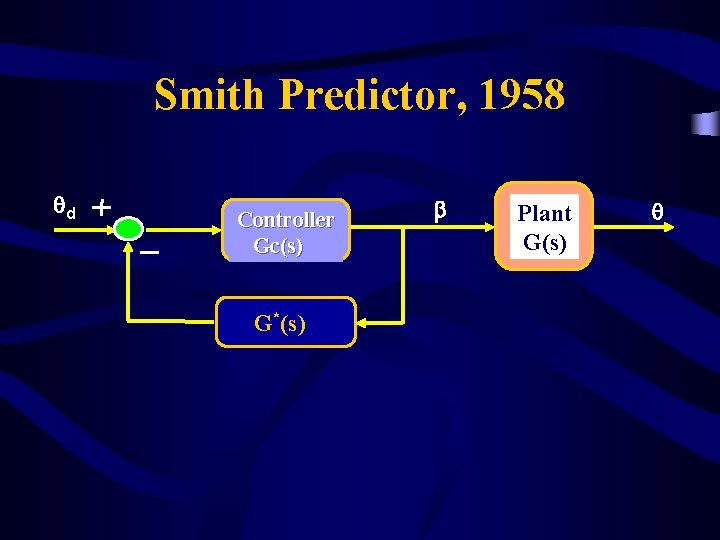
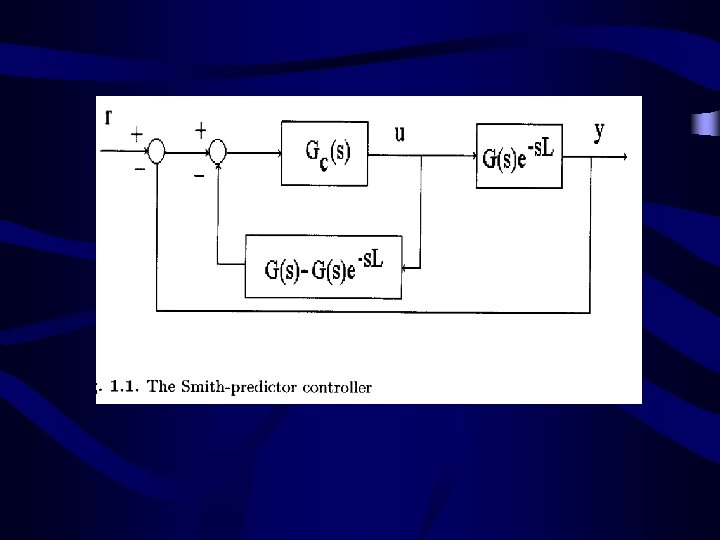
Smith Predictor, 1958 qd Controller Gc(s) G*(s) b Plant G(s) q

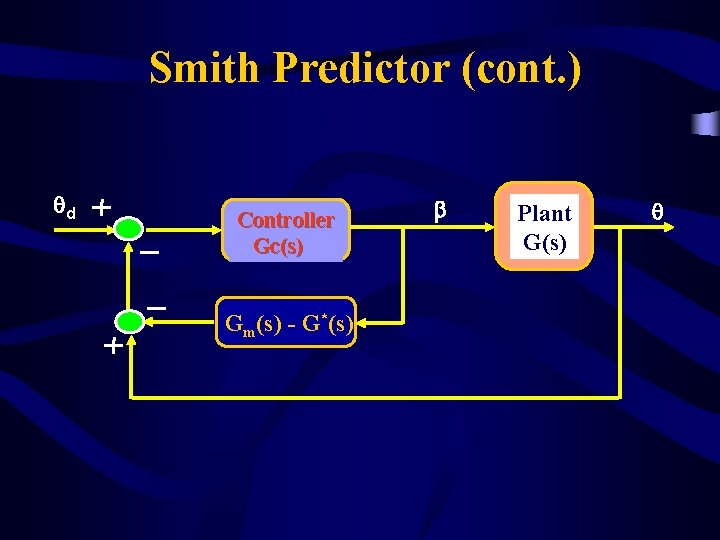
Smith Predictor (cont. ) qd Controller Gc(s) Gm(s) - G*(s) b Plant G(s) q

Miall, R. C. , Weir, D. J. , Wolpert, D. M. , and Stein, J. F. , (1993), "Is the Cerebellum a Smith Predictor ? ", Journal of Motor Behavior, 25, 203 -216.

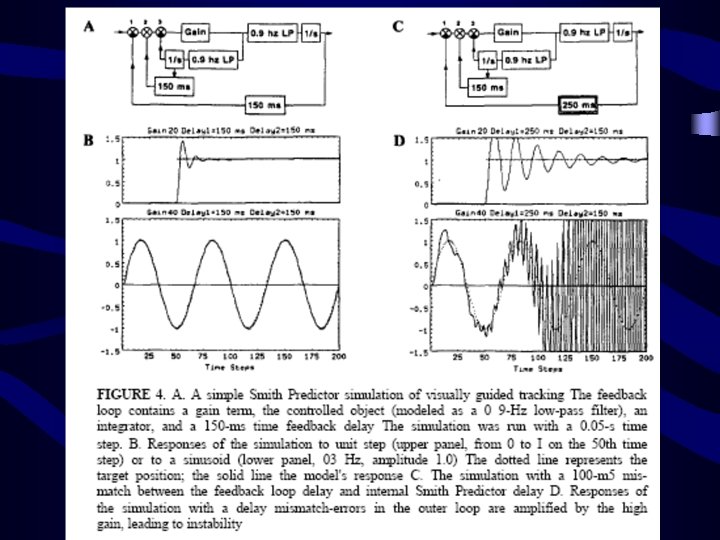
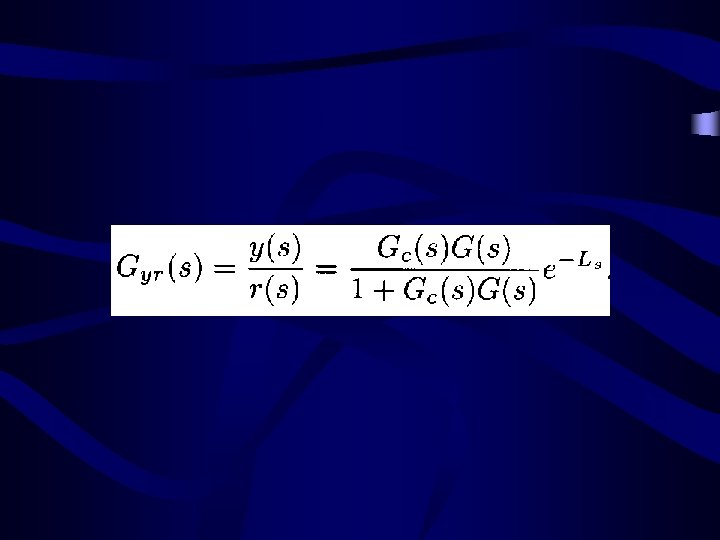
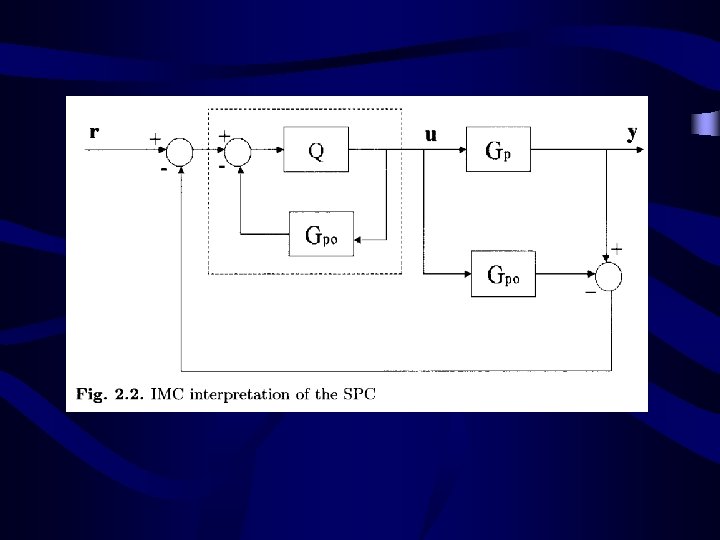
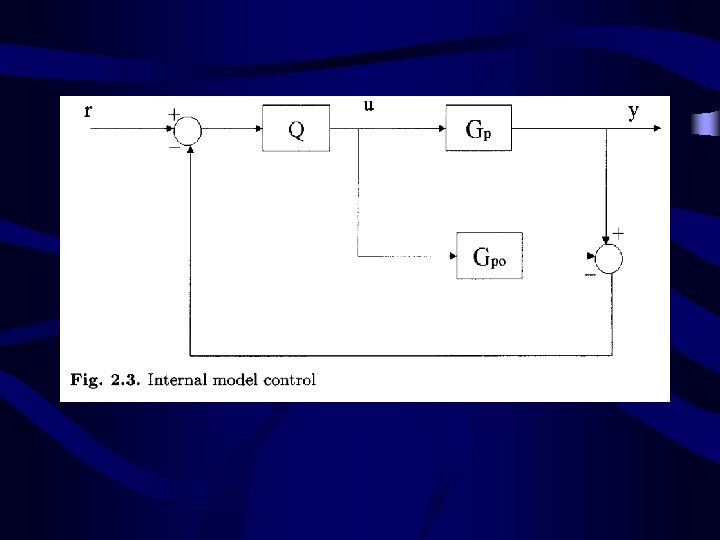
Model Predictive Control (MPC) 1. Receding (Finite) Horizon Control 2. Using Time (Impulse/Step) Response 3. Based on Optimal Control with Constraints

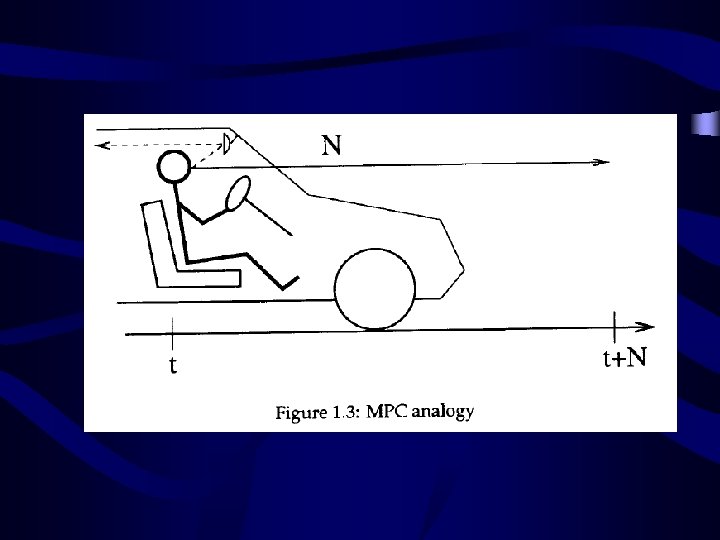
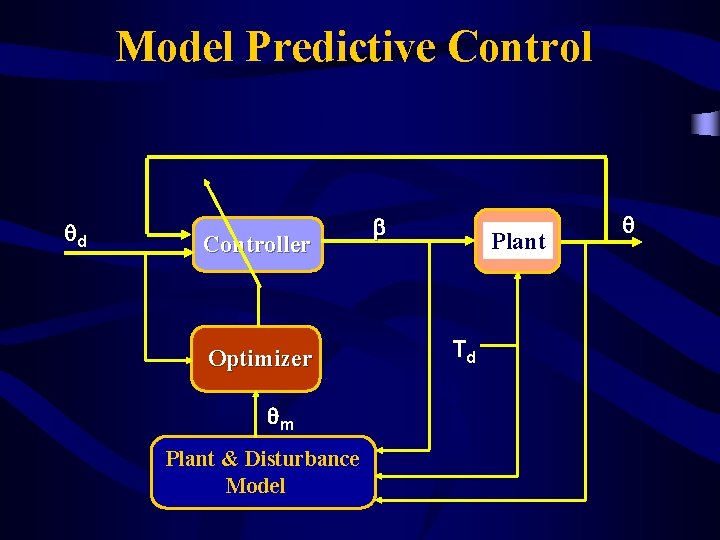
Model Predictive Control qd Controller Optimizer qm Plant & Disturbance Model b Plant Td q

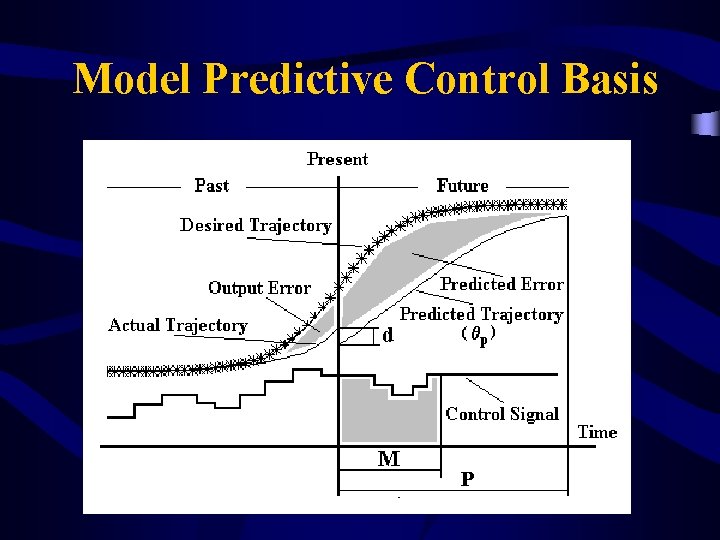
Model Predictive Control Basis

Smith Predictor & MPC Comparison

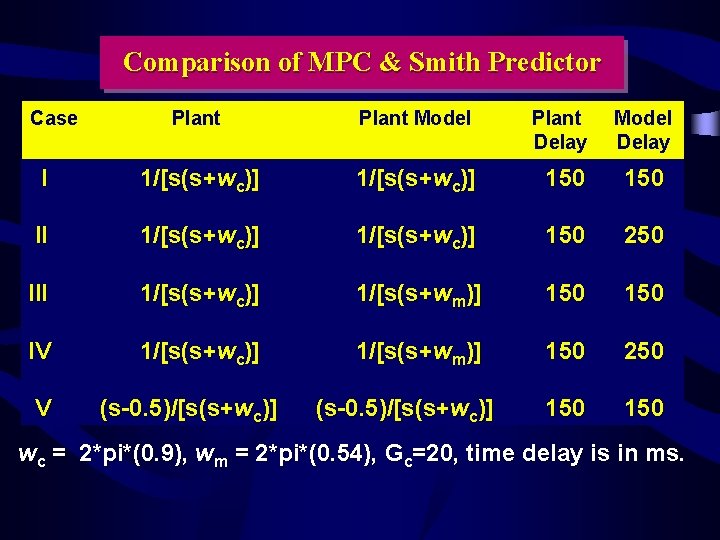
Comparison of MPC & Smith Predictor Case Plant Model Plant Delay Model Delay I 1/[s(s+wc)] 150 II 1/[s(s+wc)] 150 250 III 1/[s(s+wc)] 1/[s(s+wm)] 150 IV 1/[s(s+wc)] 1/[s(s+wm)] 150 250 150 V (s-0. 5)/[s(s+wc)] wc = 2*pi*(0. 9), wm = 2*pi*(0. 54), Gc=20, time delay is in ms.

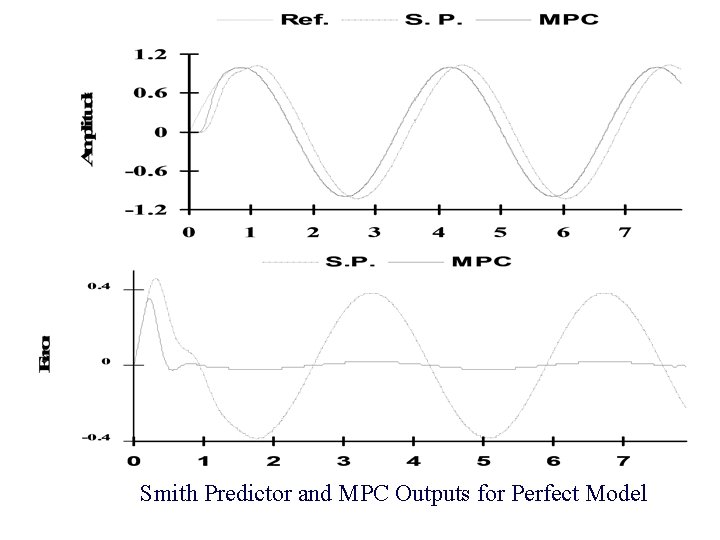
Smith Predictor and MPC Outputs for Perfect Model Time (s)

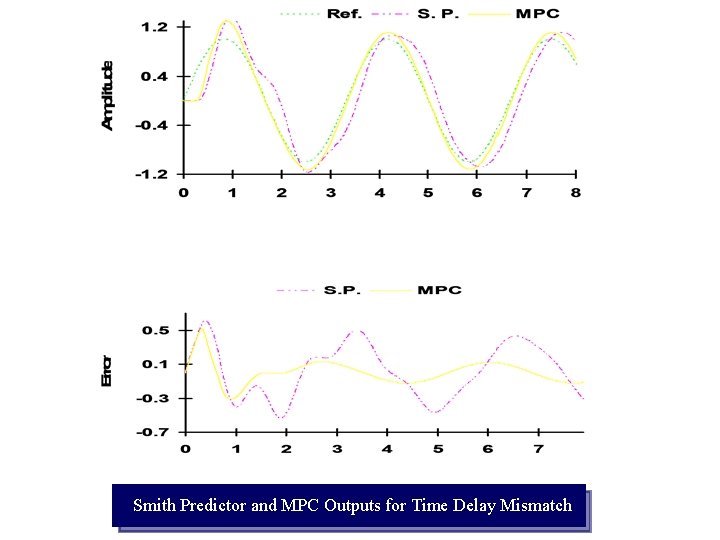
Time (s) Smith Predictor and MPC Outputs for Time Delay Mismatch

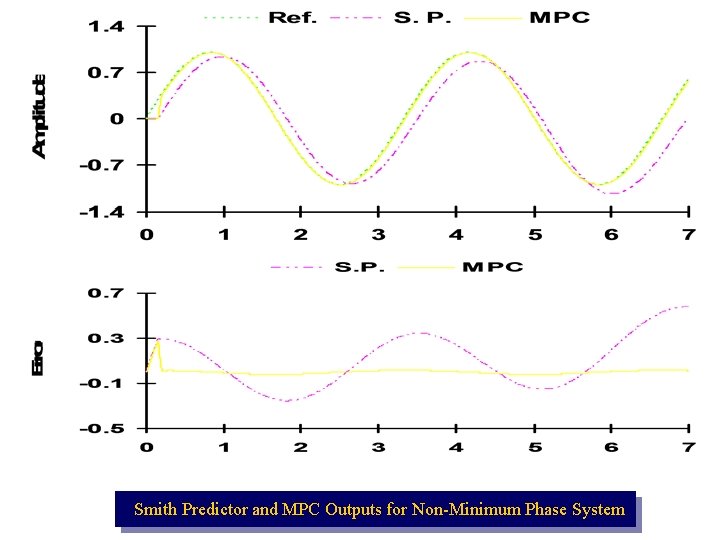
Time (s) Smith Predictor and MPC Outputs for Non-Minimum Phase System

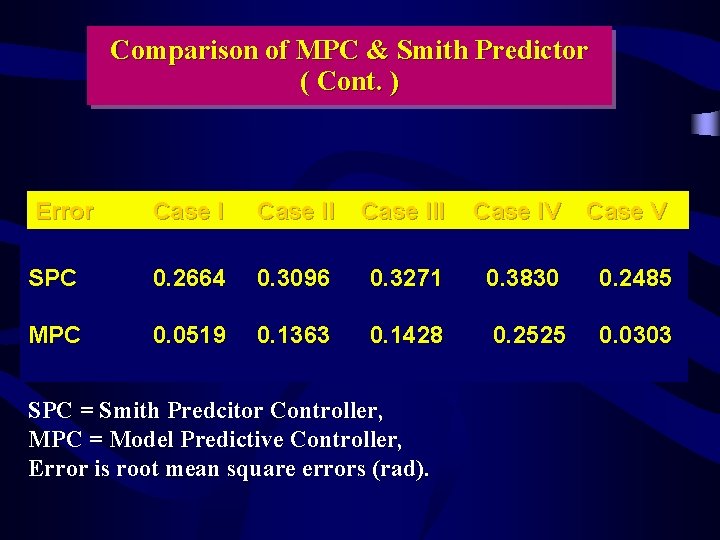
Comparison of MPC & Smith Predictor ( Cont. ) Error Case III Case IV Case V SPC 0. 2664 0. 3096 0. 3271 0. 3830 0. 2485 MPC 0. 0519 0. 1363 0. 1428 0. 2525 0. 0303 SPC = Smith Predcitor Controller, MPC = Model Predictive Controller, Error is root mean square errors (rad).