Mobile Robot Kinematics 3 Amirkabir University of Technology

Mobile Robot Kinematics ﺳیﻨﻤﺎﺗیک ﺩکﺘﺮ ﺳﻌیﺪ ﺷیﺮی ﻗیﺪﺍﺭی کﺘﺎﺏ 3 & ﻓﺼﻞ Amirkabir University of Technology Computer Engineering & Information Technology Department

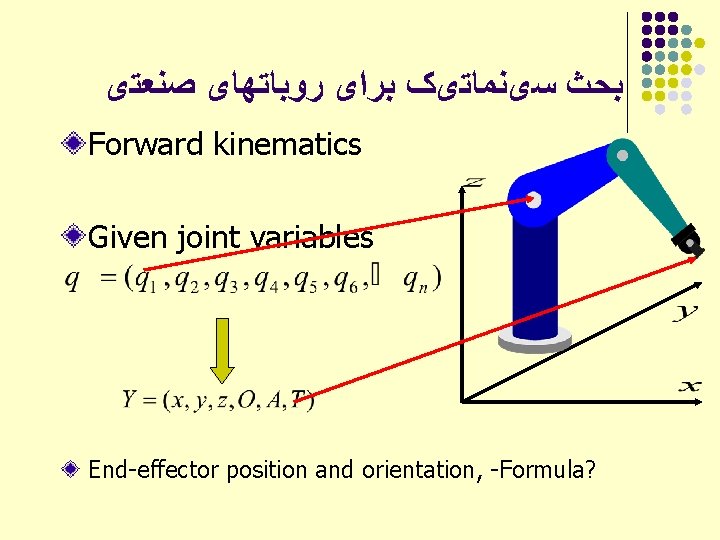
ﺑﺤﺚ ﺳیﻨﻤﺎﺗیک ﺑﺮﺍی ﺭﻭﺑﺎﺗﻬﺎی ﺻﻨﻌﺘی Forward kinematics Given joint variables End-effector position and orientation, -Formula?
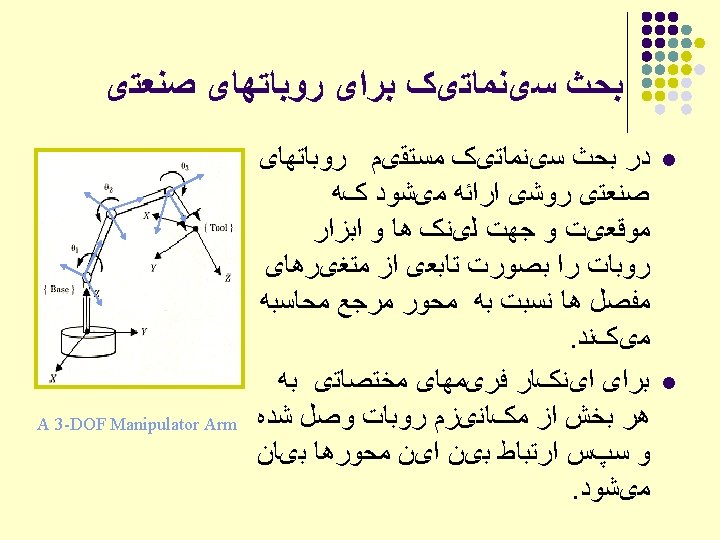
ﺑﺤﺚ ﺳیﻨﻤﺎﺗیک ﻣﻌکﻮﺱ ﺑﺮﺍی ﺭﻭﺑﺎﺗﻬﺎی ﺻﻨﻌﺘی Given a desired position (P) & orientation (R) of the endeffector Find the joint variables which can bring the robot the desired configuration

Inverse Kinematics K-1 (q 1 … q n) (x, y, z, qx, qy, qz)

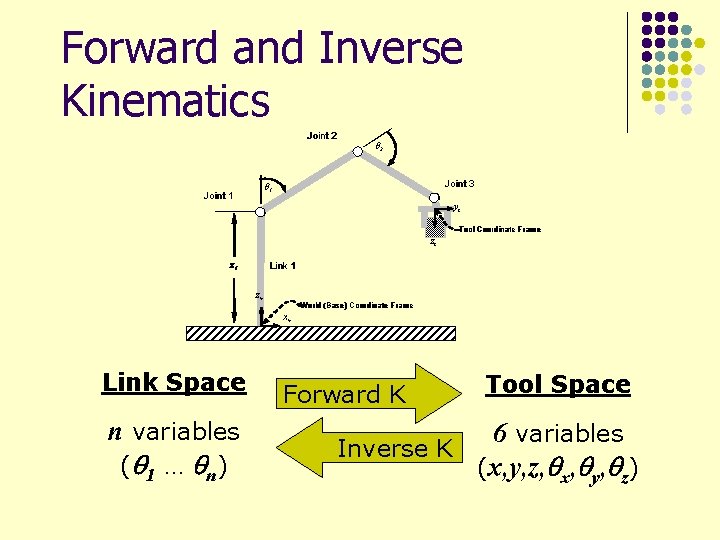
Forward and Inverse Kinematics Joint 2 q 2 Joint 3 q 1 Joint 1 yt Tool Coordinate Frame zt z 11 Link 1 zw World (Base) Coordinate Frame xw Link Space n variables (q 1 … q n) Forward K Tool Space 6 variables Inverse K (x, y, z, qx, qy, qz)




ﺿﺮﺏ ﺩﺍﺧﻠی Let and be arbitrary vectors in the angle from to , then and be Where q is the angle between the vectors and is the norm. X. Y=0 if X is perpendicular to Y.
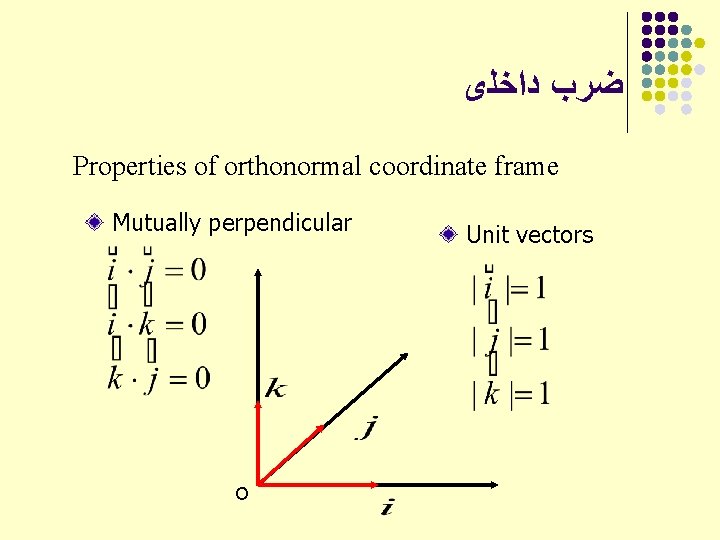
ﺿﺮﺏ ﺩﺍﺧﻠی Properties of orthonormal coordinate frame Mutually perpendicular O Unit vectors

ﻧﻤﺎیﺶ ﻧﻘﻄﻪ ﻭ ﺑﺮﺩﺍﺭ Point represented in OXYZ: Vector represented in OXYZ: O, O’
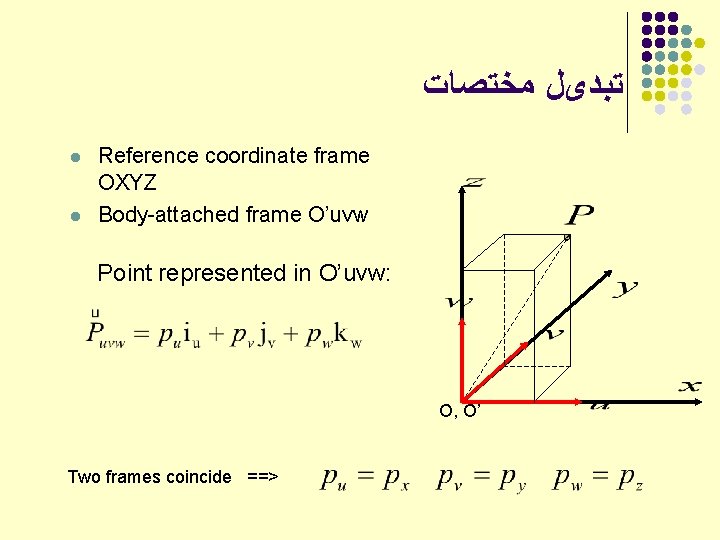
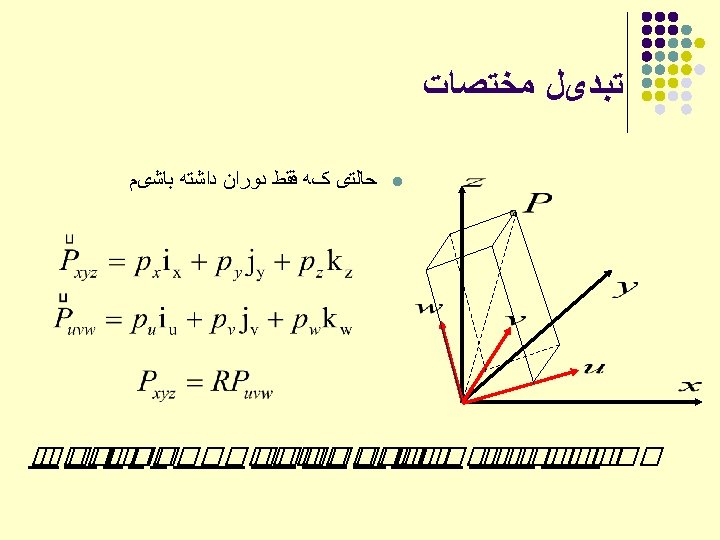
ﺗﺒﺪیﻞ ﻣﺨﺘﺼﺎﺕ l l Reference coordinate frame OXYZ Body-attached frame O’uvw Point represented in O’uvw: O, O’ Two frames coincide ==>

ﺣﺎﻟﺖ ﺩﻭﺭﺍﻥ ﺳﺎﺩﻩ Px , Py , and Pz represent the projections of P onto OX, OY, OZ axes, respectively Since
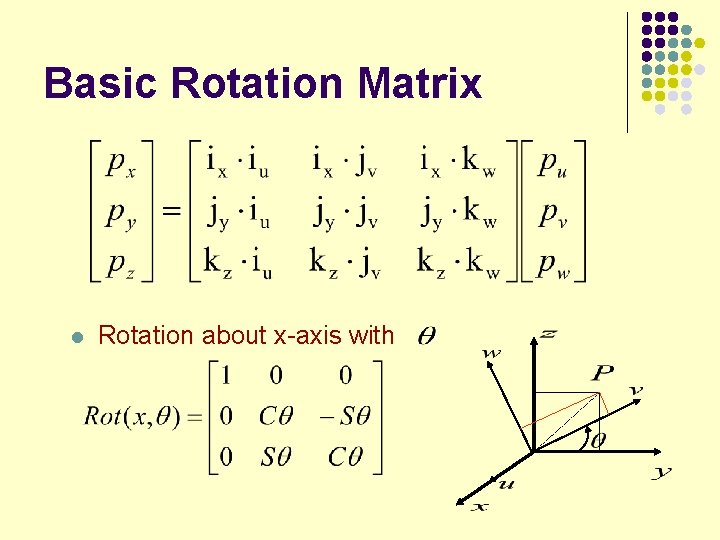
Basic Rotation Matrix l Rotation about x-axis with

Basic Rotation Matrix Rotation about x axis with

Basic Rotation Matrices Rotation about x-axis with q Rotation about y-axis with q Rotation about z-axis with q

Basic Rotation Matrix Obtain the coordinate of from the coordinate of Dot products are commutative! <== 3 X 3 identity matrix

Example A point is attached to a rotating frame, the frame rotates 60 degree about the OZ axis of the reference frame. Find the coordinates of the point relative to the reference frame after the rotation.

Composite Rotation Matrix A sequence of finite rotations Matrix multiplications do not commute Rules: If rotating coordinate O-U-V-W is rotating about principal axis of OXYZ frame, then pre-multiply the previous (resultant) rotation matrix with an appropriate basic rotation matrix If rotating coordinate OUVW is rotating about its own principal axes, then post-multiply the previous (resultant) rotation matrix with an appropriate basic rotation matrix

Example Find the rotation matrix for the following operations: Pre-multiply if rotate about the OXYZ axes Post-multiply if rotate about the OUVW axes

Coordinate Transformations • position vector of P in {B} is transformed to position vector of P in {A} • description of {B} as seen from an observer in {A} Rotation of {B} with respect to {A} Translation of the origin of {B} with respect to origin of {A}
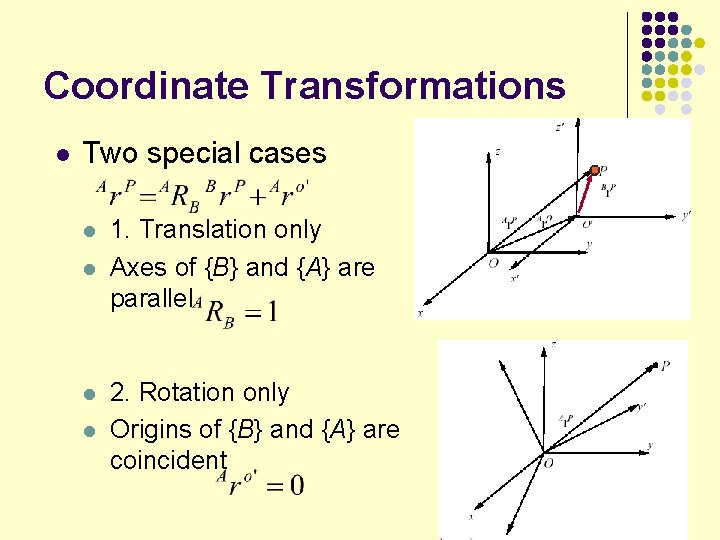
Coordinate Transformations l Two special cases l l 1. Translation only Axes of {B} and {A} are parallel 2. Rotation only Origins of {B} and {A} are coincident
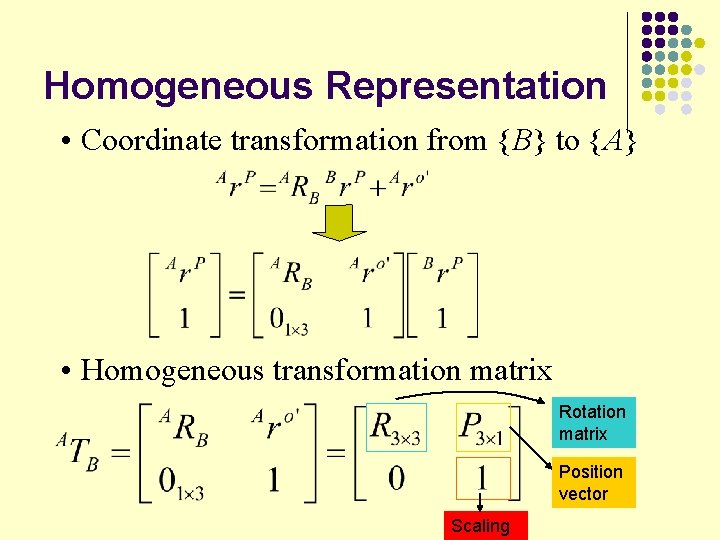
Homogeneous Representation • Coordinate transformation from {B} to {A} • Homogeneous transformation matrix Rotation matrix Position vector Scaling

Homogeneous Transformation Special cases 1. Translation 2. Rotation l
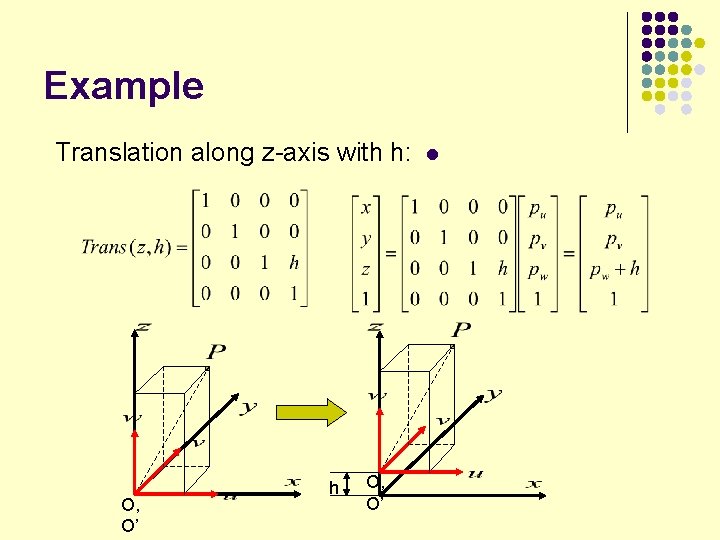
Example Translation along z-axis with h: O, O’ h O, O’ l
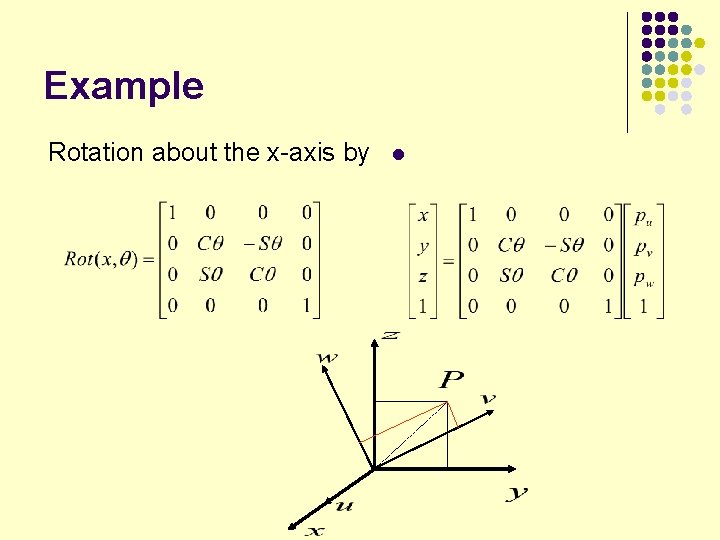
Example Rotation about the x-axis by l

Example Find the homogeneous transformation matrix (T) for the following operation: l

Homogeneous Representation A frame in space (geometric interpretation) l Principal axis n w. r. t. the reference coordinate system
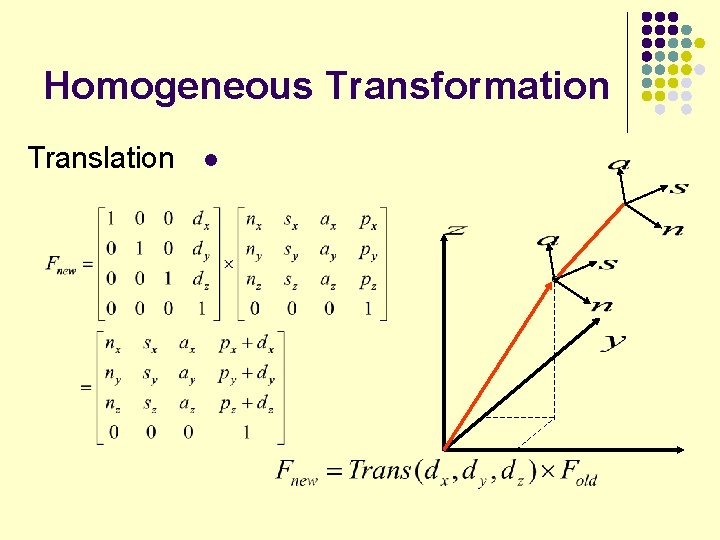
Homogeneous Transformation Translation l
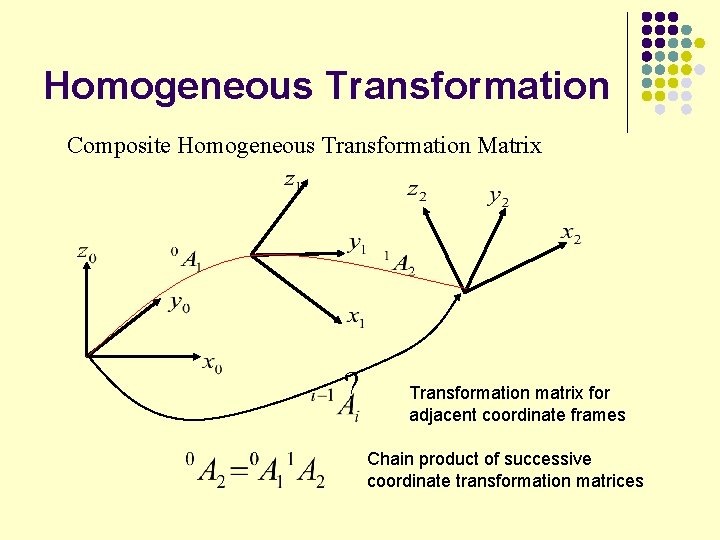
Homogeneous Transformation Composite Homogeneous Transformation Matrix ? Transformation matrix for adjacent coordinate frames Chain product of successive coordinate transformation matrices

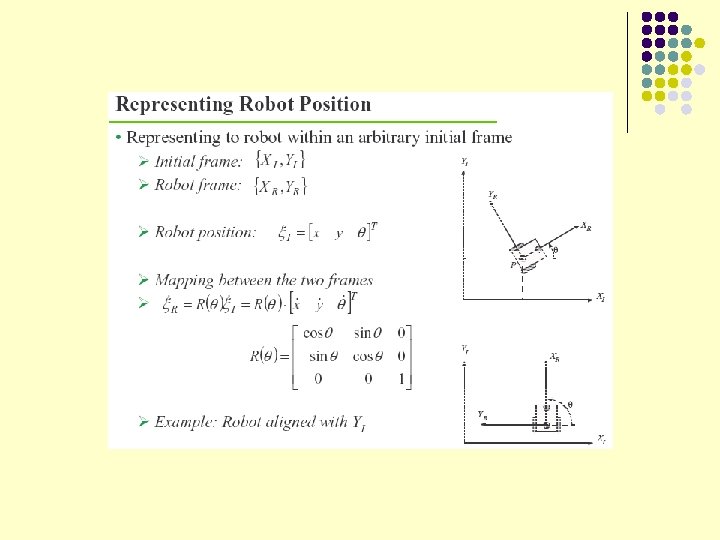
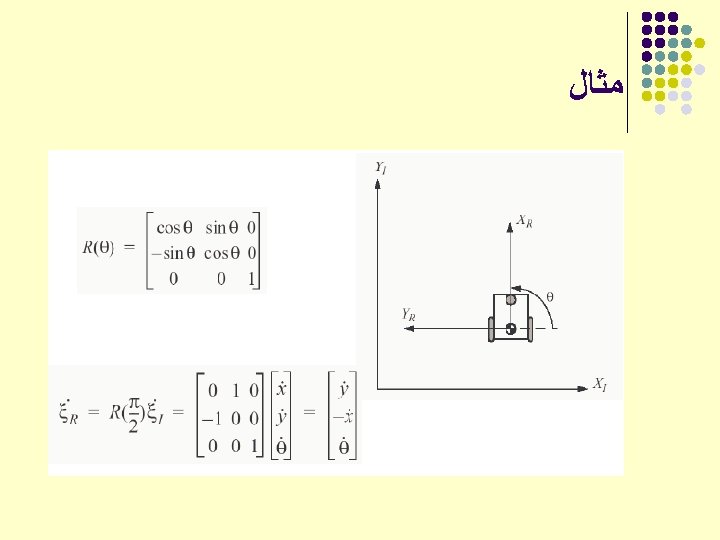
Homogeneous Transformations With respect to the universal frame , the position of is:

Homogeneous Transformations This equation can be reduced in a very l handsome way by introducing homogenous coordinates and transformation.

Minimal Representation of Orientation










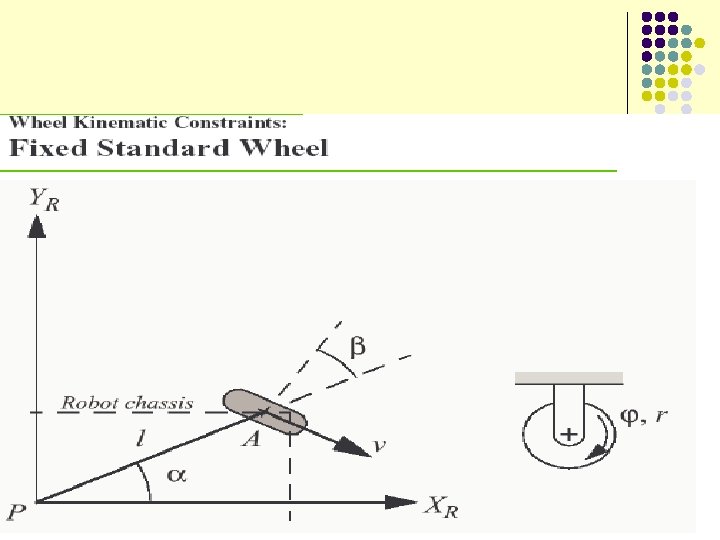

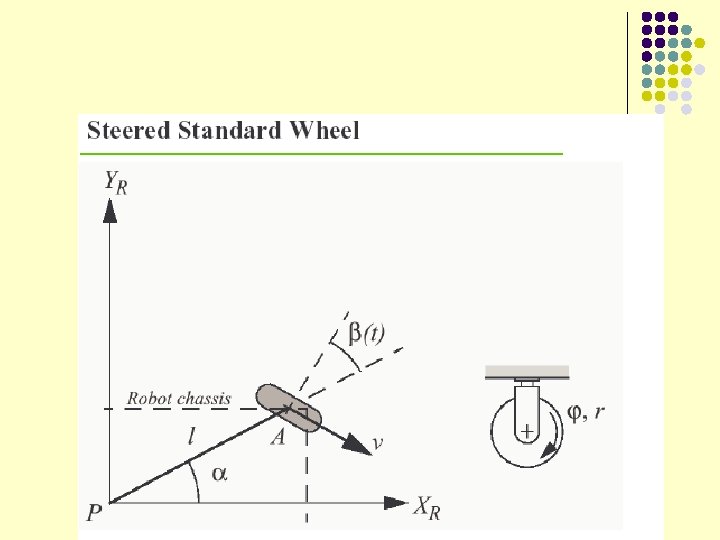
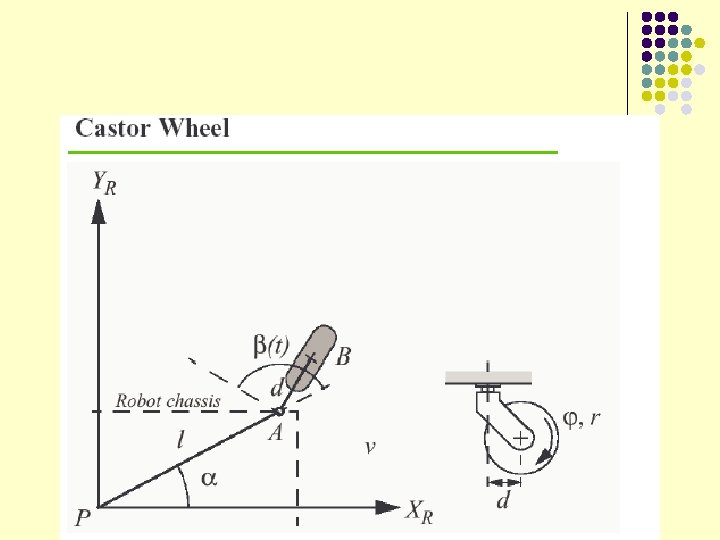
- Slides: 53