MO Diagrams for More Complex Molecules Chapter 5

MO Diagrams for More Complex Molecules Chapter 5 Friday, October 16, 2015

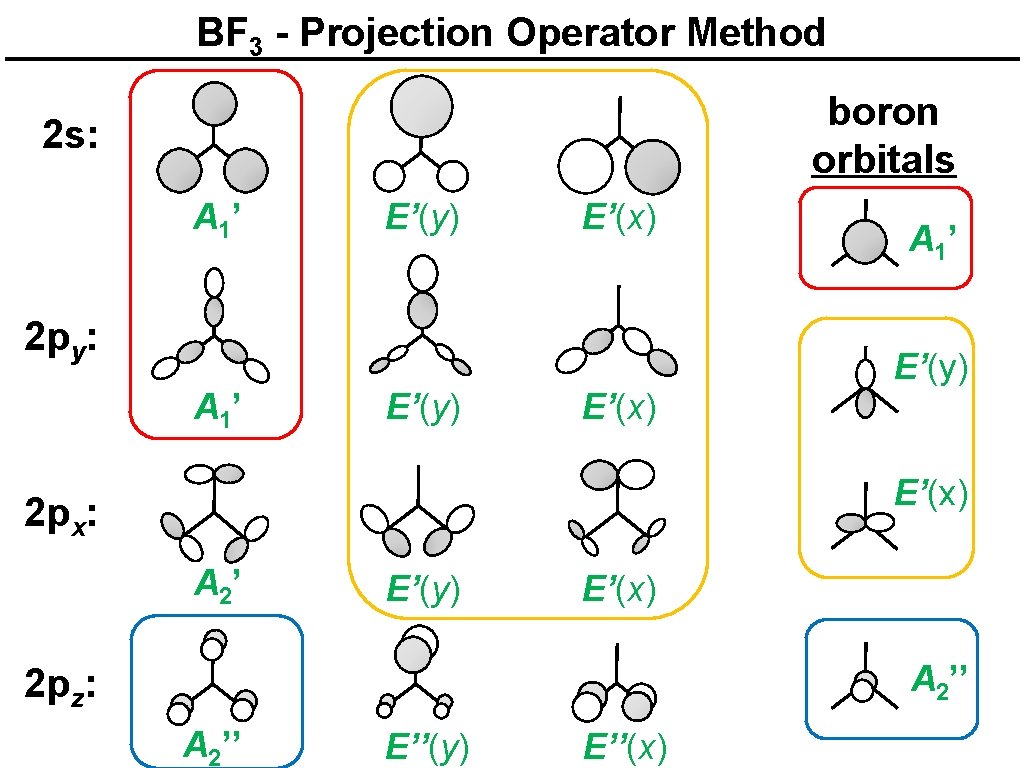
BF 3 - Projection Operator Method boron orbitals 2 s: A 1’ E’(y) E’(x) 2 py: A 1’ E’(y) E’(x) 2 px: A 2’ E’(y) E’(x) A 2’’ 2 pz: A 2’’ E’’(y) E’’(x)

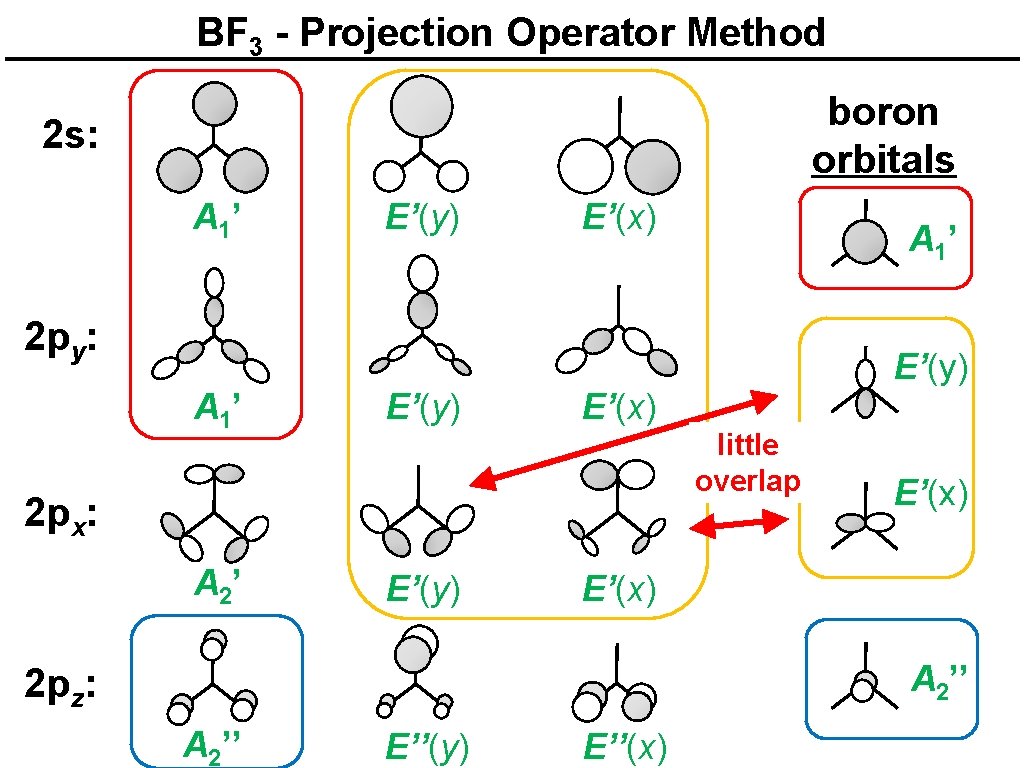
BF 3 - Projection Operator Method boron orbitals 2 s: A 1’ E’(y) E’(x) A 1’ 2 py: A 1’ E’(y) E’(x) little overlap 2 px: A 2’ E’(y) E’(x) A 2’’ 2 pz: A 2’’ E’’(y) E’’(x)

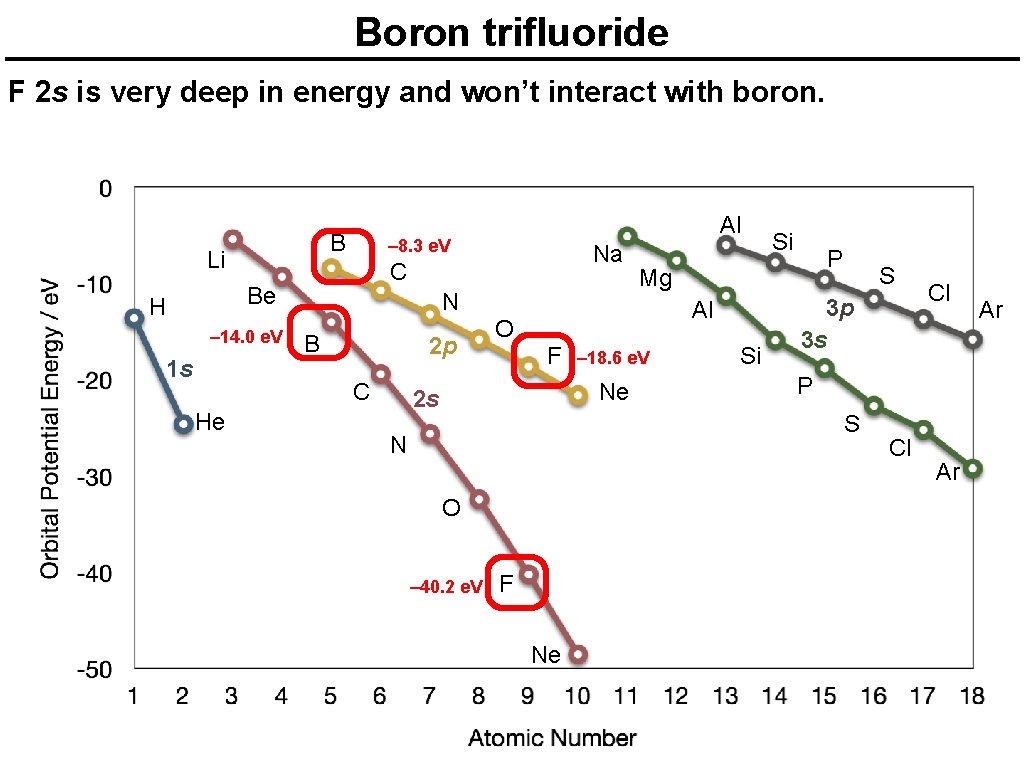
Boron trifluoride F 2 s is very deep in energy and won’t interact with boron. B Li – 8. 3 e. V – 14. 0 e. V 1 s N B 2 p C He Na C Be H Al O – 18. 6 e. V Ne 2 s P Mg Al F Si Si S 3 p 3 s P S N O – 40. 2 e. V F Ne Cl Cl Ar Ar

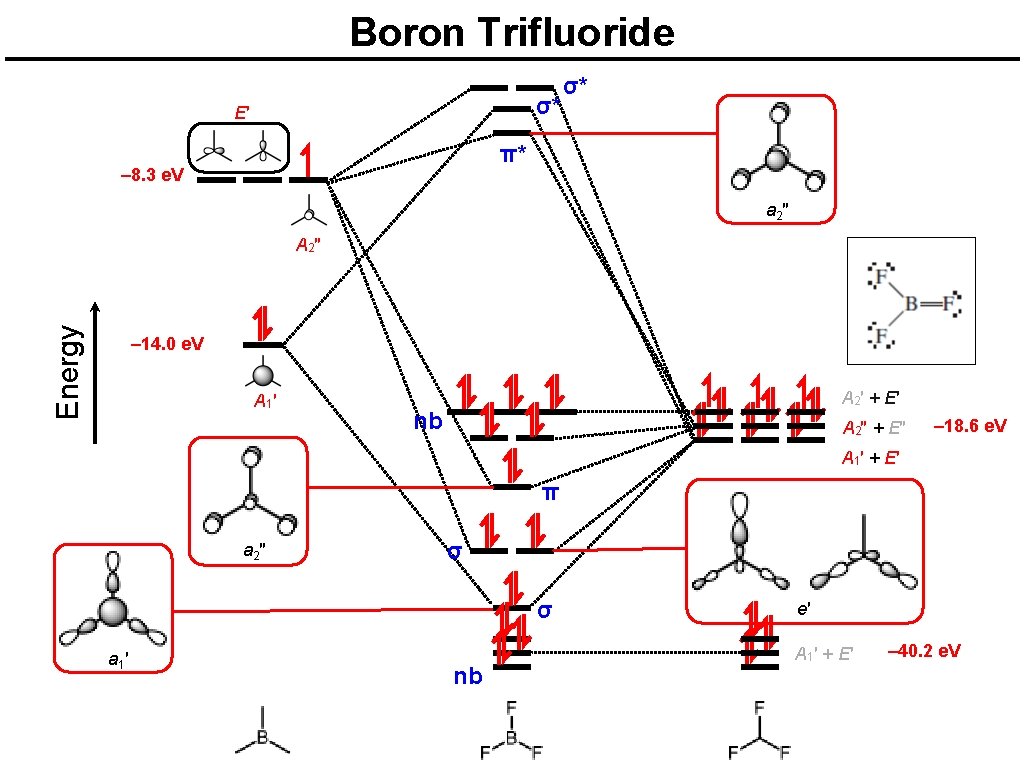
Boron Trifluoride σ* E′ σ* π* – 8. 3 e. V a 2 ″ Energy A 2″ – 14. 0 e. V A 1′ A 2′ + E′ nb A 2″ + E″ – 18. 6 e. V A 1′ + E′ π a 2 ″ σ σ a 1 ′ nb e′ A 1′ + E′ – 40. 2 e. V

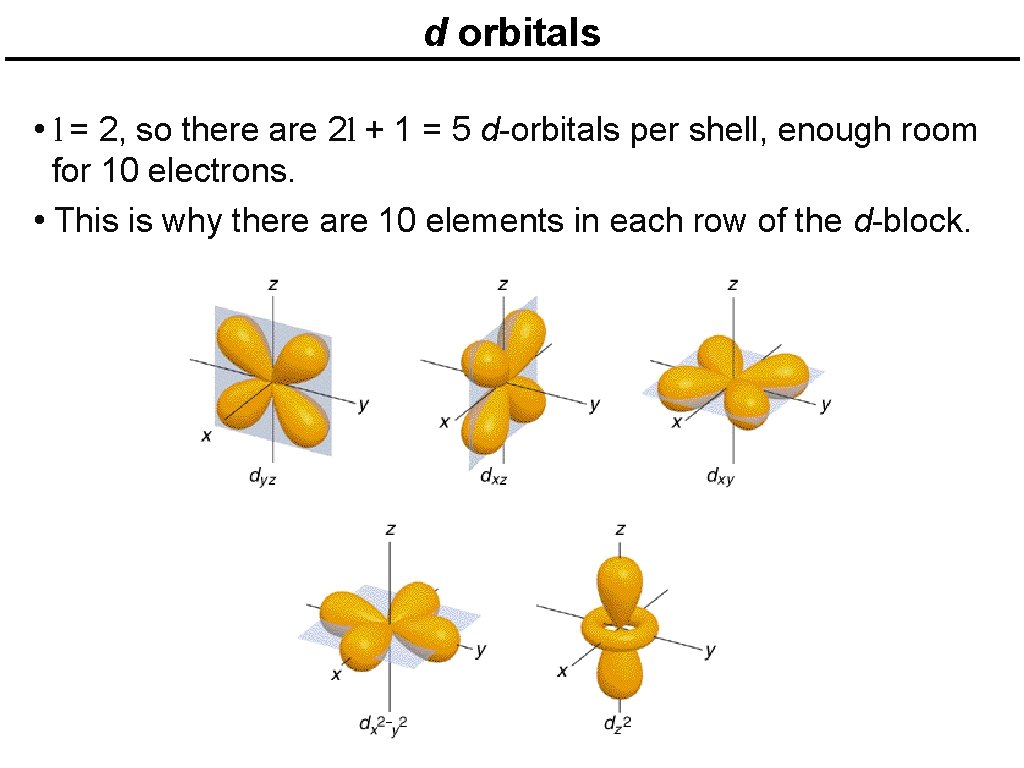
d orbitals • l = 2, so there are 2 l + 1 = 5 d-orbitals per shell, enough room for 10 electrons. • This is why there are 10 elements in each row of the d-block.

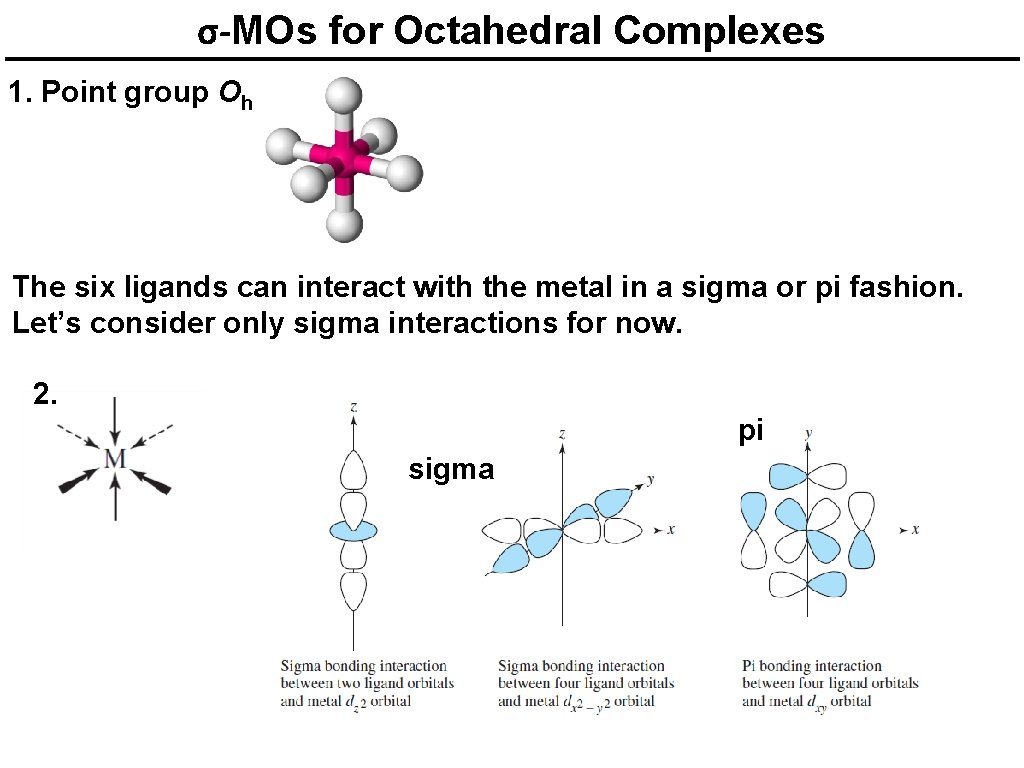
σ-MOs for Octahedral Complexes 1. Point group Oh The six ligands can interact with the metal in a sigma or pi fashion. Let’s consider only sigma interactions for now. 2. pi sigma

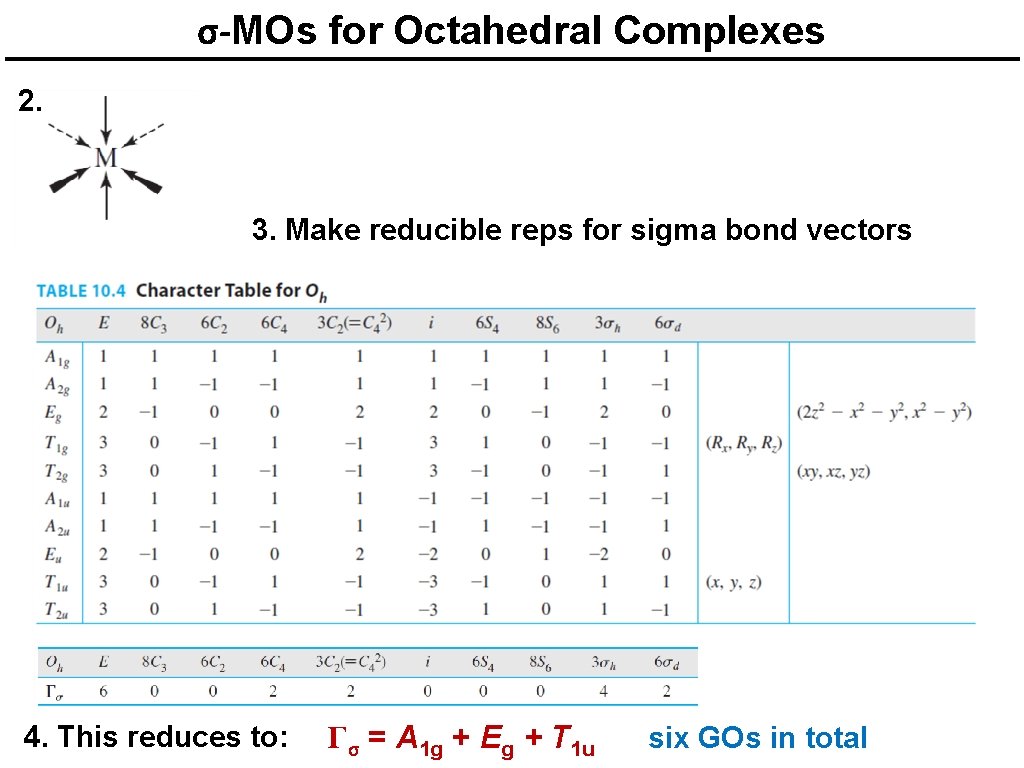
σ-MOs for Octahedral Complexes 2. 3. Make reducible reps for sigma bond vectors 4. This reduces to: Γσ = A 1 g + Eg + T 1 u six GOs in total

σ-MOs for Octahedral Complexes 5. Find symmetry matches with central atom. Γσ = A 1 g + Eg + T 1 u Reading off the character table, we see that the group orbitals match the metal s orbital (A 1 g), the metal p orbitals (T 1 u), and the dz 2 and dx 2 -y 2 metal d orbitals (Eg). We expect bonding/antibonding combinations. The remaining three metal d orbitals are T 2 g and σ-nonbonding.

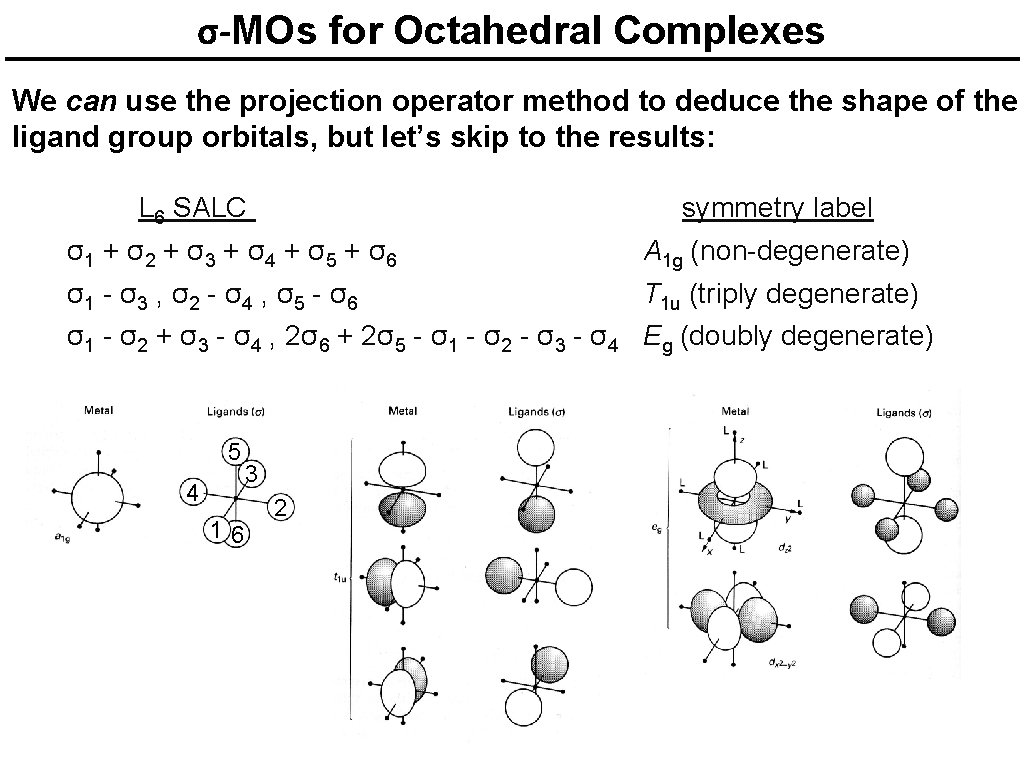
σ-MOs for Octahedral Complexes We can use the projection operator method to deduce the shape of the ligand group orbitals, but let’s skip to the results: L 6 SALC symmetry label σ1 + σ2 + σ3 + σ4 + σ5 + σ6 A 1 g (non-degenerate) σ1 - σ3 , σ2 - σ4 , σ5 - σ6 T 1 u (triply degenerate) σ1 - σ2 + σ3 - σ4 , 2σ6 + 2σ5 - σ1 - σ2 - σ3 - σ4 Eg (doubly degenerate) 5 4 16 3 2

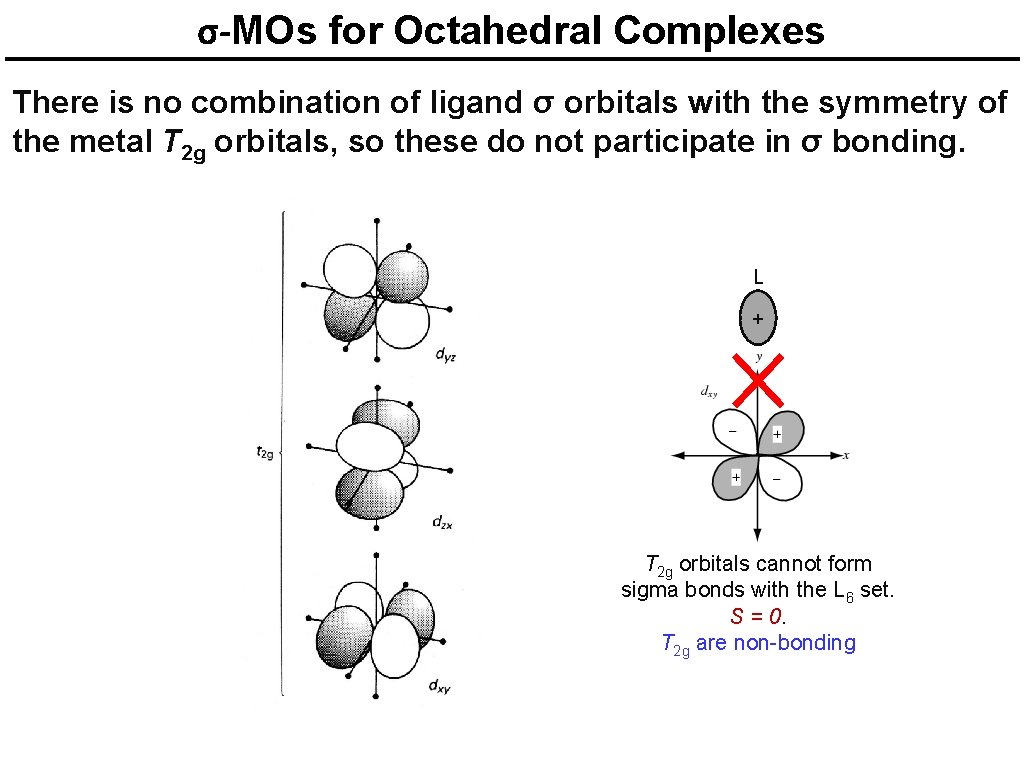
σ-MOs for Octahedral Complexes There is no combination of ligand σ orbitals with the symmetry of the metal T 2 g orbitals, so these do not participate in σ bonding. L + T 2 g orbitals cannot form sigma bonds with the L 6 set. S = 0. T 2 g are non-bonding

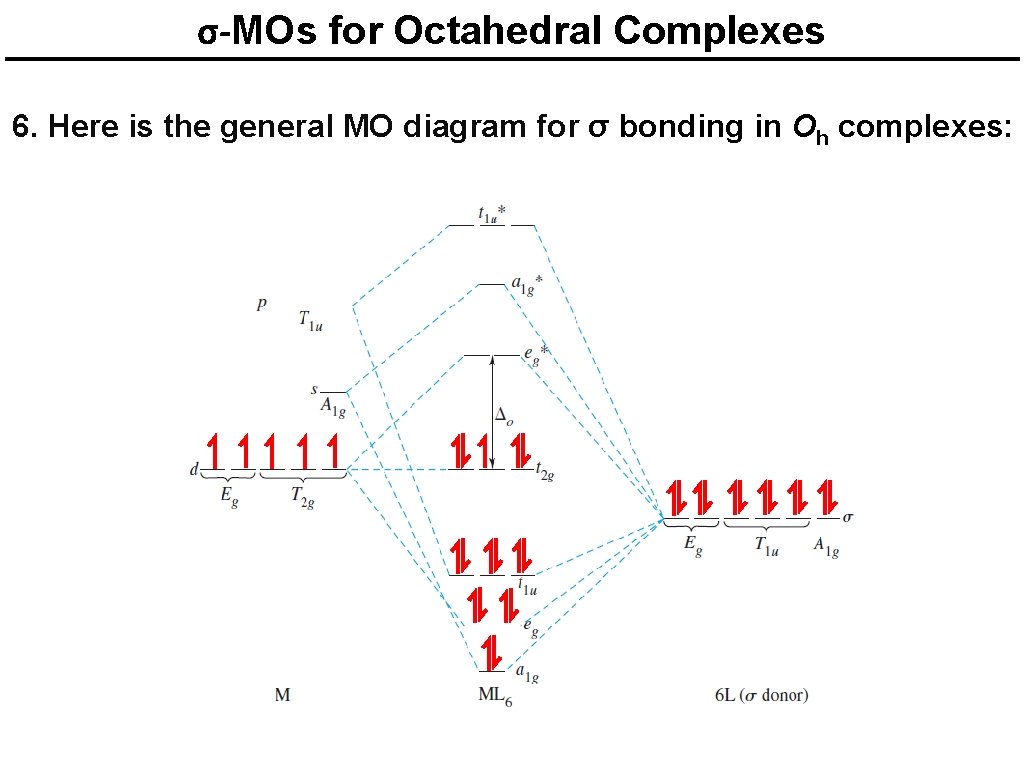
σ-MOs for Octahedral Complexes 6. Here is the general MO diagram for σ bonding in Oh complexes:

Summary MO Theory • MO diagrams can be built from group orbitals and central atom orbitals by considering orbital symmetries and energies. • The symmetry of group orbitals is determined by reducing a reducible representation of the orbitals in question. This approach is used only when the group orbitals are not obvious by inspection. • The wavefunctions of properly-formed group orbitals can be deduced using the projection operator method. • We showed the following examples: homonuclear diatomics, HF, CO, H 3+, FHF-, CO 2, H 2 O, BF 3, and σ-ML 6