Mlhavost Fuzzy logika fuzzy mnoiny fuzzy sla Mlhavost

Mlhavost Fuzzy logika, fuzzy množiny, fuzzy čísla

Mlhavost • Možné příčiny nejistoty: – Stochastický charakter jevu (zítra bude pršet). – Kvantová nejistota (teplota vody v umyvadle je 10 stupňů) – Mlhavost pojmů (jsem vysoký člověk)

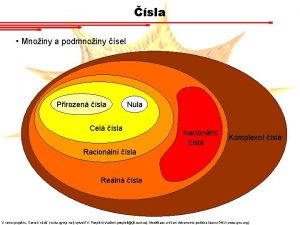
Fuzzy množiny • Klasická teorie množin : – prvek do množiny patří, nebo nepatří. • Existuje charakteristická funkce množiny A. – MA = 1, pokud x A, – MA = 0, pokud není x A. • Fuzzy množina je určena svou charakteristickou funkcí μA z univerza U na interval <0, 1> – μA (x)= 1, pokud x je určitě v A. – μA (x)= 0, pokud x určitě není v A. – μA je mezi 0 a 1, pokud nevíme jistě, zda x je v A, nebo není.

Fuzzy množiny • • • Nosič A: supp(A)={x U|μA (x) > 0}. Jádro A: core(A)={x U|μA (x) = 1}. Výška fuzzy množiny: sup(μA (x)). Normální fuzzy množina: Výška je rovna 1. α-hladina fuzzy množiny A {x U|μA (x) ≥ α}. α-řez fuzzy množiny A {x U|μA (x) = α}.

Operace s fuzzy množinami • A je podmnožina of B: μA (x) ≤ μB(x) • B je doplněk of A: μB(x) = 1 - μA(x) • C je (standardní) sjednocení A a B: μC(x)=max(μA(x), μB(x)) • C je (standardní) průnik A a B: μC(x)=min(μA(x), μB(x))

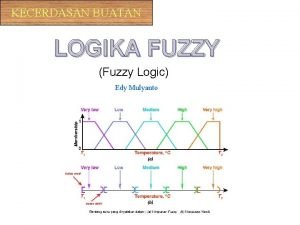
Fuzzy čísla • Nechť a≤b≤c≤d jsou 4 reálná čísla, která splňují: – μA(x)=0 , pro x<a and x>d – μA(x)=1 , pro x mezi b a c – μA(x) je rostoucí mezi a a b. – μA(x) je klesající mezi c a d. • Takovou množinu A nazýváme fuzzy interval. • Pokud b=c nazýváme tuto množinu fuzzy číslo.

Příklad • Velký člověk je vysoký 190 cm +- 20 cm, charakteristická funkce tohoto pojmu je trojuhelníková • Malý člověk je vysoký 160 cm +- 20 cm, charakteristická funkce tohoto pojmu je trojuhelníková • Jak vysoko může dosáhnout malý člověk na zádech velkého?