Mixing Time Section 3 1 Def Total variation

Mixing Time [Section 3. 1] Def: Total variation distance of distributions ¼ and ¼’ on the same countable set : ||¼-¼’||TV : = ½ !2 |¼(!)-¼’(!)| = max. Aµ |¼(A)-¼’(A) | Def: Fully polynomial approximate sampler (FPAUS): given an input x and a sampling tolerance ±>0, the sampler produces an element from a distribution with total variation distance · ± from the target distribution.

Detailed Balance and Reversibility [Section 3. 3] Lemma 3. 7: Let ( , P) be a MC. If distribution ¼’ on satisfies ¼’(x)P(x, y) = ¼’(y)P(y, x) for every x, y 2 , then ¼’ is a stationary distribution of the MC. Note: the condition from Lemma 3. 7 is known as detailed balance (or time reversibility of the MC).

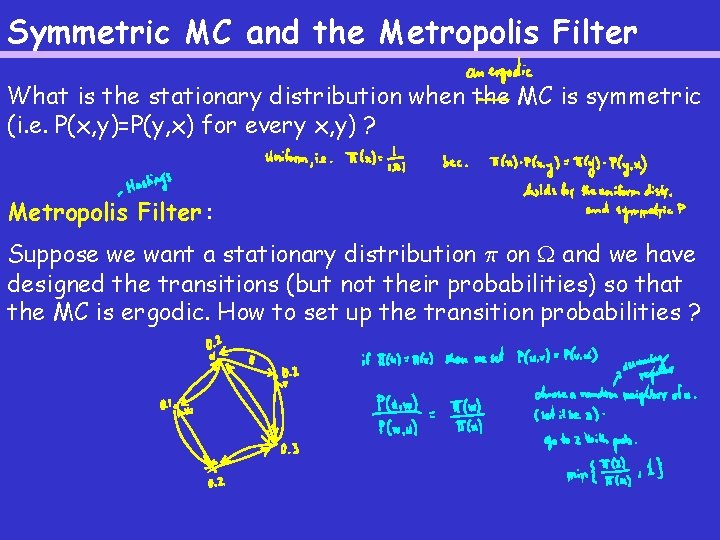
Symmetric MC and the Metropolis Filter What is the stationary distribution when the MC is symmetric (i. e. P(x, y)=P(y, x) for every x, y) ? Metropolis Filter : Suppose we want a stationary distribution ¼ on and we have designed the transitions (but not their probabilities) so that the MC is ergodic. How to set up the transition probabilities ?

Mixing Time cont’ [Chapter 4] Def: Given an ergodic MC ( , P) with stationary distribution ¼, its mixing time from a state x 2 is: ¿x(²) : = min{ t: ||Pt(x, . )-¼||TV · ²}. Overall mixing time is ¿(²) : = maxx 2 ¿x(²). Note: the definition makes sense, i. e. , ||Pt(x, . )-¼||TV is a non-increasing function of t. [Lemma 4. 2]

Coupling [Chapter 4] Recall the MC for colorings: • Choose a vertex v u. a. r. (uniformly at random) • Choose a color c u. a. r. • If none of v’s neighbors is colored by c, recolor v by c. • Otherwise, keep v’s original color. We’ll modify the MC to choose a color not used by any of v’s neighbors. Claim: Let q be the number of colors. If q ¸ M+2, where M is the maximum degree in the graph, then MC is ergodic.

[Chapter 4] Coupling MC for colorings: • Choose a vertex v u. a. r. (uniformly at random) • Choose a color c not used by any neighbor of v u. a. r. • Recolor v by c. Prop. 4. 5: Let G be a graph with max. deg. M. Let the number of colors q ¸ 2 M+1. Then the MC mixes in time: ¿(²) · qn/(q-2 M) ln(n/²).

Coupling [Chapter 4] Coupling idea: - Run two identical MC’s. - They can (and most likely will) be dependent but each without seeing the other MC follows the prescribed transition probabilities. - Start the first MC in the stationary distribution, the other MC starts anywhere. - Goal: the MC’s coalesce, thus the second MC is also following the stationary distribution. - Want to set up the dependence between the MC’s so that they agree with each other more and more as time progresses.

[Chapter 4] Coupling, formally: Given a MC ( , P). A MC on x is a coupling for the above MC if it goes through states (X 0, Y 0), (X 1, Y 1), (X 2, Y 2), … such that: Pr[Xi+1=x’ | Xi=x, Yi=y] = Pr[Yi+1=y’ | Xi-x, Yi=y] =

Coupling [Chapter 4] Warmup: MC on the n-dimensional hypercube (i. e. , binary numbers of length n): - With probability ½ do not do anything. - Otherwise, choose a random position i and flip the i-th bit. Coupling:

[Chapter 4] Coupling Lemma 4. 7 [Coupling Lemma]: Suppose we have a MC with transition matrix P. Let (Xt, Yt) be a coupling of this MC and suppose t: [0, 1] N is a fnc such that Pr[Xt(²) Yt(²) | X 0=x, Y 0=y] · ². Then, the mixing time of the MC: ¿(²) · t(²).

Coupling Back to colorings – how to couple ? [Chapter 4]

Coupling Back to colorings – notation: [Chapter 4]

Coupling Back to colorings – notation: [Chapter 4]

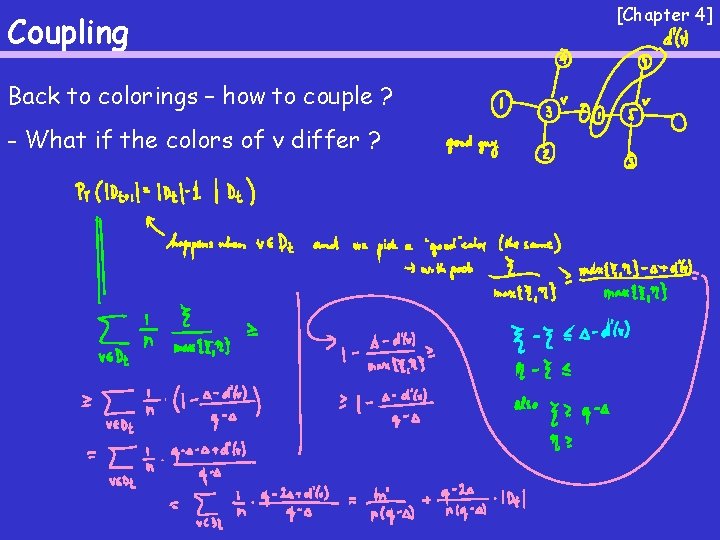
Coupling Back to colorings – how to couple ? - What if the colors of v differ ? [Chapter 4]

Coupling Back to colorings – how to couple ? -What if the colors of v agree ? [Chapter 4]

Coupling Back to colorings – finishing the argument [Chapter 4]

Some useful inequalities Markov’s: If X is a non-negative random variable and a>0, then Pr(X>a) · E(X)/a Chebyshev’s: For any a>0: Pr(|X-E(X)|¸ a) · Var(X)/a 2 No name: 1+x · ex

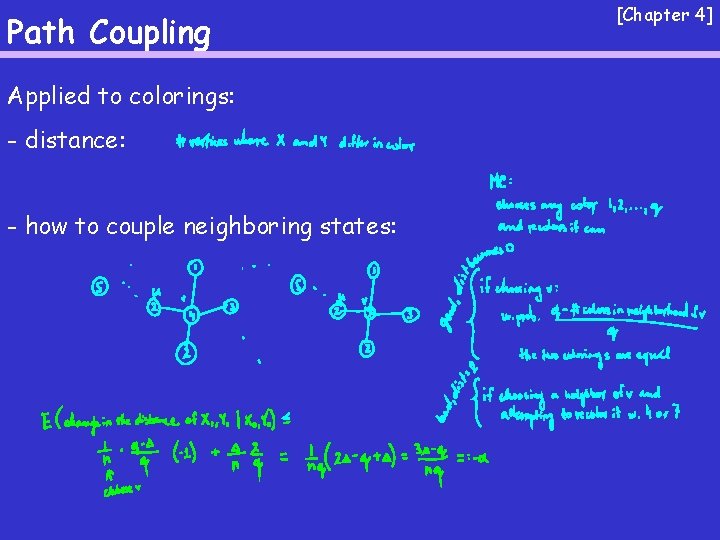
Path Coupling [Chapter 4] - simplifies the coupling analysis Idea: - define distance between states - if neighboring states get closer in one step (in expectation), then all pairs of states get closer in one step - therefore, we have a coupling

Path Coupling Applied to colorings: - distance: - how to couple neighboring states: [Chapter 4]

[Chapter 4] Path Coupling Now in the math-language (drawing from Lemmas 4. 14 -6): Lemma: Suppose for every pair of adjacent states X 0, Y 0: E[distance(X 1, Y 1) | X 0, Y 0] · (1 -®)distance(X 0, Y 0) Then, ¿(²) · ®-1 ln(maxdist/²) where maxdist is the maximum distance between any two states.