MIXING MODELS AND ENDMEMBER MIXING ANALYSIS PRINCIPLES AND

MIXING MODELS AND END-MEMBER MIXING ANALYSIS: PRINCIPLES AND EXAMPLES Matt Miller and Nick Sisolak Slides Contributed by: Mark Williams and Fengjing Liu

OUTLINE ¡ OVERVIEW OF MIXING MODEL ¡ OVERVIEW OF END-MEMBER MIXING ANALYSIS (EMMA) -- PRINCIPAL COMPONENT ANALYSIS (PCA) -- STEPS TO PERFORM EMMA ¡ APPLICATIONS OF MIXING MODEL AND EMMA -- Panola Mountain Research Watershed (Burns et al. , 2001) -- Green Lakes Valley (Liu et al. , 2004)

PART 1: OVERVIEW OF MIXING MODEL ¡ Definition of Hydrologic Flowpaths ¡ 2 -Component Mixing Model ¡ 3 -Component Mixing Model ¡ Generalization of Mixing Model ¡ Geometrical Definition of Mixing Model ¡ Assumptions of Mixing Model
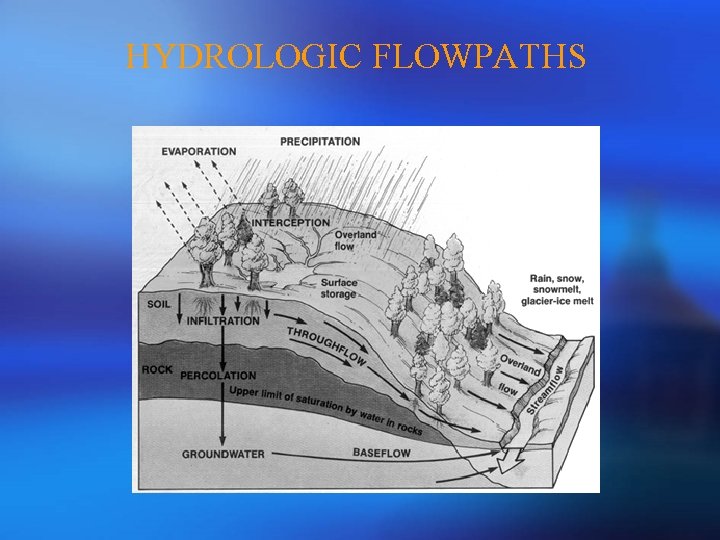
HYDROLOGIC FLOWPATHS

MIXING MODEL: 2 COMPONENTS • One Conservative Tracer • Mass Balance Equations for Water and Tracer

MIXING MODEL: 3 COMPONENTS (Using Specific Discharge) Simultaneous Equations Solutions • Two Conservative Tracers • Mass Balance Equations for Water and Tracers Q - Discharge C - Tracer Concentration Subscripts - # Components Superscripts - # Tracers

MIXING MODEL: 3 COMPONENTS (Using Discharge Fractions) Simultaneous Equations Solutions • Two Conservative Tracers • Mass Balance Equations for Water and Tracers f - Discharge Fraction C - Tracer Concentration Subscripts - # Components Superscripts - # Tracers

MIXING MODEL: Generalization Using Matrices • One tracer for 2 components and two tracers for 3 components • N tracers for N+1 components? -- Yes • However, solutions would be too difficult for more than 3 components • So, matrix operation is necessary Simultaneous Equations Where Solutions Note: • Cx-1 is the inverse matrix of Cx • This procedure can be generalized to N tracers for N+1 components

MIXING MODEL: Geometrical Perspective • For a 2 -tracer 3 -component model, for instance, the mixing subspaces are defined by two tracers. • If plotted, the 3 components should be vertices of a triangle and all streamflow samples should be bound by the triangle. • If not well bound, either tracers are not conservative or components are not well characterized. • fx can be sought geometrically, but more difficult than algebraically.

ASSUMPTIONS FOR MIXING MODEL ¡ Tracers are conservative (no chemical reactions); ¡ All components have significantly different concentrations for at least one tracer; ¡ Tracer concentrations in all components are temporally constant or their variations are known; ¡ Tracer concentrations in all components are spatially constant or treated as different components; ¡ Unmeasured components have same tracer concentrations or don’t contribute significantly.

A QUESTION TO THINK ABOUT ¡ What if we have the number of conservative tracers much more than the number of components we seek for, say, 6 tracers for 3 components? ¡ For this case, it is called over-determined situation ¡ The solution to this case is EMMA, which follows the same principle as mixing models.

PART 2: EMMA AND PCA ¡ EMMA Notation ¡ Over-Determined Situation ¡ Orthogonal Projection ¡ Notation of Mixing Spaces ¡ Steps to Perform EMMA

DEFINITION OF END-MEMBER ¡ For EMMA, we use end-members instead of components to describe water contributing to stream from various compartments and geographic areas ¡ End-members are components that have more extreme solute concentrations than streamflow [Christophersen and Hooper, 1992]

EMMA NOTATION (1) ¡ Hydrograph separations using multiple tracers simultaneously; ¡ Use more tracers than necessary to test consistency of tracers; ¡ Typically use solutes as tracers Modified from Hooper, 2001

EMMA NOTATION (2) ¡ Measure p solutes; p= # of solutes ¡ Assume that there are k linearly independent endmembers (k < p) k = # of end-members ¡ B, matrix of end-members, (k p); each row bj (1 p) ¡ X, matrix of streamflow samples, (n p); each row xi (1 p)

PROBLEM STATEMENT ¡ Find a vector fi of mixing proportions such that Stream chemistry can be defined as a function of end-member contribution ¡ Note that this equation is the same as generalized one for mixing model; the resymbolizing is for simplification and consistency with EMMA references

SOLUTION FOR OVERDETERMINED EQUATIONS ¡ Must choose objective function: minimize sum of squared error ¡ Solution is normal equation [Christophersen et al. , 1990; Hooper et al. , 1990]: ¡ Constraint: all proportions must sum to 1 ¡ Solutions may be > 1 or < 0; this issue will be elaborated later

ORTHOGONAL PROJECTIONS ¡ Following the normal equation, the predicted streamflow chemistry is [Christophersen and Hooper, 1992]: ¡ Geometrically, this is the orthogonal projection of xi into the subspace defined by B, the endmembers

This slide is from Hooper, 2001

OUR GOALS ACHIEVED SO FAR? • We measure chemistry of streamflow and end-members. • Then, we can derive fractions of end-members contributing to streamflow using equations above. • So, our goals achieved? • Not quite, because we also want to test end-members as well as mixing model. • We need to define the geometry of the solute “cloud” (S -space) and project end-members into U-space! • How? Use PCA to determine number and orientation of axes in U-space. Modified from Hooper, 2001

EMMA PROCEDURES • Identification of Conservative Tracers - Bivariate solute-solute plots to screen data; • PCA Performance - Derive eigenvalues and eigenvectors; • Orthogonal Projection - Use eigenvectors to project chemistry of streamflow and end-members; • Screen End-Members - Calculate Euclidean distance of endmembers between their original values and S-space projections; • Hydrograph Separation - Use orthogonal projections and generalized equations for mixing model to get solutions! • Validation of Mixing Model - Predict streamflow chemistry using results of hydrograph separation and original end-member concentrations.

STEP 1 MIXING DIAGRAMS • Look familiar? • This is the same diagram used for geometrical definition of mixing model (components changed to end-members); • Generate all plots for all pair-wise combinations of tracers; • The simple rule to identify conservative tracers is to see if streamflow samples can be bound by a polygon formed by potential end-members or scatter around a line defined by two end-members; • Be aware of outliers and curvature which may indicate chemical reactions!

STEP 2 - PCA PERFORMANCE • For most cases, if not all, we should use correlation matrix rather than covariance matrix of conservative solutes in streamflow to derive eigenvalues and eigenvectors; • Why? This treats each variable equally important and unitless; • How? Standardize the original data set using a routine software or minus mean and then divided by standard deviation; • To make sure if you are doing right, the mean should be zero and variance should be 1 after standardized!

APPLICATION OF EIGENVALUES • Eigenvalues can be used to infer the number of end-members that should be used in EMMA. How? • Sum up all eigenvalues; • Calculate percentage of each eigenvalue in the total eigenvalue; • The percentage should decrease from PCA component 1 to p (remember p is the number of solutes used in PCA); • How many eigenvalues can be added up to 90% (somewhat subjective! No objective criteria for this!)? Let this number be m, m = # of PCA components retained (explains 90% of variance) (m +1) = # of end-members we use in EMMA.

STEP 3 - ORTHOGONAL PROJECTION • X - Standardized data set of streamflow, (n p); • V - Eigenvectors from PCA, (m p); Remember only the first m eigenvectors to be used here! Project End-Members • Use the same equation above; • Now X represents a vector (1 p) for each end-member; • Remember X here should be standardized by subtracting streamflow mean and dividing by streamflow standard deviation!

STEP 4 - SCREEN END-MEMEBRS Geometrically • Plot a scatter plot for streamflow samples and end-members using the first and second PCA projections; • Eligible end-members should be vertices of a polygon (a line if m = 1, a triangle if m = 2, and a quadrilateral if m = 3) and should bind streamflow samples in a convex sense; Algebraically • Calculate the Euclidean distance between original chemistry and projections for each solute using the equations below: • j represent each solute and bj is the original solute value Those steps should lead to identification of eligible end-members!
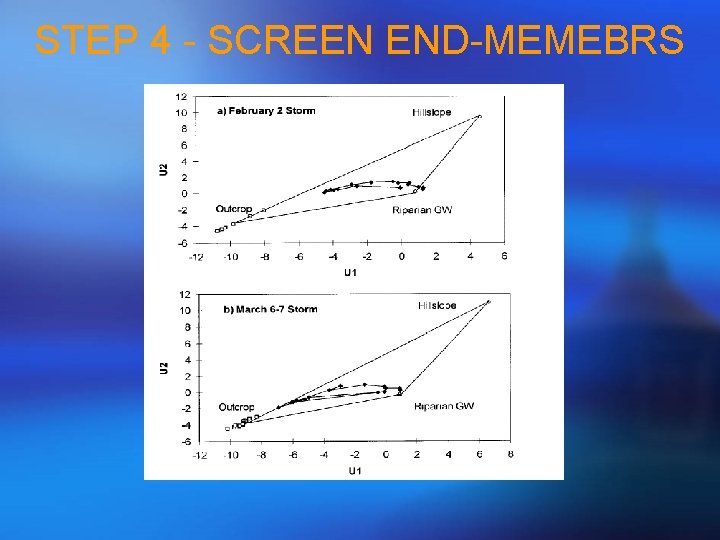
STEP 4 - SCREEN END-MEMEBRS

STEP 5 - HYDROGRAPH SEPARATION • Use the retained PCA projections from streamflow and endmembers to derive flowpath solutions! • So, mathematically, this is the same as a general mixing model rather than the over-determined situation. Solve for Q’s

STEP 6 - PREDICTION OF STREAMFLOW CHEMISTRY • Multiply results of hydrograph separation (usually fractions) by original solute concentrations of end-members to reproduce streamflow chemistry for conservative solutes; • Comparison of the prediction with the observation can lead to a test of mixing model.


PROBLEM ON OUTLIERS • PCA is very sensitive to outliers; • If any outliers are found in the mixing diagrams of PCA projections, check if there are physical reasons; • Outliers have negative or > 1 fractions; • See next slide how to resolve outliers using a geometrical approach for an end-member model.

RESOLVING OUTLIERS • A, B, and C are 3 endmembers; • D is an outlier of streamflow sample; • E is the projected point of D to line AB; • a, b, d, x, and y represent distance of two points; • We will use Pythagorean theorem to resolve it. • The basic rule is to force fc = 0, f. A and f. B are calculated below [Liu et al. , 2003]:

SUMMARY: EMMA ¡ IDENTIFY MULTIPLE SOURCE WATERS AND FLOWPATHS ¡ QUANTITATIVELY SELECTS NUMBER AND TYPE OF END-MEMBERS ¡ QUANTITATIVELY EVALUATE RESULTS ¡ IDENTIFY MISSING END-MEMBERS

Burns et al. (2001)

Objectives ¡ Use EMMA to derive three-component model during 2 rain storms to answer: 1) What is the relative importance of each end -member to stream runoff? 2)How do runoff processes vary with storm size, rain intensity, and antecedent wetness conditions? 3)Are EMMA modeling results consistent with physical hydrologic measurements?

Site Description ¡ Study Site: PMRW ¡ 10 ha ¡ 3 assumed End-members: 1)Outcrop 2) Hillslope 3)Riparian Area

Field Methods ¡ Chemical Analysis 1) 2) 3) 4) Stream water Runoff from outcrop Subsurface stormflow from hillslope trench Riparian ground water ¡ Physical Meaurements 1) 2) 3) 4) Stream runoff rate Rainfall amount/intensity Runoff rate from hillslope trench Riparian water table levels

EMMA Modeling 1) 2) 3) 4) 5) 6) Five solutes used as tracers Data Standardized into correlation matrix PCA Concentrations of end-members projected into U -space Examine extent to which end-members bound stream water observations in U-space. Solute concentrations predicted by EMMA compared with measured concentrations during 2 storms

Storm Characteristics
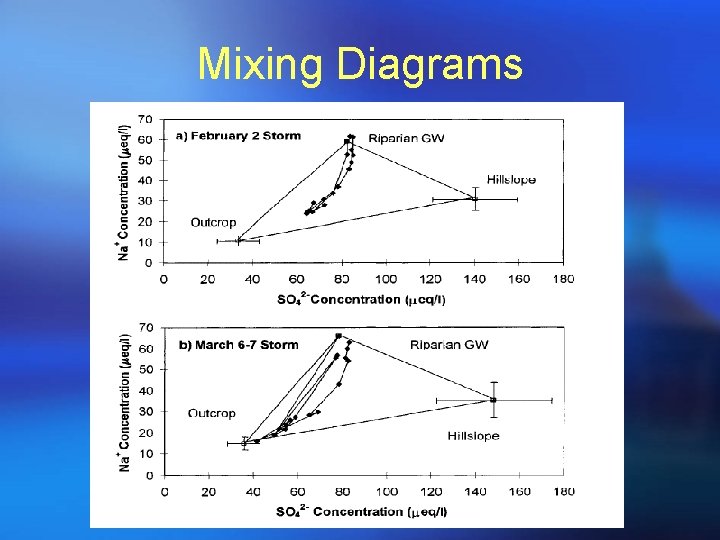
Mixing Diagrams
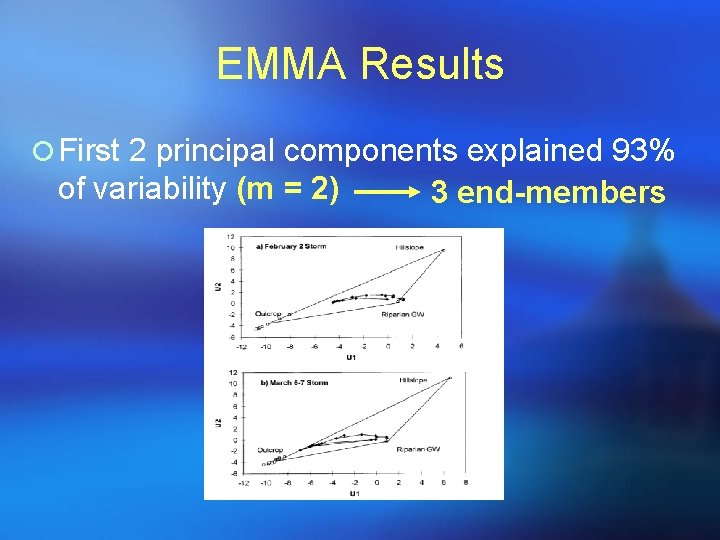
EMMA Results ¡ First 2 principal components explained 93% of variability (m = 2) 3 end-members

End-member contributions
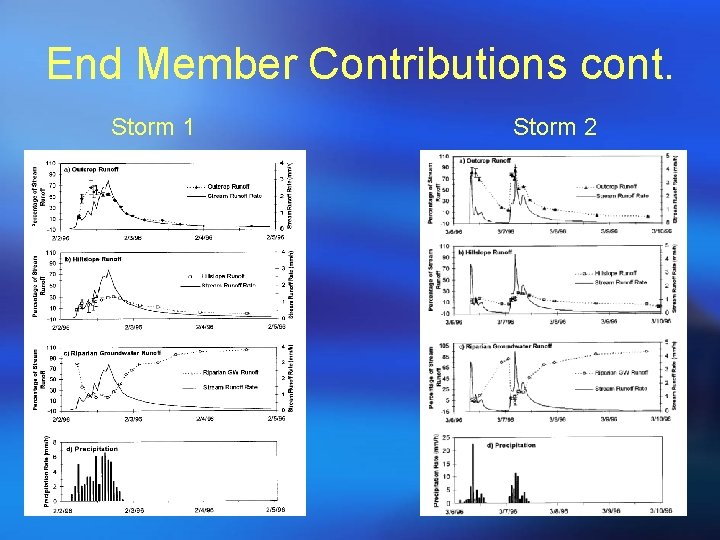
End Member Contributions cont. Storm 1 Storm 2

Test of Mixing Model ¡ Using fraction of Flow from EMMA (fo, fh, and fr) with measured end-member concentrations calculate predicted stream flow concentrations. ¡ Linear Regression of Predicted vs. Measured Concentrations… r^2 = 0. 95 -0. 99
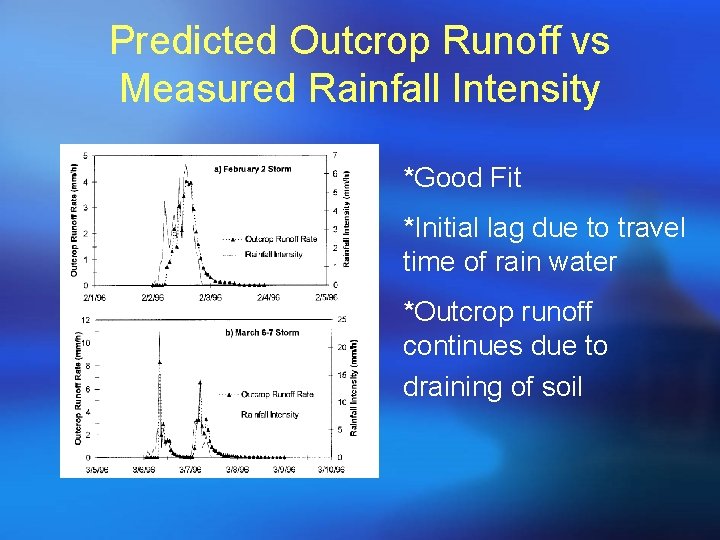
Predicted Outcrop Runoff vs Measured Rainfall Intensity *Good Fit *Initial lag due to travel time of rain water *Outcrop runoff continues due to draining of soil

Predicted Hillslope Runoff and Measured Trench Outflow *Hillslope trench located halfway up hillslope *Lower soil moisture before March Storm *Subsurface storm flow likely provided recharge to riparian ground water and dry hillslope soils.
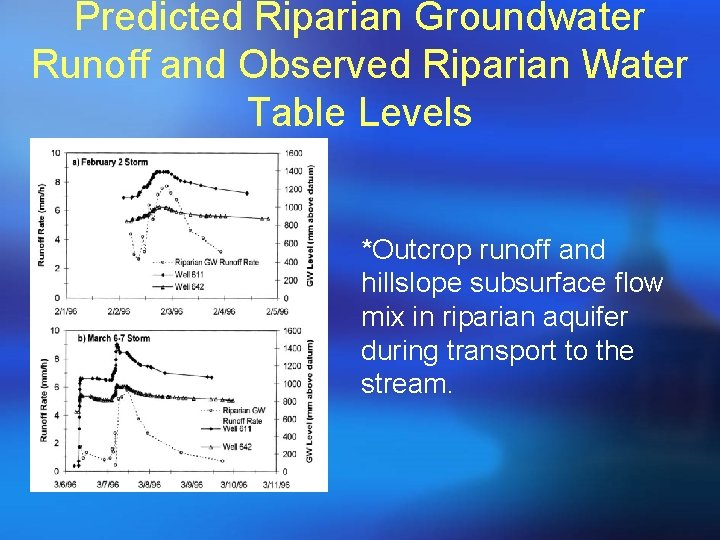
Predicted Riparian Groundwater Runoff and Observed Riparian Water Table Levels *Outcrop runoff and hillslope subsurface flow mix in riparian aquifer during transport to the stream.
- Slides: 47