Mixed Strategies What is a mixed strategy A

Mixed Strategies

What is a mixed strategy? • A player chooses to ``randomize’’ between ``pure strategies’’, assigning a specific probability to taking each possible pure strategy. • If the other player knows your strategy, when would you want it to be a mixed strategy with non-zero probabilities of more than one action?

Matching Pennies: or Simple hide and seek_ Player 2 (Seeker) q Heads p Player 1 (Hider) 1 -p Tails Heads 1 -q Tails -1, 1 1, -1 -1, 1

The game of matching pennies has A) two pure strategy Nash equilibria B) One pure strategy Nash equilibrium C) One mixed strategy Nash equilibrium and no pure strategy Nash equilibria D) Two mixed strategy Nash equilibria and no pure strategy Nash equilibria E) One mixed strategy Nash equilibrium and two pure strategy Nash equilibria.

Nash equilibrium in Matching Pennies Suppose Player 1 randomizes and plays Heads 2/3 of the time, what is Player 2’s best response? A) Heads for sure B) Tails for sure C) Randomize with Probability of Heads 2/3. D) Randomize with Probability of Tails 2/3

Best response Mapping Player 2’s Reaction Function (in Red) 1 q=probability 2 chooses H Player 1’s Reaction Function (in Green) 1/2 0 1/2 1 p= Probability 1 chooses H

Nash equilibrium in Mixed Strategies • Intersection of Reaction Functions • Each is doing best response to other’s strategy

A Fundamental Theorem • Some games have no equilibrium in pure strategies: Examples: matching pennies; rock, paper scissors • Every game in which there is a finite number of pure strategies has at least one mixed strategy equilibrium.

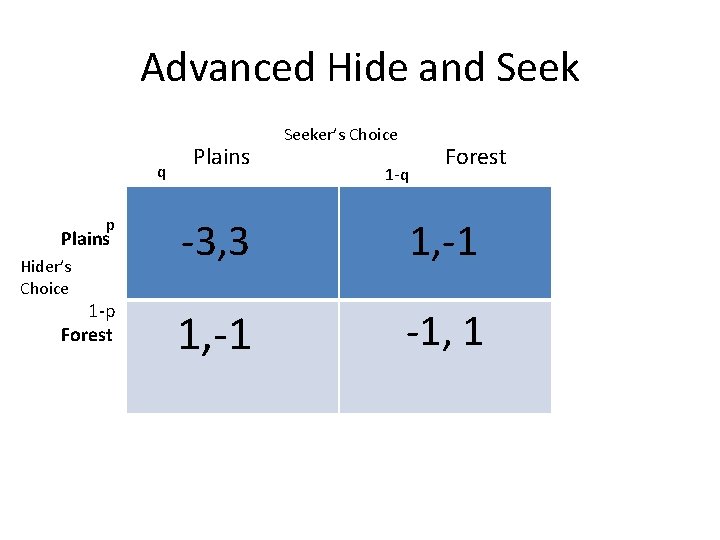
Advanced Hide and Seek q Plains Seeker’s Choice 1 -q Forest p -3, 3 1, -1 1 -p Forest 1, -1 -1, 1 Plains Hider’s Choice

Mixed strategy equilibrium • In a mixed strategy equilibrium, all strategies that are assigned positive probability have equal expected value. • You can use this fact to find mixed strategy Nash equilibria.

Example: Advanced Hide and Seek • When does Seeker have a mixed strategy best response. The payoffs to looking in the plains and looking in the forest must be the same. • Where p is probability Hider is in the plains, • Payoff to Plains is p 3+(1 -p)(-1)=4 p-1. • Payoff to Forest is -1 p +(1 -p)1=1 -2 p • 4 p-1=1 -2 p if and only if 6 p=2, p=1/3.

Best response Mapping 1 q=probability Player 1’s 2 chooses Plains Reaction Player 2’s Reaction Function (in Red) Function (in Green) 1/3 0 1/3 1 p= Probability 1 chooses Plains

Expected Utility Theory of Choice Under Uncertainty • Suppose that you face random outcomes. You assign a “utility” to each possible outcome in such a way that your choices among uncertain prospects are those that maximize “expected utility”.

Expected utility Example: Utility of money • Suppose you have a lottery that will with probability 1/4 win 10 million dollars and with probability ¾ will be worthless. You get just one chance to sell your ticket. Would you sell it for 2. 5 million dollars? A) Yes B) No

Expected utility Example: Utility of money • Suppose you have a lottery that will with probability 1/4 win 10 million dollars and with probability ¾ will be worthless. You get just one chance to sell your ticket. Would you sell it for 1 million dollars? A) Yes B) No

Expected utility Example: Utility of money • Suppose you have a lottery that will with probability 1/4 win 100 million dollars and with probability ¾ will be worthless. You get just one chance to sell your ticket. Would you sell it for 500 thousand dollars? A) Yes B) No

Construct a utility scale • Let u(10 million)=1 Let u(0)=0. • Then ask question. How much money X for sure would be just as good as having a ¼ chance of winning 10 million and ¾ chance of 0? • Then assign u(X)=(3/4)u(0)+(1/4)u(10, 000)= (3/4)0+(1/4)1=1/4.

Assigning utility to any income • Lets choose a scale where u(0)=0 and u(10 million)=1. • Take any number X. Find a probability p(X) so that you would just be willing to pay $X for a lottery ticket that pays 10 million with probability p(X) and 0 with probability 1 -p(x). • Assign utility p(X) to having $X.

Field Goal or Touchdown? • Field goal is worth 3 points. • Touchdown is worth 7 points. Which is better? Sure field goal or probability ½ of touchdown?

Finding the coach’s von Neumann Morgenstern utilities • Set utility of touchdown u(T)=1 • Set utility no score u(0)=0 The utility of a gamble in which you get a touchdown with probability p and no score with probability 1 -p is pu(T)+(1 -p)u(0). What utility u(F) to assign to a sure field goal? Let p* be the probability such that the coach is indifferent between scoring a touchdown with probability p* (with no score with prob 1 -p*) and having a sure field goal. Then u(F)=p*u(T)+(1 -p*)u(0)=p*x 1+(1 -p*)x 0=p*.

Volunteers’ Dilemma N people observe a mugging. Someone needs to call the police. Only one call is needed. Cost of calling is c. Cost of knowing that the person is not helped is T. Should you call or not call? T>c>0. Many asymmetric pure strategy equilibria. Also one symmetric mixed strategy equilibrium.

Mixed strategy equilibrium • Suppose everybody uses a mixed strategy with probability p of calling. • In equilibrium, everyone is indifferent about calling or not calling if expected cost from not calling equals cost from calling. Expected Cost of of not calling is T(1 -p)N-1 • Expected cost of calling is c. • Equilibrium has c= T(1 -p)N-1 so 1 -p=(c/T)1/N-1 • Then (1 -p)N=(c/T)N/N-1 is the probability that nobody calls. This is an increasing function of N. So the more People who observe, the less likely that someone calls.

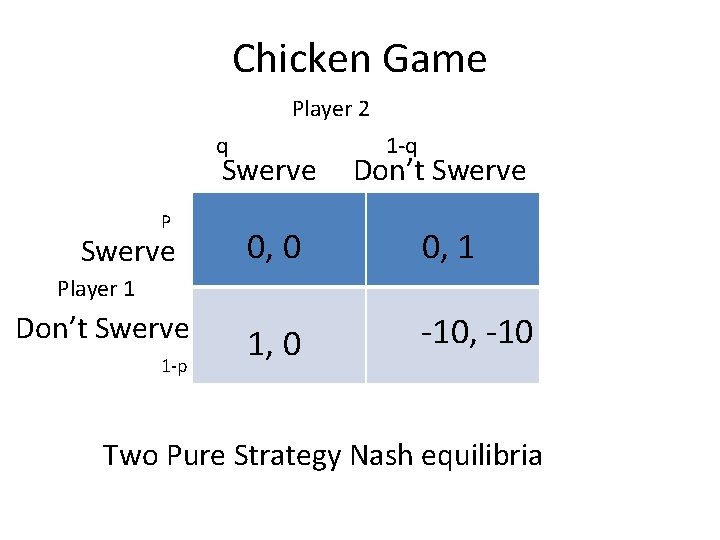
Chicken Game Player 2 q P Swerve 1 -q Swerve Don’t Swerve 0, 0 0, 1 1, 0 -10, -10 Player 1 Don’t Swerve 1 -p Two Pure Strategy Nash equilibria

Mixed Strategy When is Player 1 indifferent between the two strategies, Swerve and Don’t Swerve? Expected payoff from Swerve is 0. Expected payoff from Don’t Swerve is q-10(1 -q). So Player 1 will use a mixed strategy best response only if 0=11 q-10 or q=10/11. Similar reasoning inplies that in Nash equilibrium p=10/11. Crash occurs with probability 1/121.

Battle of Sexes Movie A Alice Movie B BRA(A)=A BRA(B)=B Bob Movie B 3, 2 1, 1 0, 0 2, 3 BRB(A)=A BRB(B)=B

Mixed Strategy Equilibrium • Let p be probability Alice goes to movie A and q the probability that Bob goes to movie B. • When is there a mixed best response for Alice? – Expected payoff for Movie A for Alice is 3(1 -q)+ q 1=3 -2 q. – Expected payoff to Movie B for Alice is 2 q+(1 -q)0=2 q • Payoffs are the same if 3 -2 q= 2 q, so q=3/4.

Similar for Bob • From the symmetry of the game, we see that a mixed strategy is a best response for Bob if p=3/4. • In a symmetric mixed strategy, each goes to his or her favorite movie with probability ¾. • Probability that they get together at Movie A is 3/4 x 1/4=3/16. Probability that they get together at Movie B is also 3/16. Probability that they miss each other is 5/8. Probability that each goes to favorite movie is 9/16. Probability that they each go to less preferred movie is 1/16.

Have a nice weekend!