Mixed Linear Models An Introductory Tutorial Mixed Models

Mixed Linear Models An Introductory Tutorial

Mixed Models in Context Other options for longitudinal n n n Repeated Measures ANOVA MANOVA GEE (we won’t talk about this) Univariate analysis of Longitudinal Data n n ANCOVA Change score

Drop out and You Drop out is a reality in any study, and so far we have ignored it. Drop out creates missing values in a subjects data. Some data analysis methods deal with this better than others Why do subjects drop out n Missing Completely At Random: MCAR w Drop out is completely unrelated to the outcomes of interest w e. g. Poor record keeping, Forgot to administer the measure, Moving n Missing At Random: MAR w Drop out is related to the observed outcomes w e. g. Subjects with a poor outcome at baseline tend to drop out n Missing Not At Random: MNAR w Drop out is related to unobserved outcomes (Bad news for the data analyst) w e. g. Subjects whose outcome decreases after a visit are less likely to come in for the next one Mixed models are okay if the drop out is either MCAR or MAR

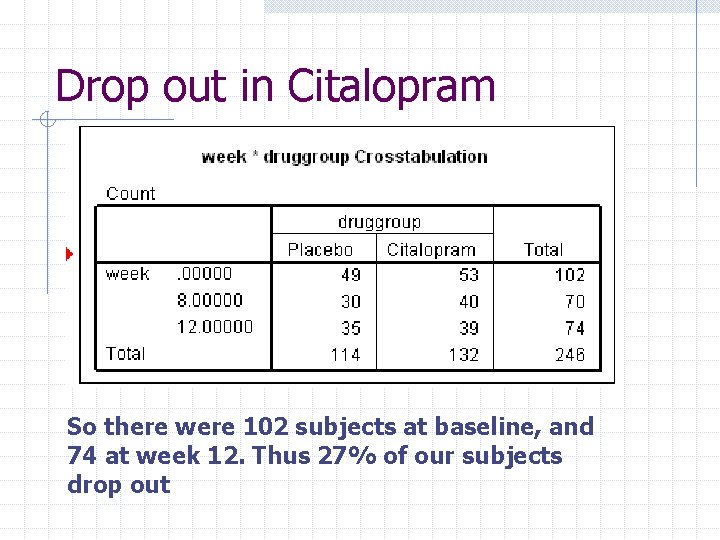
Drop out in Citalopram So there were 102 subjects at baseline, and 74 at week 12. Thus 27% of our subjects drop out

Repeated Measures ANOVA (r. ANOVA) A group by time r. ANOVA is similar to our random intercept model. n Time is treated as a factor (I. e. dummy coded) n Hypotheses that can be tested are: w Different treatment progressions w Pair wise comparisons / endpoint / change from baseline n Sphericity (Compound Symmetry) is assumed w All time points have equal correlation to all other time points (slightly more complicated, but essentially this) n Missing completely at random is assumed w Each subject must be observed at all time points to be included in analysis. n Option 1: Analyze only the complete cases n Option 2: Impute values into the missing time points (e. g. Last Observation carried forward (LOCF)

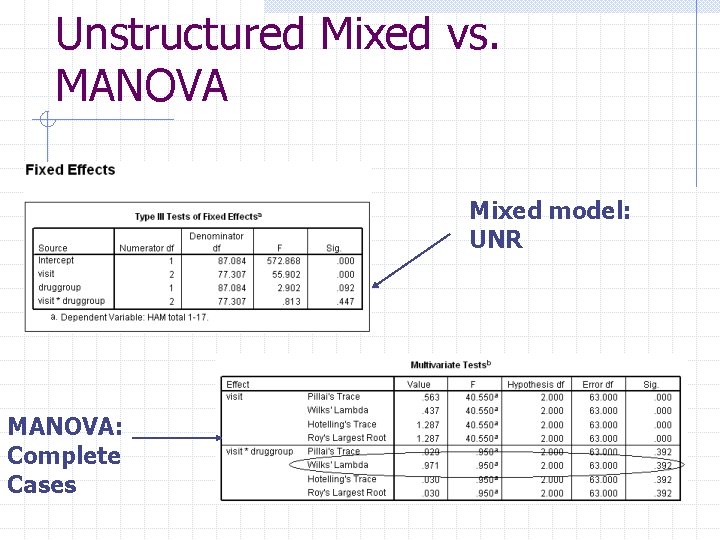
MANOVA A MANOVA is similar to a treatment by time mixed model with unstructured covariance n n Time is treated as a factor (i. e. dummy coded) Hypotheses that can be tested are: w Different treatment progressions n Missing completely at random is assumed w Each subject must be observed at all time points to be included in analysis. n n Option 1: Analyze only the complete cases Option 2: Impute values into the missing time points (e. g. Last Observation carried forward (LOCF)

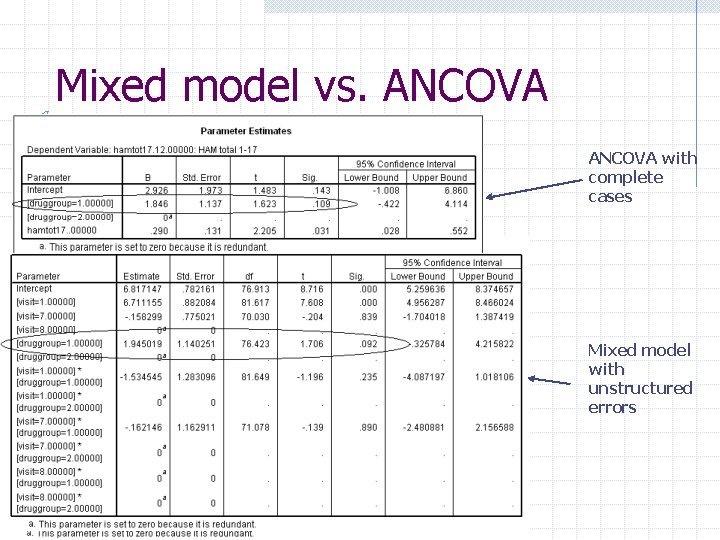
ANCOVA Analysis of the last observation n n Covariate on the baseline observation to increase precision Hypothesis tested is: w Are subjects different at the last time point n Missing completely at random is assumed w Each subject must be observed at all time points to be included in analysis. n n Option 1: Analyze only the subjects that make it to the end Option 2: Analyze the last observed time point for each subject

Change score Analysis of the change score (Y at endpoint – Y at baseline) n n t-test of the change scores Hypothesis tested is: w Are subjects different at the last time point n Missing completely at random is assumed w Each subject must be observed at all time points to be included in analysis. n n Option 1: Analyze only the subjects that make it to the end Option 2: Analyze the last observed time point for each subject as the endpoint

Random Intercept Mixed model vs. r. ANOVA HAM: 3 time points. Treatment vs placebo Random intercept MM r. ANOVA: Complete cases

Unstructured Mixed vs. MANOVA Mixed model: UNR MANOVA: Complete Cases

Mixed model vs. ANCOVA with complete cases Mixed model with unstructured errors

Change Score Mixed Model t-test