MITM 613 Intelligent System Chapter 9 Hybrid Systems

MITM 613 Intelligent System Chapter 9: Hybrid Systems Abdul Rahim Ahmad

2 Chapter Nine: Hybrid Systems 9. 1 9. 3 9. 4 9. 5 Abdul Rahim Ahmad Convergence of techniques Genetic-fuzzy systems Neuro-fuzzy systems Genetic-neural systems

3 Convergence of techniques § Many computing techniques can be applied to particular problems: § symbolic representations (eg. knowledge-based systems) § computational intelligence § conventional programs § They are not exclusive alternatives but complementary to each other and can be made into hybrid of mixed techniques. Abdul Rahim Ahmad

4 Convergence of techniques § How different computational techniques can be complementary? § When dealing with multifaceted problems § For Capability enhancement § For Cases where parameter settings are needed § For Clarification and verification Abdul Rahim Ahmad

5 Combining Techniques § When Dealing with multifaceted problems § Real life problems are multi facet. § Different specialize module deal with specific task § Modules can communicate between each other (eg: in Black board system) § When Enhancing Capability of a system § A technique A can be used within another technique B to enhance the capabilities of B. Abdul Rahim Ahmad

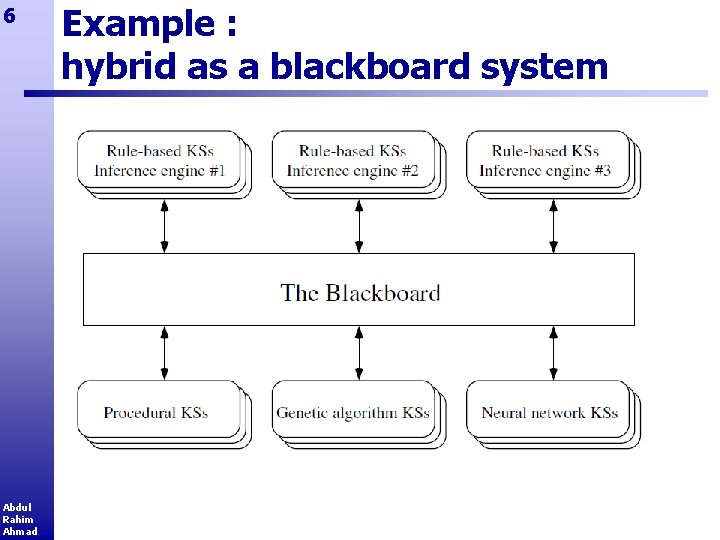
6 Abdul Rahim Ahmad Example : hybrid as a blackboard system

7 Combining Techniques § When Setting Parameters § Use one technique to set the parameters of another technique. § Eg: neuro-fuzzy, genetic-neural. § When Performing Clarification and verification (In Neural network) § Hybrid method used to find the reasons of associations bet. input and output and the weights. § To automatically extract from the network, rules that can be readily understood, and to write verification rules to check the validity of the network’s output. Abdul Rahim Ahmad

8 9. 2 Blackboard System Abdul Rahim Ahmad

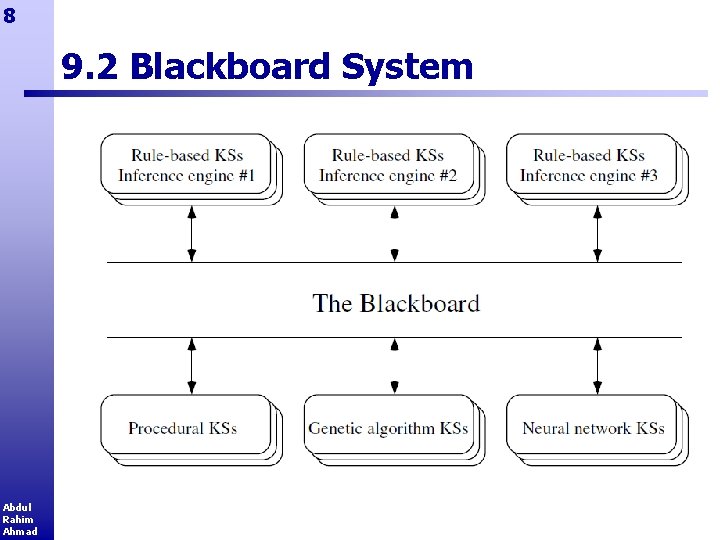
9 Blackboard Model § Blackboard model or blackboard architecture provides a software structure well suited to multifaceted tasks. § Systems that have this kind of structure are called blackboard systems. § In such a system, knowledge of the application domain is divided into modules, referred to as knowledge sources (or KSs), each of which is designed to tackle a particular subtask. § KSs are independent and can communicate only by reading from or writing to the blackboard, a globally accessible working memory where the current state of understanding is represented. § KSs can also delete unwanted information from the blackboard. Abdul Rahim Ahmad

10 Blackboard System § A blackboard system is analogous to a team of experts who communicate their ideas via a physical blackboard, by adding or deleting items in response to the information that they find there. § Each knowledge source represents such an expert having a specialized area of knowledge. § As each KS can be encoded in the most suitable form for its particular task, blackboard systems offer a mechanism for the collaborative use of different computational techniques such as rules, neural networks, and fuzzy logic. Abdul Rahim Ahmad § The inherent modularity of a blackboard system is also helpful for maintenance. Each rule-based knowledge source can use a suitable reasoning strategy for its particular task, e. g. , backward- or forward-chaining, and can be thought of as a rule-based system in microcosm.

11 Blackboard System Abdul Rahim Ahmad § Knowledge sources are applied in response to information on the blackboard, when they have some contribution to make. This leads to increased efficiency since the detailed knowledge within a knowledge source is only applied when that knowledge source becomes relevant. § In the idealized blackboard system, the KSs are said to be opportunistic, activating themselves whenever they can contribute to the global solution. § However, this is difficult to achieve in practice as it may involve interrupting another knowledge source that is currently active. § One approach to KS scheduling is to use a control module that determines the order of KS activation on the basis of applicability and past use of the KSs. § As an extension of this idea, a separate blackboard system could select knowledge sources based upon explicit rule-based knowledge of the alternatives. This level of sophistication may, however, result in a slow response.

12 Blackboard System § Some degree of structure is imposed on the blackboard by dividing it into panels. § A knowledge source then only needs to look at a small number of panels rather than the whole blackboard. § Typically the blackboard panels correspond to different levels of analysis of the problem, progressing from detailed information to more abstract concepts. § Examples: § Hearsay-II blackboard system for computerized understanding of natural speech, the levels of analysis include those of syllable, word, and phrase. § Ultrasonic image interpretation using ARBS, the levels progress from raw signal data, via a description of the significant image features, to a description of the defects in the component Abdul Rahim Ahmad

13 Advantages of Blackboard System Abdul Rahim Ahmad § Many and varied sources of knowledge can participate in the development of a solution to a problem. § Each knowledge source has access to the blackboard, so it can be applied as soon as it becomes appropriate. (opportunism, i. e. , application of the right knowledge at the right time). § For problems involving large amounts of numerical processing, the characteristic style of incremental solution development is particularly efficient. § Different types of reasoning strategy (e. g. , data- and goal-driven) can be mixed as appropriate in order to reach a solution. § Hypotheses can be posted onto the blackboard for testing by other knowledge sources. A complete test solution does not have to be built before deciding to modify or abandon the underlying hypothesis. § In the event that the system is unable to arrive at a complete solution to a problem, the partial solutions appearing on the blackboard are available and may be of some value.

14 Genetic-fuzzy systems § Performance of a fuzzy system depends on the definitions of the fuzzy sets and on the fuzzy rules. § As these parameters can all be expressed numerically, it is possible to devise a system whereby they are learned automatically using genetic algorithms (GA). § A chromosome can be devised that represents the complete set of parameters for a given fuzzy system. § The cost function could then be defined as the total error when the fuzzy system is presented with a number of different inputs with known desired outputs. Abdul Rahim Ahmad

15 Genetic-fuzzy systems § Fuzzy rules can be drawn up fairly easily, but defining the most suitable membership functions remains a difficult task. § A scheme by Karr is where all membership functions are triangular. § The variables are constrained to lie within a fixed range, so the fuzzy sets low and high are both right-angle triangles § The slope of these triangles can be altered by moving their intercepts on the abscissa, marked max 1 and min 4. § All intermediate fuzzy sets are assumed to have membership functions that are isosceles triangles. Each is defined by two points, maxi and mini, where i labels the fuzzy set. § The chromosome is then a list of all the points maxi and mini that determine the complete set of membership functions. Abdul Rahim Ahmad

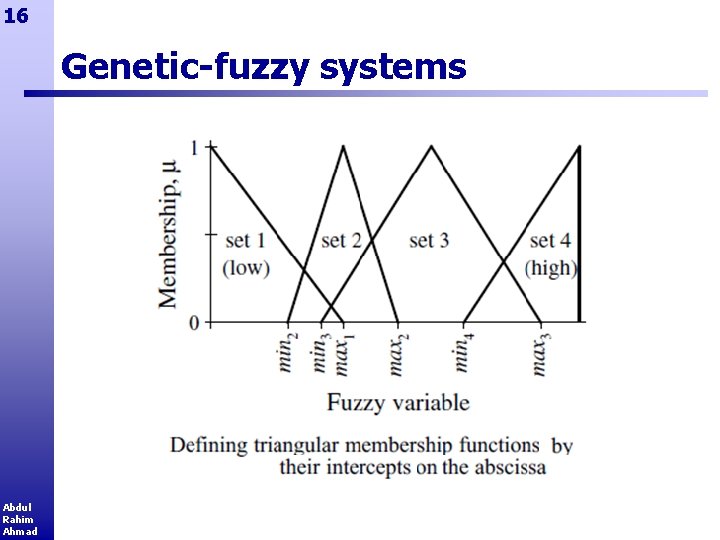
16 Genetic-fuzzy systems Abdul Rahim Ahmad

17 9. 3 Genetic-fuzzy systems § In this scheme, the genetic algorithm for parameter setting and the fuzzy system that uses those parameters are distinct and separate. § The parameters for a fuzzy system can also be learned using neural networks, where there is much closer integration between the neural network and the fuzzy system. Abdul Rahim Ahmad

18 9. 4 Neuro-fuzzy systems § A neuro-fuzzy system is a fuzzy system where the parameters of which are derived by a neural network learning technique. § Can also be viewed as a neural network that represents a fuzzy system. § The two views are equivalent : § possible to express a neuro-fuzzy system in either form. Abdul Rahim Ahmad

19 Example § Consider the following fuzzy rules /* Rule 9. 1 f */ IF temperature is high OR water level is high THEN pressure is high /* Rule 9. 2 f */ IF temperature is medium OR water level is medium THEN pressure is medium /* Rule 9. 3 f */ IF temperature is low OR water level is low THEN pressure is low § These fuzzy rules and the corresponding membership functions can be represented by the neural network on the next page. Abdul Rahim Ahmad

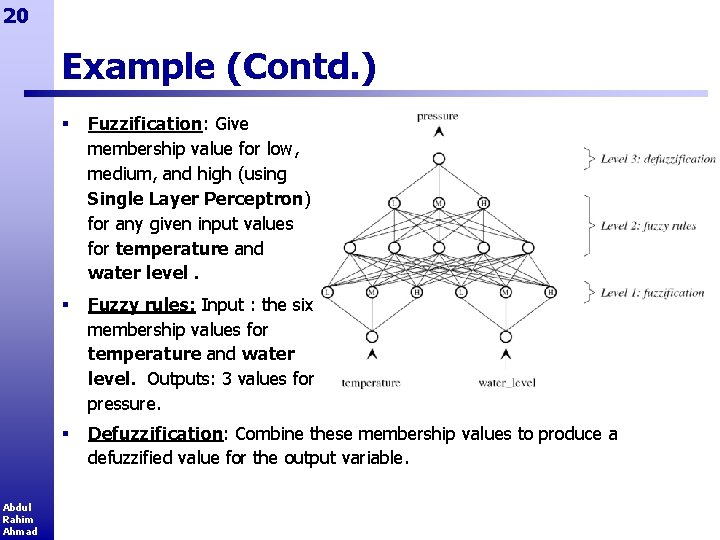
20 Example (Contd. ) Abdul Rahim Ahmad § Fuzzification: Give membership value for low, medium, and high (using Single Layer Perceptron) for any given input values for temperature and water level. § Fuzzy rules: Input : the six membership values for temperature and water level. Outputs: 3 values for pressure. § Defuzzification: Combine these membership values to produce a defuzzified value for the output variable.

21 Example (Contd. ) § The definitions of the fuzzy sets and the fuzzy rules are implicit in the connections and weights of the neuro-fuzzy network. § Using a suitable learning mechanism, the weights can be learned from a series of examples. § The network can then be used on previously unseen inputs to generate defuzzified output values. § In principle, the fuzzy sets and rules can be inferred from the network and run as a fuzzy rule-based system Abdul Rahim Ahmad

22 9. 5 Genetic-neural systems § A challenge in building a neural network is to choose the right architecture and the right learning parameters. § For a NN, a decision needs to be made on : § the learning parameters § the necessary number of neurons § whether additional layers would be beneficial. § It is possible to use a genetic algorithm to optimize the network design. § cost function might combine the RMS error with duration of training. Abdul Rahim Ahmad

23 9. 5 Genetic-neural systems § Supervised training of a NN involves § adjusting its weights until the output patterns obtained for a range of input patterns are close to the desired patterns. § The different network topologies use different training algorithms for achieving this weight adjustment, through back-propagation or errors. § However, it is also possible to use a genetic algorithm to train the network. Abdul Rahim Ahmad

24 9. 5 Genetic-neural systems § In the genetic-neural syatem: § each gene represent a network weight, so that a complete set of network weights is mapped onto an individual chromosome. § Each chromosome can be evaluated by testing a neural network with the corresponding weights against a series of test patterns. Abdul Rahim Ahmad § A fitness value can be assigned according to the error, so that the weights represented by the fittest generated individual correspond to a trained neural network.

25 9. 6 Clarifying and verifying NN § In Neural networks, internals is a “black box” : § Ie: the inputs and outputs are significant to user but the weights is not. § In KBS, the internal state, (eg: value of a variable) does have meaning for the user. § Now, research are done to extract rule which are equivalent to the trained neural network from which they have been extracted including production rules and fuzzy rules. § Example : in safety-critical systems. Abdul Rahim Ahmad

26 Example: Safety-critical Systems § In safety-critical systems, cannot rely on output from a neural network without verification. § Need rules to verify consistency of a neural network output with its input. § Use of rules for verification implies that at least some of the domain knowledge can be expressed in rule form § One suggestion is to use an adjudicator module to decide whether a set of rules or a neural network is likely to provide the more reliable output for a given input. § Adjudicator need access to NN training data and could determine whether a NN would have to interpolate between, or extrapolate from, examples in the training. Abdul Rahim Ahmad

27 Example: Safety-critical Systems § In safety-critical systems, cannot rely on output from a neural network without verification. § Need rules to verify consistency of a neural network output with its input. § Use of rules for verification implies that at least some of the domain knowledge can be expressed in rule form § One suggestion is to use an adjudicator module to decide whether a set of rules or a neural network is likely to provide the more reliable output for a given input. § Adjudicator need access to NN training data and could determine whether a NN would have to interpolate between, or extrapolate from, examples in the training. Abdul Rahim Ahmad

28 Example: Safety-critical Systems § Neural networks are good at interpolation but poor at extrapolation. Thus, the adjudicator may call upon rules to handle the exceptional cases which would otherwise require a neural network to extrapolate from its training data. § If heuristic rules are also available for the less exceptional cases, then they could be used to provide an explanation for the neural network’s findings. § A supervisory rule-based module could dictate the training of a neural network § deciding how many nodes are required Abdul Rahim Ahmad § adjusting the learning rate as training proceeds § deciding when training should terminate.