MISKOLCI EGYETEM GAZDASGTUDOMNYI KAR Idsorok elemzse Dr Varga

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Idősorok elemzése Dr. Varga Beatrix 1

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Idősorok grafikus ábrázolása Grafikus ábrázolás: Az idősorok alaptendenciáinak tömör, áttekintő jellemzése leggyakrabban vonal, vagy oszlopdiagram segítségével történik. Fő típusai: q Állapotidősorok: az időbeli ismérv értékei egy-egy időponthoz tartoznak. Ábrázolásuk különálló oszlopokkal történik. q Tartamidősorok: a vízszintes tengelyen elvben intervallumok szerepelnek, a jelenséget pedig célszerű ezen intervallumok fölé rajzolt oszlopokkal, vagy vonaldiagrammal bemutatni. 2

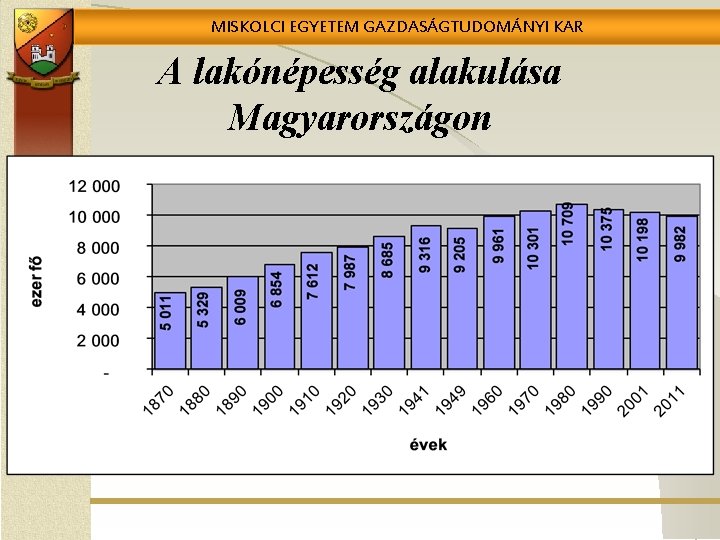
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR A lakónépesség alakulása Magyarországon

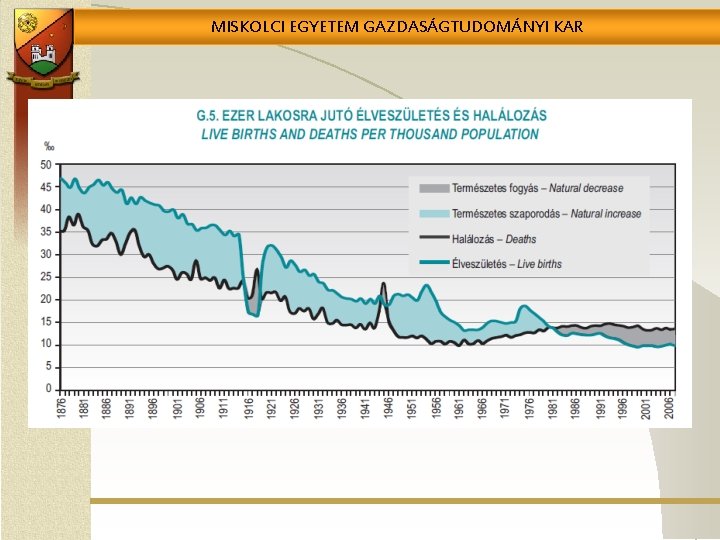
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR

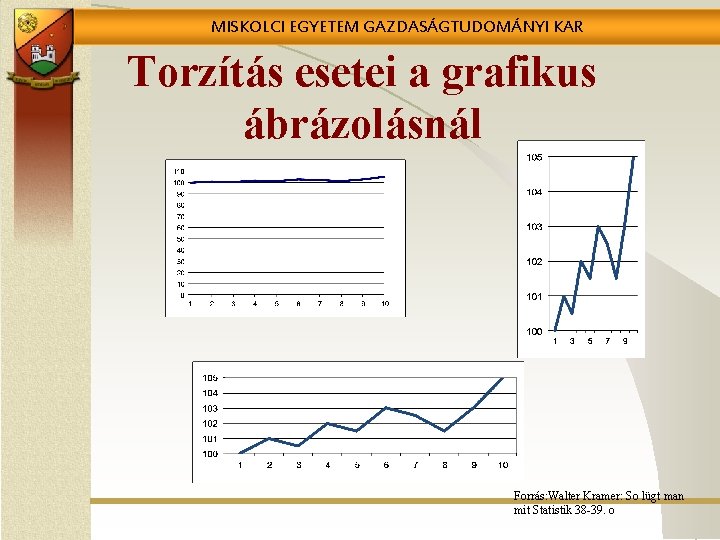
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Torzítás esetei a grafikus ábrázolásnál Forrás: Walter Kramer: So lügt man mit Statistik 38 -39. o

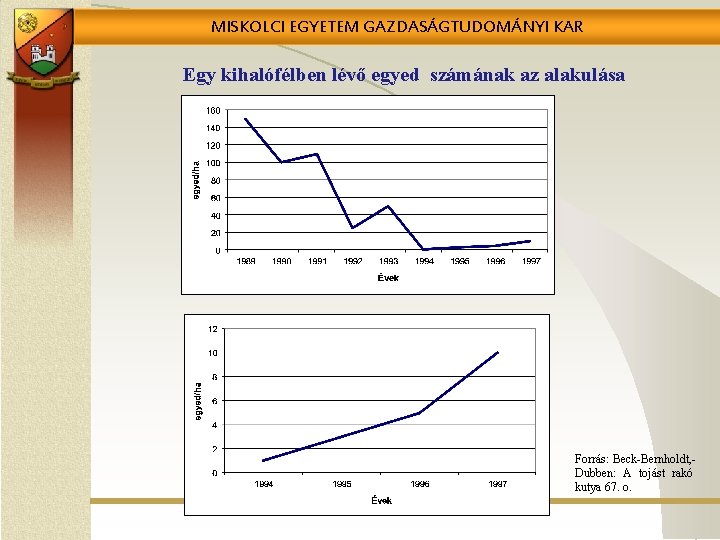
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Egy kihalófélben lévő egyed számának az alakulása Forrás: Beck-Bernholdt, Dubben: A tojást rakó kutya 67. o.

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Idősorok egyszerű elemzési módszerei • Számtani átlag (tartamidősorok adataiból - flow változóknál) • Kronológikus átlag (állapot idősor adataiból – stock változóknál) 7

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Átlagos változás mutatói : • a változás átlagos mértéke: Az időegységre jutó átlagos változást adja meg. • a változás átlagos üteme: Ez viszonyszámként adja meg a változás ütemét, fejlődést tükröz 8

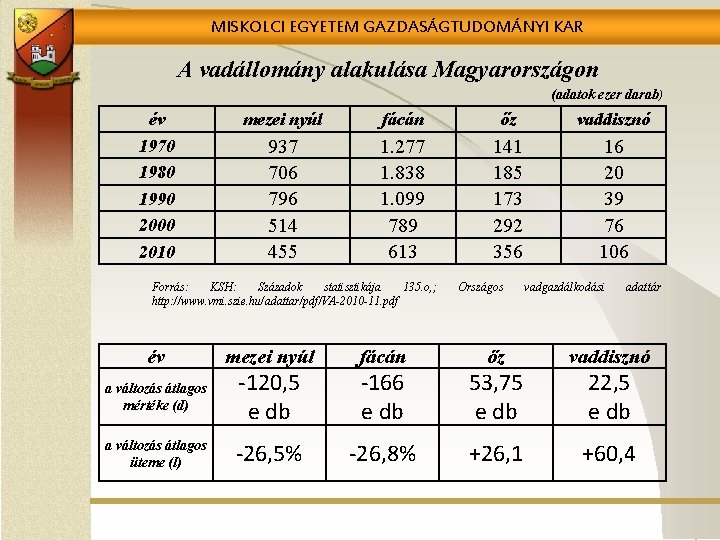
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR A vadállomány alakulása Magyarországon (adatok ezer darab) év 1970 1980 1990 2000 2010 mezei nyúl fácán őz vaddisznó 937 706 796 514 455 1. 277 1. 838 1. 099 789 613 141 185 173 292 356 16 20 39 76 106 Forrás: KSH: Századok statisztikája 135. o, ; http: //www. vmi. szie. hu/adattar/pdf/VA-2010 -11. pdf év mezei nyúl a változás átlagos mértéke (d) -120, 5 e db fácán a változás átlagos üteme (l) -26, 5% Országos vadgazdálkodási adattár -166 e db őz 53, 75 e db vaddisznó -26, 8% +26, 1 +60, 4 22, 5 e db

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Dinamikus viszonyszámok • lánc viszonyszám • bázisviszonyszám

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Az idősorok elemzésének bonyolultabb eszközei 11

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Az idősorelemzés megközelítési módjai q q Determinisztikus idősorelemzés: Az idősor értékeinek alakulását az idő múlásával magyarázza. Két egymástól azonos távolságra lévő időpillanat között ugyanolyan jellegű változást tételez fel, bárhol van ez a két időpont az időskálán. Sztochasztikus idősorelemzés: Az idősor adatai időben véletlenszerűen lejátszódó, sztochasztikus folyamatok empirikus adatai. 12

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Determinisztikus idősorelemzés feltételezi, hogy az idősor előre adott pályát követ. Legismertebb modellje a dekompozíciós modell, amely feltételezi az egyes elemek szétválaszthatóságát.

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Az idősorok összetevői alapirányzat vagy trend, q periodikus ingadozás, q ciklus, q véletlen ingadozás. q 14

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Alapirányzat vagy trend Jele: q q az idősorban tartósan érvényesülő tendencia a fejlődés legfontosabb komponense. több tényező együttes hatásának a következménye, alapvetően társadalmi-gazdasági törvényszerűségek határozzák meg. 15

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Periodikus ingadozás Jele: sj q Az idősorokban rendszeresen ismétlődő hullámzás. q Leggyakoribb típusai: az idényszerű ill. szezonális ingadozások q Az idényhatás állandó periódushosszúságú hullámzás, ritmikus ingadozás; q általában olyan idősorokban állapíthatjuk meg jelenlétét, amelynek adatai egy évnél rövidebb időszakra (hónap, negyedév) vonatkoznak. q Vannak olyan periodikus hullámzások is, amelyeknél a periódus rövidebb, mint egy év. 16

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Ciklus Jele: c q Olyan periodikus ingadozás az idősorban, amely kevésbé szabályos, jelenlétét csak hosszabb idősorok alapján lehet felfedni és tanulmányozni. q Az ingadozások periódusának hosszúságát egyrészt természeti okok is befolyásolhatják q Fő típusai az ún. gazdasági (konjunktúra) ciklusok. 17

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Véletlen ingadozás Jele: vij q Ezt az összetevőt valószínűségi változónak tekintjük. q Véletlennek igen sok, egyenként nem jelentős, egymás hatását elősegítő vagy keresztező végső eredményét tekintjük. q A véletlen hatás eredménye, hogy az idősorok adatai a trendből, illetve a periodikus komponensből adódó görbe körül sztochasztikusan ingadoznak. 18

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Idősorok elemzésének feladatai 1. A fejlődés alapirányzatának megismerése, miközben eltekintünk a többi összetevőitől. Az idősort mintegy ki akarjuk simítani: a szezonális, a ciklikus és a véletlen ingadozást "el akarjuk tüntetni", hogy a trendvonalat tisztán lássuk. 2. A mozgó átlagolás vagy a regressziós módszerekből származtatható analitikus kiegyenlítéssel számszerűsíteni az idősorban rejlő tendenciákat. 3. Az idényszerű hullámzás jellemzőinek mérése, amelynek során ki kell küszöbölni az idősorban érvényesülő trendhatást és a véletlen ingadozást (gazdasági ciklus hatását). 4. A konjunktúrahullám (gazdasági ciklus) kimutatása (a többi hatás kiszűrésével). 5. A véletlen hatások kezelése. 19

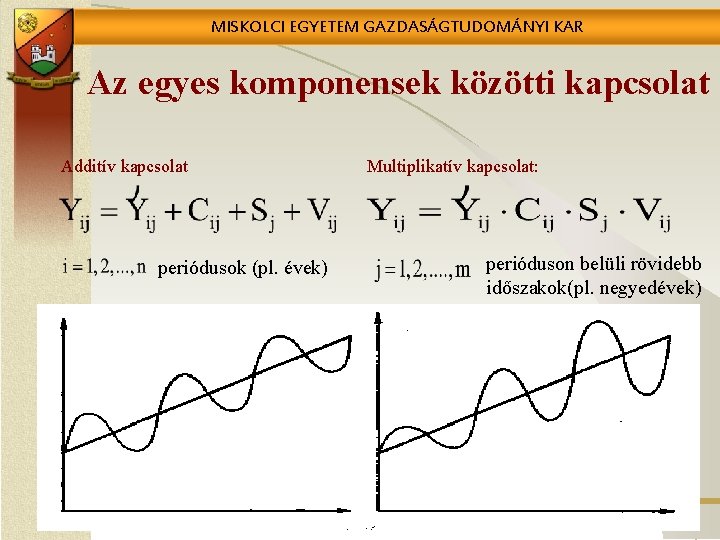
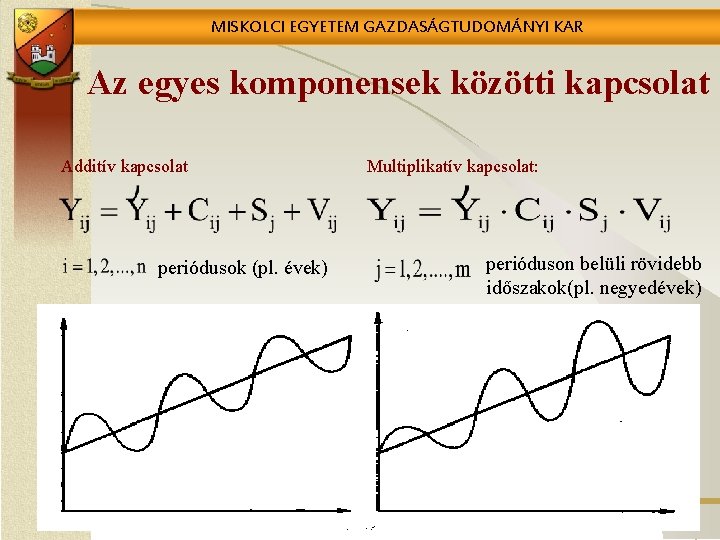
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Az egyes komponensek közötti kapcsolat Additív kapcsolat periódusok (pl. évek) Multiplikatív kapcsolat: perióduson belüli rövidebb időszakok(pl. negyedévek)

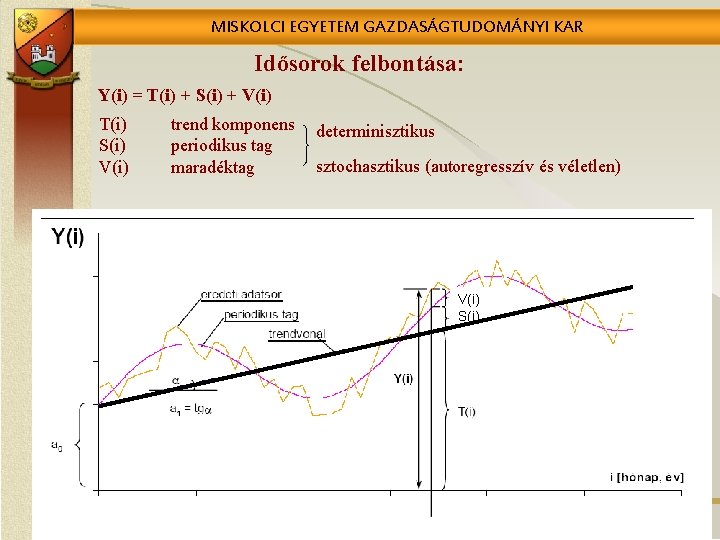
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Idősorok felbontása: Y(i) = T(i) + S(i) + V(i) T(i) S(i) V(i) trend komponens periodikus tag maradéktag determinisztikus sztochasztikus (autoregresszív és véletlen) V(i) S(i)

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Trendszámítás A trendszámítás feladata az idősor fő komponensének, az alapirányzatnak a kimutatása. Az idősor kiegyenlítése, kisimítása a célunk úgy, hogy a periodikus ingadozás és a véletlen ingadozás hatását kiküszöböljük. 22

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Trendszámítás Analitikus trendszámítás: az idősor alapirányzatát valamilyen matematikai függvénnyel írjuk le Mozgóátlagolás módszere: a t. időszakhoz tartozó trendértéket a környező időszakok adatainak dinamikus átlagaként határozzuk meg.

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Trendszámítás mozgó átlagolással A mozgó átlagolás alapgondolata az, hogy a trendet az eredeti sor dinamikus átlagaként állítjuk elő. A számítás menete a következő: q Kiszámítjuk az idősor első „k” adatának egyszerű számtani átlagát. Ez az első trendérték, amelyet az érintett időszak közepéhez - vagyis a (k+1) 1/2 -edik időszakhoz - rendelünk. Ezután elhagyjuk az első adatot, és ehelyett vesszük a következő (k+1)-ediket. q Ismét átlagot számítva nyerjük a következő mozgó átlagot, vagyis trendértéket, amelyet a megfelelő időszakhoz rendelünk. q Így haladunk, amíg az utolsó adatot is felhasználjuk. q Az eredményül kapott trendértékek sorozata a kiegyenlített idősor. 24

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Háromtagú mozgó átlagok számítása 25

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Háromtagú mozgó átlagok számítása Páratlan k tagszám esetén az yt (t = 1, 2, . . . , n) idősorból számított k tagú mozgó átlagok sorozata a t = j+1 -edik időszaktól a t = n-j-edik időszakig tart, ahol j = (k-1)/2. A t-edik időszakhoz rendelt mozgó átlag: 26

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Páros tagszámú mozgóátlag számítása q q Páros tagszám esetén az az időszak, amelyet a mozgó átlag jellemez, mindig két, eredetileg megadott időszak közé esik, így pl. 12 tagú átlagnál a 6. és 7. időszak közé. Ezen a helyzeten egy újabb művelet, az ún. középre igazítás, vagy centírozás beiktatásával segítünk. A középre igazítás úgy történik, hogy a kiszámított mozgó átlagokat páronként rendre átlagoljuk, vagyis újabb, ezúttal kéttagú mozgó átlagok sorozatát számítjuk ki. Ezek a trendértékek már a megadott időszakra vonatkoznak. 27

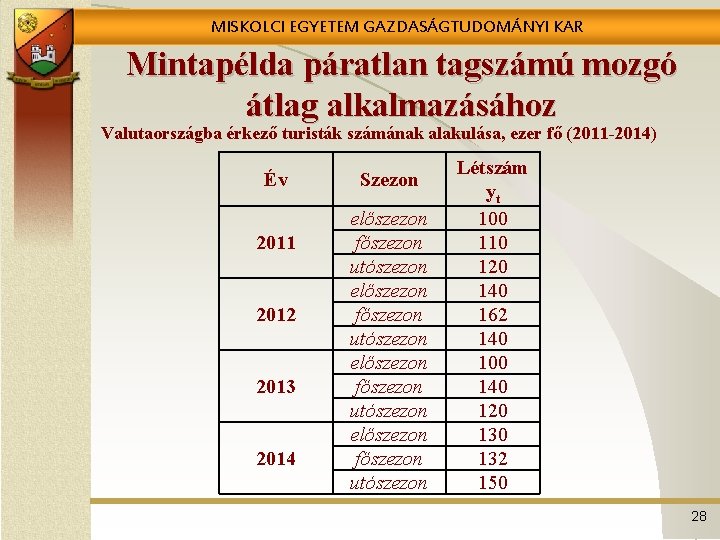
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintapélda páratlan tagszámú mozgó átlag alkalmazásához Valutaországba érkező turisták számának alakulása, ezer fő (2011 -2014) Év 2011 2012 2013 2014 Szezon előszezon főszezon utószezon Létszám yt 100 110 120 140 162 140 100 140 120 132 150 28

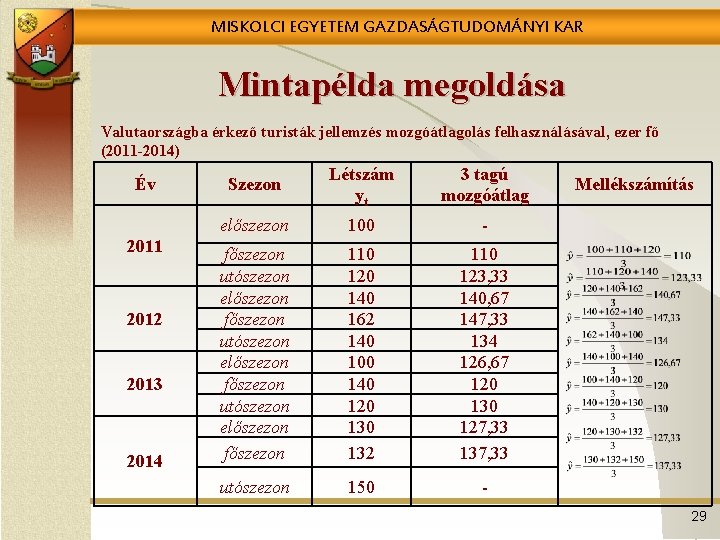
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintapélda megoldása Valutaországba érkező turisták jellemzés mozgóátlagolás felhasználásával, ezer fő (2011 -2014) Év 2011 2012 2013 2014 Szezon Létszám yt 3 tagú mozgóátlag előszezon 100 - főszezon utószezon előszezon főszezon 110 120 140 162 140 100 140 120 132 110 123, 33 140, 67 147, 33 134 126, 67 120 130 127, 33 137, 33 utószezon 150 - Mellékszámítás 29

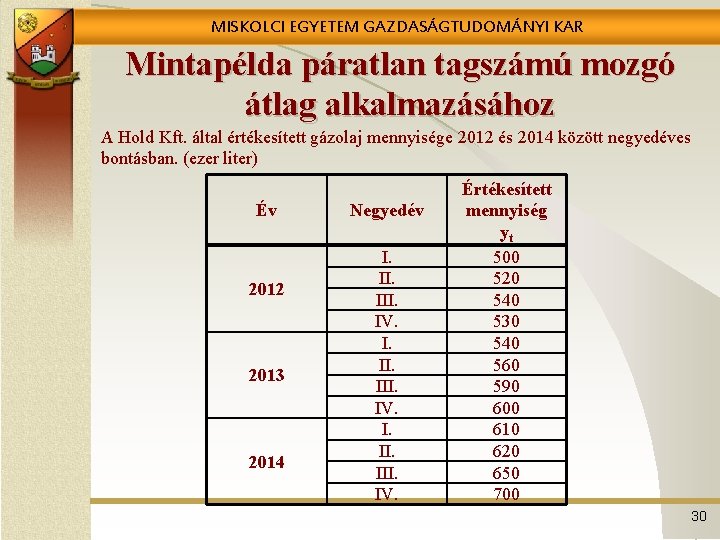
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintapélda páratlan tagszámú mozgó átlag alkalmazásához A Hold Kft. által értékesített gázolaj mennyisége 2012 és 2014 között negyedéves bontásban. (ezer liter) Év 2012 2013 2014 Negyedév I. II. III. IV. Értékesített mennyiség yt 500 520 540 530 540 560 590 600 610 620 650 700 30

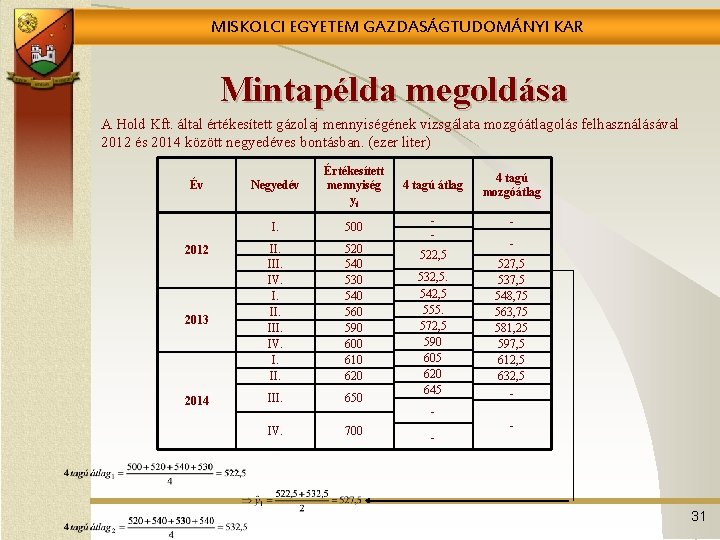
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintapélda megoldása A Hold Kft. által értékesített gázolaj mennyiségének vizsgálata mozgóátlagolás felhasználásával 2012 és 2014 között negyedéves bontásban. (ezer liter) Év 2012 2013 2014 Negyedév Értékesített mennyiség yt 4 tagú átlag 4 tagú mozgóátlag I. 500 - - II. III. IV. I. II. 520 540 530 540 560 590 600 610 620 III. 650 IV. 700 522, 5 532, 5. 542, 5 555. 572, 5 590 605 620 645 527, 5 537, 5 548, 75 563, 75 581, 25 597, 5 612, 5 632, 5 - - - 31

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mozgó átlagolás jellemzői q q q A kapott mozgóátlag, mint trend megmutatja az idősor alapirányzatát, miközben eltekintünk a többi komponenstől. A véletlen hatás kiküszöbölését (csökkentését) az átlagolás művelete révén érjük el. A véletlen kikapcsolása annál tökéletesebb, minél nagyobb tagszámú mozgó átlagokat számítunk. A periodikus ingadozás hatását a mozgó átlag tagszámának megfelelő kijelölésével küszöbölhetjük ki. Fontos, hogy mindegyik mozgó átlag átfogjon egy (vagy több) teljes idényciklust. A mozgó átlag tagszáma: egy-egy ciklushoz tartozó adatok számával legyenlő vagy annak egész számú többszöröse legyen. 32

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Analitikus trendszámítás q q q Analitikus trendszámítás: A vizsgált jelenség tartós irányzatát az idő függvényében valamilyen regressziós függvénnyel határozzuk meg. Az analitikus trendszámítás a leggyakrabban alkalmazott szűrő és simító eljárás. Az analitikus trendszámítás esetén két kérdést kell tisztázni: q q Milyen típusú függvénnyel akarjuk leírni az idősort? Hogyan mérjük az illeszkedést, és mikor tekintünk egy illeszkedést jónak? 33

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Lineáris trend Alkalmazása: Ha azt tapasztaljuk, hogy az időegységenként bekövetkezett változás, abszolút értelemben közel állandó, a változás egyenletes. Lineáris trendfüggvény: 34

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR A paraméterek meghatározása 35

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR A paraméterek értelmezése b 0 paraméter: Az alapirányzat értéke a t=0 -val jelölt időpontban. Ha t=1, 2, …, n, akkor a vizsgálatba bevont időpontot megelőző időpont trend szerinti értéke. b 1 paraméter: Az időegységenkénti átlagos abszolút változás mértéke. Előjelétől függően növekedést vagy csökkenést jelez a vizsgálatba bevont időtartam alatt. 36

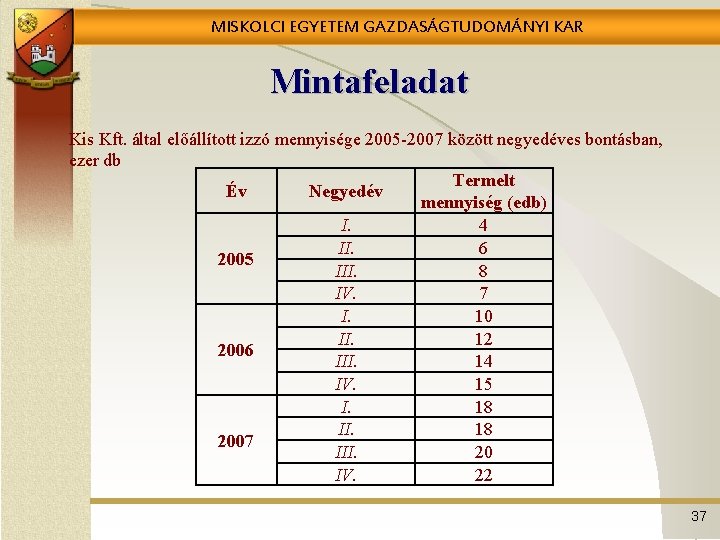
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintafeladat Kis Kft. által előállított izzó mennyisége 2005 -2007 között negyedéves bontásban, ezer db Termelt Év Negyedév mennyiség (edb) I. 4 II. 6 2005 III. 8 IV. 7 I. 10 II. 12 2006 III. 14 IV. 15 I. 18 II. 18 2007 III. 20 IV. 22 37

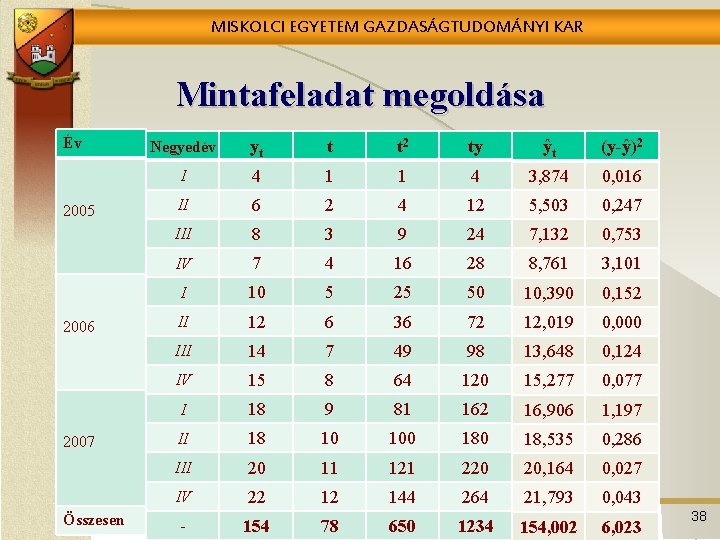
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintafeladat megoldása Év 2005 2006 2007 Összesen Negyedév yt t t 2 ty ŷt (y-ŷ)2 I 4 1 1 4 3, 874 0, 016 II 6 2 4 12 5, 503 0, 247 III 8 3 9 24 7, 132 0, 753 IV 7 4 16 28 8, 761 3, 101 I 10 5 25 50 10, 390 0, 152 II 12 6 36 72 12, 019 0, 000 III 14 7 49 98 13, 648 0, 124 IV 15 8 64 120 15, 277 0, 077 I 18 9 81 162 16, 906 1, 197 II 18 10 100 18, 535 0, 286 III 20 11 121 220 20, 164 0, 027 IV 22 12 144 264 21, 793 0, 043 - 154 78 650 1234 154, 002 6, 023 38

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintafeladat megoldása Év Negyedév yt t t 2 ty ŷt (y-ŷ)2 Összesen - 154 78 650 1234 154, 002 6, 023 Normálegyenletek a t=1, 2, …, n számítással: 154=12 b 0+78 b 1 1234=78 b 0+650 b 1 Az egyenletrendszer megoldásával kapott paraméterek: b 0=2, 245 b 1=1, 629 Trendegyenlet: ŷ=2, 245+1, 629*t 39

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Relatív reziduális szórás q Megmutatja, hogy a becsült értékek a valós értékektől átlagosan hány %-kal térnek el. A mutató által eldönthető, hogy a vizsgált idősor milyen trendfüggvénnyel írható le a legjobban. q Jele: Ve q 40

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Relatív reziduális szórás kiszámítása a mintapélda alapján Reziduális szórásnégyzet meghatározása Az a függvény illeszkedik jobban, ahol ez a szórásnégyzet kisebb. Relatív szórás mutatószáma: Tehát a Kis Kft. által előállított izzó mennyiségének lineáris trenddel becsült értékei a valós értékektől átlagosan 5, 5%-kal térnek el. 41

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Exponenciális trend q Alkalmazása: Ha a vizsgált jelenség egyik időszakról a másik időszakra megközelítőleg mindig ugyanannyiszorosára, azonos százalékkal változik, azaz az időegységenkénti relatív változás ingadozik egy állandó körül. Az exponenciális trendfüggvény általános alakja: 42

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Exponenciális trend Az exponenciális függvény logaritmikus transzformációval lineáris alakra hozható. A paraméterek meghatározása visszavezethető a lineáris függvényre. A t=1, 2, …, n időpontban mért y 1, …, yn adatokból a legkisebb négyzetek módszerével meghatározhatjuk (új jelölések bevezetésével) az exponenciális trendfüggvényt. 43

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Exponenciális trend normálegyenletei 44

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Paraméterek értelmezése q q b 0 : a jelenség exponenciális trend szerinti értéke a t=0 -val jelölt időpontban b 1 : az időegységenkénti átlagos relatív változás jelzi, hogy a vizsgált időszak alatt a jelenség értéke időegységenként átlagosan hányszorosára változott 45

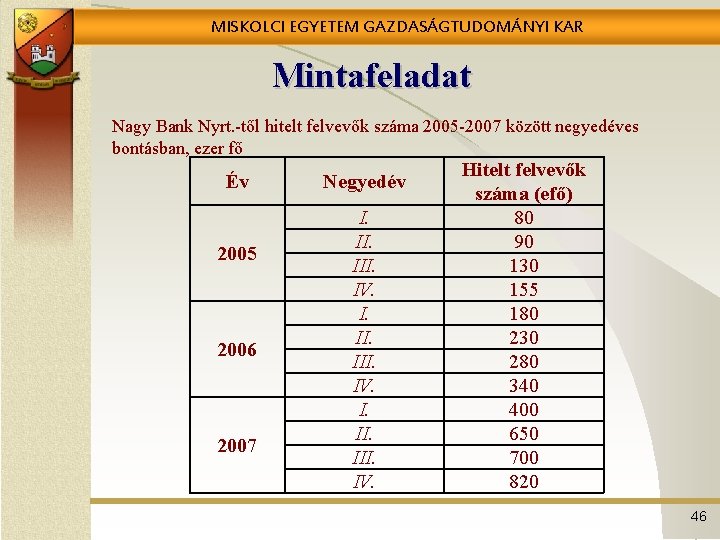
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Mintafeladat Nagy Bank Nyrt. -től hitelt felvevők száma 2005 -2007 között negyedéves bontásban, ezer fő Év 2005 2006 2007 Negyedév I. II. III. IV. Hitelt felvevők száma (efő) 80 90 130 155 180 230 280 340 400 650 700 820 46

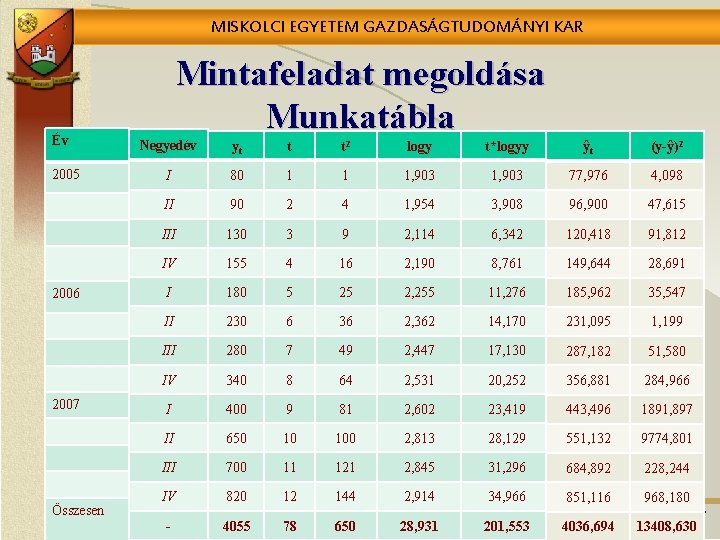
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Év 2005 2006 2007 Összesen Mintafeladat megoldása Munkatábla Negyedév yt t t 2 logy t*logyy ŷt (y-ŷ)2 I 80 1 1 1, 903 77, 976 4, 098 II 90 2 4 1, 954 3, 908 96, 900 47, 615 III 130 3 9 2, 114 6, 342 120, 418 91, 812 IV 155 4 16 2, 190 8, 761 149, 644 28, 691 I 180 5 25 2, 255 11, 276 185, 962 35, 547 II 230 6 36 2, 362 14, 170 231, 095 1, 199 III 280 7 49 2, 447 17, 130 287, 182 51, 580 IV 340 8 64 2, 531 20, 252 356, 881 284, 966 I 400 9 81 2, 602 23, 419 443, 496 1891, 897 II 650 10 100 2, 813 28, 129 551, 132 9774, 801 III 700 11 121 2, 845 31, 296 684, 892 228, 244 IV 820 12 144 2, 914 34, 966 851, 116 968, 180 - 4055 78 650 28, 931 201, 553 4036, 694 47 13408, 630

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Eredmények értelmezése Normálegyenletek a t=1, 2, …, n számítással: 28, 931=12 b 0+78 b 1 201, 553=78 b 0+650 b 1 Az egyenletrendszer megoldásával kapott paraméterek: Trendegyenlet: ŷ=62, 747*1, 2427 t „a” : 2004. IV. negyedévében az exponenciális trend szerinti létszám 62, 747 ezer fő volt. „b” : 1, 2427 a Nagy Bank-nál hitelt felvevők létszáma 2005 -2007 között negyedévenként átlagosan 1, 2427 -szeresére, azaz 24, 27%-kal növekedett. 48

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Az idősorok összetevői alapirányzat vagy trend, q periodikus ingadozás, szezonalitás q ciklus, q véletlen ingadozás. q 49

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Szezonalitás vizsgálata Jele: sj q q Az idősorokban rendszeresen ismétlődő hullámzás. Leggyakoribb típusai: az idényszerű ill. szezonális ingadozások Az idényhatás állandó periódushosszúságú hullámzás, ritmikus ingadozás Olyan idősorokban állapíthatjuk meg jelenlétét, amelynek adatai egy évnél rövidebb időszakra (hónap, negyedév) vonatkoznak. 50

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Az egyes komponensek közötti kapcsolat Additív kapcsolat periódusok (pl. évek) Multiplikatív kapcsolat: perióduson belüli rövidebb időszakok(pl. negyedévek)

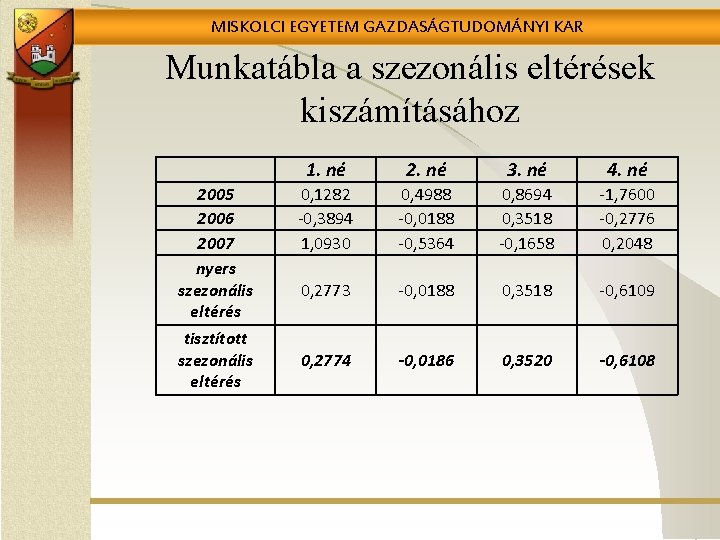
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Munkatábla a szezonális eltérések kiszámításához 2005 2006 2007 nyers szezonális eltérés tisztított szezonális eltérés 1. né 2. né 3. né 4. né 0, 1282 -0, 3894 1, 0930 0, 4988 -0, 0188 -0, 5364 0, 8694 0, 3518 -0, 1658 -1, 7600 -0, 2776 0, 2048 0, 2773 -0, 0188 0, 3518 -0, 6109 0, 2774 -0, 0186 0, 3520 -0, 6108

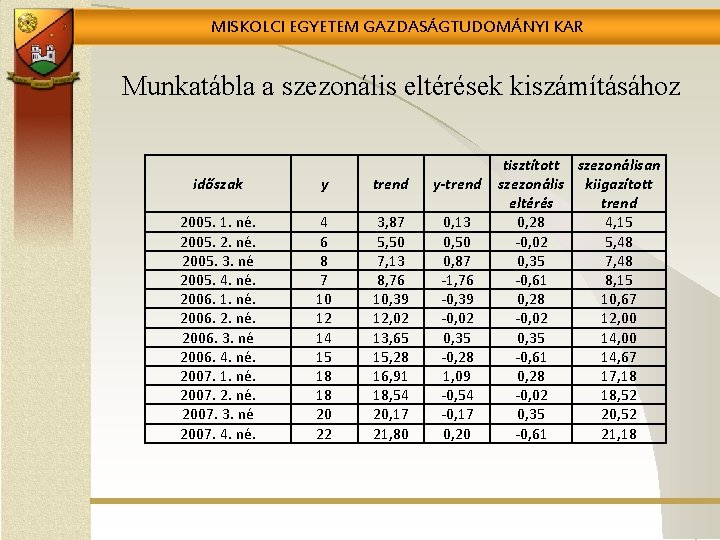
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Munkatábla a szezonális eltérések kiszámításához időszak y trend y-trend 2005. 1. né. 2005. 2. né. 2005. 3. né 2005. 4. né. 2006. 1. né. 2006. 2. né. 2006. 3. né 2006. 4. né. 2007. 1. né. 2007. 2. né. 2007. 3. né 2007. 4. né. 4 6 8 7 10 12 14 15 18 18 20 22 3, 87 5, 50 7, 13 8, 76 10, 39 12, 02 13, 65 15, 28 16, 91 18, 54 20, 17 21, 80 0, 13 0, 50 0, 87 -1, 76 -0, 39 -0, 02 0, 35 -0, 28 1, 09 -0, 54 -0, 17 0, 20 tisztított szezonálisan szezonális kiigazított eltérés trend 0, 28 4, 15 -0, 02 5, 48 0, 35 7, 48 -0, 61 8, 15 0, 28 10, 67 -0, 02 12, 00 0, 35 14, 00 -0, 61 14, 67 0, 28 17, 18 -0, 02 18, 52 0, 35 20, 52 -0, 61 21, 18

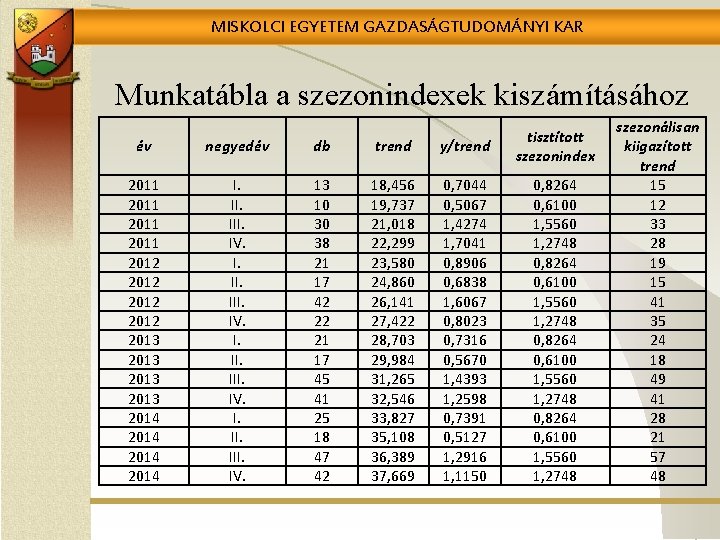
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Munkatábla a szezonindexek kiszámításához év negyedév db trend y/trend tisztított szezonindex 2011 2012 2013 2014 I. II. III. IV. 13 10 30 38 21 17 42 22 21 17 45 41 25 18 47 42 18, 456 19, 737 21, 018 22, 299 23, 580 24, 860 26, 141 27, 422 28, 703 29, 984 31, 265 32, 546 33, 827 35, 108 36, 389 37, 669 0, 7044 0, 5067 1, 4274 1, 7041 0, 8906 0, 6838 1, 6067 0, 8023 0, 7316 0, 5670 1, 4393 1, 2598 0, 7391 0, 5127 1, 2916 1, 1150 0, 8264 0, 6100 1, 5560 1, 2748 szezonálisan kiigazított trend 15 12 33 28 19 15 41 35 24 18 49 41 28 21 57 48

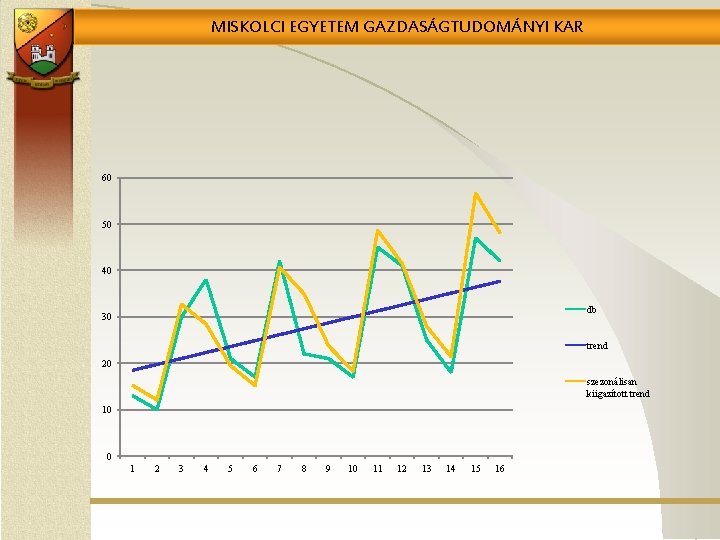
MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR 60 50 40 db 30 trend 20 szezonálisan kiigazított trend 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

MISKOLCI EGYETEM GAZDASÁGTUDOMÁNYI KAR Köszönöm a figyelmet! 56