Misc Topics in Testing Mc Cabes Cyclomatic Complexity

Misc Topics in Testing

Mc. Cabe’s Cyclomatic Complexity Number of “linearly independent paths” – useful in defining test coverage (See later) – Counts the number of closed loops in the graph • FA() = 0 • Fs(m 1, m 2) = m 1 + m 2 • FC(m 1, m 2) = m 1 + m 2 + 1 • Fl(m 1) = m 1 + 1 v(P) = #edges - #nodes +2 (Familiar? )

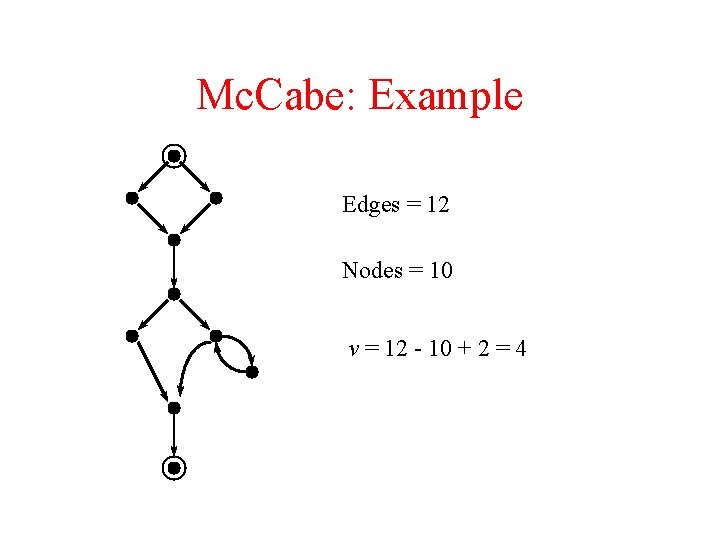
Mc. Cabe: Example Edges = 12 Nodes = 10 v = 12 - 10 + 2 = 4

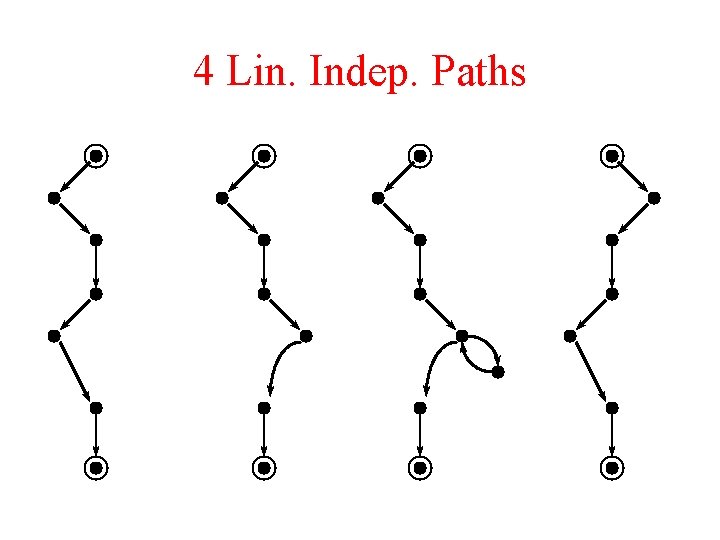
4 Lin. Indep. Paths

More generally. . . • Can define a set of prime flowgraphs – those which cannot be broken down by nesting – corresponding to the statements of the langauge • And a measure for each • Yields a Prime Decomposition Theorem: – “The decomposition of a flowgraph into primes is unique”

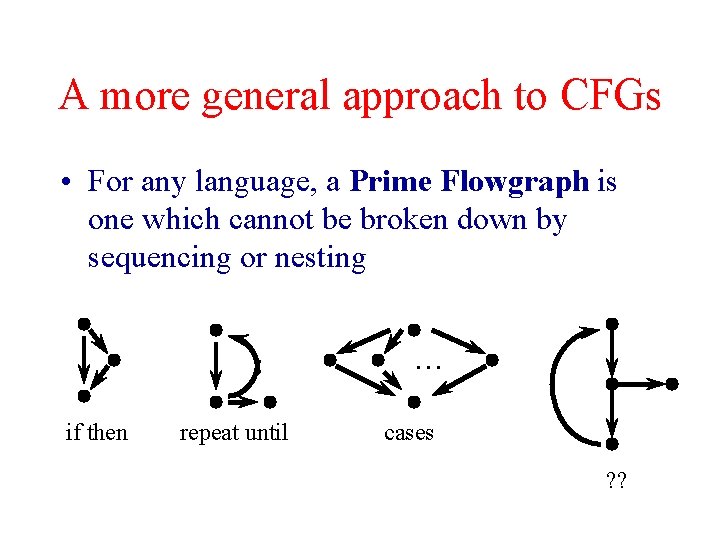
A more general approach to CFGs • For any language, a Prime Flowgraph is one which cannot be broken down by sequencing or nesting . . . if then repeat until cases ? ?

Hierarchical measures (again) • Define measure for each prime flowgraph • Define measure for sequencing • Define measure for nesting Eg. number of nodes: nd(P) = #nodes in P, for each prime

Example: Structuredness • Whether a program is structured can be seen as a measure as follows: str(P) = 1 if P is one of the allowed primes 0 otherwise str(F 1; . . . Fn) = min(str(F 1), . . . , str(Fn) str(F(F 1, . . . , Fn)) = min(str(F), str(F 1), . . . , str(Fn))

Linearly Independent Paths • The vector representation of a path is a vector which counts the number of occurrences of each edge. • A set of paths is l. i. if none can be represented as a linear combination of the others (in the vector representation).

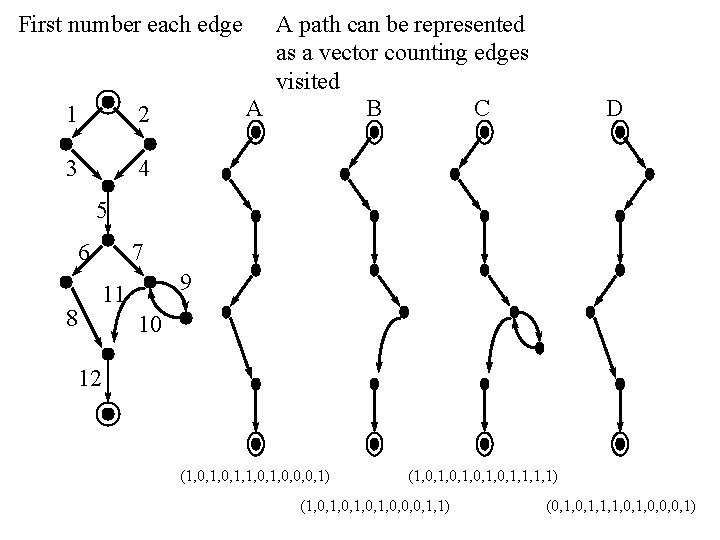
First number each edge 1 2 3 4 A path can be represented as a vector counting edges visited A B C D 5 6 7 9 8 11 10 12 (1, 0, 1, 1, 0, 0, 0, 1) (1, 0, 1, 1, 1, 1) (1, 0, 0, 0, 1, 1) (0, 1, 1, 1, 0, 0, 0, 1)

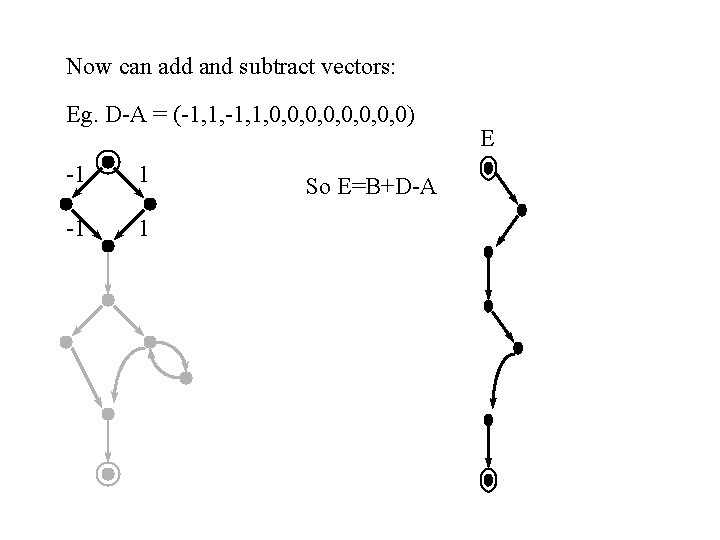
Now can add and subtract vectors: Eg. D-A = (-1, 1, 0, 0, 0) -1 1 So E=B+D-A E

How do we find test sets? • Given a test strategy it is not easy to find test cases that exercise the required paths – Even for Statement Coverage some parts of the code may be unreachable – A single path can achieve Branch Coverage for: while(. . . ) do “some complex program” but unlikely to be possible in practice

Domain Partitioning What have we been doing? • Partitioning input space according to some property • Selecting Test case inputs which are representatives of each partition – Eg to ensure different paths executed • Assuming behaviour similar for all values of partition

Boundary Value Analysis • Also important to test software at the boundaries of the partitions. – Less than (or equal)? – length of list (or n-1)? – closure reversal (“not <” is not “>”)? • How do we identify boundaries?

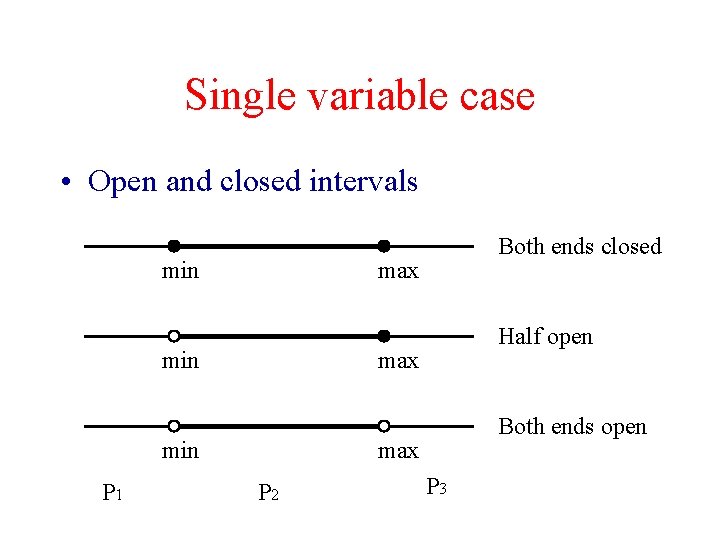
Single variable case • Open and closed intervals min max min Half open max min P 1 Both ends closed Both ends open max P 2 P 3

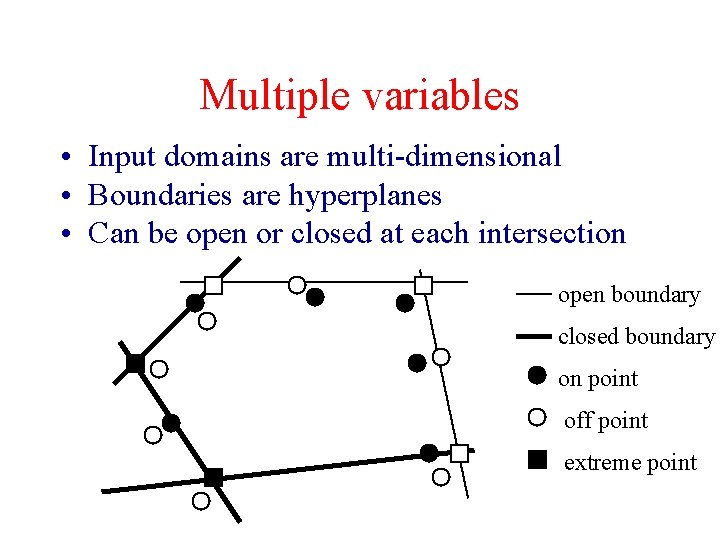
Multiple variables • Input domains are multi-dimensional • Boundaries are hyperplanes • Can be open or closed at each intersection open boundary closed boundary on point off point extreme point

Finding Test Cases • CFGs model software • Test strategy to select paths to test • Data flow Analysis to choose “best” test paths • Now need to find test inputs which exercise those paths

Example • Find All DU paths for example program • Find test cases which execute the paths

Program smallest(int p) (*p>2*) { int q = 2; while(p mod q > 0 AND q < sqrt p) do q : = q+1 ; if (p mod q = 0) then print(q, ’is factor’) else print(p, ’is prime’) ; } Usage CFG p 1 d 2 3 d u 4 5 8 u ud u 6 7 q u u u ADUP p 12343 1235 123435 12357 1234357 q 23 234 2356 43 434 4356

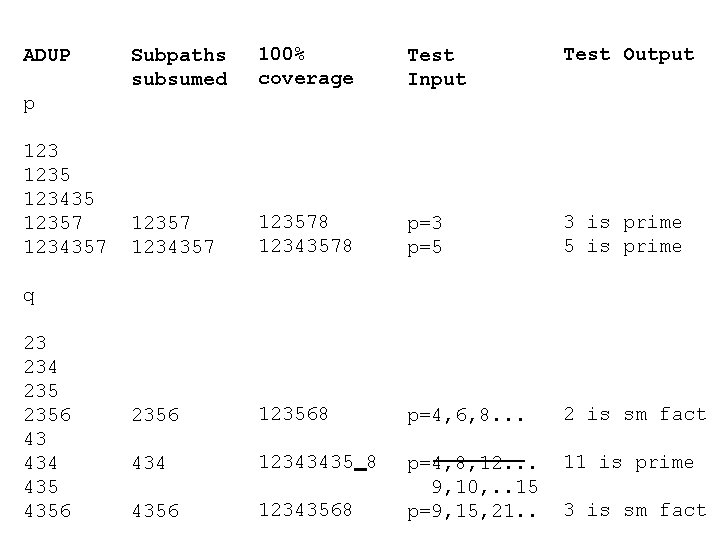
ADUP Subpaths subsumed 100% coverage Test Input Test Output 12357 1234357 123578 12343578 p=3 p=5 3 is prime 5 is prime 2356 123568 p=4, 6, 8. . . 2 is sm fact 434 12343435 8 11 is prime 4356 12343568 p=4, 8, 12. . . 9, 10, . . 15 p=9, 15, 21. . p 1235 123435 12357 1234357 q 23 234 2356 43 434 4356 3 is sm fact

How were test cases found? • Required outcome at each predicate node • Consider all requirements together • Guess a value that will satisfy them • Can we improve on this!

Symbolic Execution • How to find test inputs to exercise a path? – Need certain choice at each predicate node – Give a symbolic value to each variable – Walk the path collecting requirements on symbolic input • Then have a set of inequalities to solve • Example: Find test cases for each path by symbolic execution:

Path 123578 p q smallest(p) { int q = 2; while(p mod q > 0 AND q < sqrt p) do q : = q+1 ; if (p mod q = 0) then print(q, ’is factor’) else print(p, ’is prime’) ; } Conditions Candidates X=4, 6, 8, . . . 3, 4 X=3, 5, 7, . . . X Y X 2 F X 2 X mod 2 =0 OR 2 ge sqrt X F X 2 X mod 2 > 0 X 2 Solutions X=3

Path 12343578 Conditions Candidates X mod 2 > 0 2 < sqrt X X=3, 5, 7, . . . X=5, 6, 7. . while (F) X mod 3 = 0 OR 3 ge sqrt(X) X=3, 6, 9. . 3, 4. . 9 if (F) X mod 3 > 0 X=4, 5, 7, 8, . . p q X Y X 2 while (T) X Solutions 3 X is prime X=5, 7 Output: 5 is prime 7 is prime

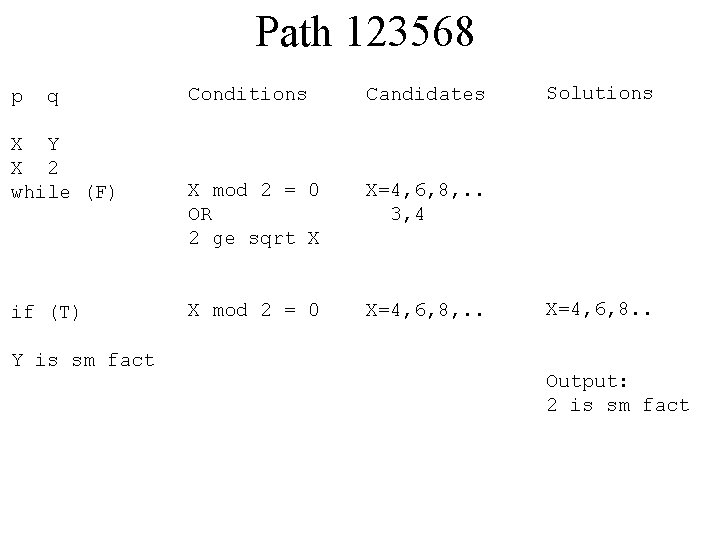
Path 123568 p q X Y X 2 while (F) if (T) Y is sm fact Conditions Candidates X mod 2 = 0 OR 2 ge sqrt X X=4, 6, 8, . . 3, 4 X mod 2 = 0 X=4, 6, 8, . . Solutions X=4, 6, 8. . Output: 2 is sm fact

Path 12343568 Conditions Candidates X mod 2 > 0 2 < sqrt X X=3, 5, 7. . X=5, 6, 7. . while (F) X mod 3 = 0 OR 3 ge sqrt(X) X=3, 6, 9. . 3, 4. . 9 if (T) X mod 3 = 0 X=3, 6, 9. . p q X Y X 2 while (T) X Solutions 3 Y is sm fact X=9, 15, 21. .

Path 12343435_8 p q X 2 while (T) X 3 while (T) X 4 while (F) Conditions Candidates Solutions X mod 2 > 0 2 < sqrt X X=3, 5, 7. . X=5, 6, 7. . [5, 7, 9, 11, 13. . X mod 3 > 0 3 < sqrt X X=4, 5, 7, 8. . [5, 7, 11, 13, 17 X=10, 11, 12. . [11, 13, 17, 19. . X mod 4 = 0 OR 4 ge sqrt(X) X=4, 8, 12. . 3, 4. . 16 [none from this [11, 13 X=. . . [must be false X=11, 13 if (_) X mod 4 ? 0 ? ? ? ? Output: 11 is prime 13 is prime

Difficulties with Symbolic Execution • Generally, many paths are not feasible • Conditions can become complex: – when complex expressions on rhs of assignments – then program variables are complex expressions in terms of the symbolic vars • Sets of conditions can be computationally complex to solve

Possible Solutions • Computational Complexity: – Use numerical methods to calculate the tests • Straight line equivalents • Program Instrumentation – Adaptive testing (later) • Complex predicates – Condition/Decision strategies (later) • Many Infeasible paths – Adaptive testing (later)

Straight Line equivalents • Construct the “straight line” program corresponding to the path required. • replace predicates with path constraints – a real valued expression which records the requirement as a minimisation • Solve the path constraints using numerical methods

Path Constraints • Eg. if(x = y) is replaced by c 1 : = abs(x-y) • and if(x>y) is replaced by c 2 : = x-y • Then we must minimise the ci • Can use numerical methods to do this

Program instrumentation • generally - a method to allow testing of a unit in place by augmenting program • Here - add function calls which record value of key variables • replace predicates with calls which guarantee correct path is taken • run program to generate conditions • Again use numerical methods to solve

Conditions and Decisions • Above strategies do not take account of predicates with more than one conjunct • There are more strategies which distinguish – Conditions - the individual clauses of predicate, from – Decisions - the outcome of evaluating the whole predicate

Condition Coverage • Achieve all possible combinations of simple Boolean conditions at each decision node • In critical real-time applications over half of statements may be Boolean expressions • Several variants of strategies which account for individual conditions

Example Condition Strategies • Decision coverage (DC) – every decision tested in each possible outcome • Condition/Decision coverage (C/DC) – as above plus, every condition in each decision tested in each possible outcome • Modified Condition/Decision (MC/DC) – as above plus, every condition shown to independently affect a decision outcome (by varying that condition only) • Multiple-condition coverage (M-CC) – all possible combinations of conditions within each decision taken

Modified Condition/Decision Coverage • Multiple-condition coverage is strongest but grows exponentially in # conditions • Modified C/D is linear like C/D • Eg. For A and B – (T, T) required to exercise decision true – (F, T) required for independence of A – (T, F) required for independence of B – (F, F) not required • MC/DC (among others) is required for flight -critical commercial avionics software

Further Problems with Symb. Ex. • When loop conditions are input dependent • When array indices are input dependent • When external functions are called

Adaptive Testing The above approach has been in 4 stages: 1) Construct the control flow graph – a parsing problem - automatable – can all add “instrumentation” here 2) Choose the test paths – According to some test strategy – CFG - possibly with data flow considerations

Four stages (cont. ) 3) Choose the test cases – by symbolic execution and simultaneous ineqs • or by backwards substitution – can reveal Infeasible paths requiring reverting to stage 2. 4) Execute the test cases – Only now do we execute the program • Adaptive testing merges stages 2), 3) and 4)

Problems with 4 -stage approach • Infeasible paths (stage 3) require selection of new paths (return to stage 2) • Computational complexity of test case selection Adaptive testing develops test cases one at a time and uses result of previous test case execution to help select next test case

Inductive Strategies • Choose first test input x 1 (perhaps at random) • Execute test and record path taken, p 1 • Say k-1 tests have been done giving {(x 1, p 1), . . . (xk-1, pk-1)} • use some strategy to select xn Several such strategies exist.

Diagonalisation Important “method” in Mathematics: • Cantor’s uncountability of Reals • Godel’s Incompleteness • Undecidability of Halting problem For list of lists, find a new list by choosing an element different from each on the diagonal A 11, A 12, A 13, . . . A 21, A 22, A 23, . . . A 31, A 32, A 33, . . . New = B 1, B 2, B 3, . . . where B 1 = A 11 B 2 = A 22 B 3 = A 33. . .

Diagonalisation (2) • Each path pi gives a conjunctive predicate Pi • These predicates characterise a set of nonoverlapping subdomains of the input space • We must find a new input xk not in any Pi • Let Pi be conjunction of Ci, 1, Ci, 2, . . . Ci, ki • For each i, choose xk to violate some Ci, j – eg. xk not in Ci, i

Path Prefix Strategy [Prather and Myers, IEEE Trans. SE-13(7) 1987] For Branch coverage • For a path p, define its reversible prefix q – the initial portion of p to the first decision node where the branches are not yet fully covered • A reversal of p is then any path with same reversible prefix but then a different continuation

Path Prefix Strategy (2) • Choose first input in some way and execute to give first path, p 1 • Given p 1, . . . , pk-1, let pi be path with shortest reversible prefix • Choose next input to give a reversal of pi • Execute and add the new path to set of paths

Path Prefix: earlier example • Choose first input p = 3 (say) – execution gives path p 1 = 12357 – Reversible prefix = 123, Reversal = 1234. . • Deduce second input, p = 5 – execution gives path p 2 = 12343578 – reversible prefix 123435 – path p 1 also now has reversible prefix 1235 – choose shorter p 2, Reversal = 12356 • Deduce 3 rd input, p = 4 – execution gives path p 3 = 123568 • All branches covered

Problems with Path prefix • Still need to deduce input for new path – the inversion problem (later) • Still may get infeasible paths – absolute infeasibility - a path can never be executed – relative infeasibilty - a path cannot be the continuation of any of the current reversible prefixes

Example of relative infeasibilty Conditionals in sequence: 1 2 3 simple(bool x, y) if(x = true) then S 1 else S 2; if(x xor y = true) then S 3 else S 4; if(x and y = true) then S 5 else S 6; in 1 = (false, false) p 1 = F, F, F reverse at 1 gives: in 2 = (true, false) p 2 = T, T, F reverse p 1 at 2 gives F, F, T - infeasible reverse p 2 at 2 gives T, T, T infeasible but T, F, T is feasible, eg in 3 = (true, true) - # paths to node grows exponentially - # previous nodes grows linearly

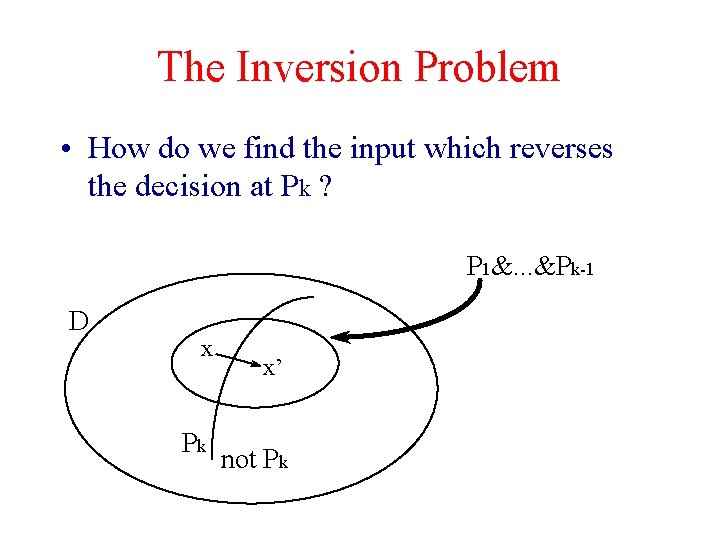
The Inversion Problem • How do we find the input which reverses the decision at Pk ? P 1&. . . &Pk-1 D x Pk x’ not Pk

The Inversion Problem (2) • • • Need to find x’ given x Done by Back Substitution execute with x recording all states for prefix pick change of a variable to change Pk substitute back through program logic to calculate required input – same as for 4 step approach but with actual values – For real-valued conditions can use grad(Pk) to cross boundary via normal

Advantages of adaptive approach • Informal common sense tells us: – Change only one thing at a time – Exploit nearness of previous test cases to the required path • Formal analysis gives us: – overall complexity of adaptive approach is less than 4 stage approach [Myers, SEJ 7(1) 1992]

References • ADTEST, Gallagher and Narasimhan, IEEE Trans. SE-23(8), 1997. • Symbolic Execution, Girgis, SEJ 7(4), 1992. • Instrumentation, Luo, Probert and Ural, Software Engineering Journal (SEJ) 10(6), 1995. • Path Prefix, Prather and Myers, IEEE Trans. SE 13(7), 1987. • Complexity of adaptive, Myers, SEJ 7(1), 1992. • MC/DC, Chilenski and Miller, SEJ 9(5) 1994.