MIS 131 Introduction to Algorithms and Programming 20152016

MIS 131 Introduction to Algorithms and Programming 2015/2016 Fall - Chapter 2 – Algorithms, Pseudocodes and Flowcharts © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved. 1

2 Objectives • In this chapter, you will learn: – To understand basic problem solving techniques. – To be able to develop algorithms through the process of top-down, stepwise refinement. – To be able to convert the algorithm to pseudocode and flowcharts – To be able to write simple Java Programs © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

3 2. 1 Introduction • Before writing a program: – Have a thorough understanding of the problem – Carefully plan an approach for solving it – The program should be carifully designed • While writing a program: – Know what “building blocks” are available – Use good programming principles © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

4 2. 2 Algorithms • Computing problems – All can be solved by executing a series of actions in a specific order • Algorithm: procedure in terms of – Actions to be executed – The order in which these actions are to be executed • Program control – Specify order in which statements are to be executed © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Example 2. 1 Registration • A real life example • Describe steps of registration to an universty • step by step description of how a new commer is to register to an universty © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Example 2. 1. Registering to an University Algorithm • 1 Obtain required forms • 2 Fill out the forms • 3 Other required materials are prepaired – identification, diploms • 4 Registration fee is paid • 5 forms are submited to the relevent person • 6 if something is mising – goto step 2 • 7 Sign the agrement • 8 Registration is complete © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved. 6

7 Notice that • When each step is compleated – next step is passed • it is also possible to branch a previous or later step – in this example from step 6 to srep 2 • The action in each step may depend on a condition – in step 6 if everything is OK continue otherwise branch to step 2 • Each of these steps may consists of sub steps – ex: step 2 fill out forms: there may be three different forms – each of which may be a sub step of step 2 • 2 a : a from for registration office • 2 b : a form for university hospital • 2 c : a form for university library © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

8 Example 2. 2 Calculating area of a regtangle • • Calcuating area of a rectangle Algortihm: 1 - Start 2 - Get value of hight 3 - Get value of width 4 - Multiply hight by width to obtain area 5 - Display the resultingf area to the screen 6 - Stop © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

9 Note • • Without performing steps 2 and 3 Step 4 can not be performed Similarly Without performing steps 4 Step 5 can not be performed But Steps 2 and 3 can be interchanged © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

10 Exercis 2. 1 • Pick up a real life situation that interest you • for example: – driveing a car – cooking egg or cake • Construct the algorithm to someone who does not have any idea obout that situation © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

11 2. 3 Pseudocode • Pseudocode – Artificial, informal language that helps us develop algorithms – Similar to everyday English – Not actually executed on computers – Helps us “think out” a program before writing it • Easy to convert into a corresponding C program • Consists only of executable statements © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

12 Pseudocode for Example 2. 2 1 Start 2 a Display “enter height of the rectange” 2 b Input heigth 3 a Display “enter width of the rectange” 3 b Input width 4 Set area = height * width 5 Display “the area of the regtanle” , area 6 Stop or end © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

13 Note That • In the algorithm : – Getting the height from the user • In the pseudocode – – first write a message to be displayed in the screen informing the user what to enter as an input Then let the user enter a real number and press ENTER key The number entered by the user is stored in the variable heigth • Similarly for getting width of the rectangle © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

14 • When the pseudocode is implemented in any programming languare such as Java, C# or Python • The user first see the message “Enter heitht of the rectanvge ” in the computers screen The user is expected to enter real number for the height end press ENTER key • The Input heigth statement – obtains the chacters entered by the user converts into a numerical variable called height to be used in subsequent steps of the pseudocode or program © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

15 Building Blocks • • • Input output transfer Calculations in between - processing Decision making Iteration Variables – Store data in memory – different types in different languages – İntegers, real, character, string. . . • Input: obtain a value from the user and store in a variable – enter a value for radius of a circle to compute its area – enter your name lastname id number – make a choice Yes/No to save or not © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

16 Variables – Store data in memory – different types in different languages – İntegers, real, character, string. . . • numerical variables – heigth, width, age total. Sales • Strings : – Name, last name, address, e-mail – “Bertan” , “Badur”, “badur@boun. edu. tr” – usually presented in quats “. . . ” © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

17 Variable in daily iife • what is your name? – stored in your memory as a string • what is your age or weight – you know the meaning of agfe or weight – stroded as an integer or real and changes over time • What is your GPA – you know wht GPA is but not yet has a value as a new studeent • What is your garbay score – – this does not make a sense to you no such think in your memory when asked you are supprised or hesitate to answer BUT A COMPUTER PRGRAM FAİLS © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

18 Outtput • Output: display the results of the problem – some variables • display area – constant messages • Display “welcome to Java” • Display “you failed to register” – expressions • Display pi*r 2 – or a mixture of them • Display “the area is: “, area – E. g. : displays when the value of area is 200 – the area is: 200 © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

19 Calculations - processing • • Calculations aritmetic and logical computations intermediate resulst are also in variables E. g. : – Set area = hight*width • area is the product of hight and width – E. g. : • Set value. Added. Tax = tax. Rate*base. Payment – E. g. : – Set total = total + new grade • add new grade to the total © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

20 2. 4 Control Structures • Sequential execution – Statements executed one after the other in the order written • Transfer of control – When the next statement executed is not the next one in sequence – Overuse of goto statements led to many problems • Bohm and Jacopini – All programs written in terms of 3 control structures • Sequence structures: Built into Java. Programs executed sequentially by default • Selection structures: Java has three types: if, if…else, and switch • Repetition structures: Java has three types: while, do…while and for © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

21 Simple Building Blocks • We will start with – input • get data from the user • store in variables – process or calculation • Store the results in variables – output • dsiplay message and/or variables to the screen • Variables of different types – Stored in memory © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

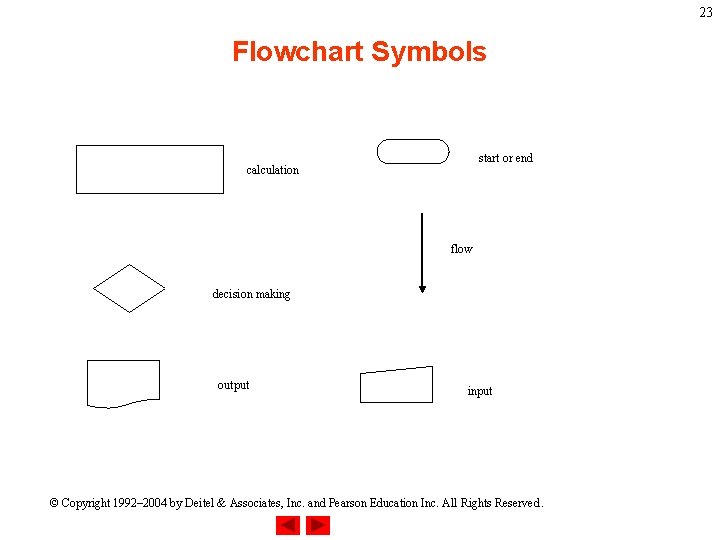
22 2. 3 Flowcharts • Flowchart – Graphical representation of an algorithm – Drawn using certain special-purpose symbols connected by arrows called flowlines – Rectangle symbol (action symbol): • Indicates any type of action – Oval symbol: • Indicates the beginning or end of a program or a section of code • Single-entry/single-exit control structures – Connect exit point of one control structure to entry point of the next (control-structure stacking) – Makes programs easy to build © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

23 Flowchart Symbols start or end calculation flow decision making output input © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

24 Example 2. 3 Foreign Exchange Problem • The amount of $ in your hand makes how meny TL • 1 $ 3. 05 TL • Inputs: : – amount of dollar in your hand • Output: – How much does the dollar worth in terms of TL • : Limitations – 1 dolar is 3. 05 YTL forex rate is constant – just convert to TL © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Ex 2. 13 Algorithm of exchange rate calculation • • 1 Start 2 Define the forex rate 3 Get dollar amount 4 TL correspondence of the dollar is computed – TL = dollar * exchage rate • 5 dsiplay TL • 6 Stop or End • What variables are needed? – dollar, TL – exchange rate? © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved. 25

26 Pseudocode • • 1 Start 2 Set forex. Rate = 3. 05 3 a Display “Enter dollar in your hand” 3 b Input dollar 4 Set tl = dollar * forex. Rate 5 Display “your”, dollar , “makes”, tl 6 Stop or End © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

27 Variables • Forex. Rate – a real number set at the begining – fixed it does not change • dollar – dollar in the hand of the user – real input – every run of the program has a different value • tl – calculated TL amout for the dollar with the dixed forex. Rate © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

28 Limitations and Extensions • Limitations: – every time a new $ is given the algorithme start from begining – if the user enters a negative value it prints a negative NTL – if the user enters a character it fails to compute • Note: – should the exchange rate be asekd as a second input or is it fixed As it is not chaning very often – Exercise: – Modify the algorithm when the for ex rate change as well • Extension of the problem – given NTL the user mey want to chose the forex ohter then dollar to purchase © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

29 Ex 2. 4. Length conversion • What is the equivanent of a given inch in term of cm • Inputs: – inch • Outut: – cm • Limitations: – just between inch and cm • Note: relation between c. m. and inch is constant and 1 inch is 2. 54 cm © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

30 Ex 2. 5. Area and circunference of circle • Given a radius of a circle calcualte its area and circunference • Inputs: – radius • Output: – area and circkunference – Note has two outputs • Limitations: – only for circle • Note: Pi is a universal constant as well 3. 14159 © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

31 Area and Circunference of circle • • 1 Start 2 Set the value of pi = 3. 1416 2 Get radius 4 Compute area and circunference 4. a area = pi * (radius)2 4 b circunf. = 2 * pi * radius 5 display area and circunference to the screen 6 Stop or end • What are variables? – radius, area, circunference • What about pi – its value does not change – universan constant • What are the limitations of the algorithm? © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

32 Pseudocode for Cirlcle • • 1 Start 2 Set pi = 3. 14 3 a Display “Enter radius” 3 b Input radius 4 a Set area = pi * radius 2 4 b Set circunference = 2 * pi * radius 5 a Display “Area of the circle is” , area 5 b Display “Circunference of the circle is”, circunference • 6 Stop © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

33 Ex 2. 7 Display a Fixed message • Display your signiture to the screen • when run always displays your name, last name, address and e-mail to the screen • Limitation: only one signiture for you • No input, no variables • Output Name: Bertan Last name: Badur Address: Bogazici University E-male: badur@boun. edu. tr © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Ex 2. 8 Asking and displaying your personal information • Task: ask name lastname and age • dispay to the screeen • Inputs : name, last. Name – String • age - integer • Output: A messge that change according to your name last name and age but has some fixed characters • Example output • Name: İrem Last Name : Badur Age: 9 & Associates, Inc. and Pearson Education Inc. All Rights Reserved. © • Copyright 1992– 2004 by Deitel 34

35 Algorithm • 1 Start • 2 Ask and get name, last name and age of a person • 2 a ask and get neme • 2 b ask and get last name • 2 c ask and get age • 3 Dispay personal information in a forfmated way to the screen • 3 a dispay name • 3 b dispay last name • 3 c dispay age • 4 Stop © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

36 Pseudocode • • • 1 Start 2 a i Display “Enter your name” 2 a ii Input name 2 b i Display “Enter your last name” 2 b ii Input last. Name 2 c i Display “Enter your age” 2 c ii Input age 3 a Display “Name: ” , name 3 b Display “Last Name: ”, last. Name 3 c Display “Age: ”, age 4 Stop © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

37 Variables • name , last. Name – String – set of characters • age – integer your age © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

38 Flowchart • Draw the flowchart © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

39 Ex 2. 9. Exam grades • Computes exam statistics • Inputs: – student grades • Outputs: – avgerage, min, max, letter grades, . . . • Limits: – only for one exam © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

A Simple Grade Average Calculation Problem • Task: There are only three students in a class • Ali, Ahmet and Nazlı. Get their exam grades from the user and calculate and display the class average to the screen. © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

41 Algorithm • A class consisting of three students: Ali, Ahmet, Nazlı 1 Start 2 Get Ali’s grade 3 Get Ahmet’s grade 4 Get Nazlı’s grade 5 Compute the average grade Average grade = (Ali’s grade + Ahmet’s grade + Nazlı’s grade)/3 6 Display the average grade 7 End • Variables: – Ali’s grade, Ahmet’s grade, Nazlı’s grade, – average grade © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Pseudocode and variables 1 Start 2 a Declare Integer alis. Grade 2 b Declare Integer ahmets. Grade 2 c Declare Integer nazlis. Grade 2 d Declare Real average 3 a Display “Enter Ali’s grade” 3 b Input alis. Grade 4 a Display “Enter Ahmet’s grade” 4 b Input ahmets. Grade 5 a Display “Enter Nazli’s grade” 5 b Input nazlis. Grade © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Pseudocode and variables (cont. ) 6 Set average = (alis. Grade + ahmets. Grade + nazlis. Grade)/3 7 Display “the class average” , average 8 End Variables alis. Grade, ahmets. Grede and nazlis. Grade are declared as integers average is declared as Real Note if implemented in Java sum of three integers is an integer dividing by 3 you may lose the remainder because of ineger division © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Solution • Declare the student grades as Real variables average = ( 10. 0 + 9. 0) / 3 here average is 9. 33333 • if grades are declared as integers average = (10 + 9) / 3 here average is 9. 00000 © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Another Important feature • In step 6 of the pseudocode • average can be computed in one asignment statement • or it can be computed is steps as follows 6 a Set sum = alis. Grade 6 b Set sum = sum + ahmets. Grade 6 c Set sum = sum + nazlis. Grade 6 d average = sum / 3 How do you get rid of the information lose due to integer division ? © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

46 Ex 2. 10. Purchase • what is total payment after a sale • Inputs: – products SKU and amounts • Outut: – invoice total payment value added tax • Note prices of goods are not inputs © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

47 Purchase Problem tasl • two products apple and pair – prices are given not chaning • Value added tax – tax rate is constant • Input: – Amout. Apple, Amount. Pair – asked to user • Output: – net. Pay, VAT, gross. Pay – calculated and printed • Variables: – – Price. Apple, Price. Pair – fixed Amout. Apple, Amount. Pair – asked to user VAT Rate – fixed net. Pay, VAT, gross. Pay – calculated and printed © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

48 Purchase Problem Algorithm • 1 Start • 2 a define prices for the two goods – Price. Apple = 4, Price. Pair = 5 • 2 b define value added tax rate – VATRate = 0. 18 • 3 get amount of apple and pair purchased from the user • 4 Calculate net payment – net. Pay = Price. Apple*Amount. Apple + Price. Pair*Amount. Pair • 5 Calculate VAT – VAT ? net. Pay*VATRate • 6 Calculate gross payment – gross. Pay = net. Pay + VAT • 7 print net psyment, VATand total payment to screen • 8 End © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

49 pseudocode flowchart • Exercise to you • Note if you are sure that value of a variable will not change through out the program, • you can declare them a constants • many programming languages including Java has a syntax for constants • any attempt to change the value of a constant is a syntax error • Examples of well known constants pi = 3. 1416, e = 2. 713 speed of light, Avagadro number © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Constants in pseudocodes • Constant Integer price. Apple = 4 • Constant Real pi = 3. 14 © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

51 Notes Purchase Problem • Note that • calculating net Paymnet can be performed in two steps as – 4 a net. Pay = Price. Apple*Amount. Apple – 4 b net. Pay = net. Pay + Price. Pair*Amount. Pair © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

52 Ex 2. 11. Tax Calculation • Compute the tax burden • Inputs: – yearly income • Output: – tax burden • Note: tax rate is given © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

53 Ex. 2. 12 Interest calculation • Depositing some money calculate interest earned on that • Inputs: – Principle – term – yearly interest rate • Output: – money – interest earned : © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

54 Exercise • Suppose a language does not support mode • In Java mode is implemented by % – 14 % 3 = 2 – 12 % 3 = 0 • How do you imlement mode if it is not supported by the language syntax © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

55 Solution • Mode opperation give the remainder • Ex 10 mode 3 = 1 • 9 mode 3 = 0 • Suppose mode is not supported by the syntax of a programming labnguage • How would you imlement mode? • Set modeab = a mode b • Set modeab = a – (a / b) * b • E. g. : if a = 8, b = 3 a mode b = 8 node 3 = 2 a – (a / b) * b = 8 – (8 / 3) * 3 = 8 – 2*3 = 2 © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

Ex 2. 13 ATM Problem • Consider a customer intending to withdraw money from an ATM, enters the amount she wnnt to withdrow • available types of notes are say: – 100, 50, 20, 10. . . – assume ATM pays as much 100 as possible then pays the remaining with 50 s and so on • Write the algorithm of money withdrawing problem. How much of the money is paid with what type of notes • and remainging money that can not be paid at all • E. g. : 643 TL is paid with • 6 100 s, 0 50 s, 2 20 s and 3 TL can not be paid © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

ATM Problem Hint • Hint: at each step try to identify how much of the money is paid with say by 100 s and what is the remaining amount © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

58 ATM Input and outputs • Input: – money from the user • Output: – – how many 100 TL how many 50 TL how many 20 TL how much not paid © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

59 ATM: Algorithm • • • 1 Start 2 Get money from the user 3 a Determine how many 100 s are paid 3 b Determine remaining money not paid by 100 s 4 a Determine how many 50 s are paid 4 b Determine remaining not paid by 50 s 5 a Determine how many 20 s are paid 5 b Determine how remaining not paid by 20 s 6 Determine money that can not be paid at all 7 Display the results 8 End © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

60 ATM: variables • Variables – input - money – output - how. Many 100, how. Many 50, how. Many 20, not. Paid – remaining - used for intermediate calculations © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

61 Pseudocode of Step 3 a and 3 b • 3 a determine how many 100 s are paid • 3 b determine remaining money not paid by 100 s – remaining = money – 3 a how. Many 100 = remaining / 100 – 3 b remaining = remaining mode 100 • • Example suppose money is 455 remaining = money: remaining becomes 455 how. Many 100 = 455 / 100 = 4 – integer division remaining = remaining mode 100 – remaining becomes 55 © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

62 Exercise • Complete the pseudocode • Draw the flowchart • Write the Java program © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

63 Exercise Time expression 1 • Given a duration of time in hours, munite and seconds expres it in total seconds • E. g. : given 2 hours, 3 minutes and 5 seconds it is 7385 seconds given 2 hours, 0 munites and 30 seconds it is 7230 seconds given 0 hours, 20 munites and 40 seconds it is 1240 seconds © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

64 Exercise: Time expresion 2 Given a duration of time in seconds Expres it in hours, munite and seconds E. g. : given 7385 seconds it is: 2 hours, 3 minutes and 5 seconds given 7230 seconds it is 2 hours, 0 munites and 30 seconds given 1240 seconds it is 0 hours, 20 munites and 40 seconds © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

65 Exercise: Exchange of values of variables • • Given two int type variables a, b hodling values E. g. : a = 5, b = 10 Change their values At the end of the change a becomes 10 , b becomes 5 i) By using a temporary variable İi) Without using a temporary variable © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

66 Exercise: Reverse of an Integer • Given a three digit integer – Examples: 174, 810, 400, 956 • print it in reverse order – Examples 174 to 471, 956 to 659, 400 to 4, 810 to 18 • Hint: : try to get its first digit, second digit and third digit • then try to construct the reverse number © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

67 Input and output • Input: – a three digit integer from the user • Output: – its reverse © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

68 Algorithm 1 • • • 1 Start 2 get number from user 3 determine ones 4 determine tens 5 determine hundrends 6 compute reverse as – reverse = 100*hundreds+10*tens+ones • 7 Display reverse to the screen • 8 End © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

69 Variables for Algorithm 1 • Variables – number– input from user – reverse – output to screen – ones, tens, hundreds, remaining © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

70 Hard of the Algorithm 1 • Set remaining = number // take a copy of number • 3 determine ones: 3 a Set ones = remaining mode 10 3 b Set remaining = remaining / 10 • Example: – – number is 743 remaing is 743 ones is 743 mode 10 = 3 remaining is 743 / 10 74 • perform step 4 amd 5 to find tens and hudereds © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

71 Algorithm 2 • • • 1 Start 2 get number from user 3 determine hundrends 4 determine tens 5 determine ones 6 compute reverse as – invnumber = 100*hundreds+10*tens+ones • 7 Display reverse • 8 end © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

72 Algorithm 2 • Set remaining = number // copy of money • 3 determine hundreds: 3 a Set hundreds = remaining / 100 3 b Set remaining = remaining mode 100 • Example: – – number is 743 remaing is 743 hundreds is 743 / 100 = 7 remaining is 743 mode 100 = 43 • perform step 4 amd 5 to find tens and ones © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

73 Algorithm 3 • • • 1 Start 2 initialize reverse to zero 3 get number from user 4 a determine ones 4 b update remainder 4 c update reverse 5 a determine tens 5 b update remainder 5 c update reverse © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

74 Algorithm 3 (contg. ) • • • 6 a determine hundrends 6 b update remainder 6 c update reverse 7 print reverse 8 end © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

75 Hard of Algorithm 3 • • initially reverse variable is set to 0 4 a determine ones: Set ones = remaining mode 10 4 b update remainder Set remaining = remaining / 10 4 c updata reverse Set reverse = 10*reverse + ones // inverse becomes ones © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.

76 Hard of Algorithm 3 • • just before 5 inverse is ones 5 a determine tens: Set tens = remaining mode 10 5 b update remainder Set remaining = remaining / 10 5 c updata reverse Set reverse = 10*reverse + tems // inverse becomes ones © Copyright 1992– 2004 by Deitel & Associates, Inc. and Pearson Education Inc. All Rights Reserved.