Mirror and Magnification Equations The Mirror Equation The

Mirror and Magnification Equations

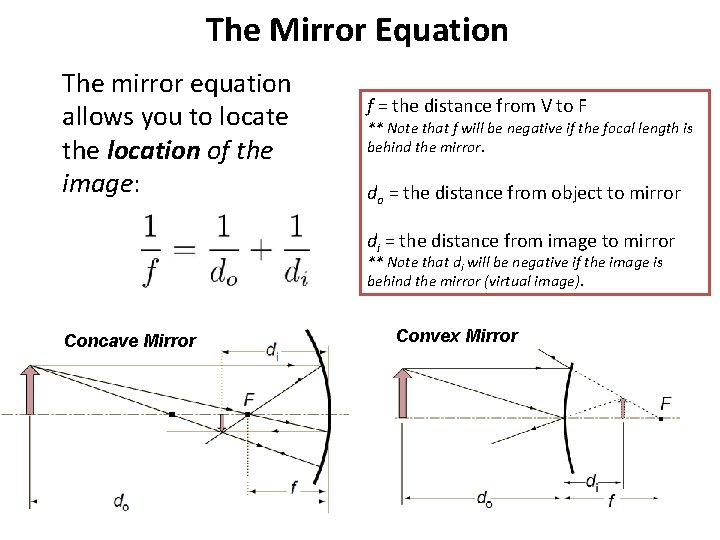
The Mirror Equation The mirror equation allows you to locate the location of the image: f = the distance from V to F ** Note that f will be negative if the focal length is behind the mirror. do = the distance from object to mirror di = the distance from image to mirror ** Note that di will be negative if the image is behind the mirror (virtual image). Concave Mirror Convex Mirror

The Magnification Equation • Tells you the change in size, or height (the magnification) of the image relative to the object using the object and image distances from the mirror. • The magnification (m) is given by the formula: m = magnification ho = the height of the object hi = the height of the image ** Note that hi will be negative if the image is inverted (below the principal axis) compared to the object.

Summary of Mirror and Magnification Equations • All distances are measured from the vertex of a curved mirror. • Distances of real objects and images (in front of mirror) are positive. • Distances of virtual objects and images (behind the mirror) are negative. • Object and image heights are positive when measured above the principal axis and negative when measured below the principal axis.

When doing calculations. . . • List the givens and required’s. • Show all of your work, including the formulas, substituted values and final answer with a unit. • A descriptive concluding statement is absolutely necessary.

Practice Problem 1 A convex mirror has a focal length of − 20 cm. An object with a height of 0. 40 m is placed 30 cm from the mirror. a) Calculate the image distance b) Calculate the image height Givens: b) a) f = − 20 cm ho = 40 cm do = 30 cm Required: a) di = ? b) hi = ? The distance of the image is 12 cm. It is virtual and behind the mirror. The height of the image is 16 cm. The image is upright.

Practice Problem 1 A concave mirror with a 12 cm focal length has a candle 2. 5 cm tall placed in front of the mirror, 40 cm from the vertex. a) Calculate the image distance. b) What is the magnification of the image? Givens: b) a) f = 20 cm ho = 5 cm do = 15 cm Required: a) di = ? b) m = ? The distance of the image is about 17 cm. The image is real and in front of the mirror. On your calculator, you can input 0. 058333 and press 1/x to get the reciprocal Magnification is negative so image is inverted. It is 0. 425 times smaller than object.