MIQP formulation for optimal controlled variable selection in

MIQP formulation for optimal controlled variable selection in Self Optimizing Control Ramprasad Yelchuru Prof. Sigurd Skogestad MIQP - Mixed Integer Quadratic Programming Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 1/16

Outline 1. Motivation 2. Problem formulation 3. MIQP formulation 4. Evaporator Case study 5. Comparison of MIQP & customized BAB 6. Conclusions Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 2/16
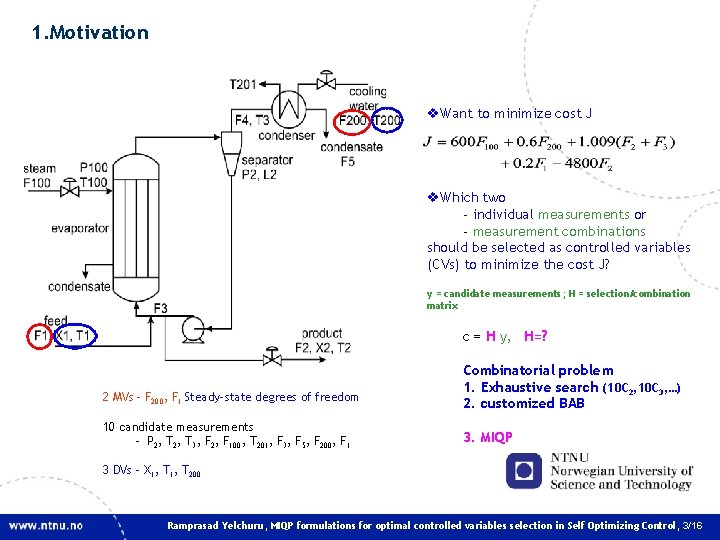
1. Motivation v. Want to minimize cost J v. Which two - individual measurements or - measurement combinations should be selected as controlled variables (CVs) to minimize the cost J? y = candidate measurements; H = selection/combination matrix c = H y, H=? 2 MVs – F 200, F 1 Steady-state degrees of freedom 10 candidate measurements – P 2, T 3, F 2, F 100, T 201, F 3, F 5, F 200, F 1 Combinatorial problem 1. Exhaustive search (10 C 2, 10 C 3, …) 2. customized BAB 3. MIQP 3 DVs – X 1, T 200 Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 3/16
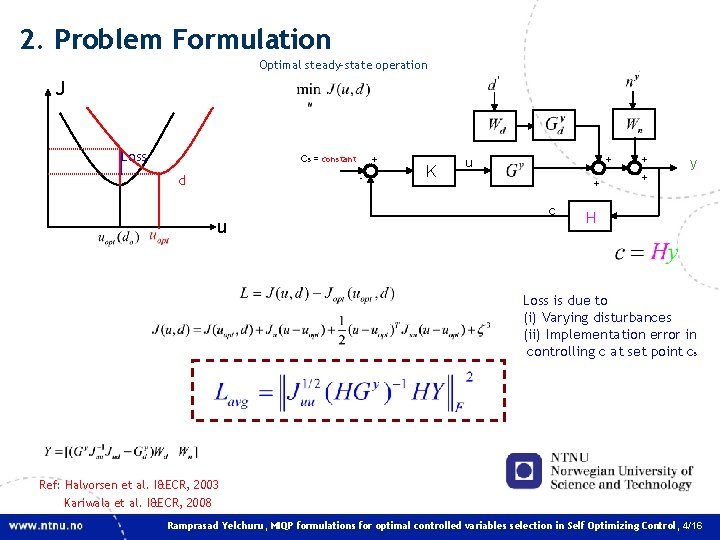
2. Problem Formulation Optimal steady-state operation J Loss cs = constant d + - u K u + + c + y + H Loss is due to (i) Varying disturbances (ii) Implementation error in controlling c at set point cs Ref: Halvorsen et al. I&ECR, 2003 Kariwala et al. I&ECR, 2008 Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 4/16
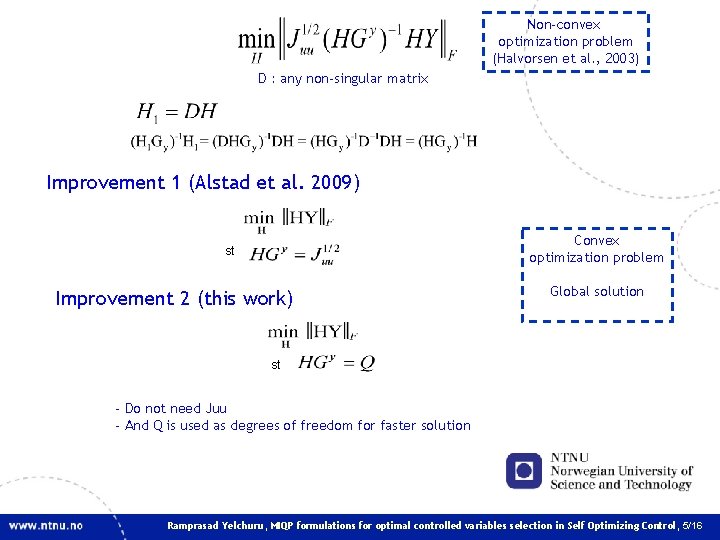
Non-convex optimization problem (Halvorsen et al. , 2003) D : any non-singular matrix Improvement 1 (Alstad et al. 2009) Convex optimization problem st Improvement 2 (this work) Global solution st - Do not need Juu - And Q is used as degrees of freedom for faster solution Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 5/16
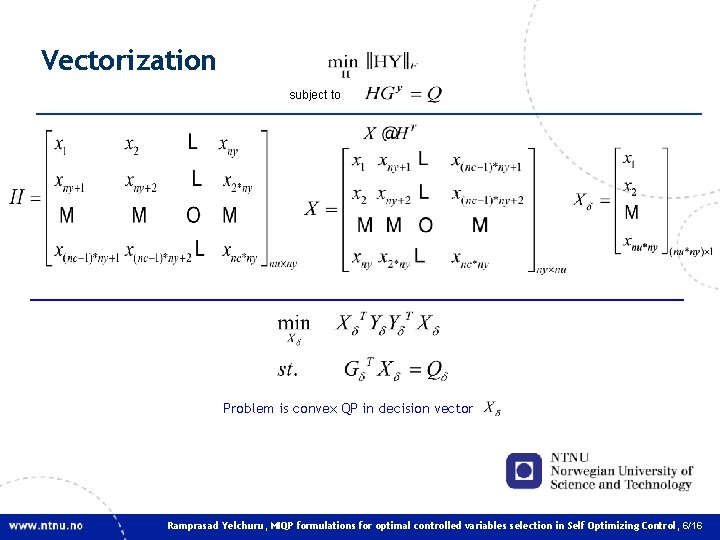
Vectorization subject to Problem is convex QP in decision vector Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 6/16

Controlled variable selection st. Optimization problem : Minimize the average loss by selecting H to obtain CVs as (i) best individual measurements (ii) best combinations of all measurements (iii) best combinations with few measurements Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 7/16

3. MIQP Formulation Big M approach high value M => high cpu time We solve this MIQP for n = nu to ny Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 8/16
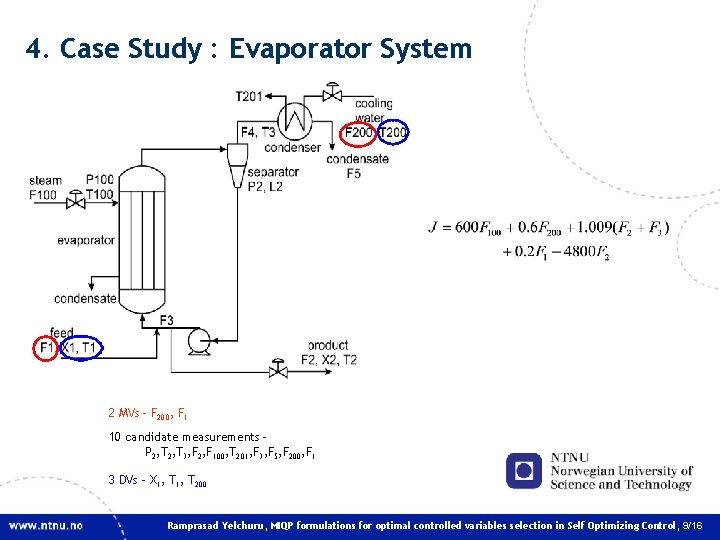
4. Case Study : Evaporator System 2 MVs – F 200, F 1 10 candidate measurements – P 2, T 3, F 2, F 100, T 201, F 3, F 5, F 200, F 1 3 DVs – X 1, T 200 Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 9/16

Case Study : Results Data Results Controlled variables (c) Optimal individual measurements Loss 2 = 3. 7351 Optimal 4 measurement combinations Loss 4 = 0. 4515 Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 10/16
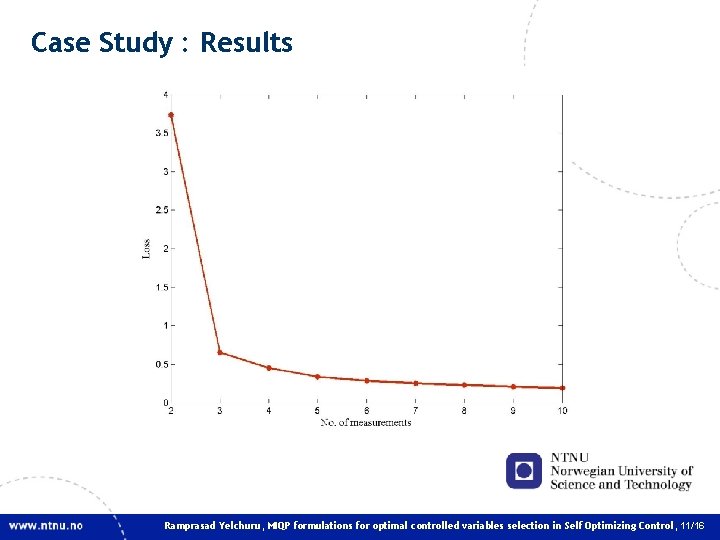
Case Study : Results Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 11/16
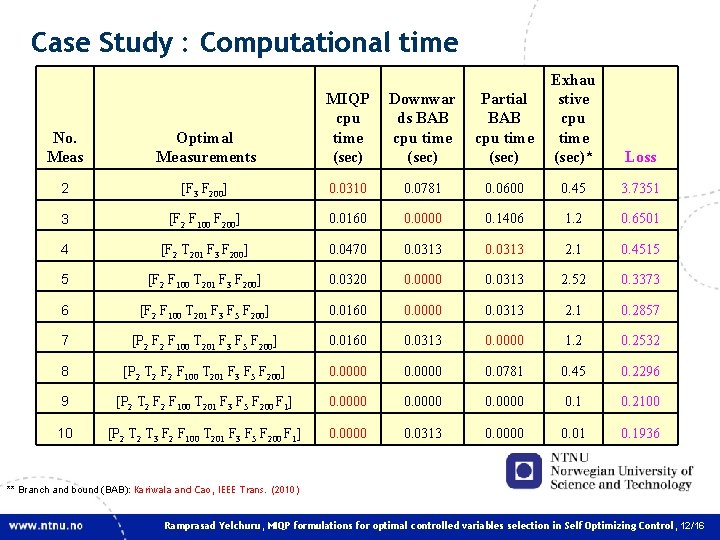
Case Study : Computational time Downwar ds BAB cpu time (sec) Partial BAB cpu time (sec) Exhau stive cpu time (sec)* No. Meas Optimal Measurements MIQP cpu time (sec) 2 [F 3 F 200] 0. 0310 0. 0781 0. 0600 0. 45 3. 7351 3 [F 2 F 100 F 200] 0. 0160 0. 0000 0. 1406 1. 2 0. 6501 4 [F 2 T 201 F 3 F 200] 0. 0470 0. 0313 2. 1 0. 4515 5 [F 2 F 100 T 201 F 3 F 200] 0. 0320 0. 0000 0. 0313 2. 52 0. 3373 6 [F 2 F 100 T 201 F 3 F 5 F 200] 0. 0160 0. 0000 0. 0313 2. 1 0. 2857 7 [P 2 F 100 T 201 F 3 F 5 F 200] 0. 0160 0. 0313 0. 0000 1. 2 0. 2532 8 [P 2 T 2 F 100 T 201 F 3 F 5 F 200] 0. 0000 0. 0781 0. 45 0. 2296 9 [P 2 T 2 F 100 T 201 F 3 F 5 F 200 F 1] 0. 0000 0. 1 0. 2100 10 [P 2 T 3 F 2 F 100 T 201 F 3 F 5 F 200 F 1] 0. 0000 0. 0313 0. 0000 0. 01 0. 1936 Loss ** Branch and bound (BAB): Kariwala and Cao, IEEE Trans. (2010) Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 12/16

5. Comparison of MIQP, Customized Branch And Bound (BAB) methods v MIQP formulations can accommodate wider class than monotonic functions (J) v MIQPs are solved using standard cplex routines v MIQPs are simple and are easy to incorporate few structural constraints v MIQPs are computationally intensive than BAB methods v Single MIQP sufficient for problems formulation is the described v Customized BAB methods can handle only monotonic cost functions (J) v Customized routines are required v BABs require a deeper understanding of the customized routines to solve problems with structural constraints v Computationally faster than MIQPs as they exploit the monotonic properties efficiently v Monotonicity of the measurement combinations needs to be checked before using PB 3 for optimal measuement subset selections Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 13/16
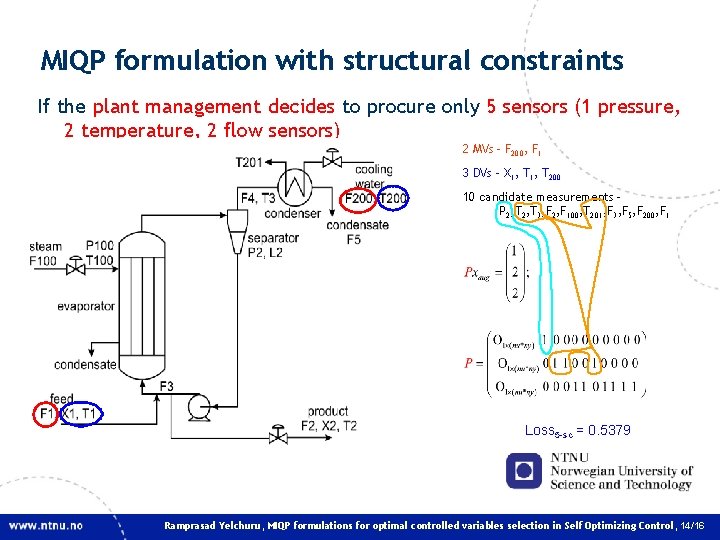
MIQP formulation with structural constraints If the plant management decides to procure only 5 sensors (1 pressure, 2 temperature, 2 flow sensors) 2 MVs – F 200, F 1 3 DVs – X 1, T 200 10 candidate measurements – P 2, T 3, F 2, F 100, T 201, F 3, F 5, F 200, F 1 Loss 5 -sc = 0. 5379 Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 14/16

6. Conclusions v The self optimizing control non-convex problem is reformulated as convex problem v MIQP based formulation is presented for § § § Selection of CVs as optimal individual measurements Selection of CVs as combinations of all measurements Selection of CVs as combinations of optimal measurement subsets v MIQPs are more simple, intuitive and are easy compared to customized Branch and Bound methods v MIQPs are computationally intensive than customized Branch and Bound methods Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 15/16

Ramprasad Yelchuru, MIQP formulations for optimal controlled variables selection in Self Optimizing Control, 16/16
- Slides: 16