Minkowski Sums and Offset Polygons Ron Wein Computing

Minkowski Sums and Offset Polygons Ron Wein

Computing Minkowski Sums

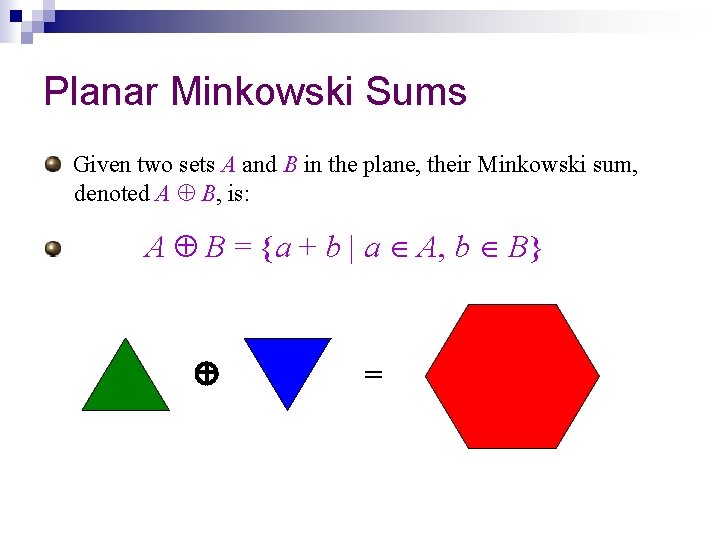
Planar Minkowski Sums Given two sets A and B in the plane, their Minkowski sum, denoted A B, is: A B = {a + b | a A, b B} =

The Sum Complexity (I) We are given two polygons P and Q with m and n vertices respectively. If both polygons are convex, the complexity of their sum is m + n, and we can compute it in (m + n) time using a very simple procedure.

The Sum Complexity (II) If only one of the polygons is convex, the complexity of their sum is (mn). If both polygons are non-convex, the complexity of their sum is (m 2 n 2).

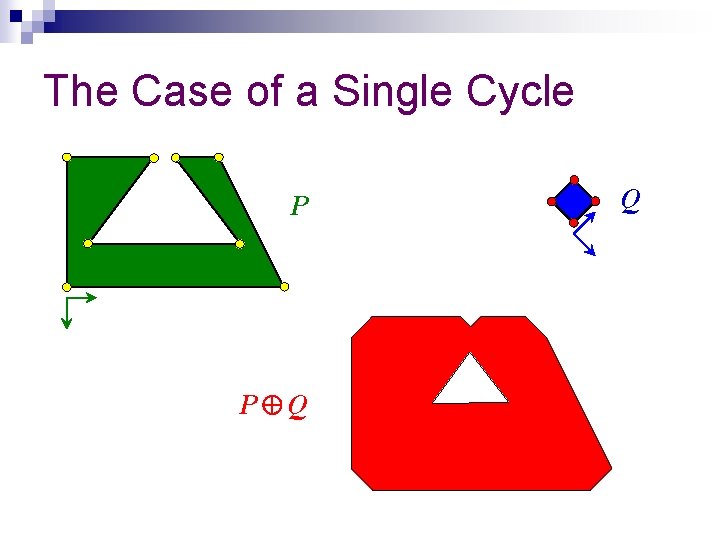
The Decomposition Method The prevailing method for computing the sum of two nonconvex polygons: Decompose P and Q into convex subpolygons, compute the pair-wise sums of the sub-polygons and obtain the union of these sums. P 1 PP 2 Q 1 Q Q 2 P Q

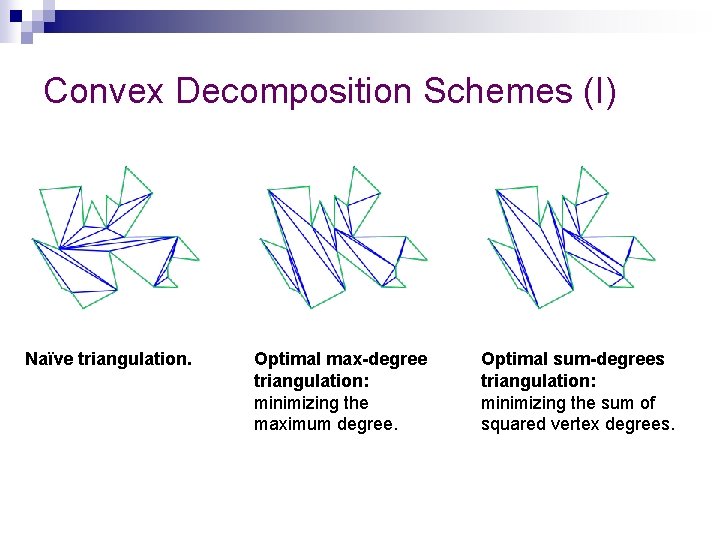
Convex Decomposition Schemes (I) Naïve triangulation. Optimal max-degree triangulation: minimizing the maximum degree. Optimal sum-degrees triangulation: minimizing the sum of squared vertex degrees.

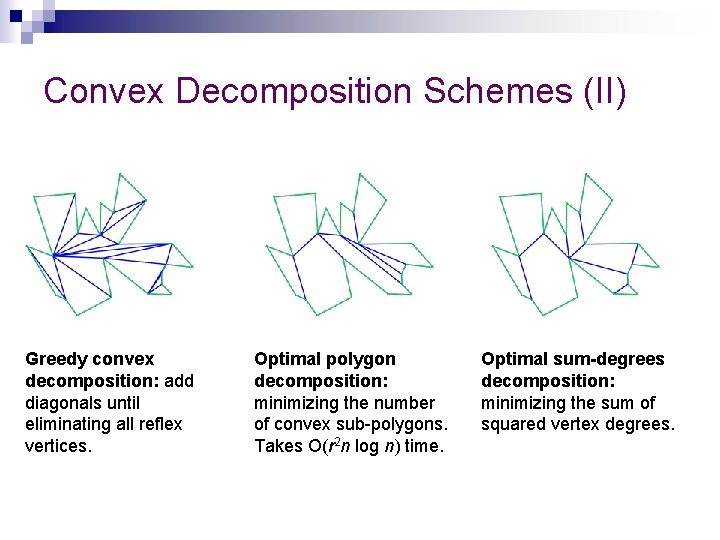
Convex Decomposition Schemes (II) Greedy convex decomposition: add diagonals until eliminating all reflex vertices. Optimal polygon decomposition: minimizing the number of convex sub-polygons. Takes O(r 2 n log n) time. Optimal sum-degrees decomposition: minimizing the sum of squared vertex degrees.

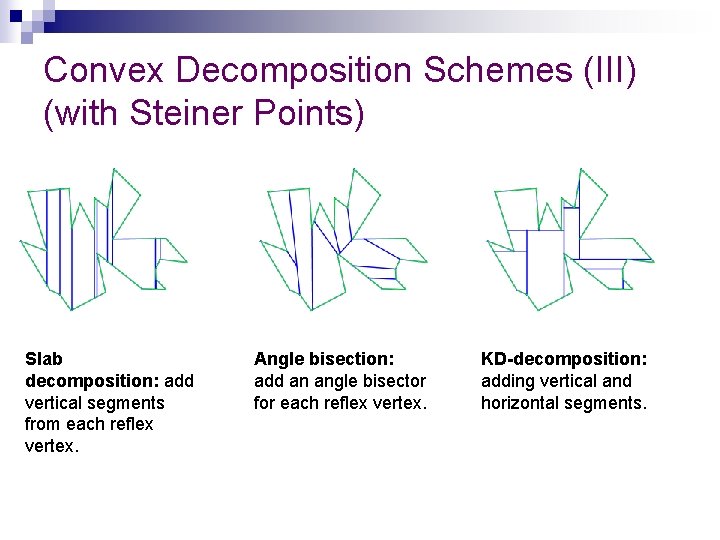
Convex Decomposition Schemes (III) (with Steiner Points) Slab decomposition: add vertical segments from each reflex vertex. Angle bisection: add an angle bisector for each reflex vertex. KD-decomposition: adding vertical and horizontal segments.

Computing the Union Given a set of polygons S 1, …, SM with counterclockwise (positive) orientation, construct the arrangement of their edges. Set N(fu) = 0 for the unbounded face fu. Then compute N(f ) for each other face using a simple BFS traversal. All faces with N(f ) > 0 contribute to the union. (1) (2) (0) (1) (2) (1)

Convolution of Planar Tracings (Guibas, Ramshaw and Stolfi, 1983) A planar tracing T comprises a continuous set of points. Each point t T is associated with a direction dir(t). The convolution of two planar tracings S and T, denoted S T, comprises the pair-wise sum of all points s S and t T such that dir(s) = dir(t). t s S T

Convolution of Polygons (I) A polygonal tracing P consists of moves (going along an edge in a fixed direction), and turns (rotating at a vertex). For a vertex p of P, dir(p) is a continuous range of directions. The convolution P Q therefore contains the sum of each edge of the polygonal tracing Q, whose direction is in dir(p), with p. P dir(p) p Q

Convolution of Polygons (II) At the worst case, the convolution of two polygons P Q consists of (mn) line segments. Guibas and Seidel (1987) gave an output-sensitive algorithm for computing the convolution segments in O(m + n + K) time. The convolution segments form closed cycles. The Minkowski sum P Q contains all points whose winding number with respect to any of the convolution cycles is positive. (0) (1) (2) (0)

The Case of a Single Cycle Q P 2 P Q 0 0 2 2 1

The Case of Multiple Cycles We compute the first cycle, starting from the two bottommost vertices in P and Q. If P or Q are convex, we are done. Otherwise, while it is possible to locate two vertices p P and q Q that should be in the convolution, construct an additional convolution cycle.

The Minkowski-Sum Package of CGAL

The CGAL Arrangement Package Supports the construction of maintenance of 2 D arrangements – planar subdivisions induced by a set of planes. Handles a variety of curves. Each family of curves (line segments, poly-lines, circular arcs, conic arcs, etc. ) is handled by a geometric traits-class. Handles degenerate cases robustly and accurately, relying on the exact computation paradigm. Common intersection points Tangency points

The Decomposition Method The Minkowski-sum package re-implements the robust algorithms for sum-computations using the convex polygondecomposition method (Agarwal, Flato and Halperin, 2000). Available decomposition methods: Implemented in the Partition_2 package Optimal. Hertel-Mehlhorn’s approximation scheme. Greene’s approximation scheme. The small-side angle-bisector approximation scheme.

The Convolution Method The first software that robustly implements the convolution algorithms for polygons. Uses the same infrastructure for multi-way polygon union, used by the decomposition method. The same algorithm also works for the case of closed convolution cycles.

Low-Dimensional Features The Minkowski sum of two polygons may contain lowdimensional features (isolated vertices and antennas). The package can treat them as follows: discard them (output the regularized sum), or give access to them through the underlying arrangement.

Experimental Input Sets (I) stars chain comb fork

Experimental Input Sets (II) cavity random knife country

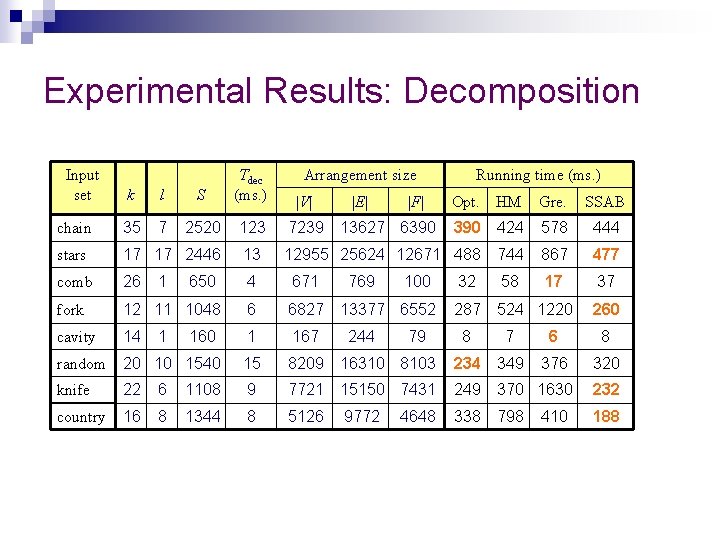
Experimental Results: Decomposition Input set k l S Tdec (ms. ) chain 35 7 2520 123 7239 stars 17 17 2446 13 comb 26 4 671 fork 12 11 1048 6 6827 cavity 14 1 167 random 20 10 1540 15 8209 knife 22 6 1108 9 country 16 8 1344 8 1 1 650 160 Arrangement size |V| |E| |F| Running time (ms. ) Opt. HM Gre. SSAB 390 424 578 444 12955 25624 12671 488 744 867 477 32 58 17 37 287 524 1220 13627 6390 769 100 13377 6552 244 79 260 8 7 6 8 16310 8103 234 349 376 320 7721 15150 7431 249 370 1630 232 5126 9772 338 798 188 4648 410

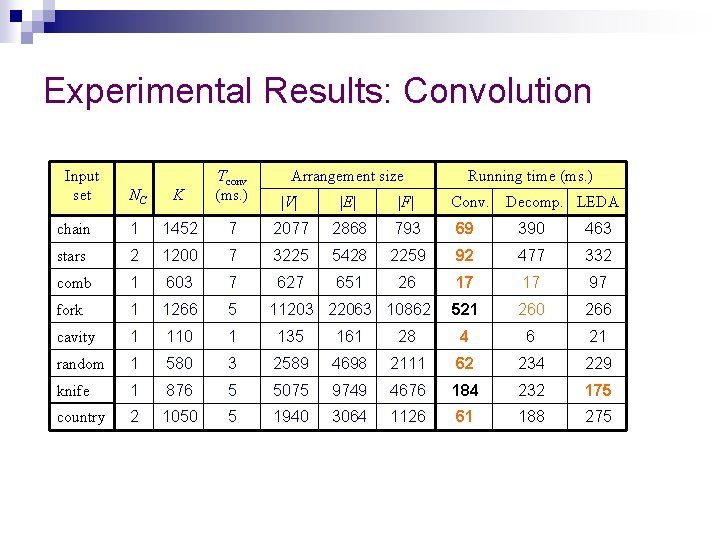
Experimental Results: Convolution Input set NC K Tconv (ms. ) Arrangement size chain 1 1452 7 2077 2868 793 69 390 463 stars 2 1200 7 3225 5428 2259 92 477 332 comb 1 603 7 627 651 26 17 17 97 fork 1 1266 5 521 260 266 cavity 1 110 1 135 161 28 4 6 21 random 1 580 3 2589 4698 2111 62 234 229 knife 1 876 5 5075 9749 4676 184 232 175 country 2 1050 5 1940 3064 1126 61 188 275 |V| |E| |F| 11203 22063 10862 Running time (ms. ) Conv. Decomp. LEDA

Polygon Offsetting

Polygon Offsetting using the Convolution Method Br P 2 Computing the induced convolution cycle arrangement and P the … B r winding numbers … 0 0 2 2 1

Related Traits Classes Computing the sum of two polygons (objects of the type Polygon_2<Kernel>) is of course performed using the Arr_segment_traits_2<Kernel> class and using exact rational arithmetic. In case of offsetting we should consider the following traits classes: Arr_circle_segment_traits_2 – handles line segments and circular arcs using exact rational arithmetic. Arr_conic_traits_2 – handles bounded conic arcs using exact algebraic numbers (based on CORE).

Offsetting a Polygon Edge (I) q 2 p 2 = (x 2, y 2) q 1 = - 90º p 1 = (x 1, y 1)

Offsetting a Polygon Edge (II) If the line supporting p 1 p 2 is ax + by + c = 0, then the line supporting q 1 q 2 is ax + by + (c + ℓr) = 0. Problem: In the general case, offset arcs are not supported by rational lines! Solution no. 1: Represent the offset edge as a segments of a (degenerate) conic curve with rational coefficients:

Our Approximation Scheme 1. Find ’ 1 and ’ 2 such that sin( ’j), cos( ’j) are rational. 2. Compute q’j = (xj + r cos( ’j) , yj + r sin( ’j) ). 3. Compute the intersection q’ of the two tangents at q’ 1 and q’ 2. Use the polyline q’ 1 q’q’ 2 as an approximation. q’ 2 q’ q’ 1 ’ 2 ’ 1 p 2 p 1

Computing “Rational” Angles (I) Using the half-angle formulae we have: Observation: If is rational, then sin( ) = 2 / (1+ 2) and cos( ) = (1 - 2) / (1 + 2) are also rational.

Computing “Rational” Angles (II) If x 1 > x 2 we take a rational approximation : If x 1 < x 2 we approximate the edge length from above (that is, we take a rational ). We use the good old Babylonian method for approximating square roots ( ).

The Approximation Quality Lemma: For any polygon edge connecting (x 1, y 1) and (x 2, y 2) whose length is ℓ and any > 0, if we take an approximation of the edge length that satisfies: then the approximation error is bounded by . q’ 2 q’ q’ 1 p 2 p 1

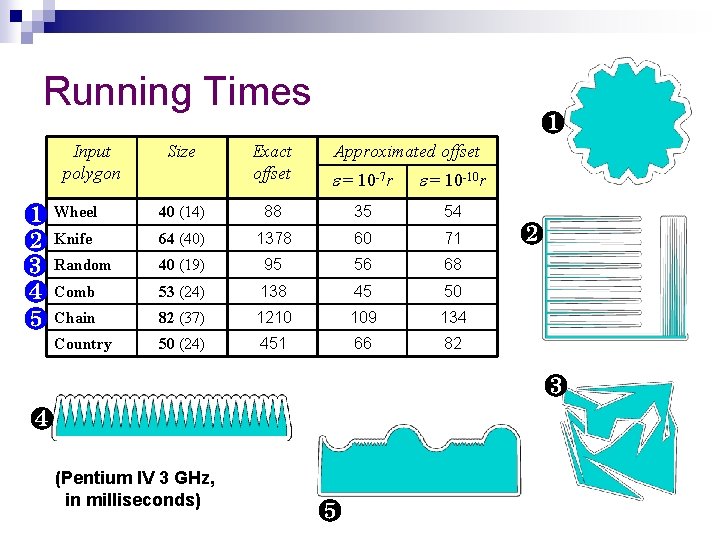
Running Times Input polygon Size ❶ Exact offset Approximated offset = 10 -7 r = 10 -10 r ❶ Wheel ❷ Knife ❸ Random ❹ Comb ❺ Chain 40 (14) 88 35 54 64 (40) 1378 60 71 40 (19) 95 56 68 53 (24) 138 45 50 82 (37) 1210 109 134 Country 50 (24) 451 66 82 ❷ ❸ ❹ (Pentium IV 3 GHz, in milliseconds) ❺

!Thank you