Ministry of Higher Education and Scientific Research AlMustansiriyah







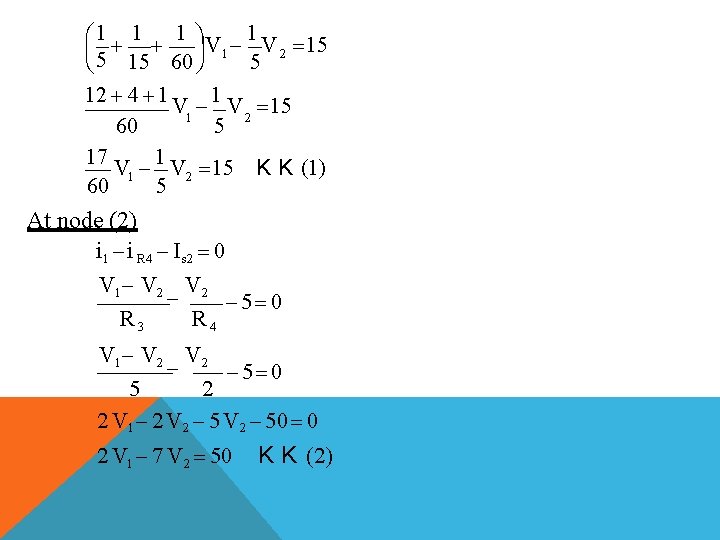








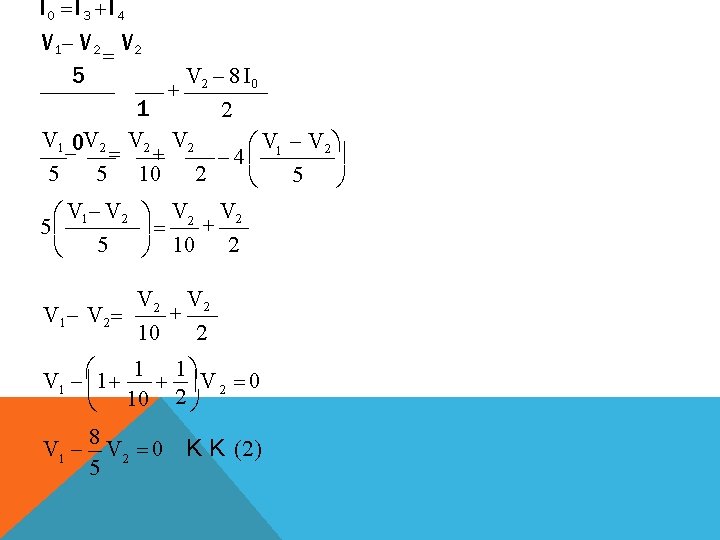












- Slides: 43

Ministry of Higher Education and Scientific Research Al-Mustansiriyah University Faculty of Engineering Computer Engineering Department Electrical Eng. Lab 1' class Assistant Lecturer Hazim alkargole 2017 20189 ﻭﺯﺍﺭةﺎﻟﺘﻌﻠﻴﻢ ﺍﻟﻌﺎﻟﻲ ﻭﺍﻟﺒﺤﺚ ﺍﻟﻌﻠﻤﻲ ﺍﻟﺠﺎﻣﻌﺔ ﺍﻟﻤﺴﺘﻨﺼﺮﻳﺔ ﻛﻠﻴﺔ ﺍﻟﻬﻨﺪﺳﺔ ﻗﺴﻢ ﻫﻨﺪﺳﺔ ﺍﻟﺤﺎﺳﻮﺏ

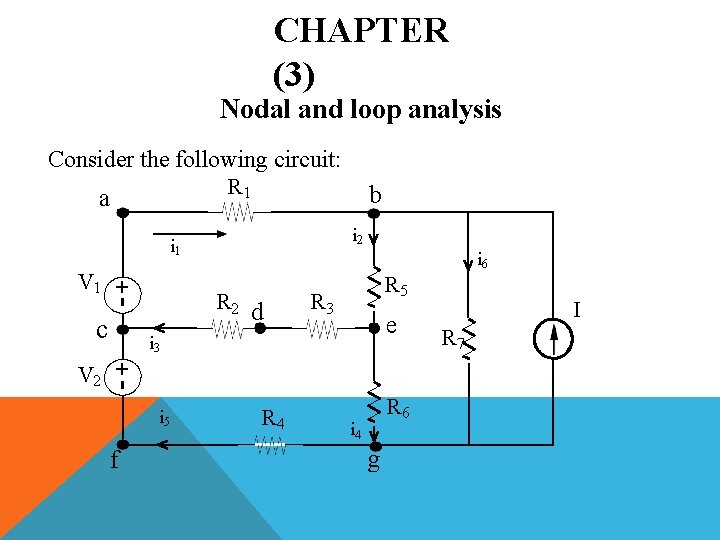
CHAPTER (3) Nodal and loop analysis Consider the following circuit: R 1 a b i 2 i 1 +- V 1 c R 2 d R 5 R 3 e i 3 +- V 2 i 6 i 5 f R 4 R 6 i 4 g I R 7

Definitions: Node : A point where two or more circuit elements join Ex. a, b, c, d, e, f, g Essential Node: A node where three or more circuit element join Ex. b, c, e, g Path: A trace of adjoining elements with no elements included more than once 1. V 1 -R 5 -R 6 2. R 5 -R 6 -R 4 -V 2 , etc

Branch: A path that connects any two nodes. Ex. R 1 , V 1 , R 1 -R 5 , etc Essential Branch: A path that connects two essential nodes without passing through an essential node. Ex. V 1 -R 1 , R 5 , R 2 -R 3 , V 2 -R 4 , … Loop : A path whose last node is the same as its starting node Ex. (1) V 1 -R 5 -R 3 -R 2 (2) V 1 -R 5 -R 6 -R 4 -V 2

Mesh : A loop that doesn’t enclose any other loops. Ex. V 1 -R 5 -R 3 -R 2 Ex. V 2 -R 3 -R 6 -R 4 , … • In chapter (2) we studied circuits containing a single loop or a single node-pair • Such circuits can be solved easily by one algebraic equation. • Here , we will study circuit containing multiple node and multiple loops • Hence we will introduce (2) analysis techniques : 1. Nodal analysis 2. Loop analysis

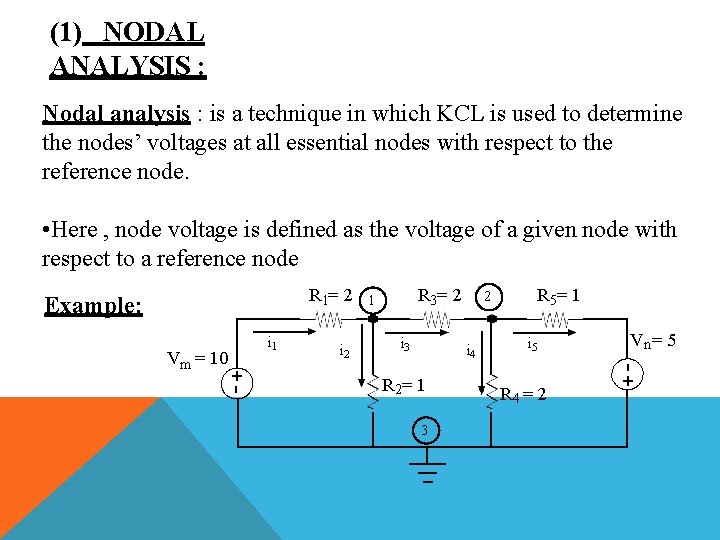
(1) NODAL ANALYSIS : Nodal analysis : is a technique in which KCL is used to determine the nodes’ voltages at all essential nodes with respect to the reference node. • Here , node voltage is defined as the voltage of a given node with respect to a reference node +- Vm = 10 i 1 i 2 R 3= 2 i 3 i 4 R 2= 1 3 R 5= 1 2 i 5 R 4 = 2 Vn = 5 +- R 1= 2 1 Example:

ESSENTIAL NODES : 1, 2, 3 CONSIDER (3) TO BE THE REFERENCE NODE (GROUND) AT (1) APPLY KCL: i 1 i 2 i 3 0 Vm V 1 V V 2 1 0 R 1 R 2 R 3 10 V 1 V 1 V 2 0 2 1 2 V 1 V 2 V 1 5 V 1 0 2 2 2 V 2 5 2 V 1 0 2 4 V 1 V 2 10 K K 1

AT (2) , APPLY KCL: I 3 I 4 I 5 0 V 1 V 2 V 2 Vn 0 R 3 R 4 R 5 V 1 V 2 5 0 2 2 V 1 2 V 2 5 0 2 V 1 4 V 2 10 K K 1 2 4 1 V 1 10 1 4 V 10 2 A V B V A 1 B V 2 2 V 1 2

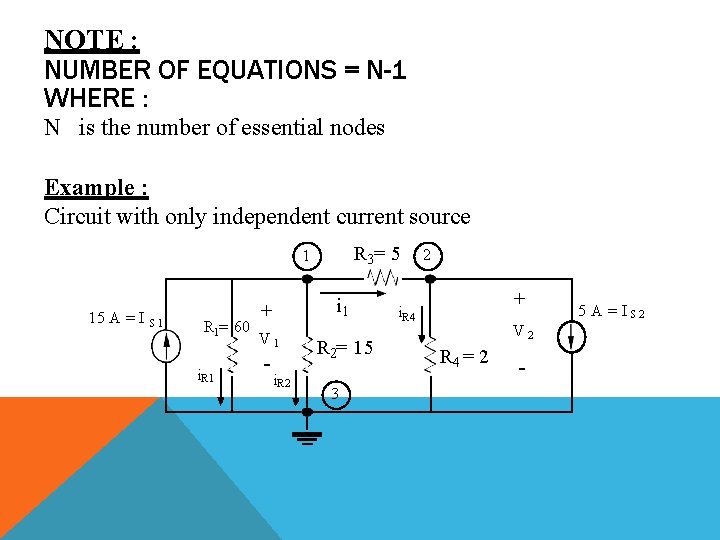
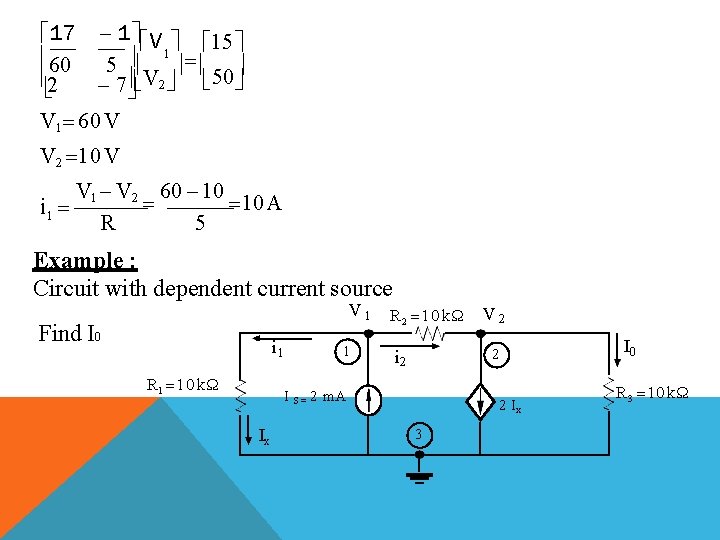
NOTE : NUMBER OF EQUATIONS = N-1 WHERE : N is the number of essential nodes Example : Circuit with only independent current source R 3= 5 1 15 A = I S 1 R 1= 60 i. R 1 i 1 + V 1 - i. R 2= 15 3 2 + i. R 4 V 2 R 4 = 2 - 5 A = I S 2

FIND V 1, V 2 AND I # of essential node = N=3 Select (3) as ground (reference node) # of KCL equations = N-1 = 2 At node (1) apply KCL I s 1 i. R 1 i R 2 i 1 0 V 1 V 1 V 2 0 15 R 1 R 2 R 3 V 1 V 1 V 2 15 0 60 15 5 5
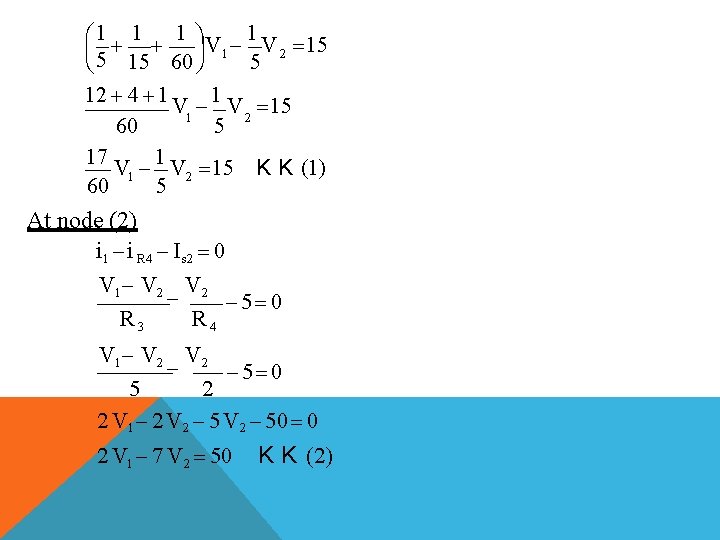
1 1 1 V 1 V 15 1 2 5 5 15 60 12 4 1 1 V 1 V 2 15 60 5 17 1 V 1 V 2 15 K K (1) 60 5 At node (2) i 1 i R 4 Is 2 0 V 1 V 2 5 0 R 3 R 4 V 1 V 2 5 0 5 2 2 V 1 2 V 2 50 0 2 V 1 7 V 2 50 K K (2)

17 1 V 15 1 60 5 2 7 V 2 50 V 1 60 V V 2 10 V V 1 V 2 60 10 A i 1 R 5 Example : Circuit with dependent current source V 1 Find I 0 i 1 R 1 10 kΩ 1 R 2 10 kΩ I 0 2 i 2 I S = 2 m. A Ix V 2 2 Ix 3 R 3 10 kΩ

OF ESSENTIAL NODES = N=3 CHOOSE (3) TO BE REFERENCE NODE ( GROUND ) We have N-1 = 2 KCL equation at node(1) and( 2) At node (1) , apply KCL Is i 1 i 2 0 2 m. A V 1 V 2 0 R 1 R 2 V 1 V 2 2 m. A 10 k 5 k 10 k 0. 2 V 1 0. 1 V 2 2 A K K (1)

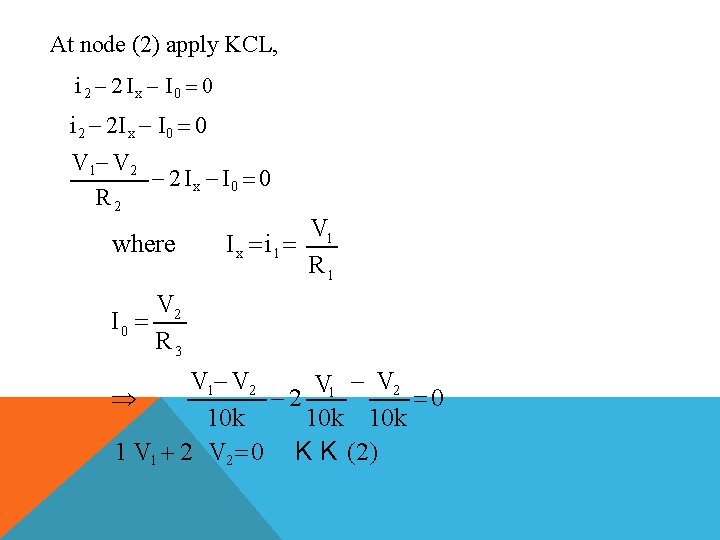
At node (2) apply KCL, i 2 2 Ix I 0 0 i 2 2 I x I 0 0 V 1 V 2 2 Ix I 0 0 R 2 where V 1 I x i 1 R 1 V 2 I 0 R 3 V 1 V 2 V 1 V 2 0 2 10 k 10 k 1 V 1 2 V 2 0 K K (2)

0. 1 V 1 2 2 1 2 V 2 0 V 1 8 V V 2 4 V V 2 4 I 0 0. 4 m A R 3 10 k

EXAMPLE: (CIRCUIT WITH INDEPENDENT VOLTAGE SOURCE) Find ia , ib , ic , id , ie V 1 8Ω 1 ia 2 ic 48 Ω ib N=3 V 2 N-1 = 2 Choose (3) to be ground 20 Ω 3 id 10 Ω ie +- +- 128 18 Ω 70

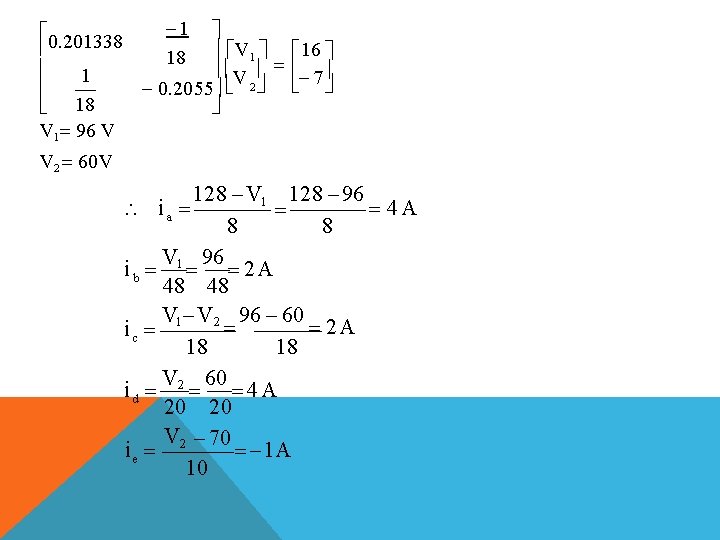
KCL AT (1) 128 V 1 V 1 V 2 0 8 48 18 V V 16 1 1 1 2 0 8 48 18 18 1 0. 201388 V 16 K K (1) 18 KCL at (2) V 1 V 2 V 2 70 0 18 20 10 1 V 1 0. 20555 V 2 7 K K (2) 18

1 0. 201338 18 V 1 16 V 7 1 2 0. 2055 18 V 1 96 V V 2 60 V 128 V 1 128 96 4 A 8 8 V 96 ib 1 2 A 48 48 V 1 V 2 96 60 2 A ic 18 18 V 60 id 2 4 A 20 20 V 2 70 1 A ie 10 ia

128 V 1 128 96 4 A 8 8 V 96 ib 1 2 A 48 48 V V 96 60 2 A ic 1 2 18 18 V 60 id 2 4 A 20 20 V 2 70 1 A ie 10 ia Special case: What if a branch between two essential non-reference node contain a voltage source ? This case is called “super node" case.

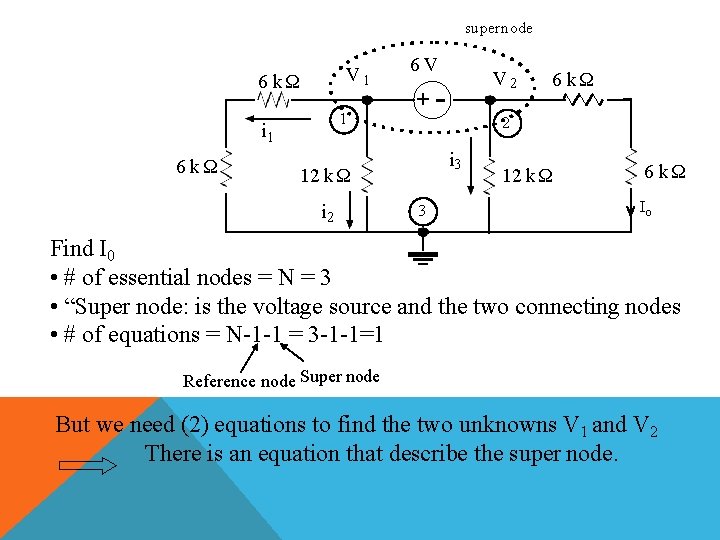
supernode V 1 6 kΩ 1 i 1 6 kΩ 6 V +- 3 6 kΩ 2 i 3 12 k Ω i 2 V 2 12 k Ω 6 kΩ Io Find I 0 • # of essential nodes = N = 3 • “Super node: is the voltage source and the two connecting nodes • # of equations = N-1 -1 = 3 -1 -1=1 Reference node Super node But we need (2) equations to find the two unknowns V 1 and V 2 There is an equation that describe the super node.

APPLY KCL AT THE SUPER NODE : i 1 i 2 i 3 I 0 0 V 1 V 2 0 12 k 12 k V 1 V 2 0 K K (1) 6 k 6 k The super node is described by: V 2 6 V 1 KK(2) 1 1 V 1 0 6 k 6 k V 2 6 1 1 V 1 3 V V 2 3 V I 0 V 2 3 0. 25 m A 12 k

EXAMPLE: CIRCUITS WITH DEPENDENT VOLTAGE SOURCES V 1 2Ω 1 i 1 +- 20 V i 2 5Ω 2 Io 20 Ω 10 Ω 3 Find I 0? N=3 V 2 i 3 N-1 = 2 equations 2Ω i 4 8 Io

KCL AT NODE (1): i 1 i 2 I 0 20 V 1 V 1 V 2 2 20 5 V V 10 1 1 1 2 2 20 5 5 1 1 1 1 V V 2 10 1 5 2 20 5 3 1 V 1 V 2 10 K K (1) 4 5
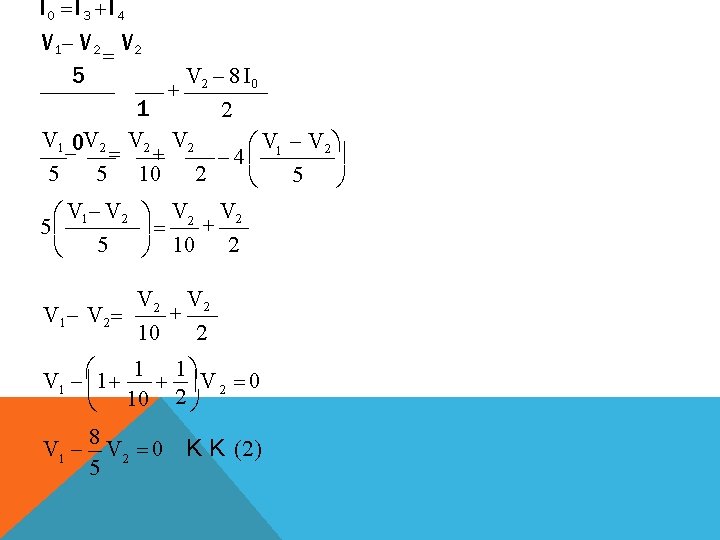
I 0 I 3 I 4 V 1 V 2 5 V 2 8 I 0 1 2 V 1 0 V 2 V 2 V V 2 4 1 5 5 10 2 5 V 1 V 2 5 5 10 2 V 1 V 2 10 2 1 1 V 1 1 V 2 0 10 2 8 V 1 V 2 0 K K (2) 5

3 1 4 5 V 1 10 8 V 2 0 1 5 V 1 16 V V 2 10 V I 0 V 1 V 2 6 1. 2 A 5 5 Loop Analysis (Mesh) Mesh analysis : It is a technique in which KVL is used to determine the current in all meshes # of equations needed = # of meshes = be-(ne-1) Where : be : # of essential branches ne: # of essential nodes

EXAMPLE : 6Ω 2Ω 4Ω + +- Vo i 1 - 8Ω 6 Ω i 3 i 2 Find V 0? We have (3) meshes KVL left loop : 40 2 i 1 8 ( i 1 i 2 ) 0 10 i 1 8 i 2 0 i 3 40 K K (1) +- 40 V 20 V

KVL middle loop: KVL right loop : 8 (I 2 I 1 ) 6 I 2 6 (I 2 I 3 ) 0 8 i 1 20 i 2 6 i 3 0 20 6 (i 3 i 2 ) 4 i 3 0 0 i 1 6 i 2 10 i 3 20 10 8 0 i 1 40 8 20 6 i 0 2 0 6 10 i 3 20 i 1 5. 6 A , i 2 2 A , i 3 0. 8 A V 0 8( i 1 i 2 ) 8 (5. 6 2) 8 (3. 6) V 0 28. 8 V

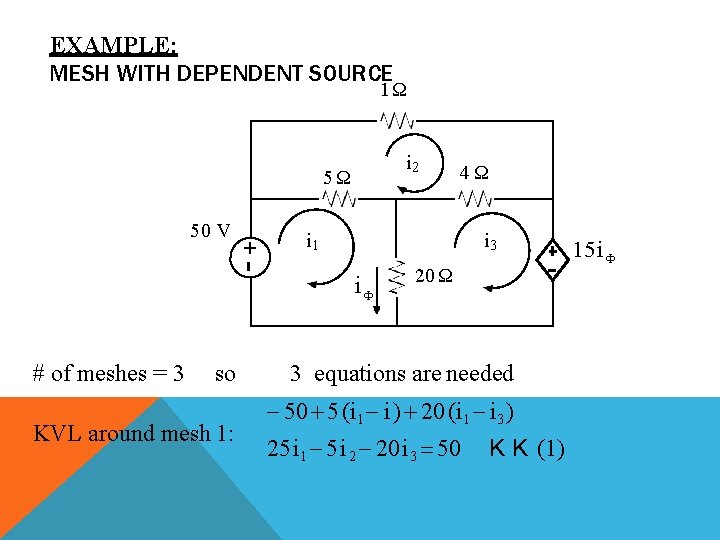
EXAMPLE: MESH WITH DEPENDENT SOURCE 1Ω i 2 5Ω +- 50 V i 1 i 3 iΦ # of meshes = 3 so KVL around mesh 1: 4Ω 20 Ω 3 equations are needed 50 5 (i 1 i ) 20 (i 1 i 3 ) 25 i 1 5 i 2 20 i 3 50 K K (1) 15 i Φ

KVL around mesh 2: 1 I 2 4 (I 2 I 3 ) 5 (I 2 I 1 ) 0 5 i 1 10 i 2 4 i 3 0 KVL around mesh 3: 15 i Φ 20 (i 3 i 1 ) 4 (i 3 i 2 ) 0 where K K (2) i Φ i 1 i 3 15 (i 1 i 3 ) 20 (i 3 i 1 ) 4 (i 3 i 2 ) 0 5 (i 1 i 3 ) 4 (i 3 i 2 ) 0 5 i 1 4 i 2 9 i 3 0 25 5 20 i 1 50 5 10 4 i 2 0 5 4 9 i 3 0 i 1 29. 6 A, i 2 26 A, i 3 28 A

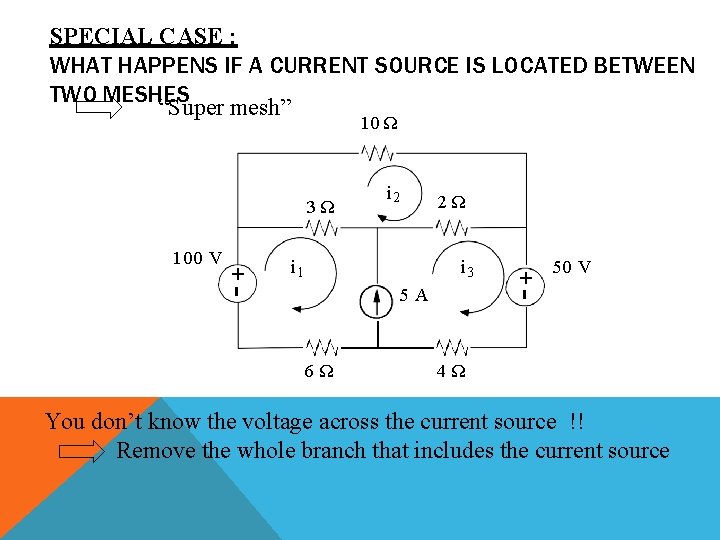
SPECIAL CASE : WHAT HAPPENS IF A CURRENT SOURCE IS LOCATED BETWEEN TWO MESHES “Super mesh” 10 Ω 3Ω 2Ω i 1 i 3 5 A 6Ω +- +- 100 V i 2 50 V 4Ω You don’t know the voltage across the current source !! Remove the whole branch that includes the current source

10 Ω 3Ω i 1 6Ω 2Ω i 3 +- +- 100 V i 2 50 V 4Ω Apply KVL around the super mesh 100 3(i 1 i 2 ) 2 (i 3 i 2 ) 50 4 i 3 6 i 1 0 9 i 1 5 i 2 6 i 3 50 KK(1)

KVL AROUND THE UPPER LOOP: 10 i 2 2 (i 2 i 3 ) 3(i 2 i 1 ) 0 3 i 1 15 i 2 2 i 3 0 K K (2) We also know i 3 i 1 5 A i 1 0 i 2 i 3 5 K K (3) i 1 1. 75 A i 2 1. 25 A i 3 6. 75 A

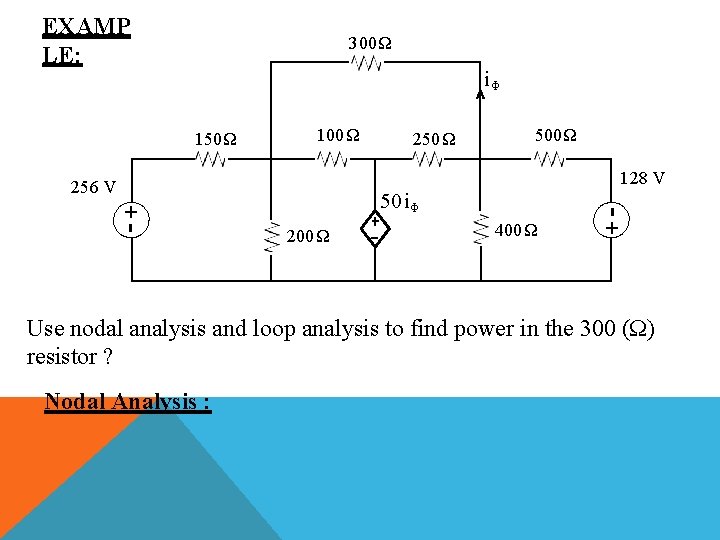
EXAMP LE: 300Ω iΦ 100 Ω 250 Ω 500 Ω 128 V 256 V +- 50 i Φ 200Ω 400Ω +- 150 Ω Use nodal analysis and loop analysis to find power in the 300 (Ω) resistor ? Nodal Analysis :

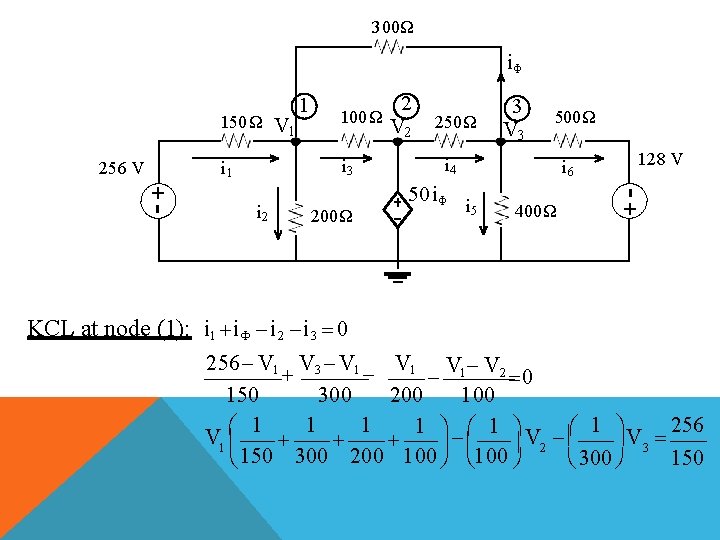
300Ω iΦ 256 V 100 Ω i 3 i 1 +- i 2 200Ω 2 V 2 250 Ω 3 V 3 500 Ω i 4 50 iΦ i 6 i 5 400Ω 128 V +- 150 Ω V 1 1 KCL at node (1): i 1 i Φ i 2 i 3 0 256 V 1 V 3 V 1 V 1 V 2 0 150 300 200 1 1 1 1 V 256 V 1 V 2 3 150 300 200 100 150 300

0. 0250 V 1 0. 01 V 2 0. 00333 V 3 1. 7067 KCL at node (3): K K (1) i 4 i 5 i 6 i Φ 0 V 2 V 3 V 3 128 V 3 V 1 0 150 400 500 300 V 1 V 2 1 1 1 128 1 V 3 300 250 400 500 300 500 0. 0033 V 1 0. 004 V 2 0. 0118 V 3 0. 256 K K (2) You can notice that V 2 50 i Φ V 3 V 1 1 1 V 2 50 V V 1 3 6 300 6 0. 166 V 1 1 V 2 0. 1667 V 3 0 K K (3)

0. 038 0. 01 0. 0033 V 1 1. 7067 3 0. 0033 0. 004 0. 0118 V 2 0. 256 1 0. 1667 V 3 0 0. 1667 V 1 62. 5 V V 2 11. 75 V V 3 8 V V 2 i Φ 0. 235 A 50 2 P 300Ω i Φ R 0. 235 2 300 16. 5675 W iΦ

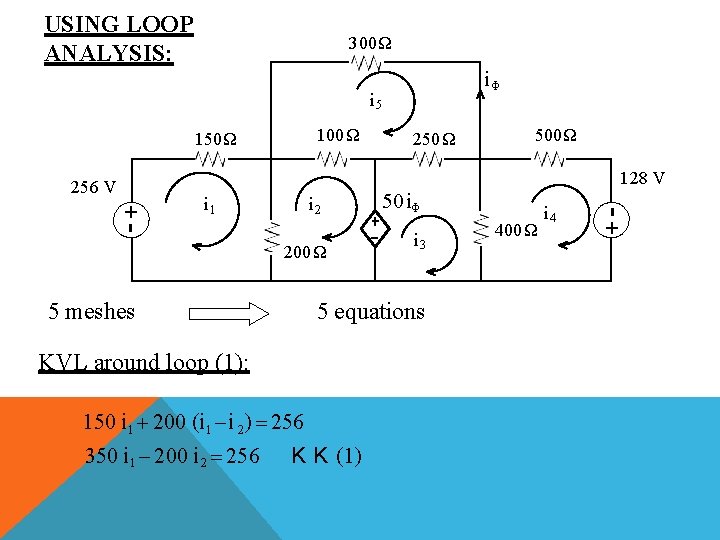
USING LOOP ANALYSIS: 300Ω iΦ i 5 100 Ω 150 Ω 500 Ω 128 V +- i 1 i 2 200Ω 5 meshes i 3 5 equations KVL around loop (1): 150 i 1 200 (i 1 i 2 ) 256 350 i 1 200 i 2 256 50 i Φ K K (1) 400Ω i 4 +- 256 V 250 Ω

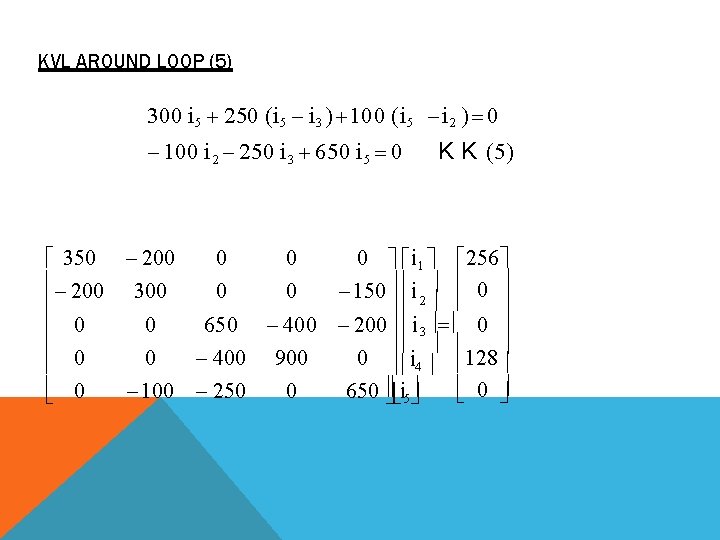
KVL AROUND LOOP (2): 100 (i 2 i 5 ) 50 i Φ 200 (i 2 i 1 ) 0 iΦ i 5 100 (i 2 i 5 ) 50 i 5 200 (i 2 i 1 ) 0 200 i 1 300 i 2 150 i 5 0 K K (2) KVL around loop (3) 500 i 4 128 400 (i 4 i 3 ) 0 400 i 3 900 i 4 128 K K (4) KVL around loop (4) 250 (i 3 i 5 ) 400 (i 3 i 4 ) 50 i Φ 0 650 i 3 400 i 4 200 i 5 0 since iΦ i 5 K K (3)

KVL AROUND LOOP (5) 300 i 5 250 (i 5 i 3 ) 100 (i 5 i 2 ) 0 100 i 2 250 i 3 650 i 5 0 K K (5) 0 0 0 i 1 256 350 200 i 0 200 300 0 0 150 2 0 0 650 400 200 i 3 0 400 900 0 i 4 128 0 0 0 100 250 0 650 i 5

I 1 1. 29 A i 2 0. 9775 A i 3 0. 22 A i 4 0. 24 A i 5 0. 235 A P 300Ω (i 5 ) 2 R (0. 235)2 (300) 16. 5675 W

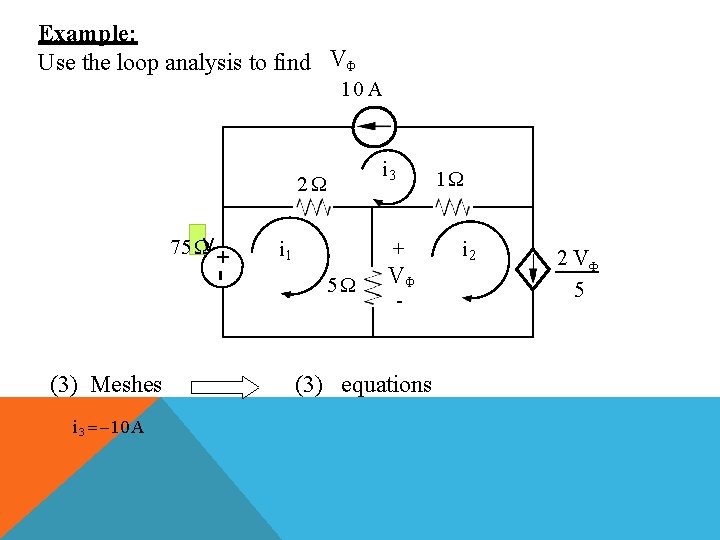
Example: Use the loop analysis to find VΦ 10 A 2Ω +- 75 ΩV (3) Meshes i 3 10 A i 1 i 3 + 5Ω VΦ - (3) equations 1Ω i 2 2 VΦ 5

KVL around loop (1): 2 (I 1 I 3 ) 5 (I 1 I 2 ) 75 0 7 i 1 5 i 2 20 75 0 7 i 1 5 i 2 55 K K (1) Equation of dependent source: 2 VΦ 5 V Φ 5 (i 1 i 2 ) i 2 2 i 2 5 i 1 i 2 2 i 1 2 i 5 K K (2) 2 i 1 3 i 2 0 2

7 5 I 1 55 2 3 i 0 2 i 1 15 A i 2 10 A VΦ 5 (i 1 i 2 ) 5 (15 10) 25 V VΦ 25 V
 Ministry of higher education afghanistan
Ministry of higher education afghanistan Kurdistan
Kurdistan Kurdistan
Kurdistan Kurdistan
Kurdistan Ministry of higher education saudi arabia
Ministry of higher education saudi arabia Face application
Face application Ministry of higher education tunisia
Ministry of higher education tunisia Ministry of higher education saudi arabia
Ministry of higher education saudi arabia Ministry of education and research romania
Ministry of education and research romania Ministry of education romania
Ministry of education romania Ministry of education and culture cyprus
Ministry of education and culture cyprus Hellenic ministry of education and religious affairs
Hellenic ministry of education and religious affairs Ministry of education and science of the russian federation
Ministry of education and science of the russian federation Ministry of education serbia
Ministry of education serbia What is textbook
What is textbook Matriculation certificate
Matriculation certificate Ministry of education armenia
Ministry of education armenia Ministry of education
Ministry of education Ministry of education iceland
Ministry of education iceland Ministry of national education morocco
Ministry of national education morocco Ministry of education
Ministry of education Ministry of education
Ministry of education Ministry of education peru
Ministry of education peru Ministry of education secondary engagement program
Ministry of education secondary engagement program Ministry of education
Ministry of education Ministry of education
Ministry of education Ministry of national education romania
Ministry of national education romania Ministry of education moldova
Ministry of education moldova Ministry of education zone 1
Ministry of education zone 1 Department of higher education and training
Department of higher education and training Havering college of further and higher education
Havering college of further and higher education Efficiency and effectiveness in higher education
Efficiency and effectiveness in higher education Demographics and the demand for higher education
Demographics and the demand for higher education Information gathered during an experiment
Information gathered during an experiment How is a scientific law different from a scientific theory?
How is a scientific law different from a scientific theory? Web analytics in higher education
Web analytics in higher education Capacity building in the field of higher education
Capacity building in the field of higher education Importance of faculty in higher education
Importance of faculty in higher education Ri board of governors
Ri board of governors Higher education ppc
Higher education ppc Massachusetts higher education consortium
Massachusetts higher education consortium Internationalization of higher education in the philippines
Internationalization of higher education in the philippines Higher education eprocurement
Higher education eprocurement Digital initiatives in higher education
Digital initiatives in higher education



































































