Mining Complex Data COMP 790 90 Seminar Spring

Mining Complex Data COMP 790 -90 Seminar Spring 2011 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Mining Complex Patterns § 2 Common Pattern Mining Tasks: § Itemsets (transactional, unordered data) § Sequences (temporal/positional: text, bioseqs) § Tree patterns (semi-structured/XML data, web mining) § Graph patterns (protein structure, web data, social network) COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

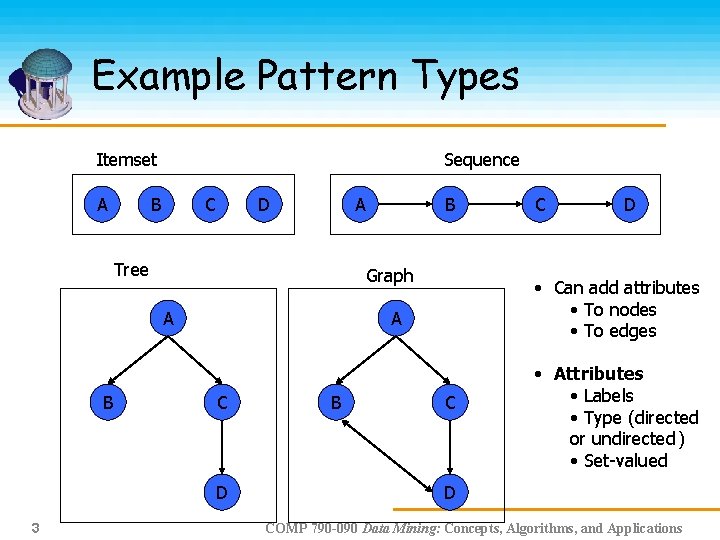
Example Pattern Types Itemset A Sequence B C D A Tree Graph A B C D • Can add attributes • To nodes • To edges A D 3 B C • Attributes • Labels • Type (directed or undirected ) • Set-valued D COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Induced vs Embedded Sub-trees Induced Sub-trees: S = (Vs, Es) is a sub-tree of T = (V, E) if and only if Vs ⊆ V e = (nx, ny) ∊ Es iff (nx, ny) ∊ E (nx directly connected to ny) Embedded Sub-trees: S = (Vs, Es) is a sub-tree of T = (V, E) if and only if Vs ⊆ V e = (nx, ny) ∊ Es iff nx ≤l ny in T (nx connected to ny) An induced sub-tree is a special case of embedded sub-tree. We say S occurs in T and T contains S if S is an embedded sub-tree of T If S has k nodes, we call it a k-sub-tree 4 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Mining Frequent Trees Support: the support of a subtree in a database of trees, is the number of trees containing the subtree. A subtree is frequent if its support is at least the minimum support. Tree. Miner: Given a database of trees (a forest) and a minimum support, find all frequent subtrees. 5 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

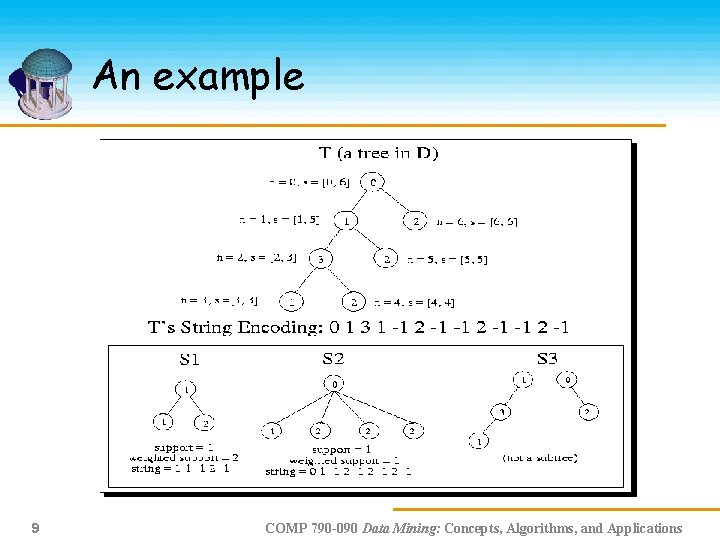
String Representation of Trees n 0 n 1 n 2 n 3 0 0 1 3 1 -1 2 -1 n 6 1 3 2 2 n 5 With N nodes, M branches, F max fanout Adjacency Matrix requires: N(F+1) space Adjacency List requires: 4 N-2 space 1 2 n 4 Tree requires (node, child, sibling): 3 N space String representation requires: 2 N-1 space 6 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Tree: String Representation Like an itemset -1 as the backtrack item Assuming only labels on nodes For trees labels on edges can be treated as labels on nodes: edge-label+node-label = new label! 7 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Match labels Subtree 0 Tree [0, 6] 0 0 n 0 [1, 5] 1 2 [3, 3] 8 3 2 n 5 1 2 n 3 n 4 1 2 2 2 n 6 n 1 [2, 4] [6, 6] 6 5 [5, 5] 4 [4, 4] 3 vector < id, match label, scope > Match Label: 03456 Support: 1 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

An example 9 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Generic Mining Algorithms Horizontal pattern matching based Vertical intersection based BFS or DFS 10 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Candidate Generation & Support Counting Candidate Generation Extend by a node or an edge Avoid duplicates as far as possible 11 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

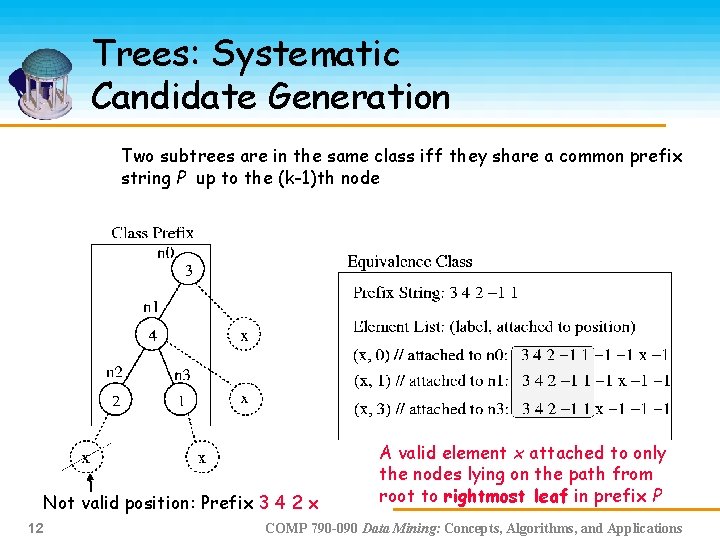
Trees: Systematic Candidate Generation Two subtrees are in the same class iff they share a common prefix string P up to the (k-1)th node Not valid position: Prefix 3 4 2 x 12 A valid element x attached to only the nodes lying on the path from root to rightmost leaf in prefix P COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Candidate generation Given an equivalence class of k-subtrees, how do we generate candidate (k+1)subtrees? Main idea: consider each ordered pair of elements in the class for extension, including self extension Sort elements by node label and position 13 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Class extension 14 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

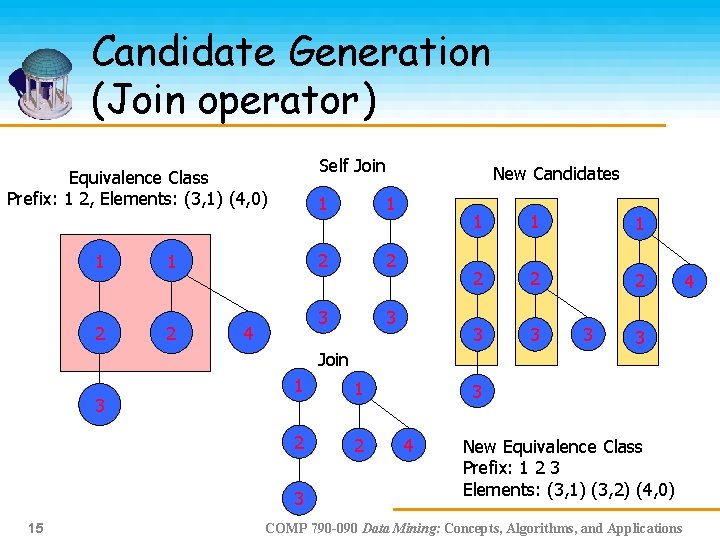
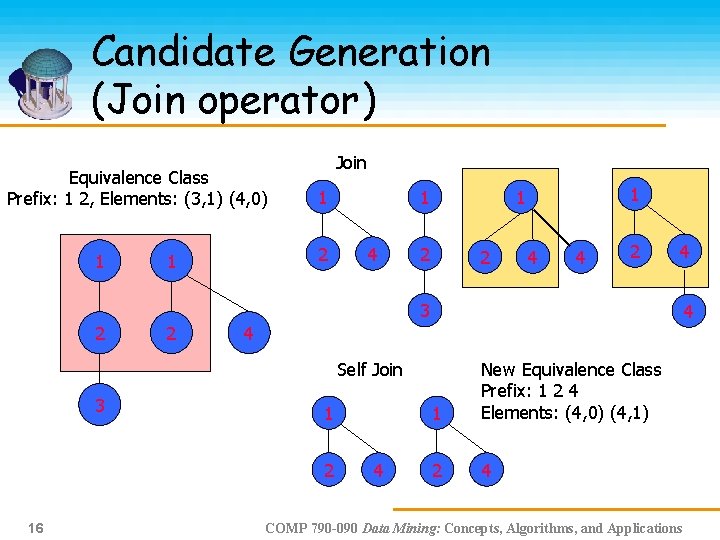
Candidate Generation (Join operator) Self Join Equivalence Class Prefix: 1 2, Elements: (3, 1) (4, 0) 1 2 4 1 1 2 2 3 3 New Candidates 1 1 1 2 2 2 3 3 Join 3 1 1 2 2 3 15 3 3 3 4 New Equivalence Class Prefix: 1 2 3 Elements: (3, 1) (3, 2) (4, 0) COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications 4

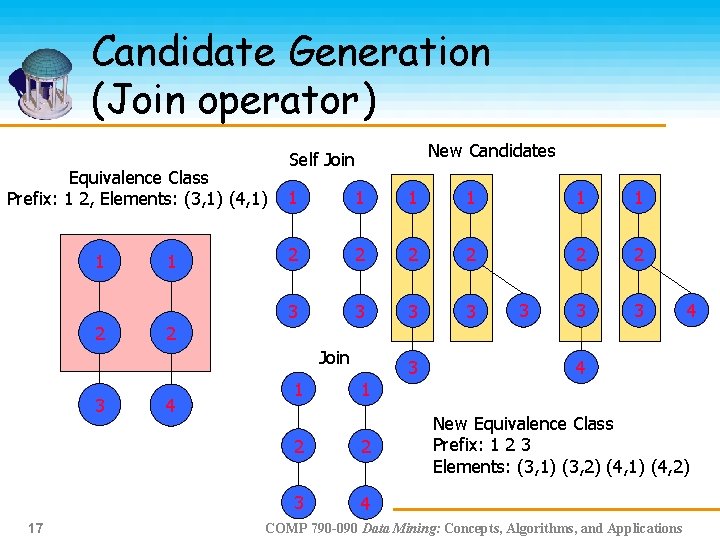
Candidate Generation (Join operator) Equivalence Class Prefix: 1 2, Elements: (3, 1) (4, 0) 1 Join 1 2 1 1 4 1 1 2 2 4 4 2 4 3 2 2 4 4 Self Join 3 1 2 16 4 1 New Equivalence Class Prefix: 1 2 4 Elements: (4, 0) (4, 1) 2 4 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

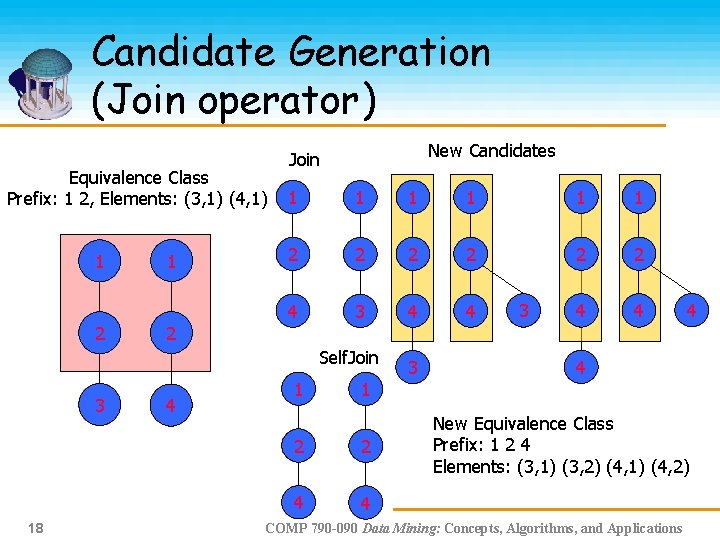
Candidate Generation (Join operator) Equivalence Class Prefix: 1 2, Elements: (3, 1) (4, 1) 1 2 1 New Candidates Self Join 1 1 1 2 2 2 3 3 3 17 4 2 Join 3 3 4 1 2 2 3 4 New Equivalence Class Prefix: 1 2 3 Elements: (3, 1) (3, 2) (4, 1) (4, 2) COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Candidate Generation (Join operator) Equivalence Class Prefix: 1 2, Elements: (3, 1) (4, 1) 1 2 1 New Candidates Join 1 1 1 2 2 2 4 3 4 4 18 4 2 Self. Join 3 3 4 1 2 2 4 4 New Equivalence Class Prefix: 1 2 4 Elements: (3, 1) (3, 2) (4, 1) (4, 2) COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications

Apriori Style Tree. Miner 19 COMP 790 -090 Data Mining: Concepts, Algorithms, and Applications