Minimum weight design by GENOPTBIGBOSOR 4 of an

Minimum weight design by GENOPT/BIGBOSOR 4 of an externally pressurized circumferentially corrugated cylindrical shell and verification by STAGS David Bushnell, retired 775 Northampton Drive, Palo Alto, CA 94303 bush@sonic. net January 2015

Summary • • • What is GENOPT? What is BIGBOSOR 4? Geometry, decision variables Behaviors that constrain the design during optimization cycles The objective: WEIGHT Optimization via SUPEROPT “Smoothing” segments Nonlinear axisymmetric pre-buckling behavior Local bifurcation buckling from BIGBOSOR 4 and STAGS General bifurcation buckling from BIGBOSOR 4 and STAGS Extreme sensitivity of an optimized design to perturbations Conclusions

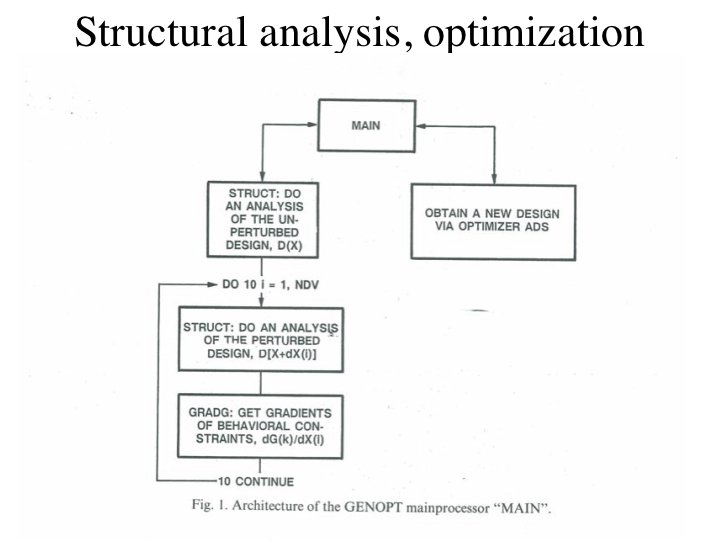
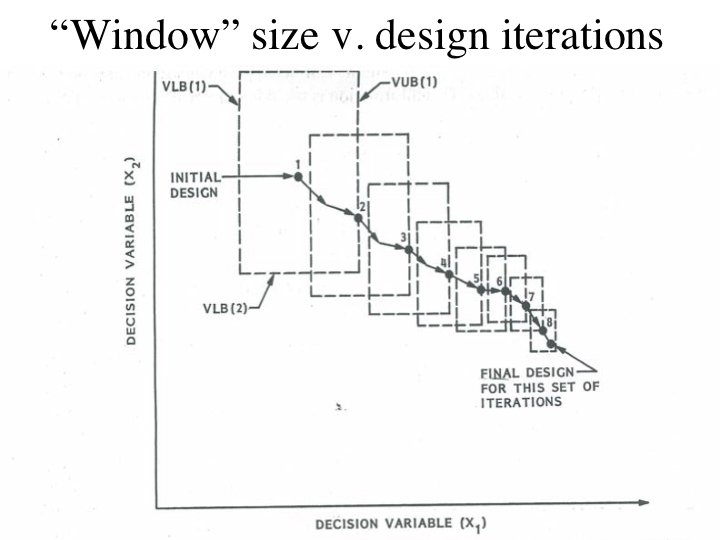
GENOPT is used in combination with BIGBOSOR 4. Optimization is performed with GENOPT/BIGBOSOR 4/ADS. The optimizer is ADS, a gradientbased optimizer written by Vanderplaats and his colleagues in the 1980 s

What is BIGBOSOR 4? • Stress, buckling and vibration of elastic shells of revolution (BIGBOSOR 4=BOSOR 4 with more shell segments permitted, up to 295 shell segments as of 2011). • Nonlinear axisymmetric stress analysis • Linear non-axisymmetric stress analysis • Axisymmetric or non-axisymmetric bifurcation buckling • Linear vibration modes of axisymmetrically loaded shell • Multi-segment, branched, ring-stiffened shells of revolution • Various wall constructions • BIGBOSOR 4 cannot handle local shell segment transverse shear deformation (t. s. d. ) or local shell wall anisotropy or bifurcation buckling with applied in-plane shear loading. Use a factor of safety to compensate for these effects on local buckling.

Last year’s paper: longitudinally corrugated prismatic panels

This year’s paper: circumferentially corrugated shells

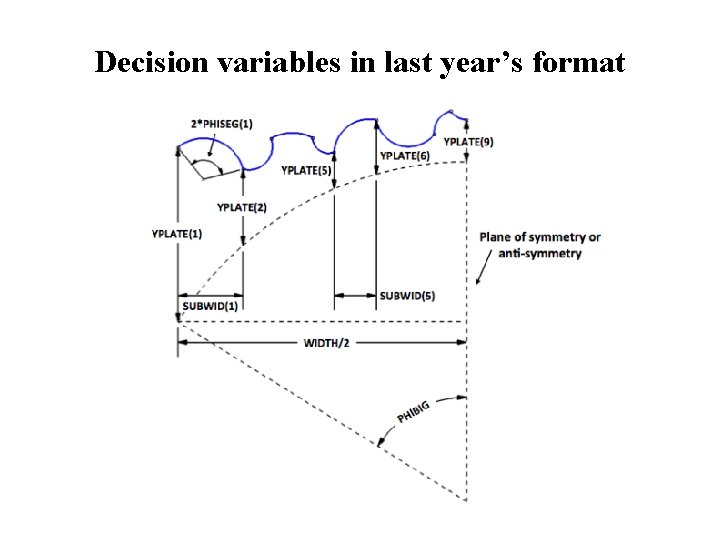
Decision variables in last year’s format

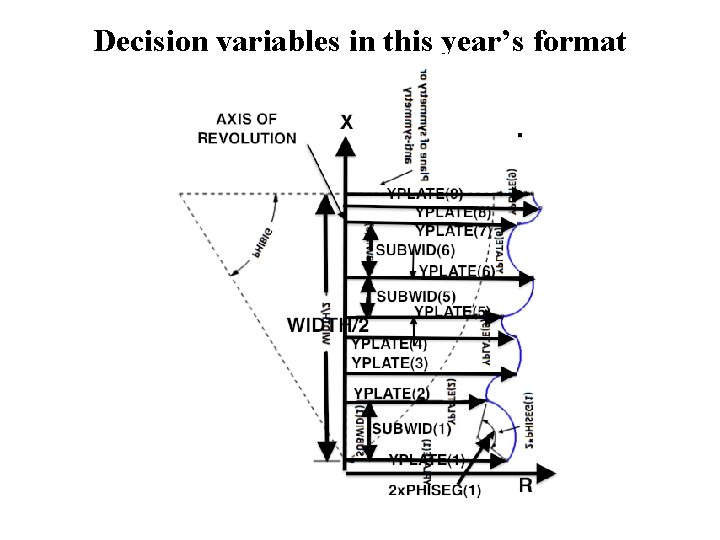
Decision variables in this year’s format

The circumferentially corrugated shell of revolution is optimized subject to the following “behavioral” constraints: • Local buckling that is symmetric about the symmetry plane at X = WIDTH/2 • General buckling that is symmetric about the symmetry plane at X = WIDTH/2. • General buckling that is anti-symmetric about the symmetry plane at X = WIDTH/2. • Maximum allowable stress

The objective is: • Objective= WEIGHT (lb) of the entire panel of WIDTH = X inches

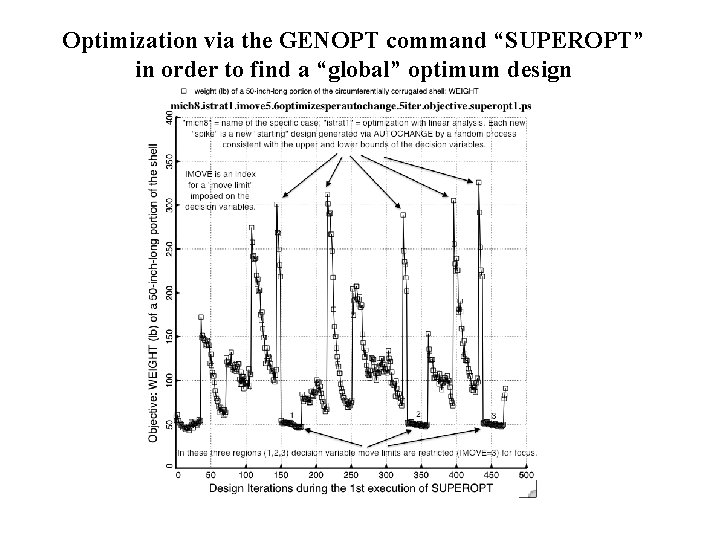
Optimization via the GENOPT command “SUPEROPT” in order to find a “global” optimum design

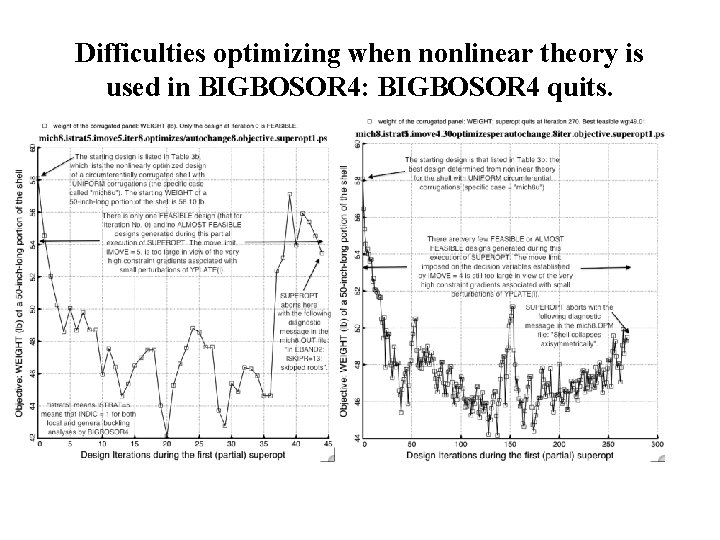
Difficulties optimizing when nonlinear theory is used in BIGBOSOR 4: BIGBOSOR 4 quits.

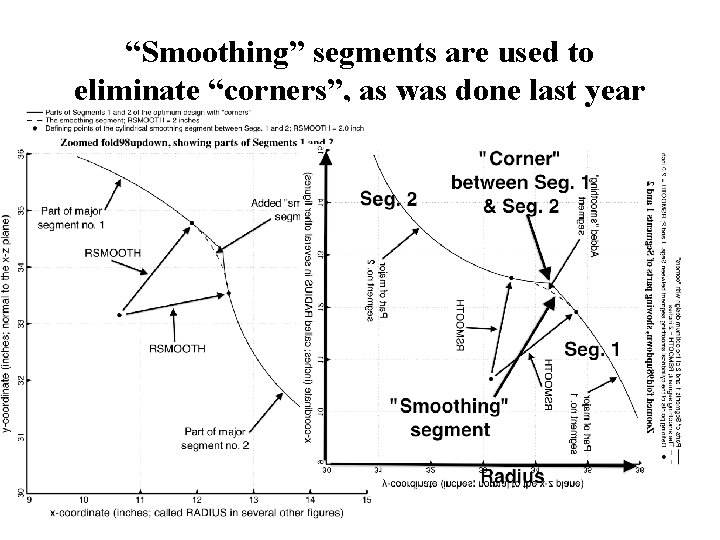
“Smoothing” segments are used to eliminate “corners”, as was done last year

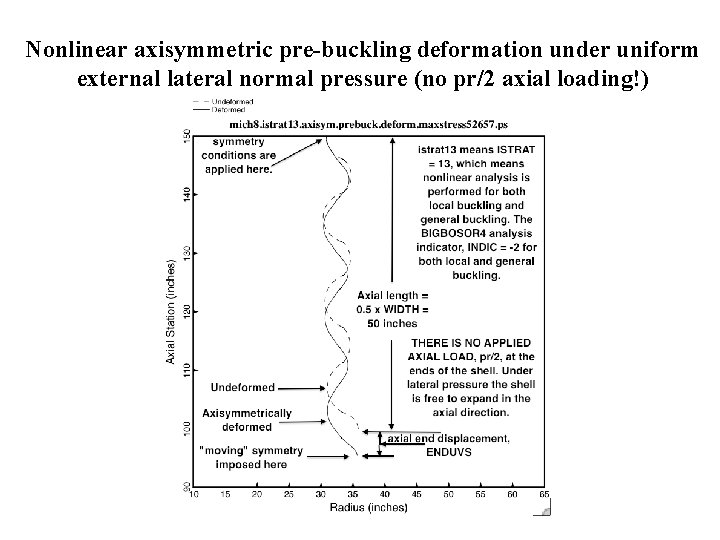
Nonlinear axisymmetric pre-buckling deformation under uniform external lateral normal pressure (no pr/2 axial loading!)

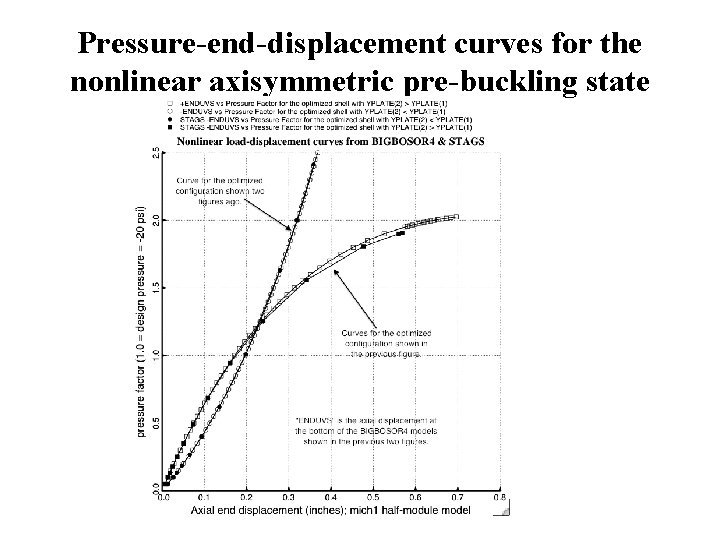
Pressure-end-displacement curves for the nonlinear axisymmetric pre-buckling state

Nonlinear local buckling from the BIGBOSOR 4 model of the nonlinearly optimized “mich 8” configuration

Nonlinear local buckling from the STAGS model of the nonlinearly optimized “mich 8” configuration

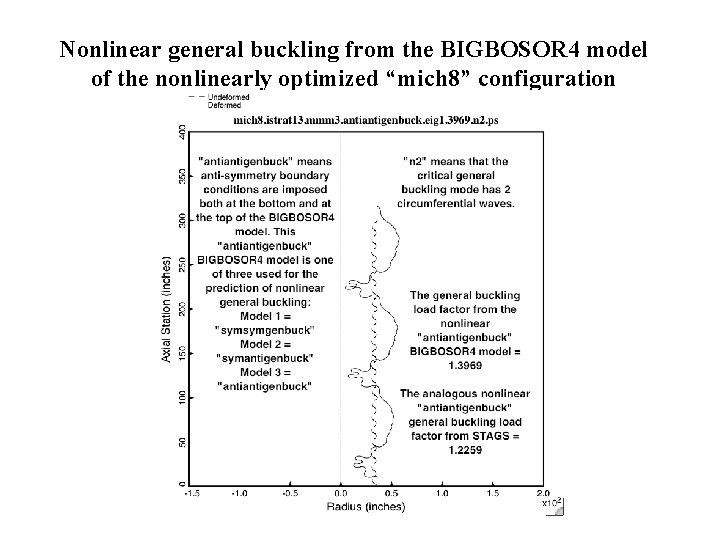
Nonlinear general buckling from the BIGBOSOR 4 model of the nonlinearly optimized “mich 8” configuration

Nonlinear general buckling from the STAGS model of the nonlinearly optimized “mich 8” configuration

Comparison of predictions from BIGBOSOR 4 and STAGS for linearly and nonlinearly optimized “mich 8” configurations

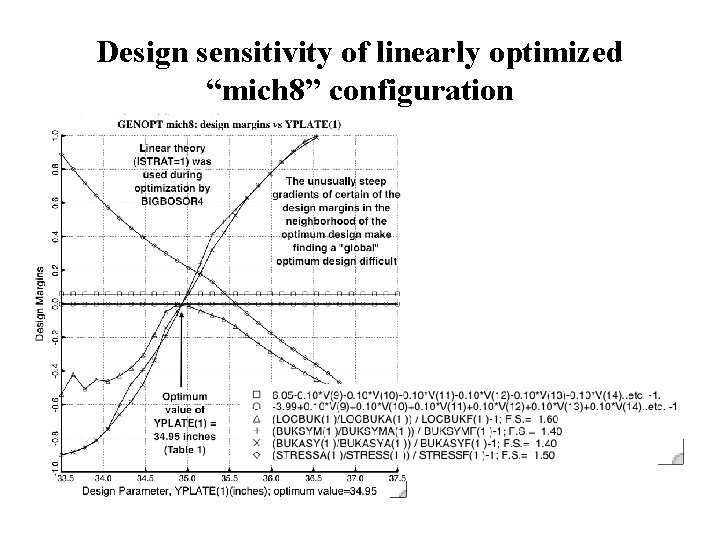
Design sensitivity of linearly optimized “mich 8” configuration

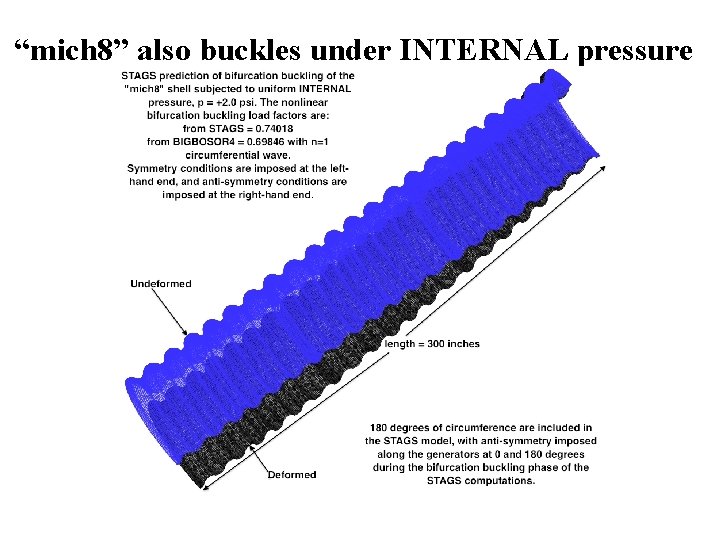
“mich 8” also buckles under INTERNAL pressure

Conclusions • “Global” optimum designs are difficult to find because of extreme design sensitivity and because of certain difficulties with nonlinear bifurcation buckling calculations in connection with optimization. • BIGBOSOR 4 and STAGS predictions agree very well for linearly optimized configurations. • BIGBOSOR 4 and STAGS predictions differ somewhat for nonlinearly optimized configurations. • Nonlinear effects are significant for optimized designs in the cases treated here.