MINIMUM TRUE AND MAXIMUM FALSE VERTICES METHOD FOR








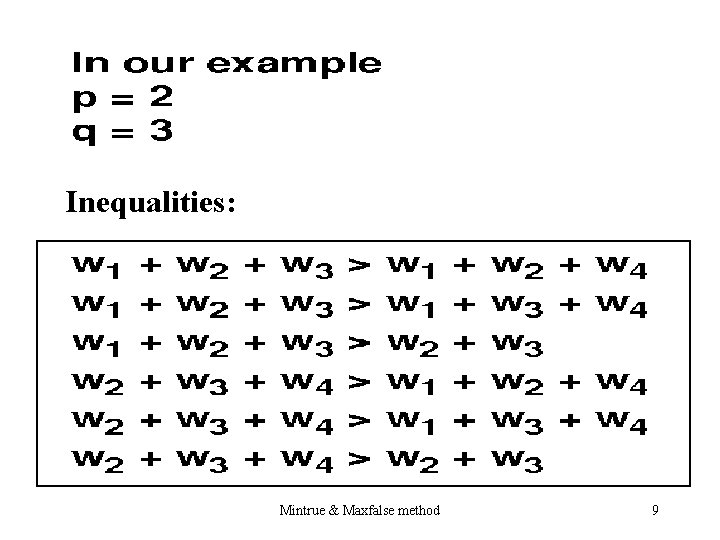


















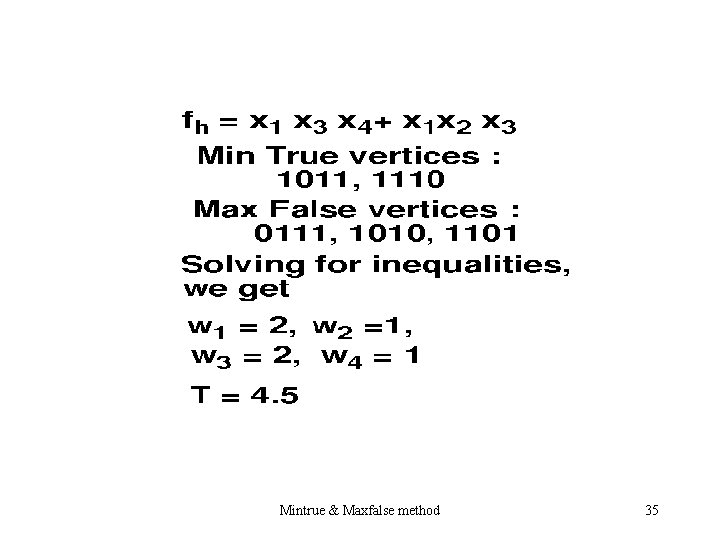

- Slides: 37

MINIMUM TRUE AND MAXIMUM FALSE VERTICES METHOD FOR REALIZATION OF THRESHOLD GATES Mintrue & Maxfalse method 1

Comparing bit by bit and determining which is greater Mintrue & Maxfalse method 2

Steps involved in finding Minimum True and Maximum False vertices • • Determine the positive function Determine Minimum True vertices Anything greater than these are True Vertices Remaining are all False Vertices Determine maximal false vertices Anything less than false are neglected or crossed Others which are not compared are false For false we start from bottom to top Mintrue & Maxfalse method 3

Example: Finding Minimum True vertices Mintrue & Maxfalse method 4

Example 1: Find the weights and threshold for the following fn. Step 1: Determine the Positive Function Step 2: Find all Minumum True and Maximum false vertices Mintrue & Maxfalse method 5

Determining the Mintrue and Maxfalse vertices Mintrue & Maxfalse method 6

Mintrue & Maxfalse method 7

Step 3: p = Number of Minimum True Vertices q = Number of Maximum false Vertices Mintrue & Maxfalse method 8
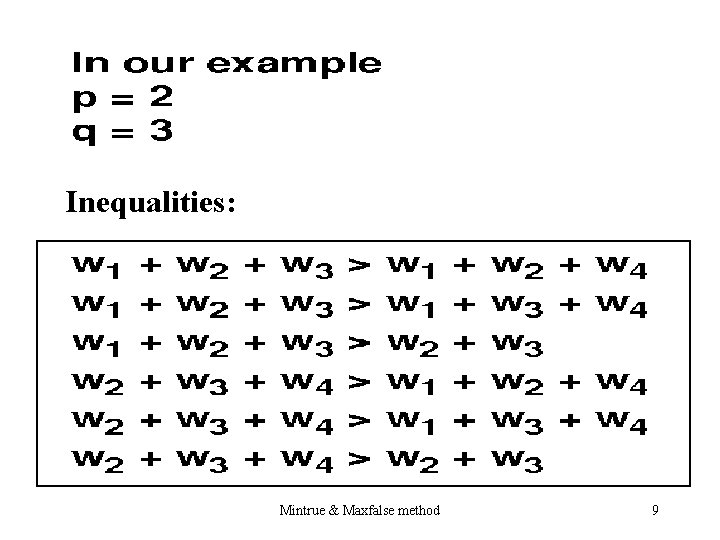
Inequalities: Mintrue & Maxfalse method 9

Solving the inequalities: Substituting the weights in Min True vertices: Mintrue & Maxfalse method 10

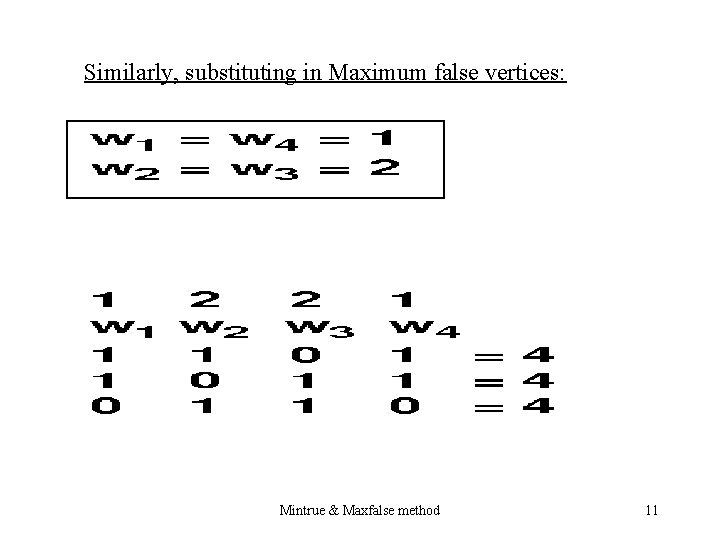
Similarly, substituting in Maximum false vertices: Mintrue & Maxfalse method 11

The Threshold T must be smaller than 5 but larger than 4. (Min Limit < Threshold < Max Limit) Hence T = 4. 5 Mintrue & Maxfalse method 12

In the example, the inputs X 3 and X 4 appear in f in complimented form, hence the new weighted vectors are given by: * Complimenting the weights of X 3 and X 4 * Subtracting the Threshold obtained by the weights of these two inputs Ans: Mintrue & Maxfalse method 13

Example 2: Find the Threshold and Weights of the following fn. Mintrue & Maxfalse method 14

Mintrue & Maxfalse method 15

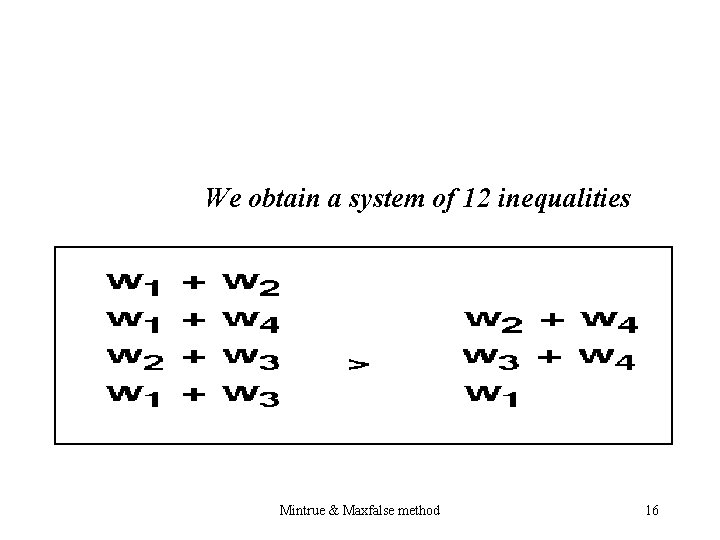
We obtain a system of 12 inequalities Mintrue & Maxfalse method 16

These impose several constraints on the weights associatedwith the function f. Mintrue & Maxfalse method 17

Mintrue & Maxfalse method 18

Mintrue & Maxfalse method 19

T must be smaller than 4 but larger than 3. Weight Threshold vector is given by: (3, 2, 2, 1; 3. 5) To find the corresponding vector for the original function, X 1 and X 3 must be complimented Mintrue & Maxfalse method 20

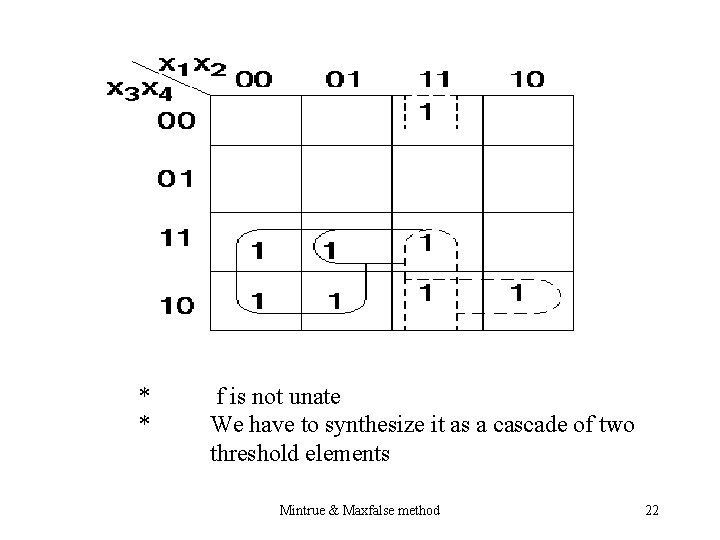
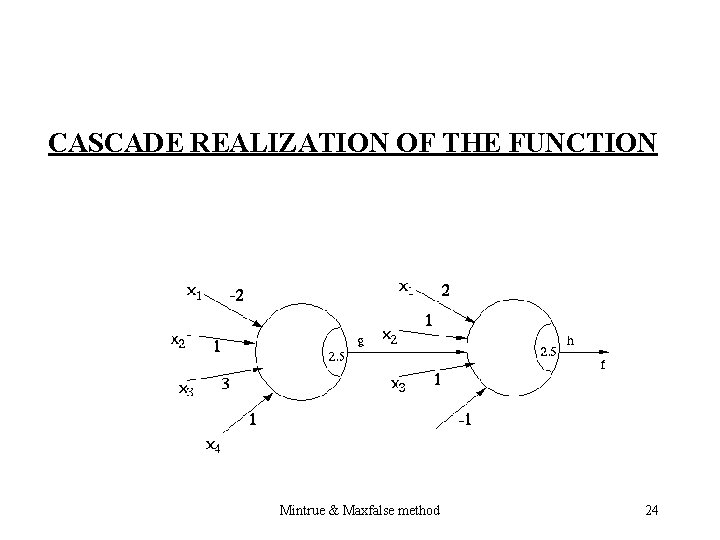
Example 1: Mintrue & Maxfalse method 21

* * f is not unate We have to synthesize it as a cascade of two threshold elements Mintrue & Maxfalse method 22

g(X 1, X 2, X 3, X 4) = {2, 3, 6, 7, 15} The weight-threshold vector for the function g is Vg = (-2, 1, 3, 1 ; 2. 5) h(X 1, X 2, X 3, X 4) = {10, 12, 14, 15} The weight-threshold vector for the function h is Vh = (2, 1, 1, -1 ; 2. 5) Mintrue & Maxfalse method 23

CASCADE REALIZATION OF THE FUNCTION Mintrue & Maxfalse method 24

* * f must have a value 1 whenever g does, the minimum weighted sum must be larger than the threshold of the second element. Negative values affect the most Mintrue & Maxfalse method 25

Calculating Wg Wg + 0 > 5/2 is the vital case Wg > 5/2 Wg = 3 This is the minimum weighted sum. So Wg is calculated from this. As a general rule, the weight of Wg should be the sum of the threshold of second element and the absolute value of all negative weights of the second element Mintrue & Maxfalse method 26

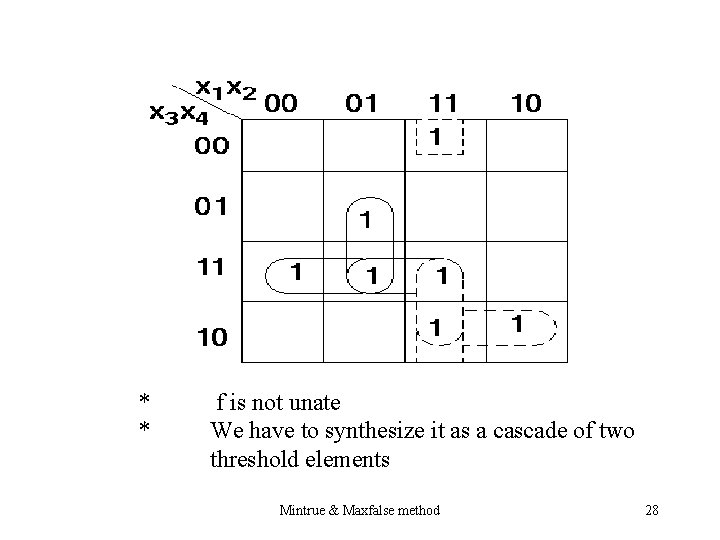
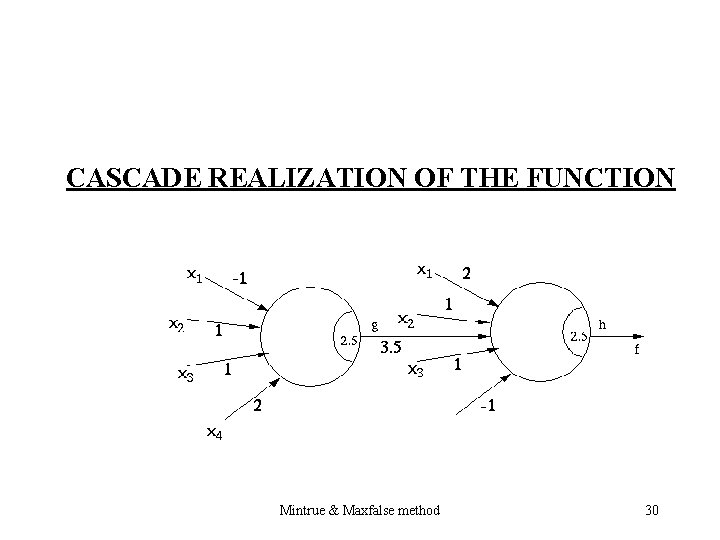
Example 2: Mintrue & Maxfalse method 27

* * f is not unate We have to synthesize it as a cascade of two threshold elements Mintrue & Maxfalse method 28

g(X 1, X 2, X 3, X 4) = {3, 5, 7, 15} The weight-threshold vector for the function g is Vg = (-1, 1, 1, 2 ; 2. 5) h(X 1, X 2, X 3, X 4) = {10, 12, 14, 15} The weight-threshold vector for the function h is Vh = (2, 1, 1, -1 ; 2. 5) Mintrue & Maxfalse method 29

CASCADE REALIZATION OF THE FUNCTION Mintrue & Maxfalse method 30

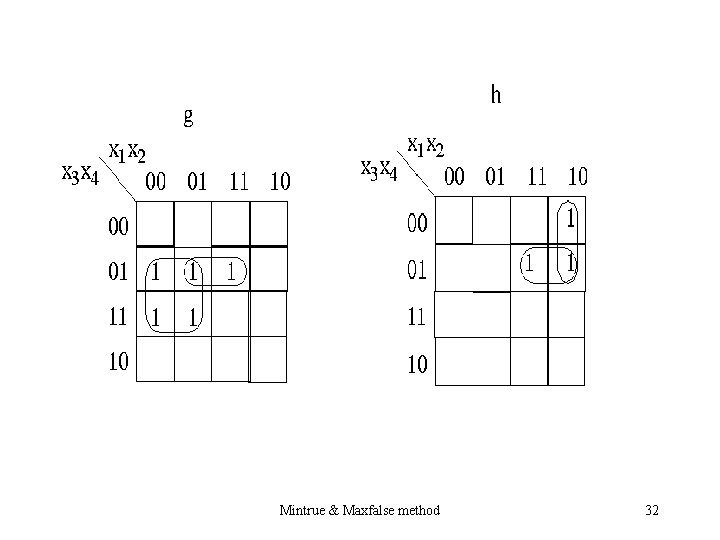
Example 3: f(X 1, X 2, X 3, X 4 ) = (2, 3, 6, 7, 8, 9, 13, 15) Realize this as a cascade of two functions Mintrue & Maxfalse method 31

Mintrue & Maxfalse method 32

Mintrue & Maxfalse method 33

Solving the inequalities, we get the weights as: Mintrue & Maxfalse method 34
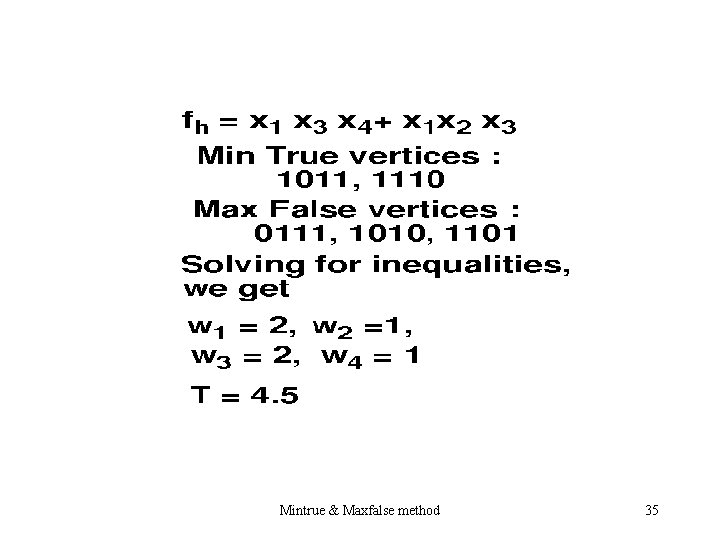
Mintrue & Maxfalse method 35

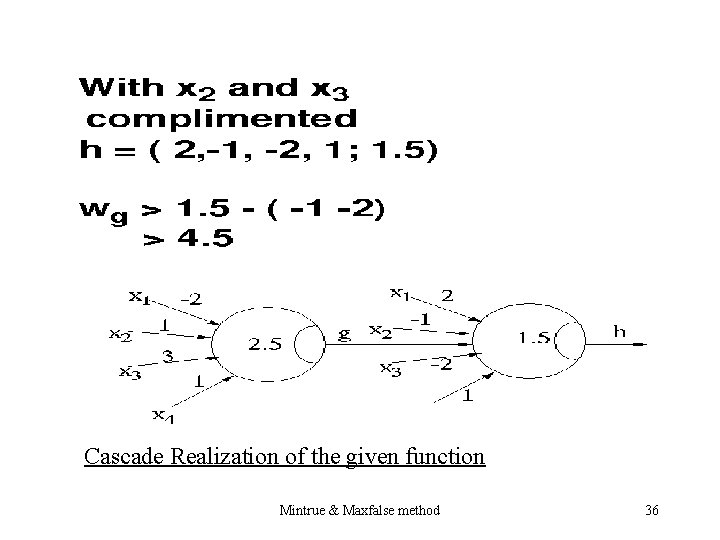
Cascade Realization of the given function Mintrue & Maxfalse method 36

questions? ? ? Mintrue & Maxfalse method 37